3.5 ПОЛ/ПОТОЛОК: СУММЫ

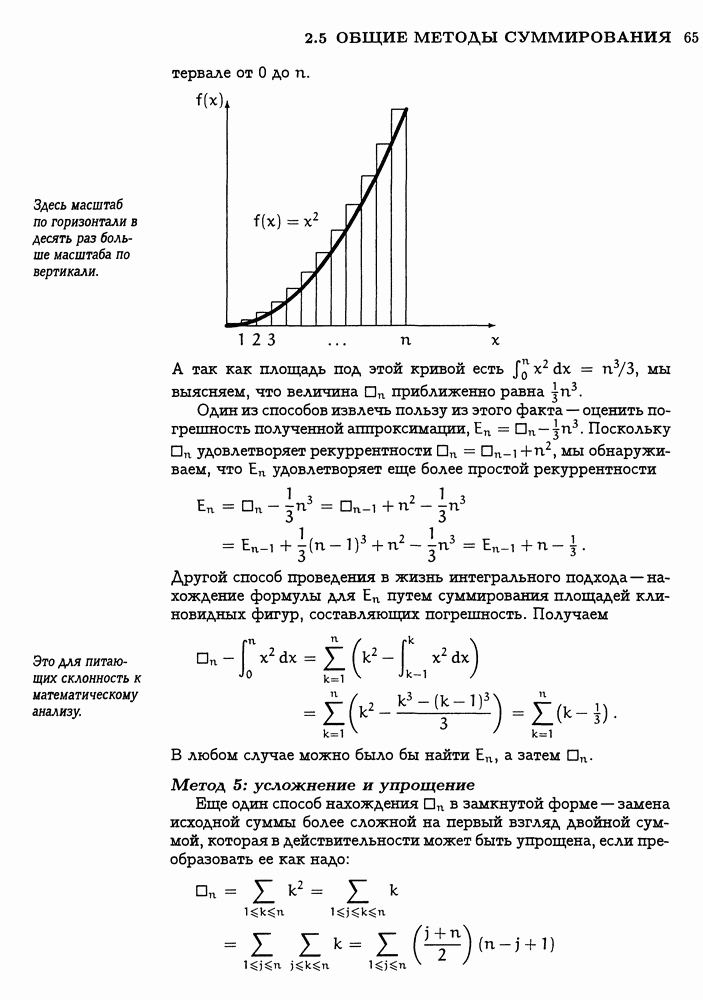
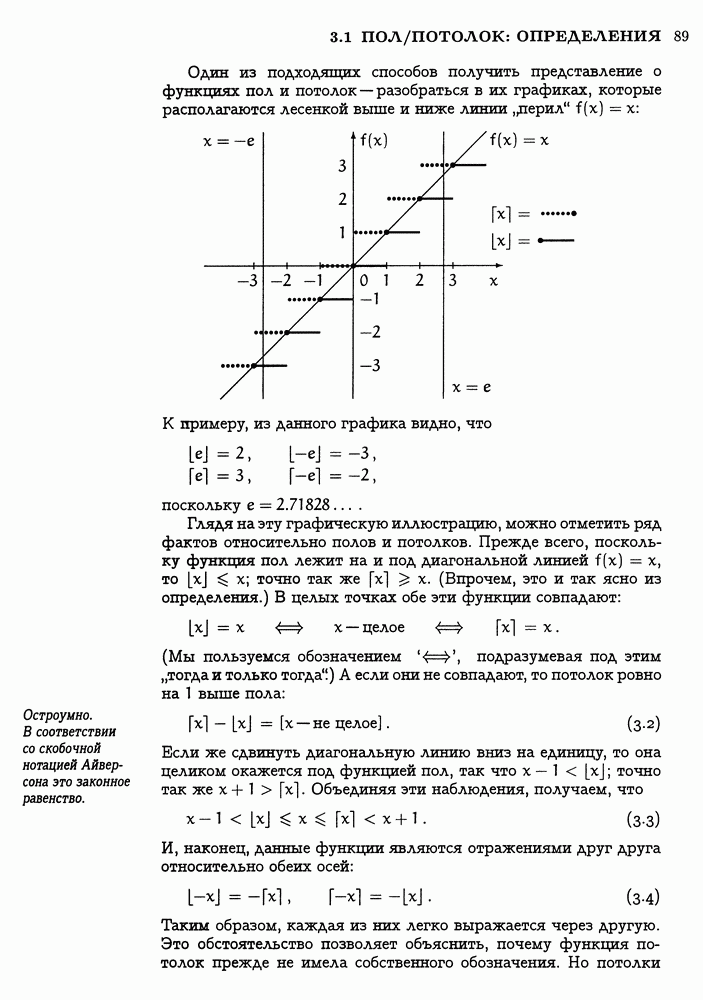
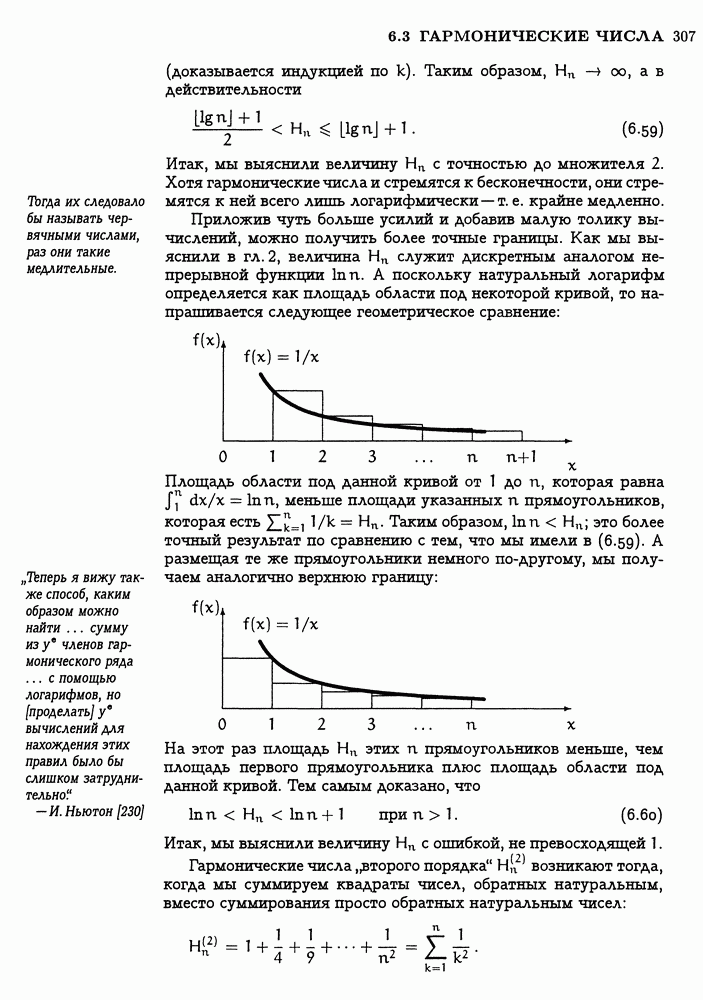
Уравнение (3.26) наглядно показывает, что по крайней мере один вид сумм, включающих в себя скобки можно получить в замкнутой форме. А есть ли другие? Есть. Уловка, которая обычно срабатывает в таких случаях, заключается в том, чтобы избавиться от пола или потолка, введя новую переменную.

Посмотрим, к примеру, можно ли получить сумму

в замкнутой форме. Предлагается ввести переменную это можно сделать „чисто механически действуя так же, как в задаче с рулеткой:

И вновь некоторые затруднения с граничными условиями. Допустим сначала, что — точный квадрат. Тогда вторая сумма обращается в нуль, а первая может быть вычислена по обычному правилу:

В общем случае можно положить тогда нужно всего лишь сложить члены при причем все они равны а, так что в сумме дают А это дает сумму в требуемой замкнутой форме:

Другой подход к вычислению подобных сумм состоит в замене выражения вида на что допустимо всегда, когда

. Вот как выглядит этот подход в случае суммы [квадратных корней], если для удобства предположить, что

А вот другой пример, в котором замена переменной приводит к преобразованной сумме. В 1909 г. независимо друг от друга и практически одновременно три математика — Боль [30], Серпински [269] и Вейль [49] — обнаружили замечательный факт: если число а иррационально, то при дробные доли распределены весьма равномерно между 0 и 1. Одна из формулировок этого факта такова:

при любом иррациональном а и любой ограниченной функции которая непрерывна почти всюду. В частности, полагая можно найти среднее значение которое оказывается равным (Именно этого и следовало ожидать, но разве не приятно сознавать, что это справедливо вне зависимости от того, каково на самом деле иррациональное число а.)

Теорема Боля, Серпинского и Вейля доказывается путем аппроксимации сверху и снизу „ступенчатыми функциями, которые являются линейными комбинациями простых функций

при Однако наша цель состоит не в доказательстве этой теоремы — это удел книг по численным методам. Мы же попробуем выяснить основную причину, по которой она справедлива, рассмотрев частный случай Другими словами, попробуем выяснить, насколько близка сумма

к идеальному значению если велико и а иррационально.

С этой целью определим отклонение как максимум по всем абсолютной величины суммы

Наша задача — показать, что не «слишком велико» по сравнению с показав, что величина всегда достаточно мала для иррационального

Сначала можно переписать в более простом виде, а затем ввести новый индекс суммирования у.

Если нам повезет, то можно будет просуммировать по к. Но прежде стоит ввести некоторые новые переменные, чтобы привести эту формулу в божеский вид. Не умаляя общности, предположим, что и положим:

Таким образом, — это дробная часть — это -дробная часть от

И вновь единственное, что нас огорчает, - это граничные условия. Поэтому давайте пока забудем про ограничение и вычислим сумму по к без него:

Ну, а дальше совсем просто — подставляем это выставляем

где — поправка на случаи к от которых нам не удалось избавиться. Величина а будет целой только при поскольку число а (и, следовательно, а) иррационально, а величина будет целой самое большее при одном значении Так что можно „спуститься с потолка на пол“:

Интересно — вместо суммы в замкнутой форме мы получаем сумму, которая весьма похожа на но отличается параметрами: вместо вместо и вместо . А что если получить

рекуррентность для которая (как мы надеемся) приведет к рекуррентности для отклонения Это означает, что мы хотим ввести в рассмотрение сумму

получая рекуррентность

Вспоминая, что мы обнаруживаем, что все прекрасно упростится, если заменить на

Здесь — некоторая положительная добавка, меньшая . В упр. 18 доказывается, что подобно ей лежит между . К тому же можно вывести из суммы член при так как он дает либо либо Следовательно, если взять максимум абсолютных величин по всем то получим

Методы, которые мы будем изучать в последующих главах, позволяют, исходя из этой рекуррентности, сделать вывод о том, что всегда много меньше если достаточно велико. Следовательно, теорема (3.28) справедлива; однако сходимость к пределу не всегда очень быстрая (см. упр. 9.45 и 9.61).

Вот-те на — всего лишь упражнение на манипуляции с суммами, полами и потолками. Читателям, которые не приучены „доказывать, что погрешности невелики; трудно поверить в то, что у кого-то могло бы хватить смелости не отступить перед такими безнадежными суммами. На самом деле повторное рассмотрение показывает, что все это вычисление пронизывает одна простая мысль. Суть ее в том, что некоторая сумма из членов может быть сведена к аналогичной сумме из не более чем членов. Все остальное сводится на нет, за исключением небольшого остатка, образованного из близких к граничным членов.

А теперь вдохнем поглубже и вычислим еще одну сумму, которая также нетривиальна, но имеет одно огромное преимущество (по сравнению с только что вычисленной): она выражается в замкнутой форме, так что можно легко проверить ответ. Теперь задача будет состоять в том, чтобы обобщить сумму в (3.26), найдя выражение для

Нахождение этой суммы в замкнутой форме — орешек покрепче тех, с которыми мы имели дело до сих пор (за исключением,

возможно, задачи об отклонении, с которой мы только что разобрались). Но эта задача настолько поучительна, что мы будем возиться с ней до самого конца данной главы.

Как обычно, особенно при решении трудных задач, начнем с рассмотрения простых крайних случаев. Частный случай — это тождество (3.26), в котором х заменено на

И как в гл. 1 имеет смысл получить еще некоторую информацию, снизойдя до случая

Но в нашей задаче два параметра, тип; теперь посмотрим, как выглядят некоторые частные случаи для . Если то в сумме всего один член, равный Если же то сумма равна Можно избавиться от взаимодействия если вынести за знак функции пол, но чтобы сделать это, надо рассмотреть отдельно случаи четного и нечетного Если — четное, то — целое число, так что его можно вынести за знак пола:

Если же — нечетное, то — целое число, так что мы получаем

Последний шаг следует из (3.26) при

Эти формулы при четном и нечетном несколько напоминают формулы при и 1, но отчетливой закономерности пока еще не просматривается, так что лучше продолжить рассмотрение еще нескольких крайних случаев. При сумма равна

и возможны три варианта для либо оно кратно 3, либо на 1 или на 2 больше этого кратного — т. е. или 2. Если то — целые числа, так что сумма равна

Если то — целые числа, так что имеем

Здесь последний шаг опять следует из (3.26), на этот раз при . И, наконец, если то

Наши левые мозговые полушария уже разобрались со случаем но правые все еще никак не могут последовать их примеру, поэтому перейдем к случаю

По крайней мере теперь мы знаем уже достаточно, для того чтобы рассмотреть случаи, основанные на значении Если то

А если , то

Случай как выясняется, дает тот же самый ответ. Наконец, в случае мы получаем нечто несколько иное, и это нечто оказывается важным ключом к установлению закономерности в общем случае:

На последнем шаге упрощается нечто вида что вновь оказывается частным случаем (3.26).

Вот сводка значений нашей суммы при малых

Это выглядит так, как если бы мы имели нечто вида , где каким-то образом зависят от Даже близорукие в состоянии заметить, что похоже, равно Труднее разглядеть выражение для а, но случай указывает на то, что а, похоже, равно — наибольшему общему делителю тип. Это не лишено смысла, так как — это тот множитель, который мы выделяем из приводя дробь к несократимой, а наша сумма включает в себя дробь . (Операции с будут обстоятельно рассмотрены в гл. 4.) Величина с представляется более таинственной, но, возможно, она как-нибудь получится в ходе доказательства наших предположений относительно а и

Вычисляя сумму при малых мы, по существу, переписали каждый член этой суммы в виде

ибо — целое число, которое может быть вынесено за скобки пола. Таким образом, исходную сумму можно представить в следующем развернутом виде:

Когда мы экспериментировали с малыми значениями эти три колонки приводили нас соответственно к .

В частности, теперь можно понять, откуда берется Вторая колонка представляет собой арифметическую прогрессию, сумма которой нам известна — это среднее первого и последнего членов, помноженное на число членов:

Таким образом, наша догадка, что подтвердилась.

Первая и третья колонки стоят покрепче: чтобы определить а и с, надо повнимательнее присмотреться к последовательности чисел

Допустим, к примеру, что Если представить эту последовательность в виде часового циферблата, то данные числа суть 0 часов (12 часов принимается за 0 часов), затем 5 часов, 10 часов, 3 часа ( часов), 8 часов и т. д. — оказывается, что каждый час пробивает лишь однажды.

Предположим теперь, что . Тогда данные числа суть 0 часов, 8 часов, 4 часа часов), но затем 0, 8 и 4 повторяются. Так как 8 и 12 кратны 4, а числа начинаются с 0 (тоже кратного 4), вырваться из этого замкнутого круга невозможно — все числа должны быть кратны 4.

В этих двух случаях мы имеем Общее правило, которое будет доказано в следующей главе, гласит, что если то мы получаем последовательность чисел взятых в некотором порядке, за которой следуют еще копий той же последовательности. К примеру, при набор чисел 0, 8, 4 встречается четыре раза.

Итак, первая колонка суммы приобретает ясный смысл: она содержит копий членов взятых в некотором порядке, так что их сумма равна

Здесь последний шаг — еще одно применение (3.26). Наша догадка относительно а подтвердилась:

А теперь, как мы и предполагали, можно вычислить с, ибо становится понятным содержание третьей колонки. Она содержит копий членов арифметической прогрессии так что сумма их равна

на самом деле элементы третьей колонки не складываются, а вычитаются, так что

Конец загадкам, конец догадкам. Искомая сумма в замкнутой форме выглядит так:

где . В порядке проверки можно убедиться в том, что это проходит для уже известных нам частных случаев Если то получаем в этой формуле два последних члена равны нулю, поэтому формула дает правильный ответ . А при мы получаем два последних члена чудесно сокращаются и сумма равна просто

После небольшой манипуляции с полученным замкнутым выражением его можно сделать даже симметричным относительно тип:

Это несколько неожиданно, поскольку нет никакого повода подозревать, что такая сумма должна быть симметричной. Нами доказан „закон взаимности"

К примеру, если то левая сумма состоит из 41 члена, а правая состоит из 127 членов — тем не менее они оказываются равными при любом вещественном х.