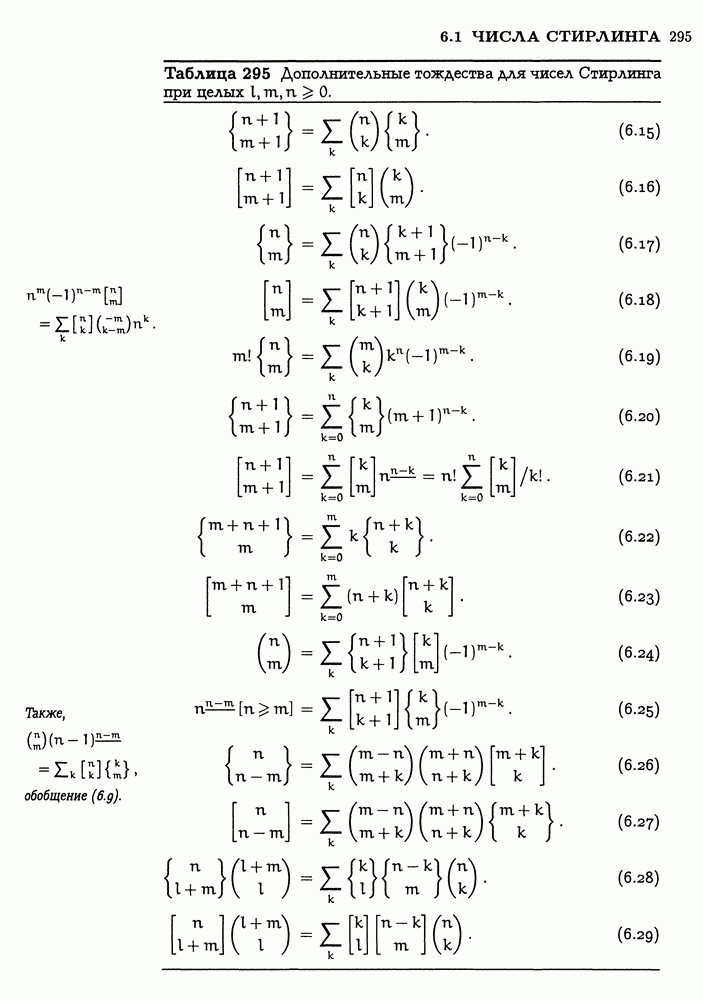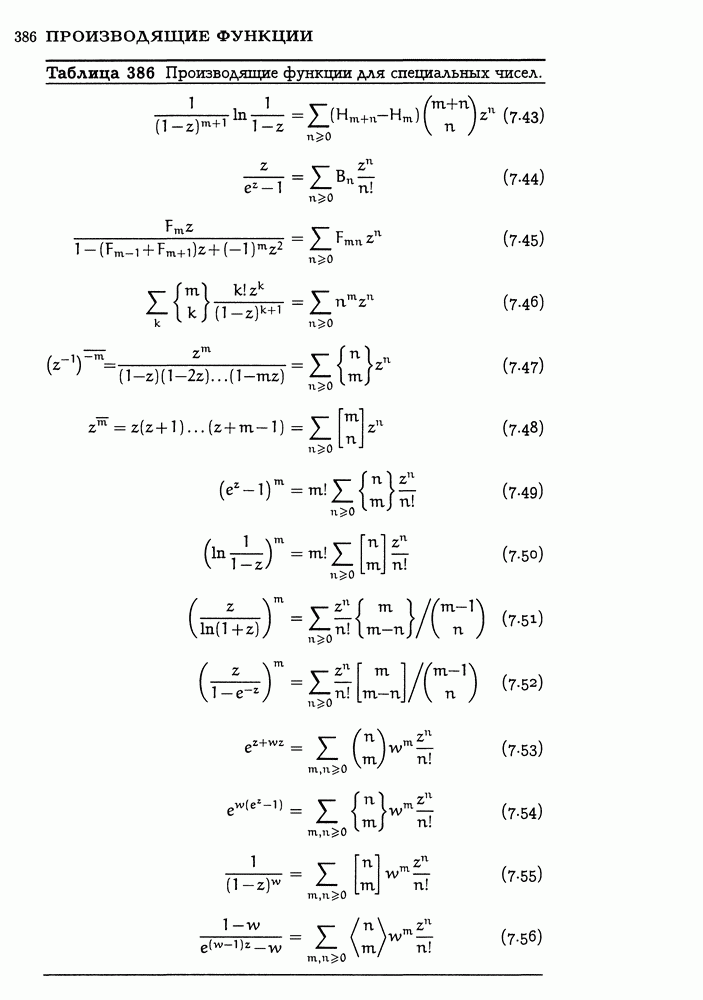5. Биномиальные коэффициенты

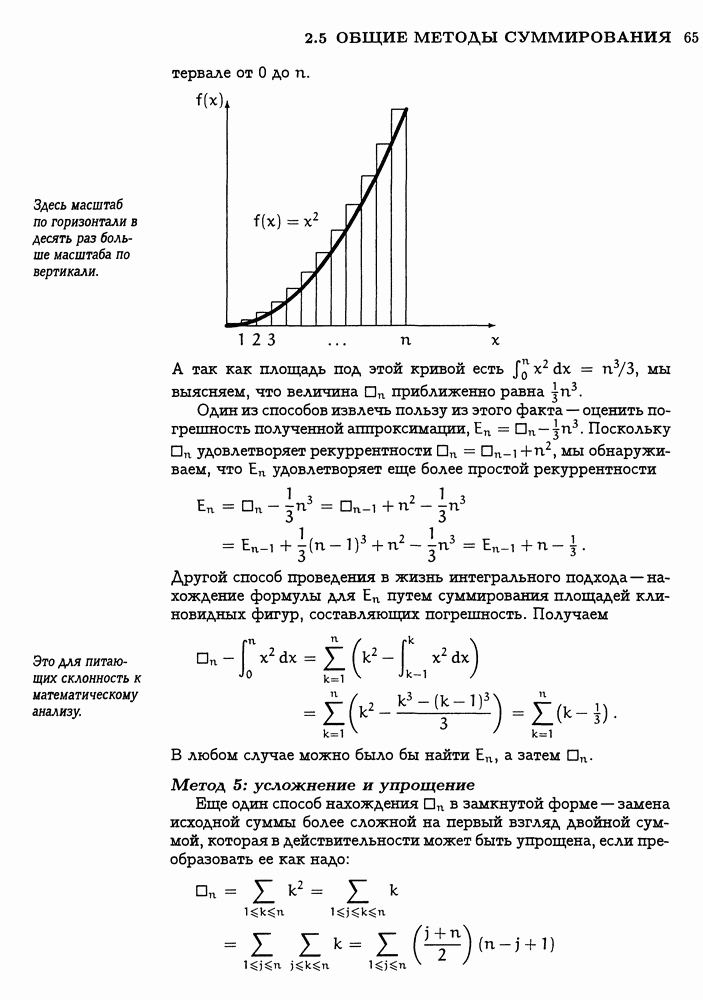
ПЕРЕВЕДЕМ ДУХ. В предыдущих главах нам порой приходилось нелегко с суммами, включавшими в себя пол-, потолок, mod-, фи- и мю-функции. А сейчас нам придется заняться биномиальными коэффициентами, которые оказываются (а) более важными в приложениях и более удобными в обращении, чем все отмеченные величины.

5.1 ОСНОВНЫЕ ТОЖДЕСТВА

Символ — это биномиальный коэффициент, своим названием обязанный биномиальной теореме — важному соотношению, которое мы рассмотрим позже в этом разделе. А читается этот символ как выбор из Подобное заклинание проистекает из его комбинаторной интерпретации — это число способов выбора -элементного подмножества из -элементного множества. Скажем, два элемента из множества можно выбрать шестью способами,

Для того чтобы выразить величину в более привычных терминах, удобнее всего вначале установить не число подмножеств, а число -элементных последовательностей, выбранных из -элементного множества; в последовательностях учитывается порядок элементов. Воспользуемся тем же соображением, которым мы пользовались в гл. 4, доказывая, что — это число перестановок из объектов. Существует вариантов выбора первого элемента последовательности, для каждого из них существует вариантов выбора второго элемента и т.д., вплоть до вариантов выбора элемента, что дает в итоге вариантов выбора. А поскольку каждое -элементное подмножество может быть упорядочено к! различными способами, это число последовательностей учитывает каждое подмножество ровно к! раз. Чтобы получить

требуемое, мы просто делим на

Так,

что согласуется с нашим предыдущим перечислением.

Назовем верхним индексом, а к — нижним индексом. В соответствии с их комбинаторной интерпретацией эти индексы ограничены неотрицательными целыми числами, так как множества не могут иметь отрицательное или дробное число элементов. Однако биномиальные коэффициенты полезны не только своей комбинаторной трактовкой, а посему от некоторых ограничений будем избавляться. Оказывается, что полезнее всего считать верхний индекс произвольным вещественным (или даже комплексным) числом, а нижний — произвольным целым числом. Соответственно, наше формальное определение принимает следующий вид:

Это определение обладает рядом заслуживающих внимания особенностей. Во-первых, верхний индекс обозначен через а не через — буква подчеркивает, что биномиальные коэффициенты сохраняют смысл и тогда, когда в этом месте оказывается любое вещественное число. Так, Несмотря на отсутствие комбинаторного смысла, случай оказывается одним из важнейших частных случаев. Некоторые нецелые индексы, типа также оказываются полезными.

Во-вторых, можно рассматривать как многочлен степени относительно Мы увидим, что такая точка зрения часто бывает плодотворной.

В-третьих, мы оставили неопределенными биномиальные коэффициенты при нецелых нижних индексах. Можно дать приемлемое определение и в этом случае, но на практике такие коэффициенты редко бывают нужны, поэтому мы отложим подобное обобщение и займемся им позднее в этой главе.

И последнее. В правой части нашего определения приведены ограничения . Подобные ограничения будут приводиться во всех рассматриваемых соотношениях с тем, чтобы была ясна область их применимости. Вообще-то, чем меньше ограничений, тем лучше: самое лучшее — соотношение без ограничений; но уж если они присутствуют, то составляют

важную часть соотношения. При манипуляциях с биномиальными коэффициентами проще на некоторое время забыть о трудных для запоминания ограничениях, а затем проверить, не были ли они нарушены. Но о проверке забывать нельзя.

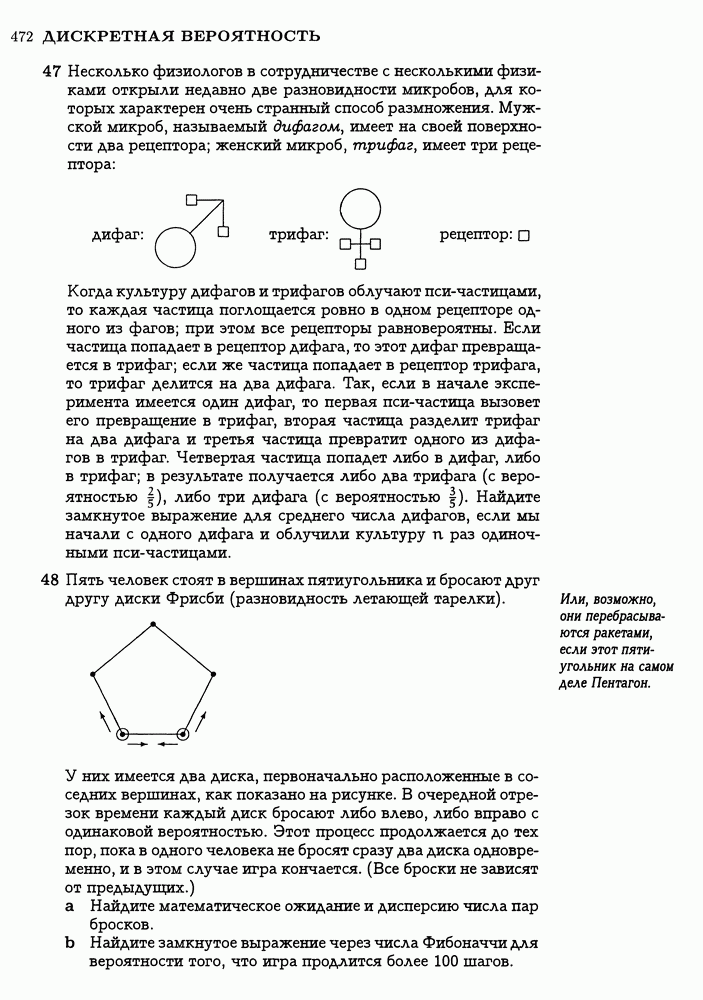
Так, практически всякий раз, когда мы сталкиваемся с коэффициентом (?), он оказывается равным 1, а потому можно впасть в заблуждение, что он всегда равен 1. Но внимательное рассмотрение определения (5.1) показывает, что равен 1 только при (при условии, что целое); если же то . И такие ловушки могут (и будут) подстерегать нас на каждом шагу.

Прежде чем приступить к тождествам, которыми мы будем пользоваться для укрощения строптивых биномиальных коэффициентов, бросим взгляд на несколько их начальных значений. Числа в табл. 180 образуют начало треугольника Паскаля, названного так по имени Блеза Паскаля (1623-1662), написавшего о них основополагающий трактат [233].

Таблица 180 Треугольник Паскаля

Пустые места в этой таблице на самом деле означают нуля в числителе (5.1); к примеру, Эти места оставлены пустыми просто для того, чтобы выделить остальную часть таблицы.

Не мешает запомнить формулы для первых трех колонок:

они справедливы при любом вещественном (Вспомните, что - это формула для треугольных чисел, которую мы вывели в гл. 1; эти числа сразу же бросаются в глаза в колонке (2) табл. 180.) Неплохо также запомнить около пяти первых рядов треугольника Паскаля: если в какой-нибудь задаче встретится набор чисел 1, 4, 6, 4, 1, то мы можем предположить, что где-то поблизости притаились биномиальные коэффициенты.

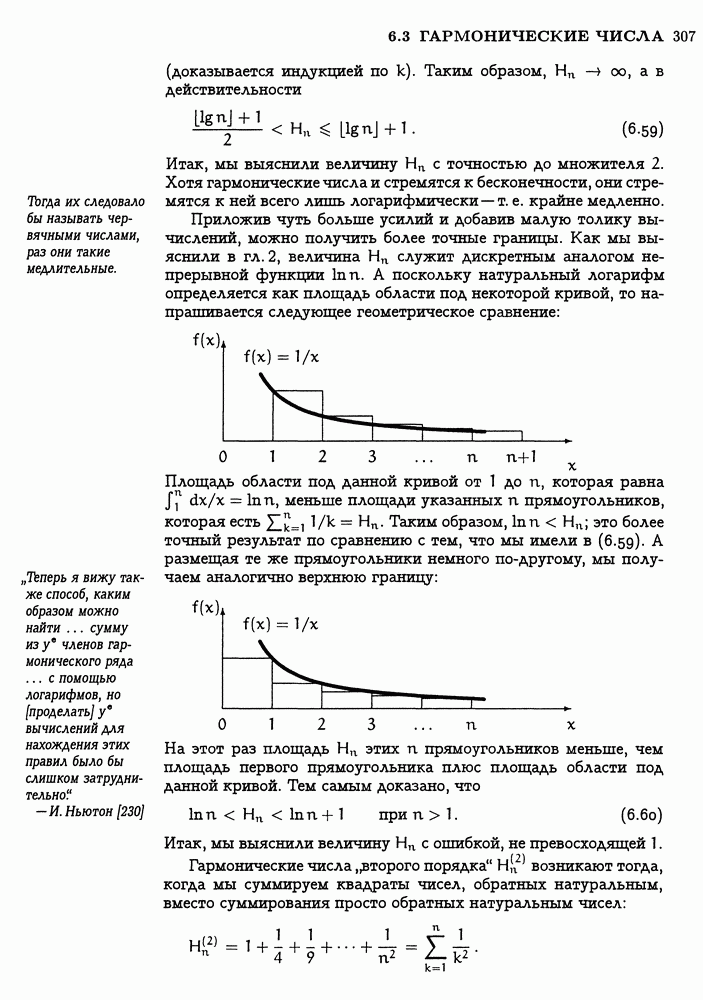
Числа в треугольнике Паскаля удовлетворяют практически бесконечному числу тождеств, так что неудивительно, если при его внимательном рассмотрении мы обнаружим ряд удивительных закономерностей. Вот, например, любопытное „свойство шестиугольника", которое иллюстрируется шестью числами 56, 28, 36, 120, 210, 126, окружающими число 84 в нижней правой части табл. 180. Два варианта перемножения чисел из этого шестиугольника через одно дают одинаковый результат: . То же самое справедливо, если выделить подобный шестиугольник из любой другой части треугольника Паскаля.

А теперь — собственно тождества. Наша цель в этом разделе — выучить сравнительно небольшое число простых правил, с помощью которых можно решать подавляющее большинство практически важных задач с биномиальными коэффициентами.

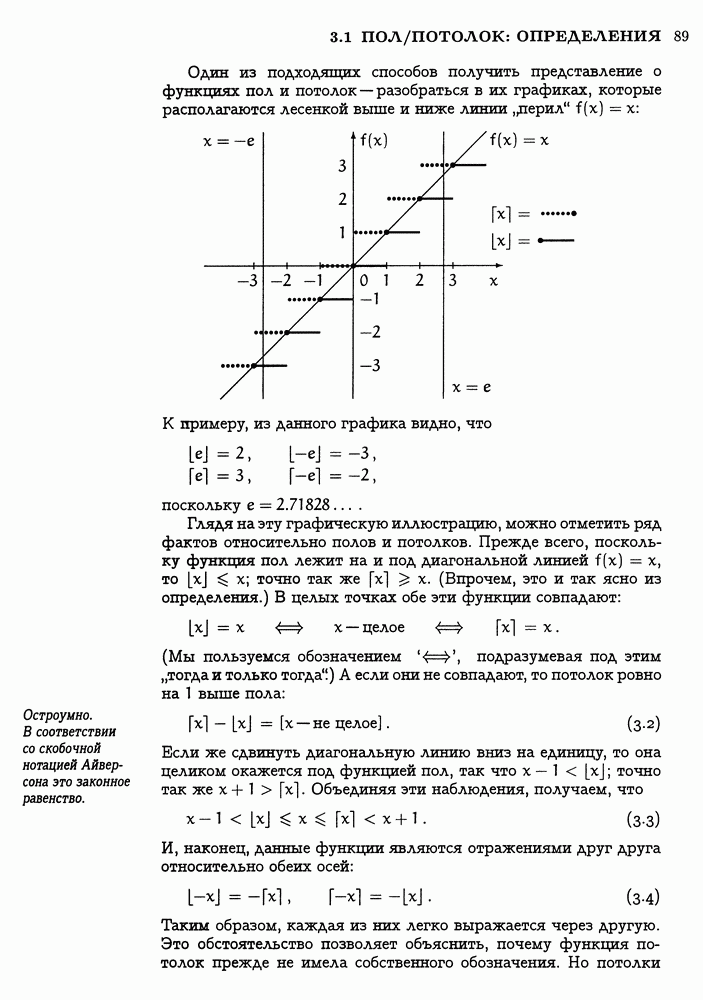
В обычном случае, когда верхним индексом является некоторое целое большее или равное нижнему индексу к, определению (5.1) может быть придана иная форма — в виде факториалов:

Для того чтобы получить эту формулу, просто умножаем числитель и знаменатель (5.1) на . Порой бывает полезно выразить биномиальный коэффициент в подобной факториальной форме (скажем, при доказательстве „свойства шестиугольника"). Но зачастую приходится действовать в обратном направлении, заменяя факториалы биномиальными коэффициентами.

Факториальное представление указывает на симметричность треугольника Паскаля: каждый ряд читается одинаково — как слева направо, так и справа налево. Тождество, отражающее это свойство, — соотношение симметрии — получается заменой к на :

Эта формула имеет комбинаторный смысл, ибо определяя к предметов, выбранных из мы тем самым определяем — к невыбранных предметов.

Ясно, почему и к в тождестве (5.4) ограничены целыми числами — потому что всякий нижний индекс должен быть целым числом. Но почему не может быть отрицательным? К примеру, предположим, что Верно ли равенство

Увы. В частности, при в левой части получается 1, а в правой — 0. На самом деле при всяком целом к 0 левая часть

равна

т. е. либо 1, либо —1, но правая часть равна 0, так как нижний индекс отрицателен. А при отрицательном к левая часть равна О, но правая часть равна

т. е. либо 1, либо —1. Так что равенство всегда неверно!

Соотношение симметрии не выполняется и при прочих отрицательных целых . Но, к сожалению, это ограничение легко забывается, поскольку выражение в верхнем индексе порой бывает отрицательным лишь при некоторых малозаметных (но существующих) значениях его переменных. Всякий, кто много раз имел дело с биномиальными коэффициентами, попадался в эту ловушку не менее трех раз.

Однако этот недостаток соотношения симметрии компенсируется существенным его достоинством: оно выполняется при всех значениях к, даже когда или (ибо в таких случаях обе части равны нулю). В случае же, когда 0 к , симметрия немедленно следует из (5.3):

Следующее важное тождество допускает вынесение и внесение из/под знака биномиального коэффициента:

Данное ограничение на к предохраняет нас от деления на нуль. Назовем тождество (5.5) правилом внесения, поскольку, как правило, мы пользуемся им для внесения под знак биномиального коэффициента некоторой мешающей переменной. Это равенство вытекает из определения (5.1), так как при , а при обе части равны нулю.

Если умножить обе части (5.5) на к, то получим правило внесения, которое выполняется даже при

У этого соотношения есть компаньон, который сохраняет нижний индекс в неприкосновенности:

Тождество (5.7) можно вывести, приготовив сэндвич из двух соотношений симметрии и одного правила внесения между ними:

Но постойте-ка! Мы уже объявили, что данное тождество справедливо при любом вещественном а ведь проведенный вывод справедлив, только когда — целое положительное число. (Если мы не собираемся использовать условие симметрии (5.4) себе во вред, то верхний индекс должен быть целым неотрицательным числом.) Может, мы смошенничали? Вовсе нет. Да, это верно, что данный вывод справедлив при целом положительном и, тем не менее, можно утверждать, что данное тождество выполняется при всех значениях в силу того, что обе части (5.7) являются многочленами степени относительно Ненулевой многочлен степени или меньшей может иметь самое большее различных нулей — следовательно, разность двух таких многочленов, которая также является многочленом степени или меньшей, не может обращаться в нуль более чем в точках, если только она не равна тождественно нулю. Иначе говоря, если два многочлена степени совпадают более чем в точках, то они совпадают во всех точках. Нами показано, что является тождеством всякий раз, когда — целое положительное число, так что эти два многочлена совпадают в бесконечном числе точек, а значит, тождественно равны.

Способ доказательства из предыдущего абзаца, который мы будем называть полиномиальной аргументацией, полезен при перенесении многих соотношений, справедливых для целых чисел, на вещественные числа — мы неоднократно это увидим. Некоторые равенства, типа соотношения симметрии (5.4), не являются тождествами для многочленов, так что мы не всегда сможем применять этот способ. Тем не менее, многие соотношения имеют нужный вид.

Вот, к примеру, еще одно полиномиальное тождество — возможно, самое важное из всех биномиальных тождеств — известное как формула сложения:

Если — целое положительное число, то формула сложения показывает, что каждое число в треугольнике Паскаля есть сумма двух чисел предыдущего ряда — того, что непосредственно над

ним, и того, что рядом слева от него. Эта формула применима также при отрицательном, вещественном или комплексном с единственным ограничением, чтобы к было целым (с тем, чтобы биномиальные коэффициенты были определены).

Один из способов доказать формулу сложения — предположить, что — целое положительное число, и воспользоваться комбинаторными соображениями. Вспомним, что — это число всевозможных -элементных подмножеств, выбранных из -элементного множества. Если у нас яиц, среди которых одно тухлое, то имеется способов выбора к яиц. Ровно в случаях результатом этих выборов будут только свежие яйца, а в случаях среди них окажется тухлое яйцо, ибо результатом таких выборов будет из свежих яиц. Складывая два этих числа, получаем (5.8). В этом выводе предполагается, что — целое положительное число и что к 0. При обе части данного тождества равны нулю, а во всех остальных случаях справедливость тождества (5.8) устанавливается путем полиномиальной аргументации.

Тождество (5.8) можно также вывести, складывая два правила внесения-вынесения (5.7) и (5.6):

левая часть это следовательно, можно разделить обе части на Этот вывод справедлив при всех за исключением случая который легко проверить отдельно.

Те из нас, кто не склонен отыскивать столь тонкие доказательства, или те, кому это, напротив, надоело, могли бы предпочесть вывести (5.8) путем непосредственного манипулирования с исходным определением. Если то

И опять случаи при к 0 легко проверить отдельно.

Мы только что познакомились с тремя весьма различными доказательствами формулы сложения. И это не удивительно: биномиальные коэффициенты обладают большим разнообразием свойств, различие которых обязано приводить к различным доказательствам интересующего нас соотношения.

В сущности, формула сложения — это рекуррентность для чисел из треугольника Паскаля, и мы еще увидим, что она особенно полезна при доказательстве других тождеств по индукции.

А можно и немедленно получить новое тождество, развертывая данную рекуррентность. Так,

Поскольку последний член пропадает и можно остановиться. Этот метод дает общую формулу:

Обратите внимание, что нет необходимости ограничивать индекс суммирования снизу, поскольку все члены суммы при равны нулю.

Эта формула выражает один биномиальный коэффициент в виде суммы других, верхний и нижний индексы которых остаются „равноудаленными". Мы нашли ее путем последовательного разложения биномиальных коэффициентов с наименьшим нижним индексом: вначале коэффициента , затем коэффициента , потом коэффициента и, наконец, коэффициента . А что случится, если развернуть другим способом — последовательно разлагая коэффициенты с наибольшим нижним индексом? Посмотрим:

Теперь коэффициент (3) равен нулю (так же, как хотя они и придают данному соотношению некоторую привлекательность), и можно уловить общую закономерность:

Это тождество, которое мы назовем формулой суммирования по верхнему индексу, выражает один биномиальный коэффициент в виде суммы других, нижние индексы которых не изменяются. В данном случае сумма нуждается в нижней границе к 0, так как члены суммы с не нули. К тому же вообще не могут быть отрицательными.

Тождество (5.10) допускает интересную комбинаторную трактовку. Если нужно выбрать из билетов, пронумерованных числами от 0 до то это можно сделать способами, если наибольший номер выбранного билета равен к.

Как соотношение (5.9), так и соотношение (5.10) можно доказать по индукции, используя формулу сложения, но можно также получить одно соотношение из другого. Давайте, например, получим (5.9) из (5.10): доказательство послужит иллюстрацией некоторых стандартных операций с биномиальными коэффициентами. В общих чертах план действия таков: сначала преобразовать левую часть соотношения (5.9) таким образом, чтобы она выглядела как левая часть соотношения (5.10); затем прибегнуть к помощи последнего соотношения, заменив всю сумму одним-единственным биномиальным коэффициентом; наконец, привести этот коэффициент к виду правой части (5.9).

Для удобства предположим, что — целые неотрицательные числа; в общем случае соотношение (5.9) будет получаться из этого частного случая в соответствии с полиномиальной аргументацией. Условимся писать вместо потому, что эта переменная больше напоминает целое неотрицательно число. Теперь можно приступить к систематическому воплощению нашего плана:

Шаг за шагом проследим за этим выводом. Решающий шаг сделан во второй строке, где мы применяем правило симметрии (5.4),

чтобы заменить на . А это можно сделать только при , так что первый шаг ограничивает область изменения к, отбрасывая члены суммы с (что законно, поскольку отброшенные члены равны нулю). Теперь мы почти готовы применить (5.10): третья строчка готовит почву для этого, заменяя к на m и приводя в порядок диапазон суммирования. Этот шаг, подобно первому, — просто заигрывание с -обозначением. Но теперь к собственной персоной появляется в верхнем индексе, да и пределы суммирования приведены в надлежащий вид, так что в четвертой строчке применяется (5.10). В завершение всего еще раз используется правило симметрии.

Некоторые суммы, с которыми мы имели дело в гл. 1 и 2, на самом деле являются либо частными случаями соотношения (5.10), либо скрытыми вариантами этого соотношения. К примеру, случай доставляет сумму неотрицательных целых чисел до включительно:

А общий случай эквивалентен правилу

из гл. 2, если разделить обе части этой формулы на . И в самом деле, формула сложения (5.8) указывает, что

если заменить соответственно на . Следовательно, методы из гл. 2 обеспечивают нас удобной формулой неопределенного суммирования:

Своим названием биномиальные коэффициенты обязаны биномиальной теореме, которая имеет дело со степенями бинома . Вот простейшие случаи этой теоремы:

Нетрудно понять, почему эти коэффициенты совпадают с числами треугольника Паскаля. Когда мы расписываем произведение

каждый его член сам является произведением сомножителей х и у. Число таких членов с к сомножителями сомножителями у после приведения подобных членов становится коэффициентом при . А это в точности равно числу способов выбора к из двучленов, из которых в произведение войдет х, т. е. это

В некоторых учебниках величину 0° оставляют неопределенной, объясняя это тем, что функции имеют различные пределы, когда х стремится к 0. Но это заблуждение. Необходимо определить

с тем чтобы биномиальная теорема была верна при и/или . Эта теорема слишком важна, чтобы ее произвольно ограничивать! И, напротив, функция совсем не важна. (См. дальнейшие обсуждения в

А что именно представляет собой биномиальная теорема? Во всем своем великолепии она выступает в обличии следующего тождества:

Это сумма по всем целым к, но в действительности при целом неотрицательном это конечная сумма, поскольку все ее члены равны нулю, за исключением членов с 0 к . С другой стороны, биномиальная теорема верна и при отрицательном и даже при произвольном вещественном или комплексном . В таких случаях данная сумма действительно бесконечна и требуется, чтобы для гарантии абсолютной сходимости суммы.

Два частных случая биномиальной теоремы заслуживают особого внимания, несмотря на то, что они исключительно просты. Если неотрицательно, то

Это равенство показывает, что сумма чисел ряда треугольника Паскаля равна . А если х вместо равен —1, то

К примеру, если снабдить элементы ряда чередующимися знаками, то их сумма равна нулю, за исключением верхнего ряда (когда

Таблица 189 Продолженный вверх треугольник Паскаля.

Если не является неотрицательным целым, то биномиальная теорема чаще всего используется в частном случае Сформулируем этот частный случай явно, заменив х на чтобы подчеркнуть тот факт, что здесь может присутствовать произвольное комплексное число:

Если подставить сюда и умножить обе части на то из этой формулы вытекает общая формула (5.12).

Мы доказали, исходя из комбинаторной интерпретации, биномиальную теорему только для целого неотрицательного Мы лишены возможности вывести формулу для общего случая из случая целого неотрицательного используя полиномиальную аргументацию, ибо в общем случае сумма бесконечна. Однако в случае произвольного можно воспользоваться теоремой Тейлора из анализа:

Производные функции легко вычисляются: в самом деле, . А подстановка дает (5.13).

Кроме того, нужно доказать, что бесконечная сумма сходится при . И это действительно так, поскольку согласно равенству (5.83), которое приводится ниже.

А теперь займемся вплотную величинами при целом отрицательном Один из способов подступиться к этим величинам состоит в том, чтобы использовать правило сложения (5.8) для заполнения табл. 180 элементами, которые лежат выше имеющихся чисел, получая тем самым табл. 189. К примеру, так как затем так как

Все эти числа нам уже знакомы. Действительно, ряды и колонки из табл. 189 оказываются колонками из табл. 180 (за вычетом

знака „минус"). Так что между величинами при отрицательных и положительных должна существовать некая связь. Общее правило таково:

что легко доказать, поскольку

при к 0, а при обе части равны нулю.

Особенно ценно то, что соотношение (5.14) выполняется без всяких ограничений. (Разумеется, нижний индекс должен быть целым с тем, чтобы были определены биномиальные коэффициенты.) Преобразование (5.14) называется обращением верхнего индекса, или просто „верхним обращением"

Но как запомнить эту важную формулу? Если все соотношения, с которыми мы уже имели дело, — соотношения симметрии, внесения, сложения и т. п. - были довольно бесхитростны, то это соотношение выглядит весьма замысловато. Тем не менее, существует мнемоническое правило, что само по себе не так уж и плохо. Обращение верхнего индекса начинается с записи , где к — нижний индекс. (Нижний индекс не должен изменяться.) Затем мы сразу же снова записываем к дважды: на места верхнего и нижнего индексов. Потом обращается исходный верхний индекс путем его вычитания из нового верхнего индекса. И в завершение вычитается еще 1 (всегда вычитая, а не прибавляя, ибо это процесс обращения).

Для закрепления материала два раза подряд обратим верхний индекс. Имеем

и мы вернулись к тому, с чего начали. Вряд ли это то, к чему мы стремились, воссоздав данное соотношение, — но приятно сознавать, что мы не сбились с пути.

Разумеется, имеются более полезные применения соотношения (5.14), чем это. Так, верхнее обращение можно использовать для перемещения величин из верхнего на место нижнего индекса и наоборот. Соответствующее соотношение имеет симметричную форму:

ибо обе части равны

Кроме того, верхнее обращение может быть использовано для вывода следующей интересной формулы суммирования:

Идея вывода этой формулы состоит в том, чтобы сперва обратить верхний индекс, затем применить формулу (5.9), а потом снова обратить индекс:

Эта формула дает частичную сумму ряда треугольника Паскаля, при условии что элементам данного ряда приписаны чередующиеся знаки. Так, при эта формула дает

Обратите внимание, что при формула (5.16) дает знакочередующуюся сумму элементов всего ряда, а такая сумма равна нулю при целом положительном Это уже было доказано при разложении в соответствии с биномиальной теоремой — интересно то, что частичные суммы такого разложения могут быть вычислены в замкнутой форме.

А как насчет более простой частичной суммы

Если мы умеем вычислять соответствующую знакочередующуюся сумму, то наверняка должны суметь вычислить и эту. А вот и нет: для частичной суммы элементов ряда треугольника Паскаля не существует замкнутого выражения. Мы умеем вычислять суммы элементов в колонках — это формула (5.10), - но не в рядах. Любопытно, однако, что можно вычислить частичные суммы элементов ряда, если умножить их на расстояние от центра:

(Эта формула легко проверяется индукцией по ) Взаимосвязь между этими частичными суммами — имеющими и не имеющими

множитель в общем члене — аналогична взаимосвязи между интегралами

Явно более сложный интеграл слева с множителем х выражается в замкнутой форме, в то время как более простой на вид интеграл справа без такого множителя — не выражается. Внешность бывает обманчивой.

В конце этой главы мы разберем метод, с помощью которого можно определить, выражаются или нет в замкнутой форме частичные суммы некоторого заданного ряда с биномиальными коэффициентами — в достаточно общей постановке. Данный метод в состоянии обнаружить формулы (5.16) и (5.18), а также позволяет выяснить, что нахождение формулы для (5.17) - гиблое дело.

Частичные суммы биномиального ряда приводят к другого рода любопытному соотношению:

Не составляет труда доказать это соотношение по индукции: при обе части равны нулю, а при равны 1. Если обозначить сумму в левой части через то, воспользовавшись формулой сложения (5.8), легко показать, что

и

при m > 0. Следовательно,

а правая часть (5.19) также удовлетворяет этому рекуррентному соотношению. По индукции, обе части должны быть равны —

Но есть более тонкое доказательство. Если — целое число из промежутка то биномиальная теорема показывает, что обе части (5.19) равны . А поскольку обе части

представляют собой многочлены относительно степени или меньшей, то совпадения их только в различных точках достаточно (но только-только!) для установления равенства в общем случае.

Вроде бы глупо обзаводиться соотношением, где одна сумма равна другой. Тем более, что ни одна из них не выражается в замкнутой форме. Но иногда вычислить одну сумму оказывается проще, чем другую. К примеру, если положить то получим альтернативную форму соотношения (5.16):

А если положить то получим

В левой части просуммирована только половина биномиальных коэффициентов с верхним индексом а эти коэффициенты равны своим двойникам в правой половине, поскольку треугольник Паскаля обладает лево-правосторонней симметрией. Следовательно, левая часть — это просто и мы получаем формулу, которую никак не ожидали получить:

Проверим ее при Поразительно, но факт.

До сих пор мы рассматривали либо отдельные биномиальные коэффициенты, либо суммы, в члены которых входило только по одному биномиальному коэффициенту. Но многие из бросающих нам вызов задач включают в себя произведения двух и более биномиальных коэффициентов, поэтому оставшуюся часть этого раздела мы посвятим рассмотрению именно таких случаев.

Вот удобное правило, которое зачастую помогает упростить произведение двух биномиальных коэффициентов:

Мы уже встречались с частным случаем — правилом внесения Хотя как одна, так и другая части (5.21) суть произведения биномиальных коэффициентов, зачастую одну из них просуммировать проще, чем другую, благодаря взаимодействию с другими частями формулы. Так, встречается в левой части дважды, а в правой — лишь однажды. Поэтому при суммировании по мы, естественно, предпочитаем заменить на

Равенство (5.21) справедливо исключительно по причине взаимного сокращения в факториальных представлениях Если все переменные — целые числа , то

Здесь не было ничего сложного. К тому же, если или то обе части (5.21) равны нулю, так что данное соотношение выполняется при любых целых . Наконец, посредством полиномиальной аргументации его можно распространить на все вещественные

Биномиальный коэффициент вида можно переписать в виде после соответствующего переобозначения переменных. Аналогично, величину в середине предыдущей выкладки можно переписать в виде . Это „триномиальный коэффициент" который возникает в „триномиальной теореме":

Таким образом, - это на самом деле триномиальный коэффициент в другом обличии. Время от времени триномиальные коэффициенты возникают в приложениях, и их обычно записывают как

чтобы подчеркнуть наличие симметрии.

Обобщением биномиальных и триномиальных коэффициентов служат мультиномиальные коэффициенты, которые всегда выражаются в виде произведения биномиальных коэффициентов:

Таблица 195 Суммы произведений биномиальных коэффициентов.

А потому, при встрече с подобным страшилищем, нам поможет наше испытанное оружие.

Вот мы и добрались до табл. 195, в которой перечислены наиболее важные из числа испытанных нами тождеств. Это те тождества, на которые мы опираемся в противоборстве с суммой, включающей в себя произведение двух биномиальных коэффициентов. Каждое из этих тождеств представляет собой сумму по к с одним к в каждом биномиальном коэффициенте; помимо этого, в нее входит по четыре почти не зависящих друг от друга параметра, обозначаемых через и т.д., — по одному на месте каждого индекса. В зависимости от того, входит или нет к в верхний или нижний индекс, а также от того, с каким знаком он входит, мы имеем дело с разными случаями. А в некоторых случаях имеется и дополнительный множитель необходимый для того, чтобы сумма вычислялась в замкнутой форме.

Таблица 195 слишком уж сложна для запоминания; она предназначена только для справок. Однако первое тождество из этой таблицы запоминается гораздо легче остальных и его не следует забывать. Оно устанавливает, что сумма (по всем целым к) произведения двух биномиальных коэффициентов, в которых верхние индексы постоянны порознь, а нижние индексы постоянны в сумме при любом к, равна биномиальному коэффициенту, полученному путем сложения как верхних, так и нижних индексов. Данное тождество известно как свертка Вандермонда, поскольку Александр Вандермонд написал по этому поводу в конце 18-го века важную статью [45]; однако еще в 1303 г. оно было известно Чжу Ши-цзе из Китая. Все остальные тождества в табл. 195 можно получить из свертки Вандермонда, аккуратно выполняя преобразования обращения верхнего индекса, применяя правило

симметрии и т. п., - следовательно, свертка Вандермонда является „самым основным" из всех основных тождеств.

Правило свертки Вандермонда можно доказать, исходя из замечательной комбинаторной интерпретации. Если заменить к на , а на то можно считать, что следовательно, требуется доказать тождество

Пусть — целые неотрицательные числа (общий случай получается посредством полиномиальной аргументации). В правой части — это число способов выбрать человек из мужчин и женщин. В левой части каждый член суммы — это число способов выбрать к человек из мужчин и человек из женщин. А суммирование по всем к учитывает каждую возможность ровно по одному разу.

Как правило, эти тождества применяются слева направо, так как упрощение идет именно в этом направлении. Но иногда оправданно движение в обратном направлении, даже если приходится временно идти на усложнение. При этом обычно образуется двойная сумма, в которой можно изменить порядок суммирования и потом упростить.

Перед тем как двинуться дальше, посмотрим, как доказываются еще два тождества из табл. 195. Тождество (5.23) доказать легко: нужно всего лишь заменить первый биномиальный коэффициент на а потом применить свертку Вандермонда (5-22).

Следующее тождество, (5.24), несколько сложнее. Путем последовательных преобразований его можно свести к свертке Вандермонда, но можно доказать его столь же просто, если прибегнуть к старому испытанному методу математической индукции. Зачастую индукция — это первое, к чему мы прибегаем, если в голову не приходит ничего другого, но здесь индукция по I подходит как нельзя лучше.

Действительно, при все члены суммы равны нулю, за исключением члена с так что обе части данного равенства равны . А теперь предположим, что данное тождество справедливо при всех значениях, меньших некоторого фиксированного I, где Можно воспользоваться формулой сложения для замены на тогда первоначальная сумма распадается на две суммы, каждую из которых можно вычислить, исходя из предположения

А если еще раз применить формулу сложения, то это упрощается и получается правая часть (5.24).

В этом выводе заслуживают внимания две вещи. Во-первых, мы вновь убеждаемся в огромном преимуществе суммирования по всем целым к, а не по к в определенных пределах, поскольку не нужно беспокоиться по поводу граничных условий. Во-вторых, формула сложения чудесно стыкуется с математической индукцией, поскольку она представляет рекуррентную зависимость для биномиальных коэффициентов. Биномиальный коэффициент, верхний индекс которого есть I, выражается в виде суммы двух коэффициентов, верхние индексы которых суть это именно то, что требуется для предположения индукции.

Пожалуй, хватит о табл. 195. А что можно сказать о суммах с тремя и более биномиальными коэффициентами? Если индекс суммирования разбросан по всем коэффициентам, то шансы отыскать сумму в замкнутой форме невелики: известно лишь несколько сумм такого рода, которые выражаются в замкнутой форме, и нужная нам сумма вполне могла не соответствовать предъявленным требованиям. Одна из таких редкостей, доказанная в упр. 43, это сумма

А вот другой, более симметричный экземпляр:

У него есть двойник с двумя коэффициентами:

который, между прочим, не фигурирует в табл. 195. Аналогичная сумма с четырьмя коэффициентами не выражается в замкнутой форме, зато выражается другая подобная ей сумма:

Это было обнаружено Джоном Дуголом [111] в начале двадцатого столетия.

Является ли тождество Дугола самой лохматой из известных сумм биномиальных коэффициентов? Вовсе нет! Чемпионом такого рода до сих пор остается сумма

Это сумма по переменным индексам при Равенство всего лишь ее частный случай при в случае ее можно переписать следующим образом, если воспользоваться обозначениями вместо (си, вместо

Левая часть (5.31) — это коэффициент при получающийся после полного разложения произведения дробей

по положительным и отрицательным степеням z. Предположение о виде правой части (5.31) было высказано Фримэном Дайсоном в 1962 г. и вскоре после этого было доказано сразу несколькими людьми. В упр. 95 приводится „простое" доказательство (5.31).

Заслуживает внимания еще одно тождество, включающее в себя массу биномиальных коэффициентов:

У данного тождества, доказанного в упр. 83, даже есть шансы встретиться в практических приложениях. Впрочем, мы уже отклоняемся от нашей темы „основные тождества" так что лучше остановиться и подвести итог пройденному материалу.

Мы убедились, что биномиальные коэффициенты удовлетворяют такому разнообразию тождеств, которое способно сбить

Таблица 199 Десять самых главных тождеств с биномиальными коэффициентами. (см. скан)

с толку. К счастью, некоторые из них легко запоминаются, и мы можем воспользоваться этим обстоятельством для выведения большинства других всего за несколько шагов. В табл. 199 сведены десять наиболее полезных формул. Это именно те тождества, которые следует хорошенько запомнить.