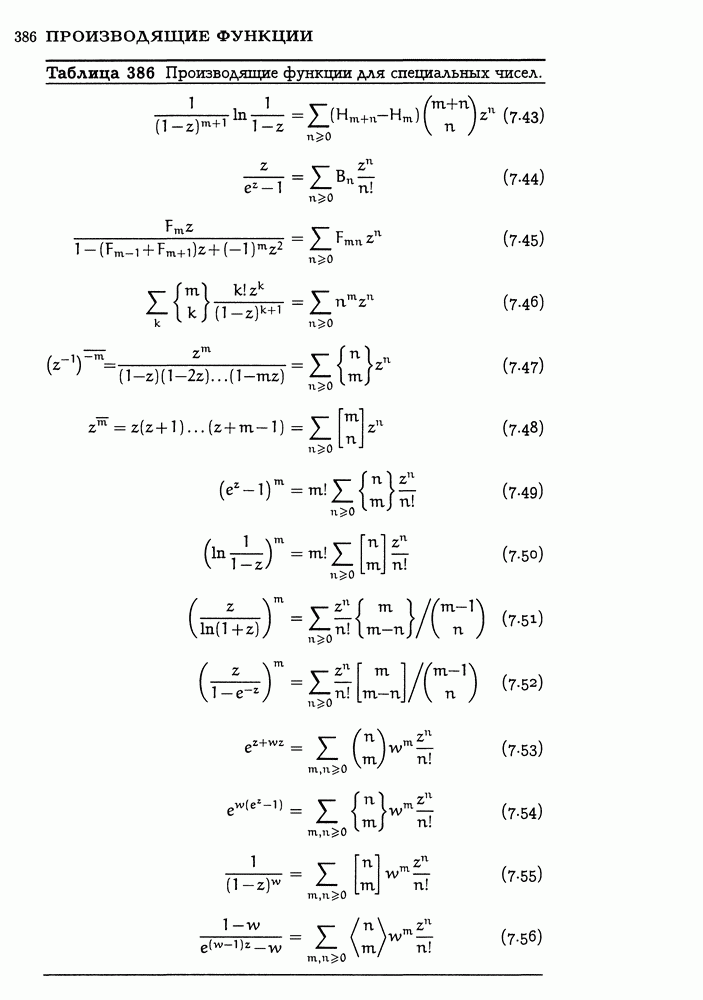6.7 КОНТИНУАНТЫ

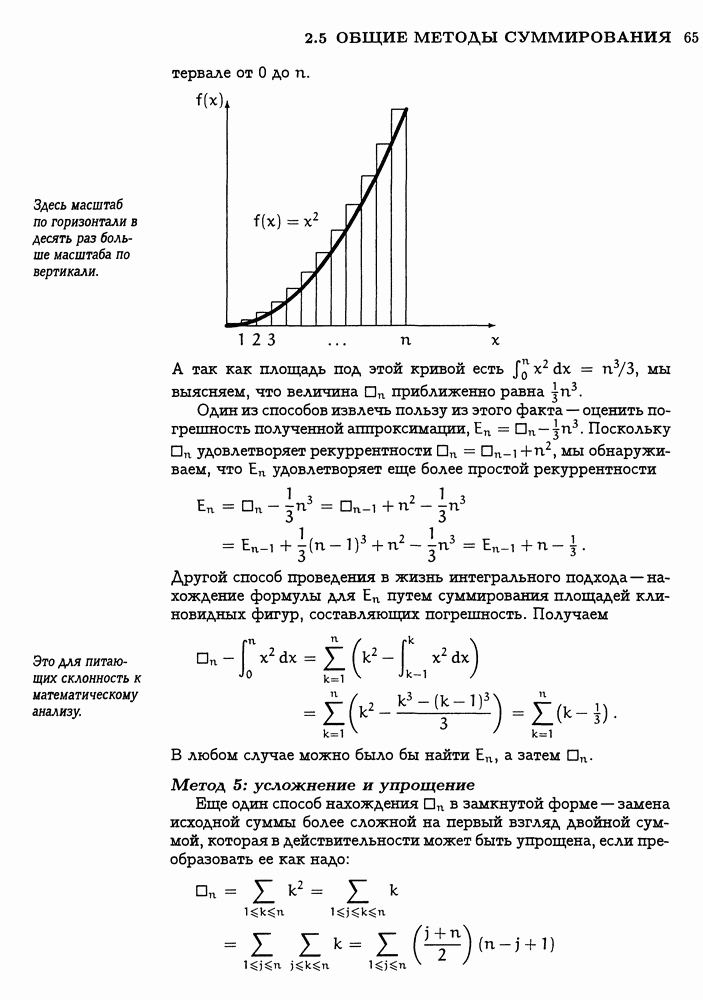
Числа Фибоначчи обнаруживают важные связи с деревом Штерна—Броко, которое мы изучали в гл. 4, и допускают важные обобщения на последовательность многочленов, которую обстоятельно изучал Эйлер. Эти многочлены называются континуантами

или К-многочленами, поскольку служат основой изучения континуальных (непрерывных) дробей — выражений вида

К-многочлен содержит переменных и определяется рекуррентно следующим образом:

Например, три следующих за случая таковы:

Отсюда индуктивно легко убедиться, что число членов в равно числу Фибоначчи:

Если число переменных ясно по смыслу, то вместо можно писать просто — точно так же, как можно было опускать число параметров, имея дело с гипергеометрическими функциями из гл. 5. Например, . Конечно же, в формулах типа (6.128) нижний индекс необходим.

Эйлер подметил, что многочлен может быть получен, если начать с произведения и затем вычеркивать соседние пары всеми возможными способами. Правило Эйлера можно представить графически, образуя всевозможные слова длины из точек и тире в «азбуке Морзе» где каждая точка дает длину 1, а каждое тире дает длину 2; вот слова длины 4 в азбуке Морзе:

Эти слова из точек и тире соответствуют членам точка означает переменную, которая включена, а тире означает пару переменных, которая исключена. Например, соответствует

Слово длины в азбуке Морзе, которое содержит к тире, содержит точек, а всего к знаков. Эти точки и тире могут быть расставлены способами; поэтому, если заменить каждую точку на а каждое тире — на 1, то получим

Кроме того, известно, что общее число членов в континуанте равно некоторому числу Фибоначчи. Следовательно, установлено тождество

(Выражение в замкнутой форме для (6.129), обобщающее формулу Эйлера—Вине (6.123) для чисел Фибоначчи, приведено в

Связь между К-многочленами и словами в азбуке Морзе показывает, что континуанты обладают зеркальной симметрией:

Поэтому, в дополнение к правосторонней рекуррентности из определения (6.127), они подчиняются рекуррентности, которая пристраивает переменные слева:

А обе эти рекуррентности являются частными случаями более общего правила:

Это правило легко истолковать, исходя из аналогии с азбукой Морзе: первое произведение дает те члены в которых нет тире в позиции в то время как второе произведение дает те члены, в которых в этой позиции тире присутствует. Если же положить все х равными 1, то данное тождество показывает, что таким образом, (6.108) — это частный случай (6.133).

Эйлер [376] обнаружил, что континуанты подчиняются еще более замечательному правилу, которое является обобщением соотношения Кассини:

Это правило (доказанное в упр. 29) справедливо тогда, когда индексы при всех К неотрицательны. Так, при имеем

К-многочлены тесно связаны с алгоритмом Евклида. Предположим, например, что вычисление оканчивается через четыре шага:

Тогда

И вообще, если алгоритм Евклида находит наибольший общий делитель через к шагов после вычисления последовательности частных это означает, что начальными числами были (Это обстоятельство было замечено еще в начале восемнадцатого века Тома Фанте де Ланьи [183], который, по-видимому, был первым, кто непосредственно рассматривал континуанты. При этом Ланьи отмечал, что последовательные числа Фибоначчи, которые фигурируют в качестве континуантов, когда принимают свои минимальные значения, являются теми наименьшими числами на входе, при которых алгоритму Евклида требуется некоторое заданное число шагов.)

Кроме того, континуанты тесно связаны с непрерывными дробями, от которых они получили свое название. К примеру,

Такая же картина наблюдается для непрерывных дробей любой „глубины" Это легко доказать по индукции; так

в силу соотношения

(Это соотношение доказано и обобщено в упр. 30.)

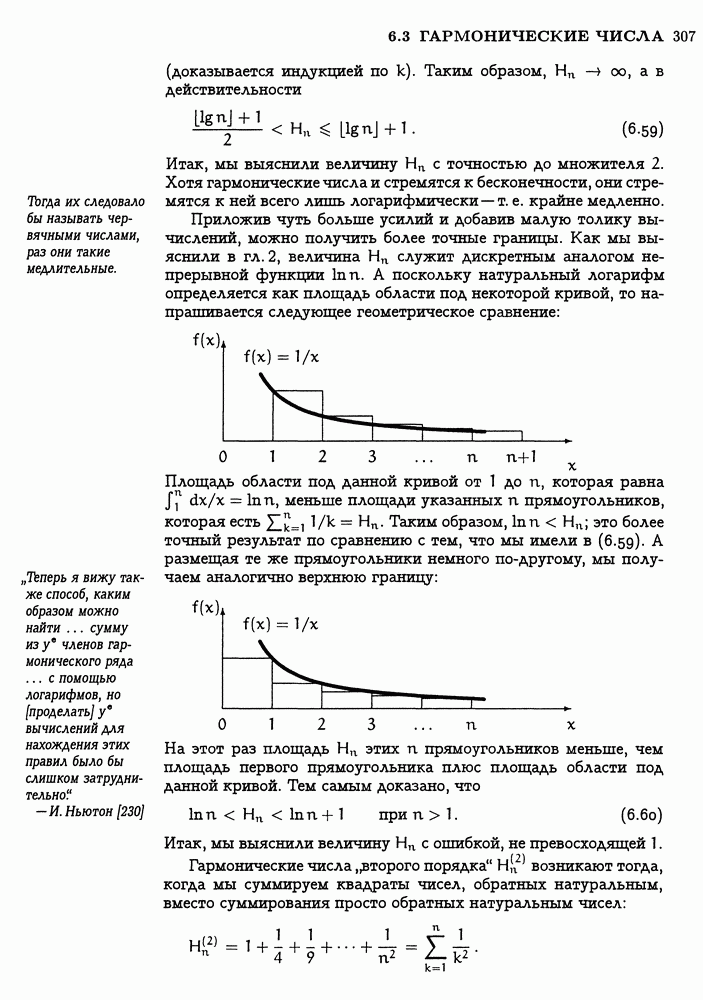
Сверх того, континуанты тесно связаны и с деревом Штерна—Броко, которое обсуждалось в гл. 4. Каждый узел этого дерева может быть представлен в виде последовательности скажем, в виде

где — четное. Используя -матрицы L и R из (4.33), нетрудно доказать по индукции, что матричным эквивалентом (6.137) является

(Доказательство этого составляет часть упр. 87.) Например,

В силу этого можно воспользоваться (4.34), чтобы записать, наконец, выражение в замкнутой форме для дроби из дерева Штерна—Броко, - представлением которой является (6.137):

(Это „теорема Халфена“ [329].) К примеру, чтобы найти дробь для полагаем тогда равенство (6.139) дает

(Для поглощения единиц спереди и сзади в списках параметров мы воспользовались правилом — это правило получается, если подставить

Сравнение (6.135) и (6.139) показывает, что дробь, соответствующая произвольному узлу (6.137) в дереве Штерна—Броко, допускает представление в виде непрерывной дроби

Таким образом, можно без проволочек переходить от непрерывных дробей к соответствующим узлам дерева Штерна—Броко. К примеру,

В гл. 4 мы отмечали, что иррациональные числа определяют бесконечные пути в дереве Штерна—Броко и что они могут быть представлены в виде бесконечной строки букв L и R. Если такой бесконечной строкой для числа является то ей соответствует непрерывная дробь

Подобная бесконечная непрерывная дробь может быть получена и непосредственно. Пусть а при положим

Числа называются „неполными частными" числа Если — рациональное число, скажем то этот процесс перебирает находимые с помощью алгоритма Евклида частные и затем останавливается (при ).

Рациональна или иррациональна эйлерова константа у? Этого никто не знает. Некоторую информацию об этой знаменитой нерешенной проблеме можно получить, поискав число у в дереве Штерна—Броко: если оно рационально, мы найдем его, а если оно иррационально, то мы найдем все наилучшие рациональные приближения к нему. Непрерывная дробь для числа у начинается со следующих неполных частных:

Поэтому представление Штерна—Броко для нее начинается с таких букв никакой очевидной закономерности. Вычисления Ричарда Брента [39] показывают, что если

у — рациональное число, то его знаменатель должен насчитывать более 10 000 десятичных цифр. Поэтому никто не верит в то, что число у рационально, — тем не менее до сих пор никто не смог доказать, что оно таковым не является.

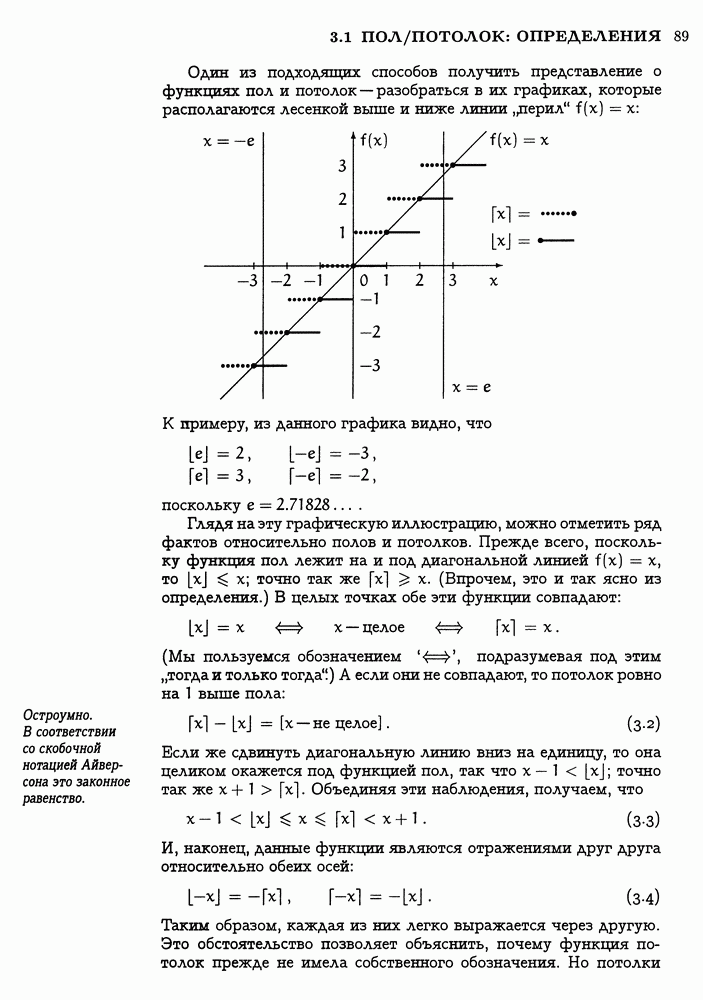
Завершим эту главу доказательством одного замечательного тождества, которое связывает воедино многие из подобных понятий. В гл. 3 было введено понятие спектра — спектром числа называется мультимножество чисел , где а — заданное постоянное число. Поэтому бесконечный ряд

может быть назван производящей функцией для спектра числа , где — отношение золотого сечения. Тождество, которое мы докажем, — открытое в 1976 г. Дж. Л. Дейвисоном [103] — представляет собой бесконечную непрерывную дробь, которая связывает эту производящую функцию с последовательностью Фибоначчи:

Интересны обе части (6.143), но рассмотрим вначале числа . Если фибоначчиево представление (6.113) числа есть , то ожидается, что будет приблизительно равным — числу, которое получается, если сдвинуть фибоначчиево представление влево (как при переводе миль в километры). В действительности из (6.125) известно, что

Поскольку то

и имеет тот же знак, что и — рассуждая аналогично. Следовательно,

Условимся называть число фибоначчиево-нечетным (или, для краткости, - нечетным), если самый младший бит его фибоначчиева представления равен 1 — это все равно, что сказать

. В противном случае число является фибоначчиево-четным (-четным). К примеру, наименьшими -нечетными числами являются 1, 4, 6, 9, 12, 14, 17 и 19. Если четно, то число является -четным в силу (6.114); аналогично, если нечетно, то число является -нечетным. Поэтому

Кроме того, если четно, то из (6.144) следует, что если же нечетно, то (6.144) утверждает, что Таким образом, всегда четно, и доказано, что

Обратно, если — некоторое -четное число, то можно провести это вычисление в обратном порядке и найти такое, что (Сперва прибавляется 1 в -записи, как объяснялось выше. Если переносов не происходит, то число оказывается равным числу сдвинутому вправо; в противном случае число равно сдвинутому вправо Поэтому сумма в правой части (6.143) может быть записана в виде

А как насчет дроби слева? Перепишем чтобы данная непрерывная дробь выглядела как (6.141) — с 1 во всех числителях:

(Это весьма тонкое преобразование! Числитель и знаменатель исходной дроби, имеющей в числителе, нужно поделить на Если оборвать эту новую непрерывную дробь на элементе то ее величина будет равна отношению континуантов

как и в (6.135). Вначале рассмотрим знаменатель, в надежде на его податливость. Полагая находим, что и вообще все продолжается как нельзя лучше и получается геометрический ряд

Соответствующий этому знаменателю числитель оказывается подобным но с меньшим числом членов. К примеру, имеем

в сравнении . Более внимательное рассмотрение выявляет закономерность, определяющую, какие члены присутствуют. Вот она:

и вообще можно доказать по индукции, что

Поэтому

Взяв предел при , получаем (6.146) в силу (6.145).