| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
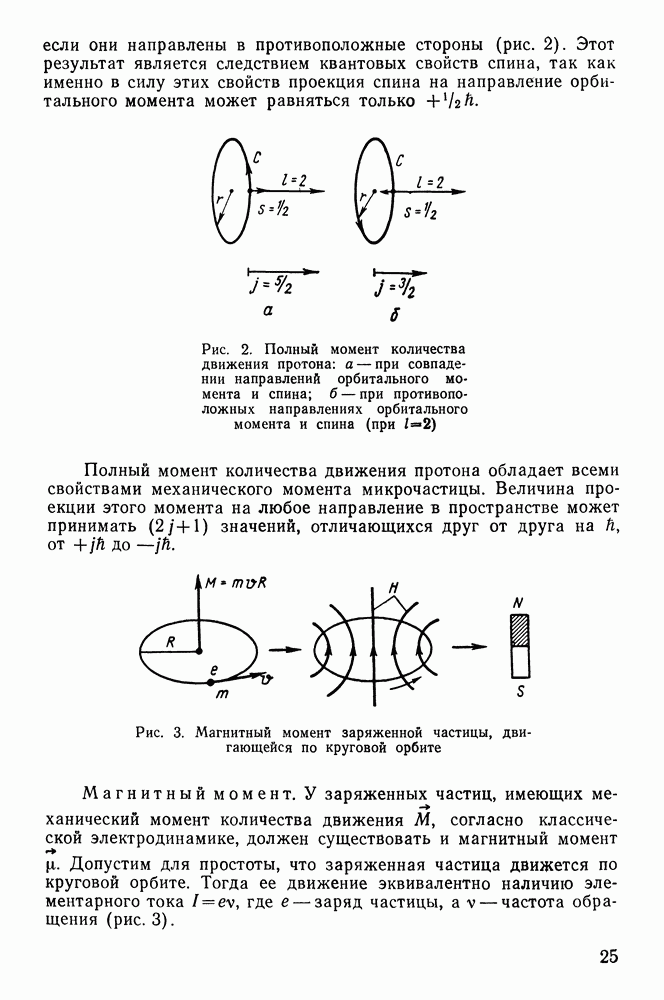
Методы определения спинов и магнитных моментов ядер.
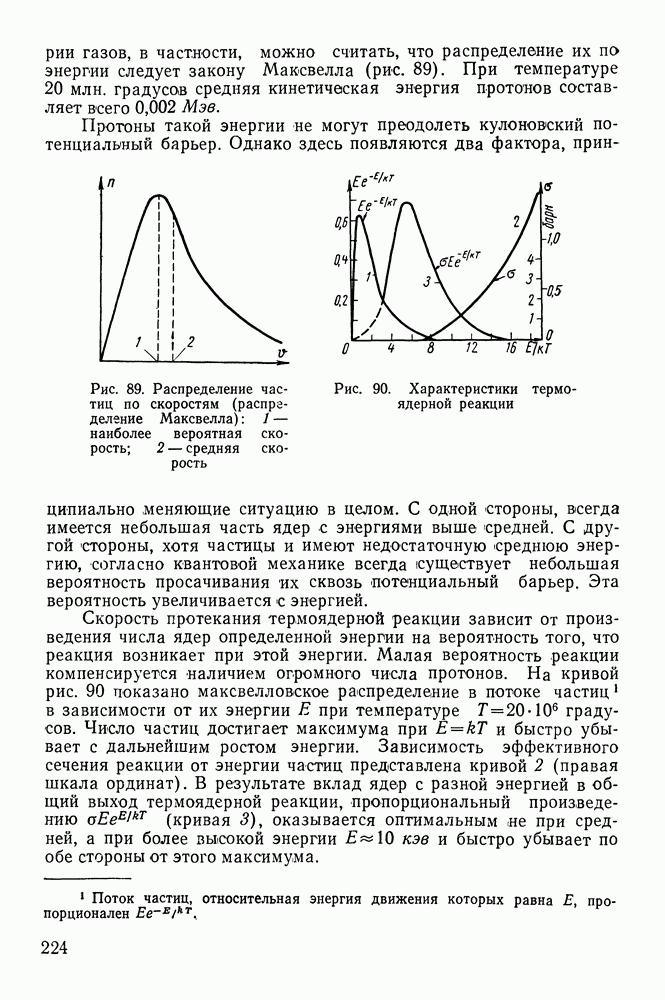
Исследование сверхтонкой структуры атомных спектров. Экспериментально установлено существование тонкой структуры атомных спектральных линий, которая согласно нашим представлениям об атоме возникает из-за взаимодействия магнитного поля, создаваемого орбитальным движением электронов, с магнитным моментом, обусловленным наличием спинов у электронов. Это взаимодействие различно при разных направлениях спина, благодаря чему происходит расщепление линии на две.
Опыт показывает, что линии тонкой структуры, в свою очередь, тоже расщепляются. Это явление получило название сверхтонкой структуры атомных спектров. Объясняется такое расщепление взаимодействием магнитного момента атомного ядра с магнитным полем, создаваемым электронами атомной оболочки. При разных ориентациях спина ядра оно будет различно.
Допустим, что электронная оболочка имеет момент количества движения  а ядро
а ядро  Тогда абсолютное значение полного момента количества движения атома
Тогда абсолютное значение полного момента количества движения атома

где

При данном значении  в зависимости от их ориентации, соответствующая линия может расщепляться на ряд подуровней за счет того, что квантовое число
в зависимости от их ориентации, соответствующая линия может расщепляться на ряд подуровней за счет того, что квантовое число  может принимать несколько значений. При данном
может принимать несколько значений. При данном  число подуровней сразу определит
число подуровней сразу определит 
В месте расположения ядра, имеющего магнитный момент  электронная оболочка создает некоторое среднее магнитное поле
электронная оболочка создает некоторое среднее магнитное поле 
Энергия взаимодействия магнитного момента ядра с магнитным полем электронов будет равна

Пользуясь законами квантовой механики, можно найти значение  выраженное через
выраженное через 

где  - постоянная, определяющая абсолютную величину магнит ного поля электронов. Можно несколькими способами определять спин ядра: подсчитывая число спектральных линий, рассматривая интервалы между линиями, сравнивая их интенсивности [5].
- постоянная, определяющая абсолютную величину магнит ного поля электронов. Можно несколькими способами определять спин ядра: подсчитывая число спектральных линий, рассматривая интервалы между линиями, сравнивая их интенсивности [5].
Спины ядер определяются также из ядерных реакций, так как при превращениях ядер должен сохраняться момент количества движения.
Анализ опытных значений спинов ядер дает возможность сделать ряд важных выводов о структуре ядра в целом и о ядерных силах.
1. При четном А спины всегда целые, при нечетном А спины всегда полуцелые. Как было показано выше, этот факт сыграл решающую роль при переходе от протонно-электронной модели ядра к нейтронно-протонной.
2. Спины всех четно-четных ядер в основных состояниях равны нулю. Это указывает на то, что спины нуклонов одного вида комбинируются так, что момент количества движения пары нуклонов равняется нулю.
3. Спины всех известных ядер не превышают  Отсюда можно предположить, что нуклоны в ядре связаны в замкнутых оболочках и не все участвуют в создании спина ядра.
Отсюда можно предположить, что нуклоны в ядре связаны в замкнутых оболочках и не все участвуют в создании спина ядра.
4. Ядро в состояниях с разными спинами обладает разными энергиями связи. Например, энергия связи дейтона равна  при параллельных спинах. При антипараллельных спинах дейтон в стабильном состоянии вообще не существует. Из этого следует, что ядерные силы зависят от взаимной ориентации спинов.
при параллельных спинах. При антипараллельных спинах дейтон в стабильном состоянии вообще не существует. Из этого следует, что ядерные силы зависят от взаимной ориентации спинов.
Магнитные моменты ядер  также можно довольно грубо определять по сверхтонкой структуре. Однако точность этого метода для определения
также можно довольно грубо определять по сверхтонкой структуре. Однако точность этого метода для определения  очень невелика, поэтому чаще всего определяют магнитные моменты ядер, помещая атомы исследуемого вещества во внешнее магнитное поле.
очень невелика, поэтому чаще всего определяют магнитные моменты ядер, помещая атомы исследуемого вещества во внешнее магнитное поле.
Методы определения спина и магнитного момента ядра, основанные на использовании внешних полей. Если поместить атом во внешнее магнитное поле, то магнитный момент ядра  будет взаимодействовать как с магнитным полем электронов
будет взаимодействовать как с магнитным полем электронов  так и с внешним магнитным полем
так и с внешним магнитным полем  и энергия взаимодействия будет равна:
и энергия взаимодействия будет равна:

Но  поэтому можно написать
поэтому можно написать

В большинстве случаев магнитное взаимодействие между электронной оболочкой и ядром сравнимо по величине со взаимодействием электронных оболочек и ядер с внешним магнитным полем.
Чтобы можно было пренебречь взаимодействием  надо использовать сильные магнитные поля. Здесь следует уточнить, что нужно понимать под «сильным» и «слабым» магнитным полем.
надо использовать сильные магнитные поля. Здесь следует уточнить, что нужно понимать под «сильным» и «слабым» магнитным полем.
Сильным полем  будем называть поле, энергия взаимодействия которого с магнитным моментом электронной оболочки атома
будем называть поле, энергия взаимодействия которого с магнитным моментом электронной оболочки атома  значительно больше энергии взаимодействия поля, создаваемого электронной оболочкой
значительно больше энергии взаимодействия поля, создаваемого электронной оболочкой  с магнитным моментом ядра
с магнитным моментом ядра 

Учитывая, что  получаем для характеристики сильного поля неравенство
получаем для характеристики сильного поля неравенство

Сильное поле как бы разрывает связь между магнитным моментом ядра и магнитным полем электронной оболочки, в результате чего (рис. 9,б) ядерный момент и момент электронной оболочки предессируют вокруг вектора внешнего поля независимо друг от друга в соответствии с собственными моментами  Во внешнем поле получается соответственно
Во внешнем поле получается соответственно  проекций векторов на вектор
проекций векторов на вектор  и столько же значений энергии взаимодействия.
и столько же значений энергии взаимодействия.
В слабом магнитном поле при величине  вокруг вектора внешнего поля прецессирует суммарный вектор
вокруг вектора внешнего поля прецессирует суммарный вектор
атома  который имеет
который имеет  проекций на вектор
проекций на вектор  для каждого из значений
для каждого из значений  Полное число состояний равно
Полное число состояний равно 
Рассмотрим один из наиболее распространенных и наиболее точных методов определения магнитных моментов ядер.

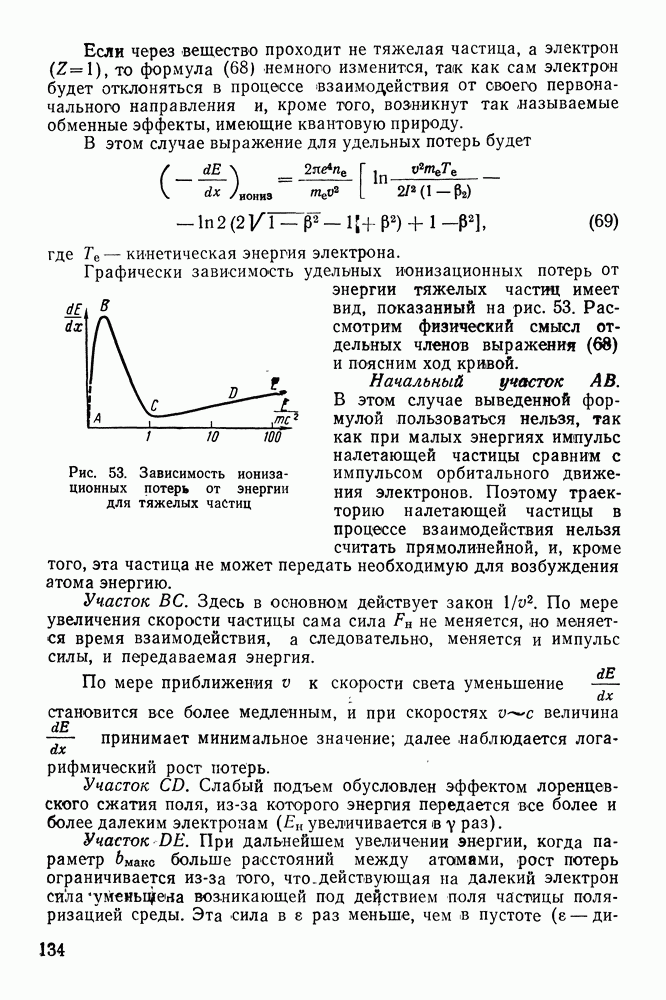
Рис. 9. Прецессия ядерного момента и момента электронной оболочки относительно вектора магнитного поля: а — в слабом внешнем поле; б - в сильном внешнем поле
Метод Раби, или метод магнитного резонанса. Резонансный метод, развитый Раби, дает возможность наблюдать изменение ориентации магнитных моментов атомов, молекул и ядер в постоянном магнитном поле при наличии осциллирующего или вращающегося магнитного поля. При совпадении частоты осциллирующего поля с частотой, определяемой соотношением Бора

( — энергии двух состояний системы в магнитном поле, между которыми возможны магнитные дипольные переходы), происходит резонансная переориентация, сопровождающаяся поглощением или вынужденным испусканием электромагнитной энергии.
— энергии двух состояний системы в магнитном поле, между которыми возможны магнитные дипольные переходы), происходит резонансная переориентация, сопровождающаяся поглощением или вынужденным испусканием электромагнитной энергии.
Правило отбора для таких переходов имеет вид

Первоначально этот метод был использован для изучения молекул, в дальнейшем был проведен ряд экспериментов для исследования ядер, в которых резонанс обнаруживался по  наведенной в процессе переориентации магнитных моментов ядер.
наведенной в процессе переориентации магнитных моментов ядер.
Для иллюстрации рассмотрим магнитный резонансный метод в применении к молекулярным или атомным пучкам.
Установка, на которой проводится исследование, состоит из трех электромагнитов  создающих три постоянных магнитных поля
создающих три постоянных магнитных поля  причем в вертикальной плоскости, проходящей через ось системы, они все направлены одинаково, например вверх — по оси
причем в вертикальной плоскости, проходящей через ось системы, они все направлены одинаково, например вверх — по оси  (рис. 10).
(рис. 10).
Источник О посылает вдоль оси системы пучок частиц, на пути которых помещена диафрагма  На конце системы приемник
На конце системы приемник  измеряет интенсивность потока частиц. Поля
измеряет интенсивность потока частиц. Поля  сильно неоднородны, одинаковы по своей величине, но направления
сильно неоднородны, одинаковы по своей величине, но направления
градиентов полей  у них противоположны. Поле
у них противоположны. Поле  однородно, т. е.
однородно, т. е.


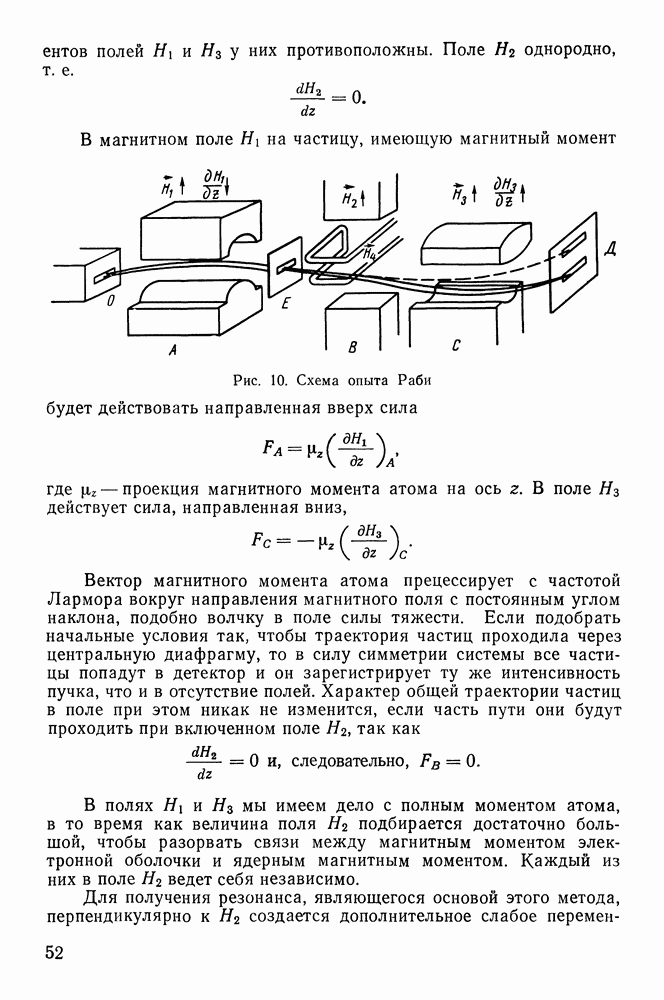
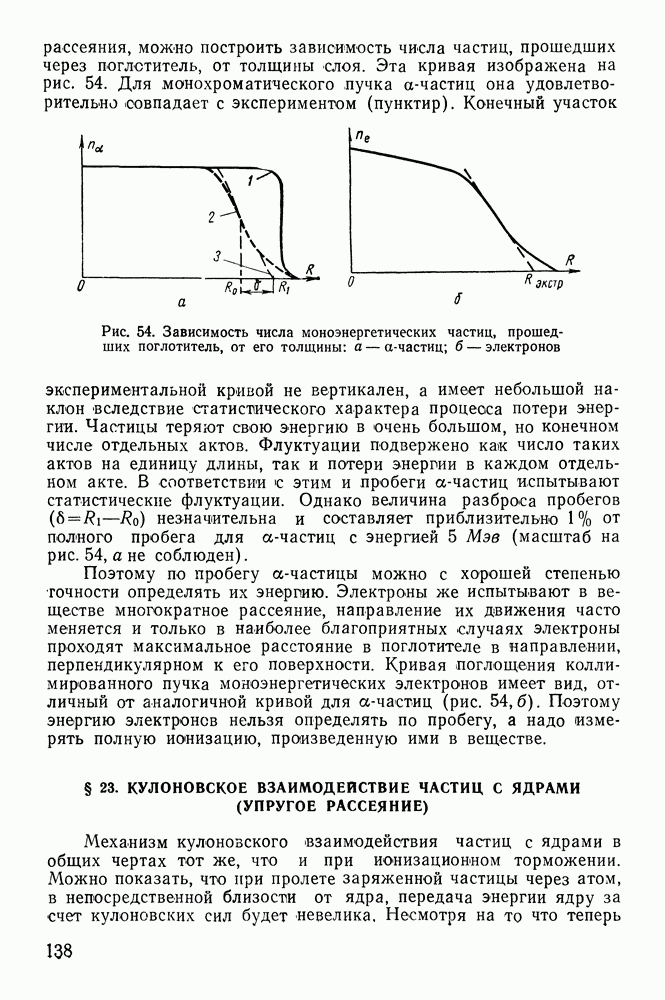
Рис. 10. Схема опыта Раби
В магнитном поле  на частицу, имеющую магнитный момент будет действовать направленная вверх сила
на частицу, имеющую магнитный момент будет действовать направленная вверх сила

где  проекция магнитного момента атома на ось
проекция магнитного момента атома на ось  В поле
В поле  действует сила, направленная вниз,
действует сила, направленная вниз,

Вектор магнитного момента атома прецессирует с частотой Лармора вокруг направления магнитного поля с постоянным углом наклона, подобно волчку в поле силы тяжести. Если подобрать начальные условия так, чтобы траектория частиц проходила через центральную диафрагму, то в силу симметрии системы все частицы попадут в детектор и он зарегистрирует ту же интенсивность пучка, что и в отсутствие полей. Характер общей траектории частиц в поле при этом никак не изменится, если часть пути они будут проходить при включенном поле  так как
так как

В полях  мы имеем дело с полным моментом атома, в то время как величина поля
мы имеем дело с полным моментом атома, в то время как величина поля  подбирается достаточно большой, чтобы разорвать связи между магнитным моментом электронной оболочки и ядерным магнитным моментом. Каждый из них в поле
подбирается достаточно большой, чтобы разорвать связи между магнитным моментом электронной оболочки и ядерным магнитным моментом. Каждый из них в поле  ведет себя независимо.
ведет себя независимо.
Для получения резонанса, являющегося основой этого метода, перпендикулярно к  создается дополнительное слабое
создается дополнительное слабое
переменное поле  с частотой
с частотой  Четвертое поле будет вызывать поворот ядерного волчка, увеличивая или уменьшая угол между его осью и направлением ноля (рис. 11) и тем самым изменяя проекцию ядерного момента на ось
Четвертое поле будет вызывать поворот ядерного волчка, увеличивая или уменьшая угол между его осью и направлением ноля (рис. 11) и тем самым изменяя проекцию ядерного момента на ось  Действительно, осциллирующее поле можно заменить двумя циклическими полями, одно из которых вращается навстречу лармовой прецессии и ничего не меняет, а второе, вращающееся в сторону прецессии, увеличивает или уменьшает угол
Действительно, осциллирующее поле можно заменить двумя циклическими полями, одно из которых вращается навстречу лармовой прецессии и ничего не меняет, а второе, вращающееся в сторону прецессии, увеличивает или уменьшает угол  .
.

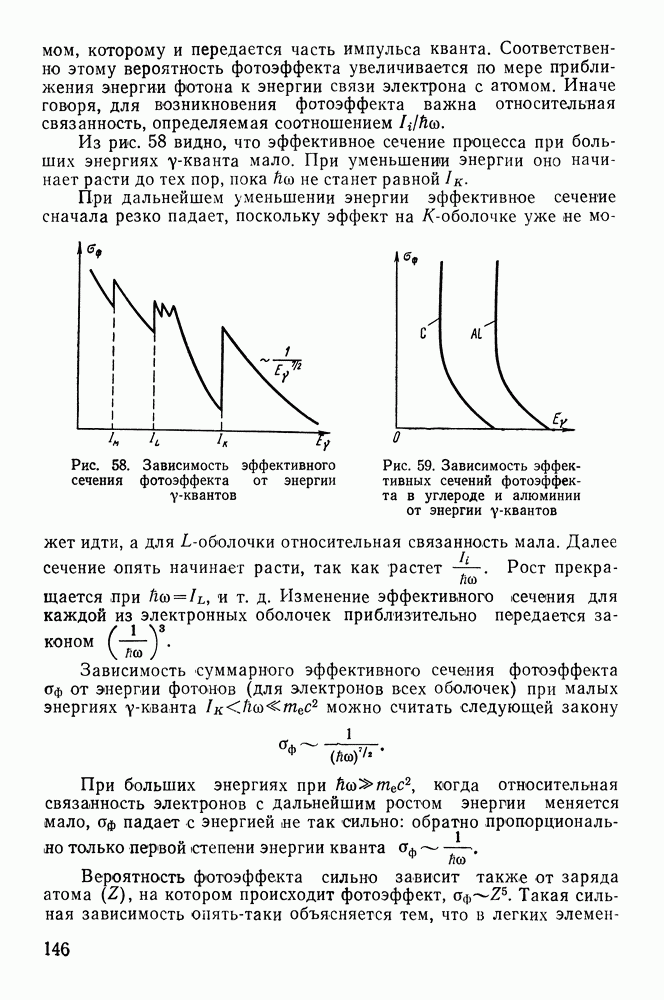
Рис. 11. Влияние вращающегося магнитного поля  на угол между вектором результирующего магнитного момента и вектором магнитного поля Н
на угол между вектором результирующего магнитного момента и вектором магнитного поля Н
При частоте этого поля, совпадающий с лармовой частотой прецессии ядра  происходит резонансная переориентация ядерных магнитных диполей относительно направления постоянного магнитного поля.
происходит резонансная переориентация ядерных магнитных диполей относительно направления постоянного магнитного поля.
Энергия, которая необходима для переориентации диполей

заимствуется у высокочастотного поля (поглощается электромагнитный квант соответствующей частоты).
Энергия взаимодействия сильного поля  с ядерным магнитным моментом
с ядерным магнитным моментом  равна
равна

Изменение этой энергии при переходе

(переходы разрешены при  ). При этих условиях частота перехода
). При этих условиях частота перехода

Но согласно соотношению (23)

поэтому

или для циклической частоты получаем окончательно

В результате переориентировки магнитных моментов при частоте поля  равной
равной  угол
угол  за время пролета частицей поля
за время пролета частицей поля  успеет заметно измениться.
успеет заметно измениться.

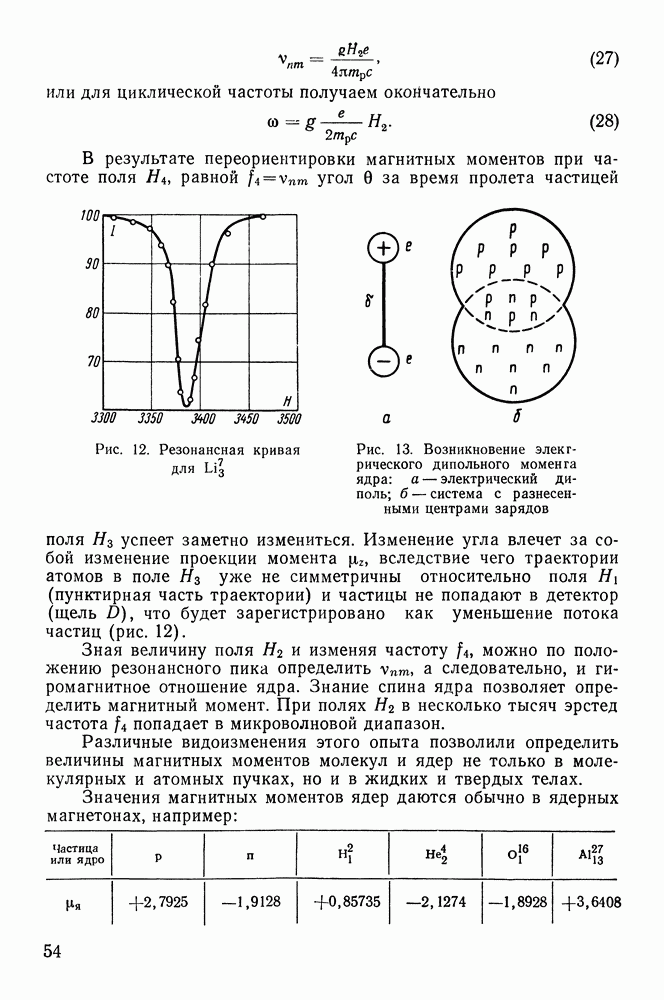
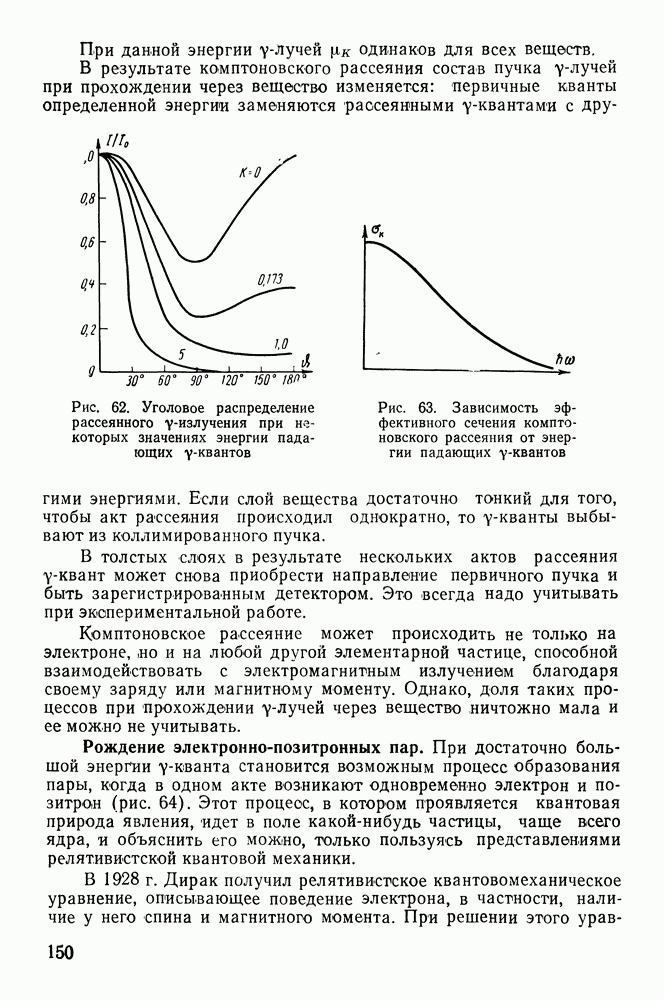
Рис. 12. Резонансная кривая для 

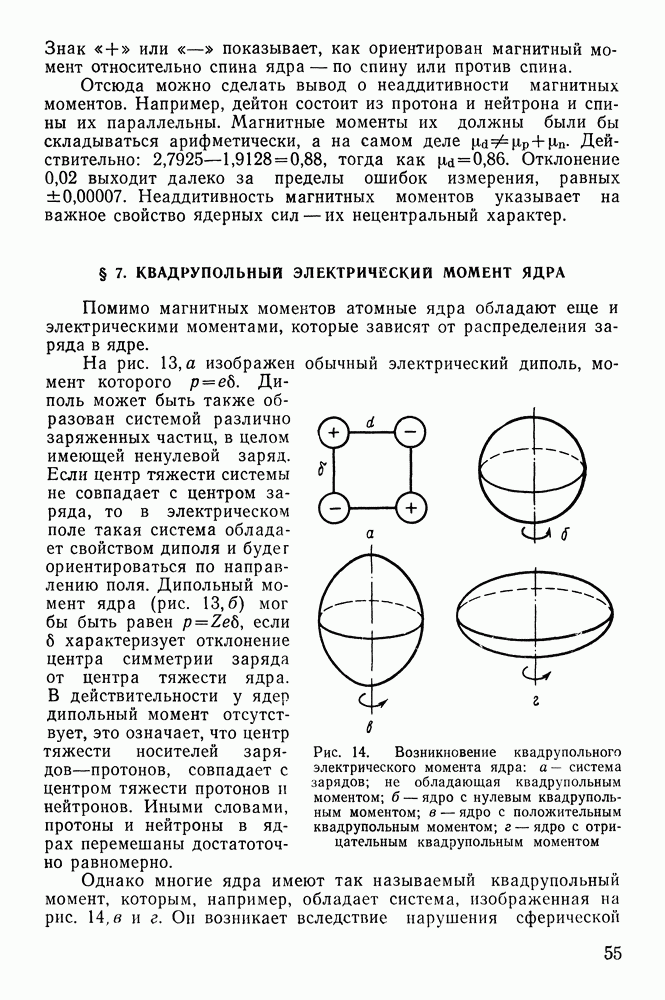
Рис. 13. Возникновение электрического дипольного момента ядра: а — электрический диполь;  система с разнесенными центрами зарядов
система с разнесенными центрами зарядов
Изменение угла влечет за собой изменение проекции момента  вследствие чего траектории атомов в поле
вследствие чего траектории атомов в поле  уже не симметричны относительно поля
уже не симметричны относительно поля  (пунктирная часть траектории) и частицы не попадают в детектор (щель D), что будет зарегистрировано как уменьшение потока частиц (рис. 12).
(пунктирная часть траектории) и частицы не попадают в детектор (щель D), что будет зарегистрировано как уменьшение потока частиц (рис. 12).
Зная величину поля  и изменяя частоту
и изменяя частоту  можно по положению резонансного пика определить
можно по положению резонансного пика определить  а следовательно, и гиромагнитное отношение ядра. Знание спина ядра позволяет определить магнитный момент. При полях
а следовательно, и гиромагнитное отношение ядра. Знание спина ядра позволяет определить магнитный момент. При полях  в несколько тысяч эрстед частота
в несколько тысяч эрстед частота  попадает в микроволновой диапазон.
попадает в микроволновой диапазон.
Различные видоизменения этого опыта позволили определить величины магнитных моментов молекул и ядер не только в молекулярных и атомных пучках, но и в жидких и твердых телах.
Значения магнитных моментов ядер даются обычно в ядерных магнетонах, например:
(см. скан)
Знак  или
или  показывает, как ориентирован магнитный момент относительно спина ядра — по спину или против спина.
показывает, как ориентирован магнитный момент относительно спина ядра — по спину или против спина.
Отсюда можно сделать вывод о неаддитивности магнитных моментов. Например, дейтон состоит из протона и нейтрона и спины их параллельны. Магнитные моменты их должны были бы складываться арифметически, а на самом деле  Действительно:
Действительно:  тогда как
тогда как  Отклонение 0,02 выходит далеко за пределы ошибок измерения, равных
Отклонение 0,02 выходит далеко за пределы ошибок измерения, равных  . Неаддитивность магнитных моментов указывает на важное свойство ядерных сил — их нецентральный характер.
. Неаддитивность магнитных моментов указывает на важное свойство ядерных сил — их нецентральный характер.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Масштабы физических величин.
- Особенности физических явлений в микромире.
- РАЗДЕЛ ПЕРВЫЙ. СТАБИЛЬНЫЕ ЯДРА И ЯДЕРНЫЕ СИЛЫ
- § 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ПРОТОНА И НЕЙТРОНА
- § 2. ЗАРЯД АТОМНОГО ЯДРА
- § 3. РАЗМЕРЫ АТОМНЫХ ЯДЕР
- § 4. ЭНЕРГИЯ СВЯЗИ ЯДРА
- § 5. МАССА И ЭНЕРГИЯ
- § 6. СПИН И МАГНИТНЫЙ МОМЕНТ ЯДРА
- Методы определения спинов и магнитных моментов ядер.
- § 7. КВАДРУПОЛЬНЫЙ ЭЛЕКТРИЧЕСКИЙ МОМЕНТ ЯДРА
- § 8. ЧЕТНОСТЬ ВОЛНОВОЙ ФУНКЦИИ
- § 9. ЯДЕРНЫЕ МОДЕЛИ
- Глава вторая. ЯДЕРНЫЕ СИЛЫ
- § 10. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДЕРНЫХ СИЛ
- § 11. ФИЗИЧЕСКИЕ ОБОСНОВАНИЯ МЕЗОННОИ ТЕОРИИ ЯДЕРНЫХ СИЛ
- § 12. СТРУКТУРА НУКЛОНА
- § 13. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДЕЙТОНА
- Магнитный момент дейтона.
- РАЗДЕЛ ВТОРОЙ. НЕУСТОЙЧИВЫЕ ЯДРА
- § 14. ОТКРЫТИЕ РАДИОАКТИВНОСТИ
- § 15. ЗАКОНЫ РАДИОАКТИВНОГО РАСПАДА
- § 16. ТРАНСУРАНОВЫЕ ЭЛЕМЕНТЫ
- § 17. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ ИЗОТОПОВ
- § 18. АЛЬФА-РАСПАД
- § 19. БЕТА-РАСПАД
- Энергетические спектры электронов при b-распаде и роль нейтрино.
- Энергетические соотношения при b-распаде.
- § 20. ГАММА-ИЗЛУЧЕНИЕ ЯДЕР
- Ядерная изомерия.
- Эффект Мёссбауера.
- ГЛАВА ЧЕТВЕРТАЯ. ВЗАИМОДЕЙСТВИЕ ЯДЕРНОГО ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
- § 21. ВИДЫ ВЗАИМОДЕЙСТВИЯ
- § 22. ВЗАИМОДЕЙСТВИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ СО СРЕДОЙ
- Пробег заряженных частиц в веществе.
- § 23. КУЛОНОВСКОЕ ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ С ЯДРАМИ (УПРУГОЕ РАССЕЯНИЕ)
- § 24. ЯДЕРНОЕ ВЗАИМОДЕЙСТВИЕ
- § 25. ИЗЛУЧЕНИЕ ВАВИЛОВА — ЧЕРЕНКОВА
- § 26. ПРОХОЖДЕНИЕ ГАММА-ИЗЛУЧЕНИЯ ЧЕРЕЗ ВЕЩЕСТВО
- Рассеяние y-лучей. Эффект Комптона.
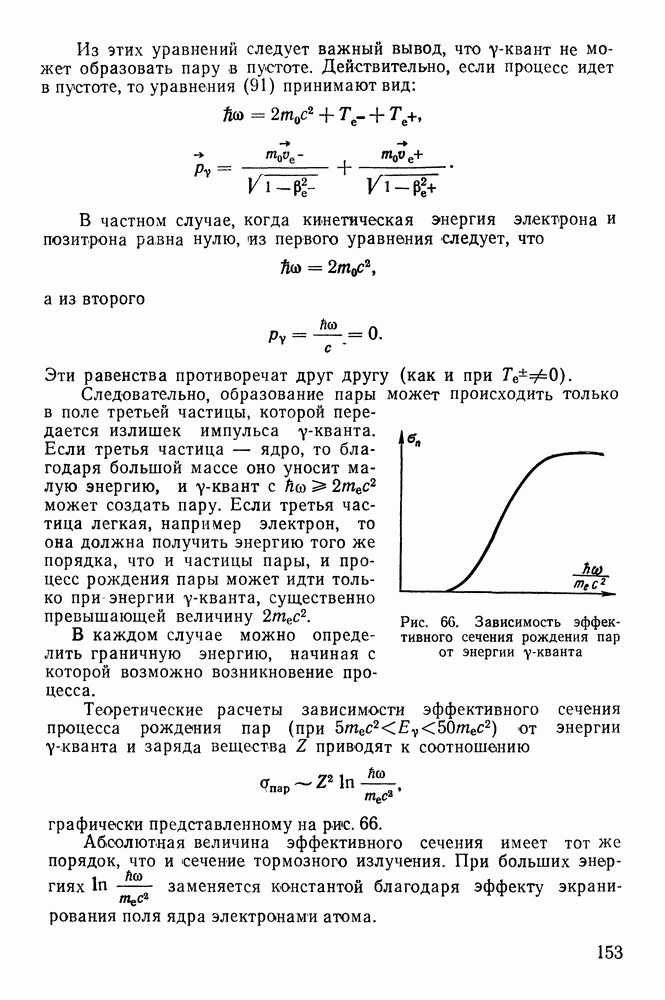
- Рождение электронно-позитронных пар.
- Другие эффекты, возникающие при поглощении y-лучей
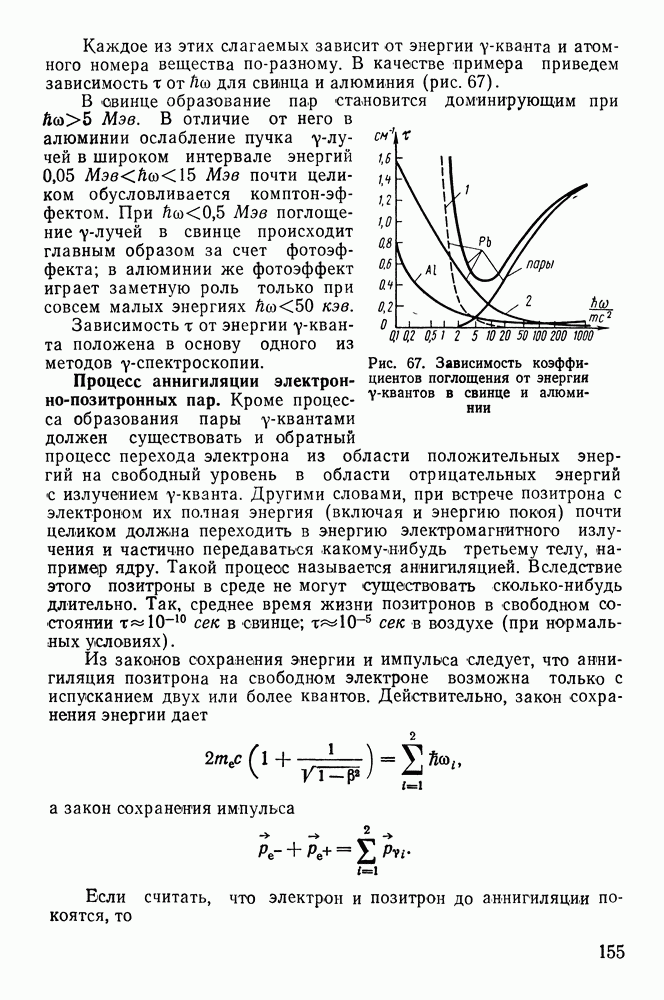
- Суммарный коэффициент поглощения y-излучения
- Процесс аннигиляции электронно-позитронных пар.
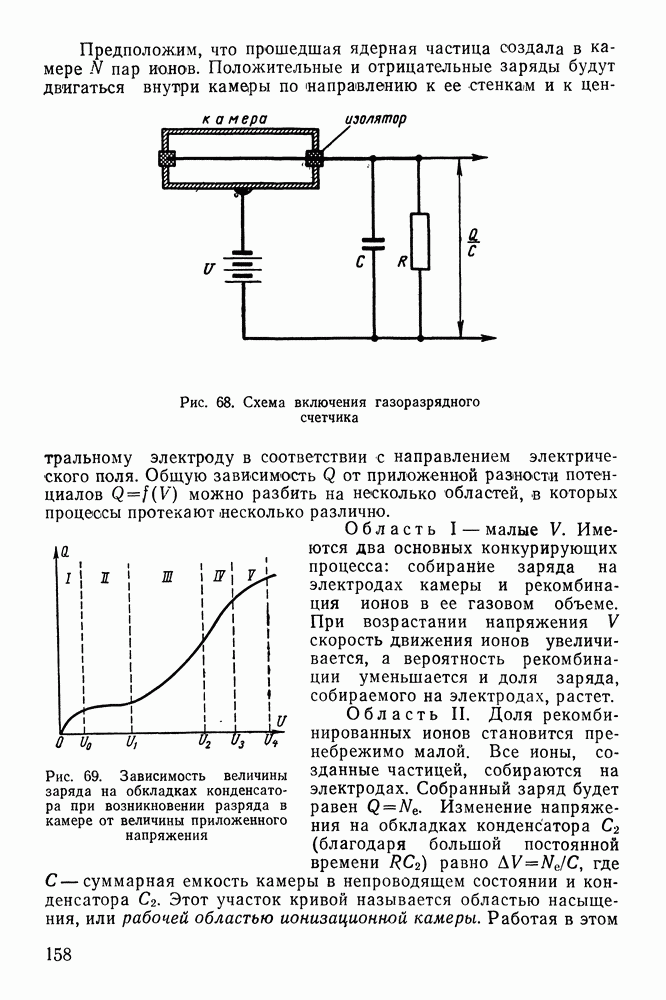
- § 27. МЕТОДЫ РЕГИСТРАЦИИ ИЗЛУЧЕНИЯ
- РАЗДЕЛ ТРЕТИЙ. ЯДЕРНЫЕ РЕАКЦИИ
- ГЛАВА ПЯТАЯ. ЗАКОНОМЕРНОСТИ ЯДЕРНЫХ РЕАКЦИЙ
- § 29. ЗАКОНЫ СОХРАНЕНИЯ В ЯДЕРНЫХ РЕАКЦИЯХ
- § 30. РАЗЛИЧНЫЕ МЕХАНИЗМЫ РЕАКЦИЙ
- ГЛАВА ШЕСТАЯ. ФИЗИКА НЕЙТРОНОВ
- § 31. ОТКРЫТИЕ НЕЙТРОНА И ЕГО СВОЙСТВА
- § 32. ИСТОЧНИКИ НЕЙТРОНОВ
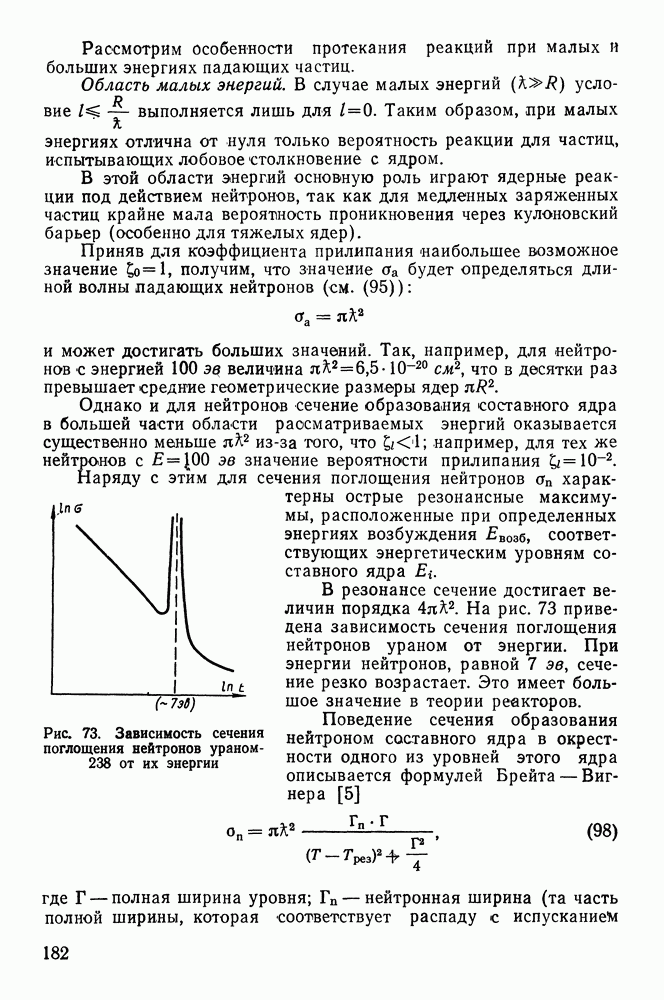
- § 33. ВЗАИМОДЕЙСТВИЕ НЕЙТРОНОВ С ВЕЩЕСТВОМ
- § 34. МЕТОДЫ РЕГИСТРАЦИИ НЕЙТРОНОВ
- § 35. ЗАМЕДЛЕНИЕ НЕЙТРОНОВ
- § 36. МЕТОДЫ ПОЛУЧЕНИЯ МОНОХРОМАТИЧЕСКИХ НЕЙТРОНОВ
- ГЛАВА СЕДЬМАЯ. ДЕЛЕНИЕ И СИНТЕЗ ЯДЕР
- § 37. ОТКРЫТИЕ ДЕЛЕНИЯ ЯДЕР
- § 38. ПРОЦЕССЫ, ПРОИСХОДЯЩИЕ ПРИ ДЕЛЕНИИ ЯДЕР УРАНА
- § 39. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДЕЛЕНИЯ
- § 40. ТИПЫ РЕАКЦИЙ ДЕЛЕНИЯ
- § 41. ВОЗМОЖНОСТЬ ИСПОЛЬЗОВАНИЯ ЯДЕРНОЙ ЭНЕРГИИ
- § 42. ЦЕПНАЯ ЯДЕРНАЯ РЕАКЦИЯ И ЯДЕРНЫЕ РЕАКТОРЫ
- § 43. ТЕРМОЯДЕРНЫЙ СИНТЕЗ
- Термоядерные реакции в лабораторных условиях.
- РАЗДЕЛ ЧЕТВЕРТЫЙ. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И КОСМИЧЕСКИЕ ЛУЧИ
- § 44. ОТКРЫТИЕ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
- § 45. ВИДЫ ВЗАИМОДЕЙСТВИЯ ЧАСТИЦ
- § 46. КЛАССИФИКАЦИЯ ЧАСТИЦ
- § 47. РЕАКЦИИ МЕЖДУ ЧАСТИЦАМИ
- § 48. ВНУТРЕННИЕ СВОЙСТВА ЧАСТИЦ
- § 49. РЕЗОНАНСЫ
- § 50. ПОПЫТКИ СИСТЕМАТИЗАЦИИ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
- § 51. ГИПЕРФРАГМЕНТЫ (ИЛИ Л°-ЯДРА)
- § 52. НАРУШЕНИЕ ЗАКОНА СОХРАНЕНИЯ ЧЕТНОСТИ
- § 53. ФИЗИКА НЕЙТРИНО
- ГЛАВА ДЕВЯТАЯ. КОСМИЧЕСКИЕ ЛУЧИ
- § 54. ОТКРЫТИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- § 55. ПЕРВИЧНОЕ ИЗЛУЧЕНИЕ У ЗЕМЛИ
- § 56. ВЗАИМОДЕЙСТВИЕ КОСМИЧЕСКОГО ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
- § 57. СОСТАВ КОСМИЧЕСКИХ ЛУЧЕЙ НА УРОВНЕ МОРЯ
- § 58. ВРЕМЕННЫЕ ИЗМЕНЕНИЯ ИНТЕНСИВНОСТИ КОСМИЧЕСКИХ ЛУЧЕЙ
- § 59. РАДИАЦИОННЫЕ ПОЯСА
- § 60. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА