| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 15. ЗАКОНЫ РАДИОАКТИВНОГО РАСПАДА
Изменение числа радиоактивных ядер во времени. Резерфорд и Содди в 1911 г., обобщая экспериментальные результаты, показали, что атомы некоторых элементов испытывают последовательные превращения, образуя радиоактивные семейства, где каждый член возникает из предыдущего и, в свою очередь, образует последующий.
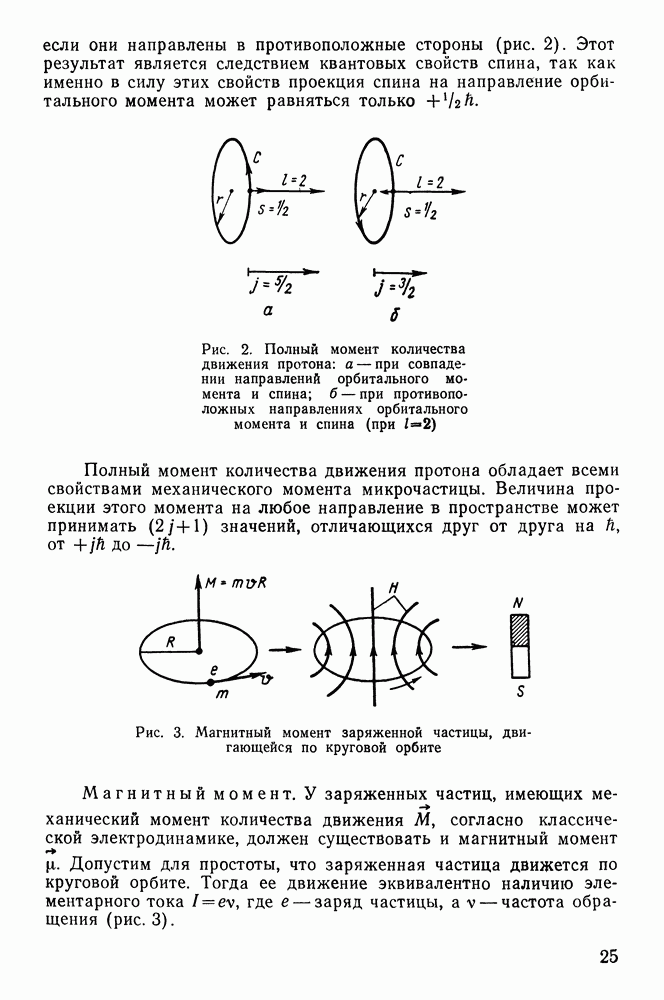
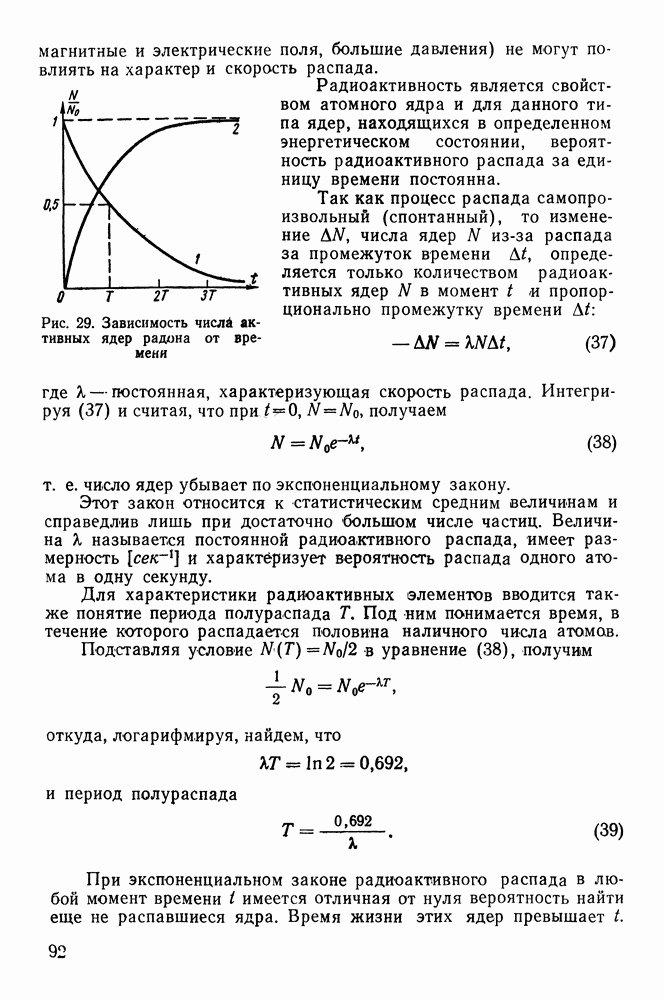
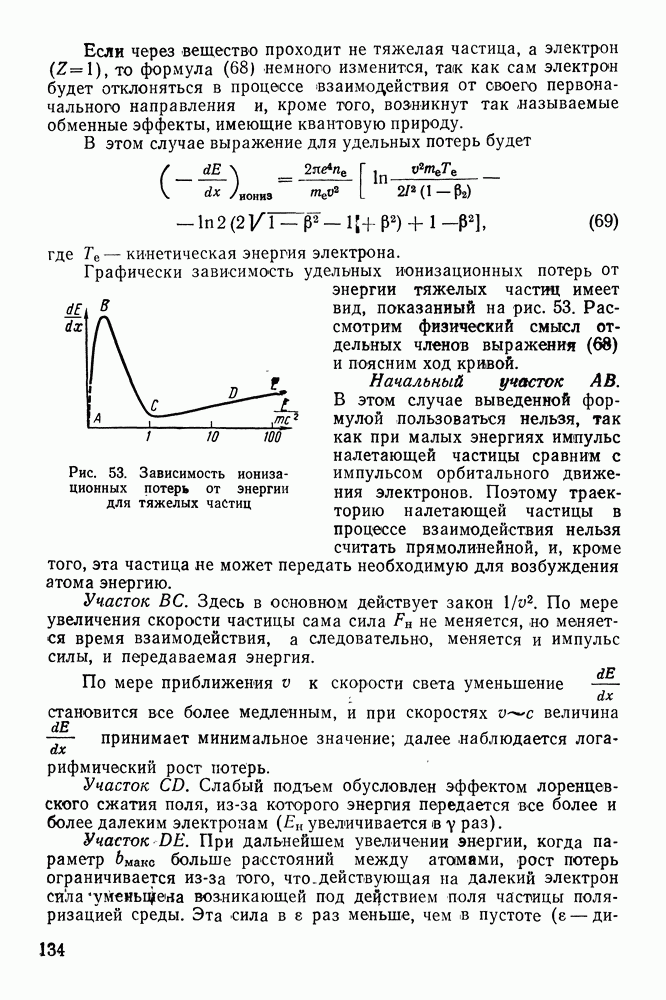
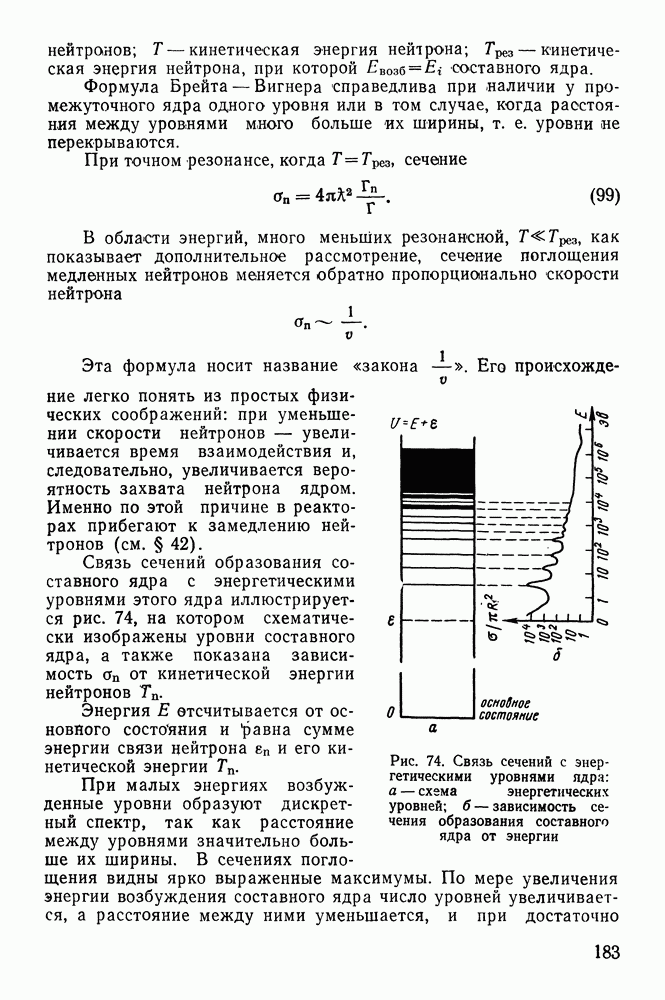
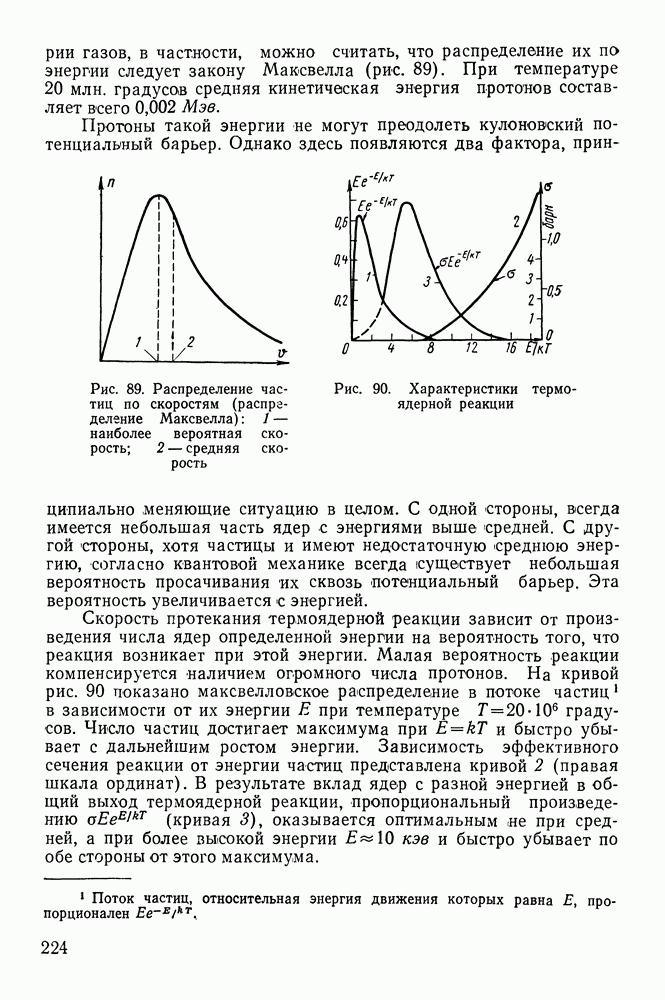
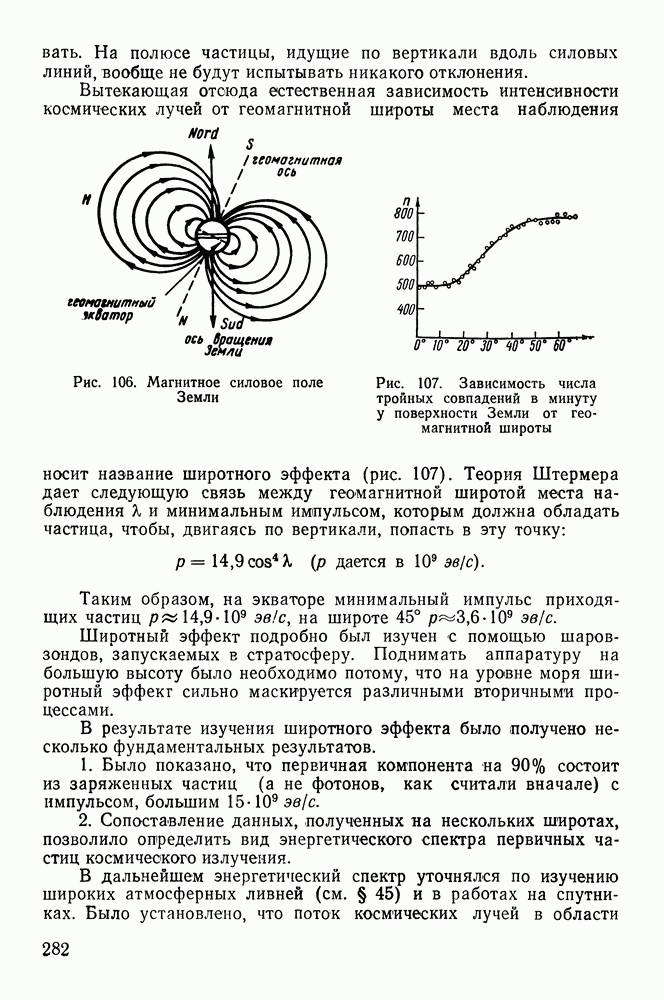
Это удобно проиллюстрировать на примере образования радона из радия. Если поместить в запаянную ампулу  то анализ газа через несколько дней покажет, что в нем появляется гелий и радон. Гелий устойчив, и поэтому он накапливается, радон же сам распадается. Кривая 1 на рис. 29 характеризует закон распада радона в отсутствие радия. При этом на оси ординат отложено отношение числа нераспавшихся ядер радона
то анализ газа через несколько дней покажет, что в нем появляется гелий и радон. Гелий устойчив, и поэтому он накапливается, радон же сам распадается. Кривая 1 на рис. 29 характеризует закон распада радона в отсутствие радия. При этом на оси ординат отложено отношение числа нераспавшихся ядер радона  к их начальному числу
к их начальному числу  Видно, что убывание содержания
Видно, что убывание содержания  идет по экспоненциальному закону. Кривая 2 показывает, как изменяется число радиоактивных ядер радона в присутствии радия.
идет по экспоненциальному закону. Кривая 2 показывает, как изменяется число радиоактивных ядер радона в присутствии радия.
Опыты, проведенные с радиоактивными веществами, показали, что никакие внешние условия (нагревание до высоких температур,
магнитные и электрические поля, большие давления) не могут повлиять на характер и скорость распада.
Радиоактивность является свойством атомного ядра и для данного типа ядер, находящихся в определенном энергетическом состоянии, вероятность радиоактивного распада за единицу времени постоянна.

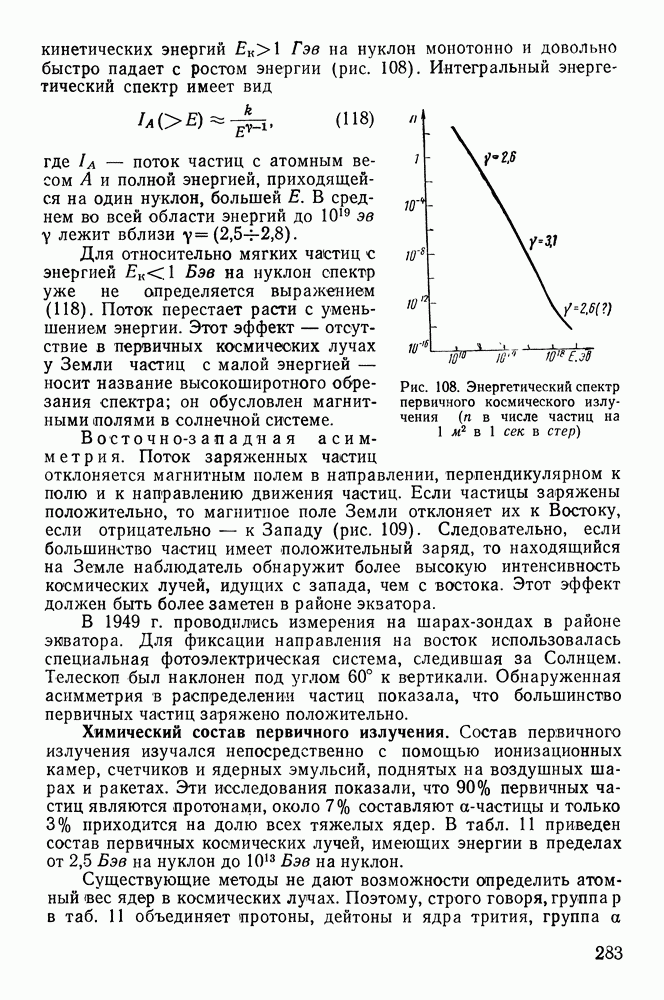
Рис. 29. Зависимость числа активных ядер радона от времени
Так как процесс распада самопроизвольный (спонтанный), то изменение  числа ядер
числа ядер  из-за распада за промежуток времени
из-за распада за промежуток времени  определяется только количеством радиоактивных ядер
определяется только количеством радиоактивных ядер  в момент
в момент  и пропорционально промежутку времени
и пропорционально промежутку времени 

где  постоянная, характеризующая скорость распада. Интегрируя (37) и считая, что
постоянная, характеризующая скорость распада. Интегрируя (37) и считая, что  получаем
получаем

т. е. число ядер убывает по экспоненциальному закону.
Этот закон относится к статистическим средним величинам и справедлив лишь при достаточно большом числе частиц. Величина X называется постоянной радиоактивного распада, имеет размерность  и характеризует вероятность распада одного атома в одну секунду.
и характеризует вероятность распада одного атома в одну секунду.
Для характеристики радиоактивных элементов вводится также понятие периода полураспада  Под ним понимается время, в течение которого распадается половина наличного числа атомов. Подставляя условие
Под ним понимается время, в течение которого распадается половина наличного числа атомов. Подставляя условие  в уравнение (38), получим
в уравнение (38), получим

откуда, логарифмируя, найдем, что

и период полураспада

При экспоненциальном законе радиоактивного распада в любой момент времени  имеется отличная от нуля вероятность найти еще не распавшиеся ядра. Время жизни этих ядер превышает
имеется отличная от нуля вероятность найти еще не распавшиеся ядра. Время жизни этих ядер превышает 
Наоборот, другие ядра, распавшиеся к этому времени, прожили разное время, меньшее  Среднее время жизни для данного радиоактивного изотопа определяется как
Среднее время жизни для данного радиоактивного изотопа определяется как

Обозначив  получим
получим

откуда

Следовательно, среднее время жизни  радиоактивного ядра равно обратной величине от постоянной распада Я. За время
радиоактивного ядра равно обратной величине от постоянной распада Я. За время  первоначальное число ядер уменьшается в
первоначальное число ядер уменьшается в  раз.
раз.
Для обработки экспериментальных результатов удобно представить уравнение (38) в другой форме:

Величина  называется активностью данного радиоактивного препарата, она определяет число распадов в секунду. Активность является характеристикой всего распадающегося вещества, а не отдельного ядра. Практической единицей активности является кюри. 1 кюри
называется активностью данного радиоактивного препарата, она определяет число распадов в секунду. Активность является характеристикой всего распадающегося вещества, а не отдельного ядра. Практической единицей активности является кюри. 1 кюри  равно ислу распавшихся ядер содержащихся в
равно ислу распавшихся ядер содержащихся в  радия за 1 сек
радия за 1 сек  распадов/сек). Используются и более мелкие единицы — милликюри
распадов/сек). Используются и более мелкие единицы — милликюри  и микрокюри
и микрокюри  . В практике физического эксперимента используется иногда другая единица активности — Резерфорд
. В практике физического эксперимента используется иногда другая единица активности — Резерфорд  распадов/сек.
распадов/сек.
Статистический характер радиоактивного распада. Радиоактивный распад — явление принципиально статистическое. Мы не можем сказать, когда именно распадется данное ядро, а можем лишь указать, с какой вероятностью оно распадается за тот или иной промежуток времени.
Радиоактивные ядра не «стареют» в процессе своего существования. К ним вообще неприменимо понятие возраста, а можно лишь говорить о среднем времени их жизни.
Из статистического характера закона радиоактивного распада следует, что он выполняется строго, когда  велико, а при небольших
велико, а при небольших  должны наблюдаться флуктуации. Число распадающихся ядер в единицу времени должно флуктуировать вокруг среднего значения, харак теризуемого приведенным выше законом. Это подтверждается экспериментальными измерениями числа
должны наблюдаться флуктуации. Число распадающихся ядер в единицу времени должно флуктуировать вокруг среднего значения, харак теризуемого приведенным выше законом. Это подтверждается экспериментальными измерениями числа  -частиц, испускаемых радиоактивным веществом в единицу времени.
-частиц, испускаемых радиоактивным веществом в единицу времени.

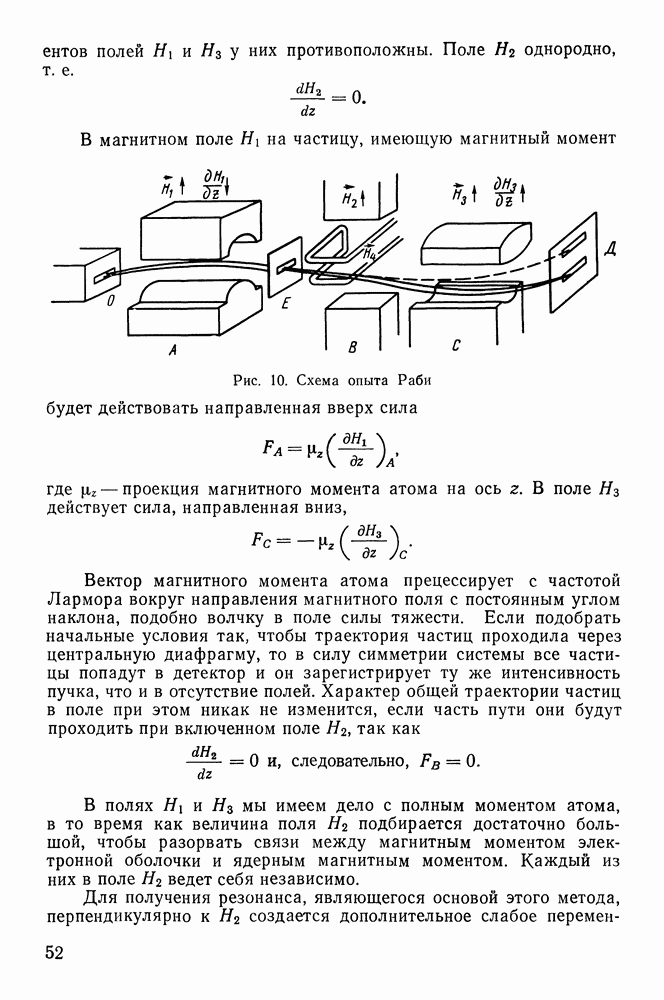
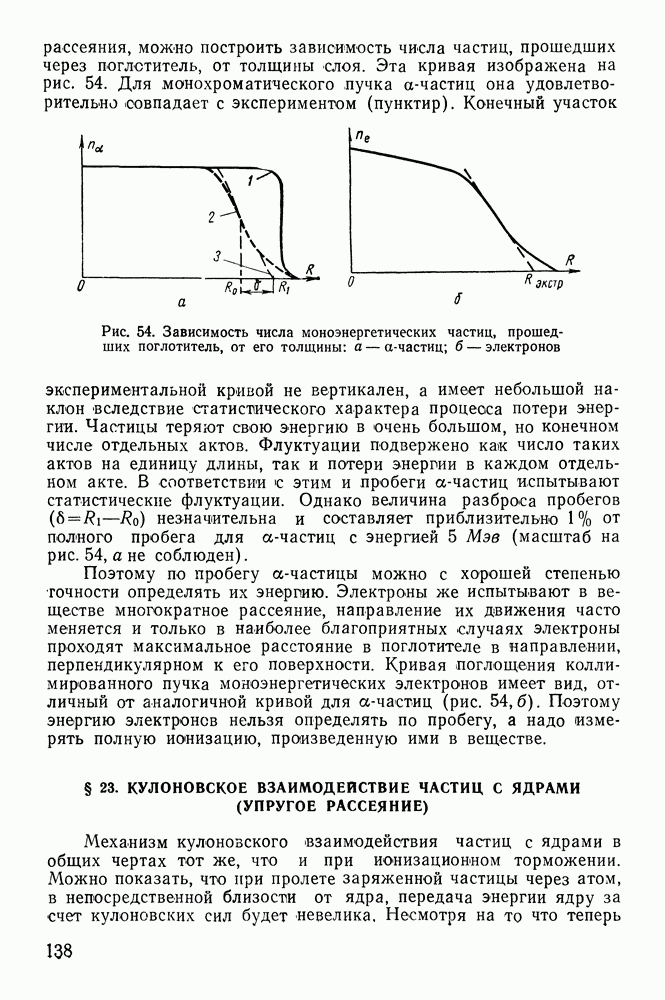
Рис. 30. Зависимость логарифма активности от времени
Флуктуации подчиняются закону Пуассона. Производя измерения с радиоактивными препаратами, надо всегда это учитывать и определять статистическую точность опытных результатов.
Определение постоянной распада X. При определении постоянной распада X радиоактивного элемента опыт сводится к регистрации числа частиц, вылетающих из препарата за единицу времени, т. е. определяется его активность  Затем строится график изменения активности со временем, обычно в полулогарифмическом масштабе. Вид получаемых зависимостей при исследованиях чистого изотопа, смеси изотопов или радиоактивного семейства оказывается различным.
Затем строится график изменения активности со временем, обычно в полулогарифмическом масштабе. Вид получаемых зависимостей при исследованиях чистого изотопа, смеси изотопов или радиоактивного семейства оказывается различным.
Рассмотрим в качестве примера несколько случаев.
1. Исследуется один радиоактивный элемент, при распаде которого образуются стабильные ядра. Логарифмируя выражение (41), получим

Следовательно, в этом случае логарифм активности является линейной функцией времени. График этой зависимости имеет вид прямой, тангенс угла наклона которой (рис. 30) 
2. Исследуется радиоактивное семейство, в котором происходит целая цепь радиоактивных превращений. Ядра, получающиеся после распада, в свою очередь сами оказываются радиоактивными:

Примером такой цепочки может служить распад:


Найдем закон, описывающий в этом случае изменение числа радиоактивных атомов во времени. Для простоты выделим всего два элемента:  считая А исходным, а В промежуточным.
считая А исходным, а В промежуточным.
Тогда изменение числа ядер А и ядер В определится из системы уравнений

Количество ядер А убывает за счет их распада, а количество ядер В убывает из-за распада ядер В и возрастает за счет распада ядер А.
Если при  имеется
имеется  ядер А, а ядер В нет, то начальные условия запишутся в виде
ядер А, а ядер В нет, то начальные условия запишутся в виде

Решение уравнений (43) имеет вид

и полная активность источника, состоящего из ядер А и В:

Рассмотрим теперь зависимость логарифма радиоактивности от времени при разных соотношениях между  и
и 
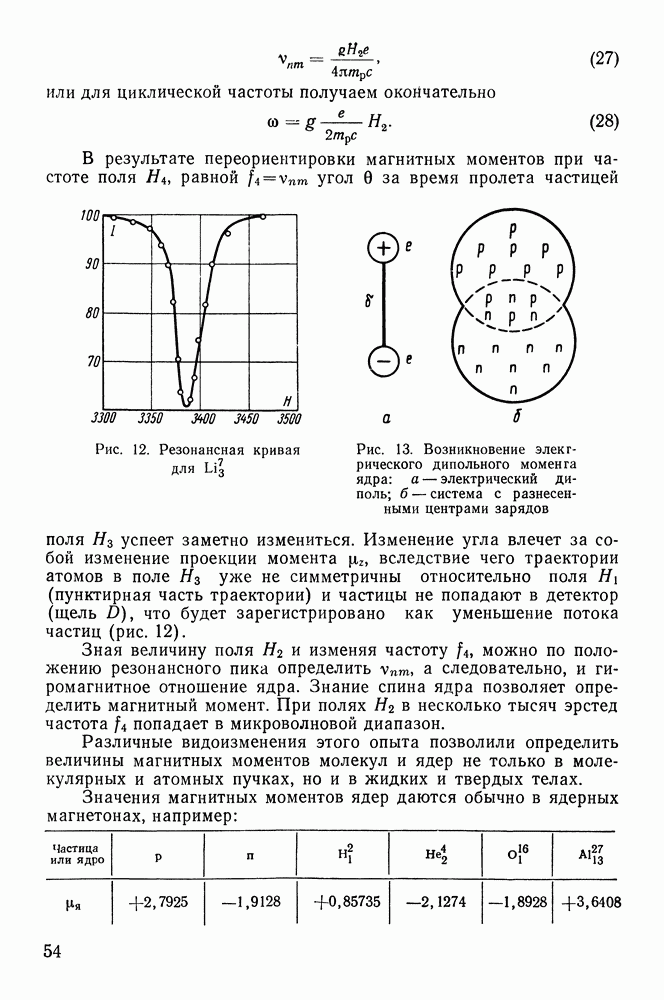
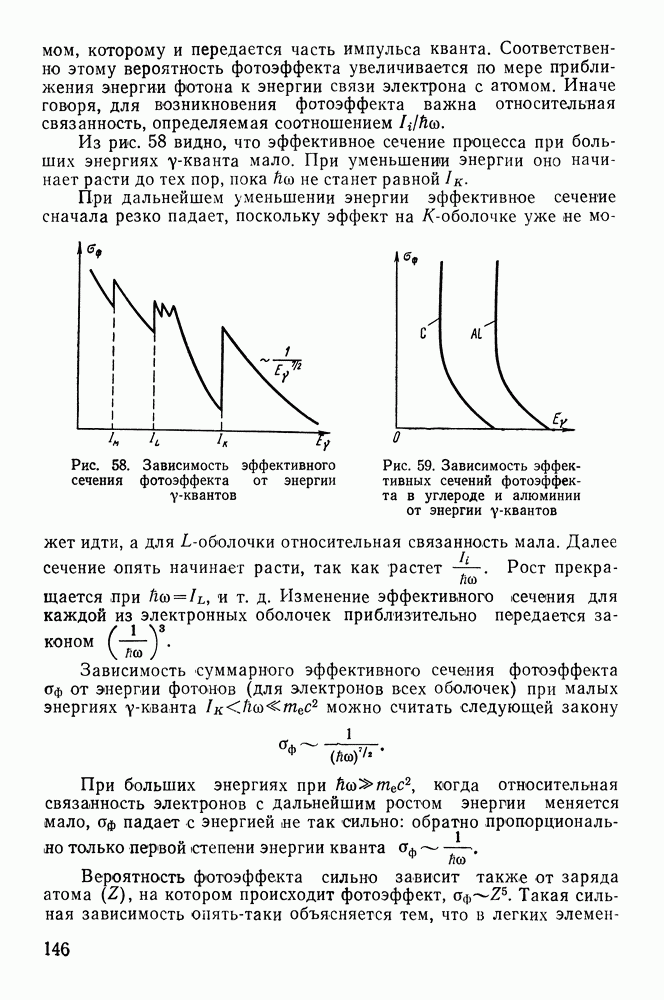
1. Первый элемент короткоживущий, второй — долгоживущий, т. е.  . В этом случае кривая, показывающая изменение суммарной активности источника, имеет вид, представленный на рис. 31, а. В начале ход кривой определяется в основном быстрым уменьшением числа активных ядер
. В этом случае кривая, показывающая изменение суммарной активности источника, имеет вид, представленный на рис. 31, а. В начале ход кривой определяется в основном быстрым уменьшением числа активных ядер  ядра В тоже распадаются, но медленно, и поэтому их распад не очень сильно влияет на наклон кривой на участке
ядра В тоже распадаются, но медленно, и поэтому их распад не очень сильно влияет на наклон кривой на участке  . В дальнейшем ядер типа А остается в смеси изотопов мало, и наклон кривой определяется постоянной распада
. В дальнейшем ядер типа А остается в смеси изотопов мало, и наклон кривой определяется постоянной распада  Если нужно найти и
Если нужно найти и  то по наклону кривой при большом значении времени находят
то по наклону кривой при большом значении времени находят  (в выражении (45) первый экспоненциальный член в этом случае может быть отброшен). Для определения величины
(в выражении (45) первый экспоненциальный член в этом случае может быть отброшен). Для определения величины  надо учесть также влияние распада долгоживущего элемента на наклон первой части кривой. Для этого экстраполируют прямую
надо учесть также влияние распада долгоживущего элемента на наклон первой части кривой. Для этого экстраполируют прямую  в область малых времен, в нескольких точках вычитают из суммарной активности активность, определяемую элементом В, по полученным значениям
в область малых времен, в нескольких точках вычитают из суммарной активности активность, определяемую элементом В, по полученным значениям
строят прямую для элемента А и по углу  находят
находят  (при этом надо переходить от логарифмов к антилогарифмам и обратно).
(при этом надо переходить от логарифмов к антилогарифмам и обратно).

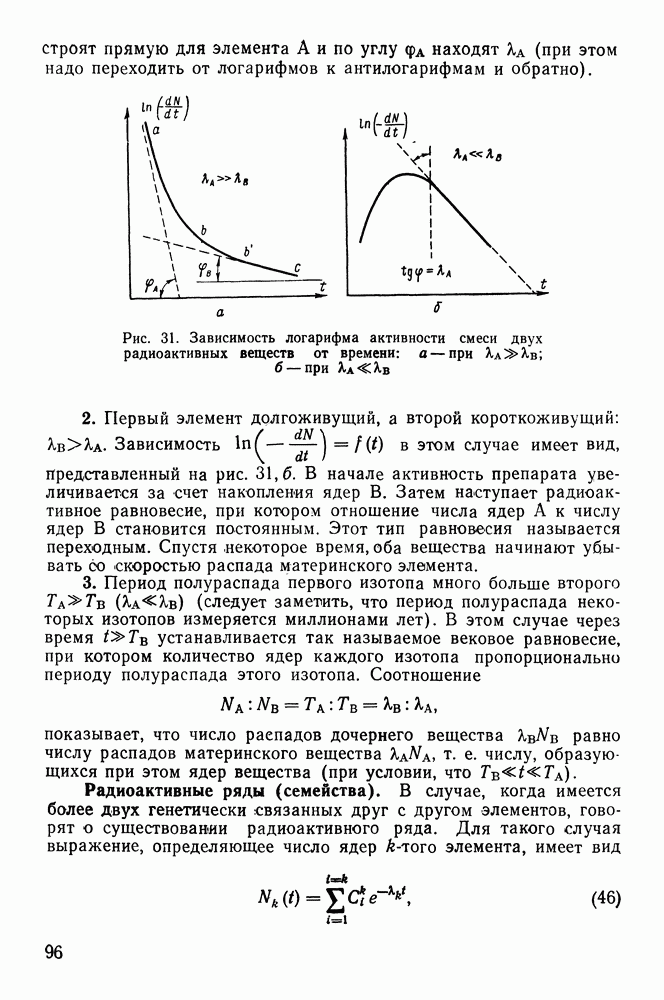
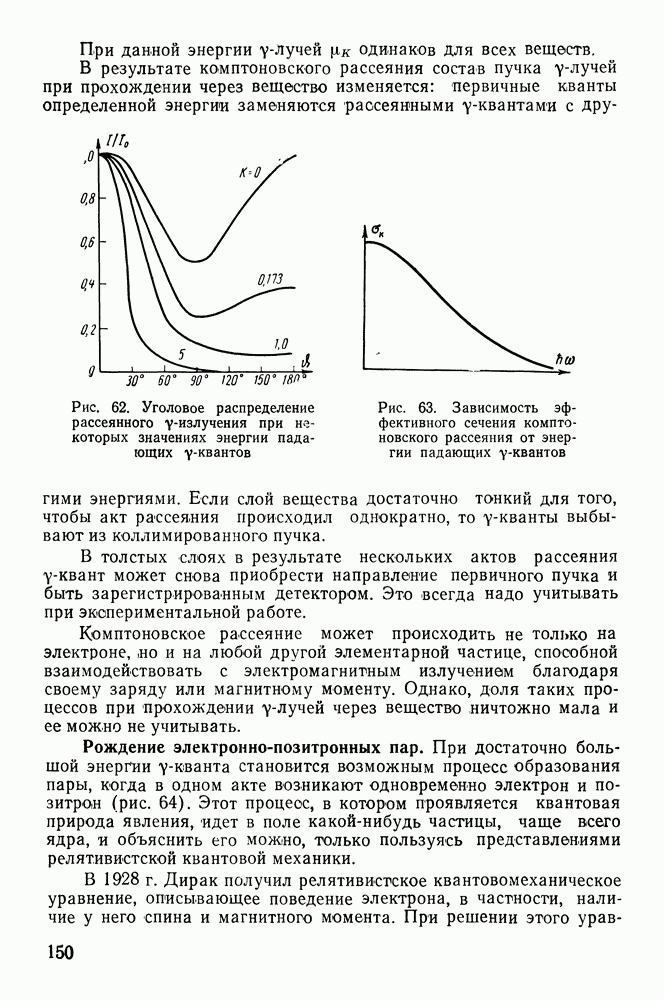
Рис. 31. Зависимость логарифма активности смеси двух радиоактивных веществ от времени: а — при  при
при 
2. Первый элемент долгоживущий, а второй короткоживущий:  Зависимость
Зависимость  в этом случае имеет вид, представленный на рис. 31,б. В начале активность препарата увеличивается за счет накопления ядер В. Затем наступает радиоактивное равновесие, при котором отношение числа ядер А к числу ядер В становится постоянным. Этот тип равновесия называется переходным. Спустя некоторое время, оба вещества начинают убывать со скоростью распада материнского элемента.
в этом случае имеет вид, представленный на рис. 31,б. В начале активность препарата увеличивается за счет накопления ядер В. Затем наступает радиоактивное равновесие, при котором отношение числа ядер А к числу ядер В становится постоянным. Этот тип равновесия называется переходным. Спустя некоторое время, оба вещества начинают убывать со скоростью распада материнского элемента.
3. Период полураспада первого изотопа много больше второго  (следует заметить, что период полураспада некоторых изотопов измеряется миллионами лет). В этом случае через время устанавливается так называемое вековое равновесие, при котором количество ядер каждого изотопа пропорционально периоду полураспада этого изотопа. Соотношение
(следует заметить, что период полураспада некоторых изотопов измеряется миллионами лет). В этом случае через время устанавливается так называемое вековое равновесие, при котором количество ядер каждого изотопа пропорционально периоду полураспада этого изотопа. Соотношение

показывает, что число раепадов дочернего вещества  равно числу распадов материнского вещества
равно числу распадов материнского вещества  т. е. числу, образующихся при этом ядер вещества (при условии, что
т. е. числу, образующихся при этом ядер вещества (при условии, что 
Радиоактивные ряды (семейства). В случае, когда имеется более двух генетически связанных друг с другом элементов, говорят о существовании радиоактивного ряда. Для такого случая выражение, определяющее число ядер А-того элемента, имеет вид

где константы  определяются характеристиками отдельных элементов.
определяются характеристиками отдельных элементов.
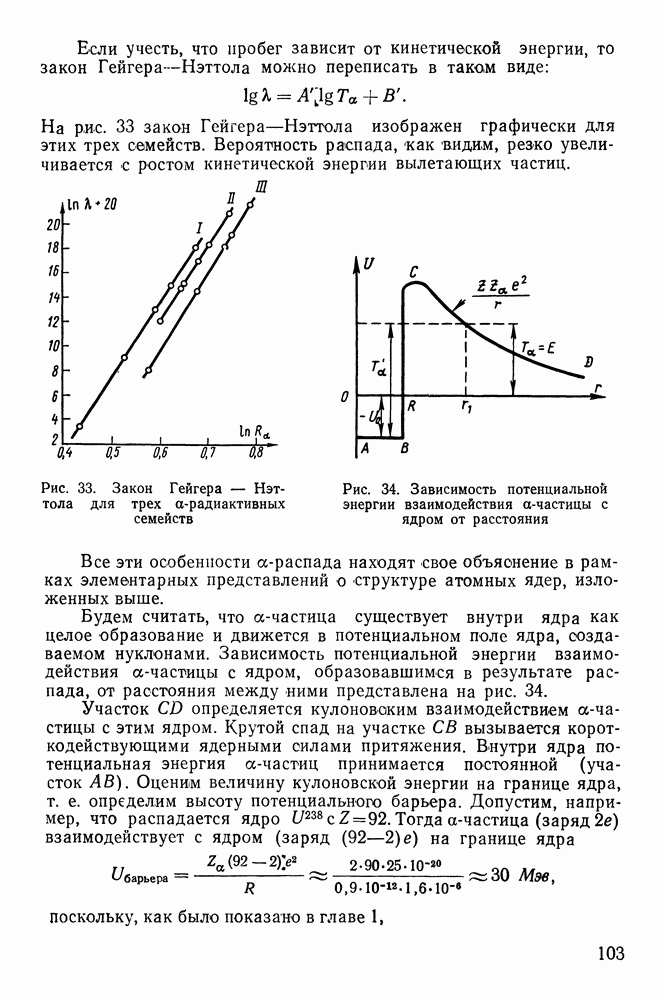
Тяжелые ядра с массовым числом  превышающим
превышающим  подвержены
подвержены  -распаду вследствие того, что в них велика роль кулоновской энергии. Если при этом массовое число намного превышает 208, то ядро переходит в стабильное путем цепи последоватальных распадов. Однако не все распады в этой цепи являются
-распаду вследствие того, что в них велика роль кулоновской энергии. Если при этом массовое число намного превышает 208, то ядро переходит в стабильное путем цепи последоватальных распадов. Однако не все распады в этой цепи являются  -распадами. При каждом
-распадами. При каждом  -распаде массовое число уменьшается на 4 единицы, а число протонов — только на два, и поэтому процент нейтронов увеличивается. В результате после потери нескольких
-распаде массовое число уменьшается на 4 единицы, а число протонов — только на два, и поэтому процент нейтронов увеличивается. В результате после потери нескольких  -частиц ядро становится склонным к
-частиц ядро становится склонным к  -распаду, при котором внутри ядра один из нейтронов превращается в протон по схеме
-распаду, при котором внутри ядра один из нейтронов превращается в протон по схеме  . В радиоактивных рядах процессы
. В радиоактивных рядах процессы  -распада и
-распада и  -распада поэтому обычно чередуются друг с другом.
-распада поэтому обычно чередуются друг с другом.
При  -распаде массовое число А изменяется на 4, а при
-распаде массовое число А изменяется на 4, а при  -распаде совсем не изменяется. Поскольку остаток от деления
-распаде совсем не изменяется. Поскольку остаток от деления  на 4 одинаков для всех ядер одного и того же ряда, для данного семейства А может быть выражено формулой:
на 4 одинаков для всех ядер одного и того же ряда, для данного семейства А может быть выражено формулой:

где С — постоянное для ряда число, а  принимает целочисленные значения.
принимает целочисленные значения.
В принципе могут существовать только четыре различных радиоактивных ряда (табл. 1), в которых А равно

Радиоактивный ряд обычно начинается с изотопа, время жизни которого очень велико и близко к времени жизни Земли  лет (имеются, правда, и исключения).
лет (имеются, правда, и исключения).
Таблица 1 (см. скан)
В третьем ряду родоначальником ряда был плутоний  лет, но он успел распасться и в естественном виде не обнаруживается.
лет, но он успел распасться и в естественном виде не обнаруживается.
Последний ряд был предсказан теоретически и создан в лабораторных условиях после усовершенствования методов искусственного получения изотопов. Естественный изотоп  за время существования Земли давно распался и
за время существования Земли давно распался и  настоящее время в земной коре тоже практически отсутствует.
настоящее время в земной коре тоже практически отсутствует.
Из сравнения периодов полураспада родоначальников становится ясно, почему в земле очень много тория и почему в естественной смеси изотопов  значительно больше, чем
значительно больше, чем  Приведем в качестве примера превращения, происходящие в ряду тория (табл. 2).
Приведем в качестве примера превращения, происходящие в ряду тория (табл. 2).
Таблица 2 (см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Масштабы физических величин.
- Особенности физических явлений в микромире.
- РАЗДЕЛ ПЕРВЫЙ. СТАБИЛЬНЫЕ ЯДРА И ЯДЕРНЫЕ СИЛЫ
- § 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ПРОТОНА И НЕЙТРОНА
- § 2. ЗАРЯД АТОМНОГО ЯДРА
- § 3. РАЗМЕРЫ АТОМНЫХ ЯДЕР
- § 4. ЭНЕРГИЯ СВЯЗИ ЯДРА
- § 5. МАССА И ЭНЕРГИЯ
- § 6. СПИН И МАГНИТНЫЙ МОМЕНТ ЯДРА
- Методы определения спинов и магнитных моментов ядер.
- § 7. КВАДРУПОЛЬНЫЙ ЭЛЕКТРИЧЕСКИЙ МОМЕНТ ЯДРА
- § 8. ЧЕТНОСТЬ ВОЛНОВОЙ ФУНКЦИИ
- § 9. ЯДЕРНЫЕ МОДЕЛИ
- Глава вторая. ЯДЕРНЫЕ СИЛЫ
- § 10. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДЕРНЫХ СИЛ
- § 11. ФИЗИЧЕСКИЕ ОБОСНОВАНИЯ МЕЗОННОИ ТЕОРИИ ЯДЕРНЫХ СИЛ
- § 12. СТРУКТУРА НУКЛОНА
- § 13. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДЕЙТОНА
- Магнитный момент дейтона.
- РАЗДЕЛ ВТОРОЙ. НЕУСТОЙЧИВЫЕ ЯДРА
- § 14. ОТКРЫТИЕ РАДИОАКТИВНОСТИ
- § 15. ЗАКОНЫ РАДИОАКТИВНОГО РАСПАДА
- § 16. ТРАНСУРАНОВЫЕ ЭЛЕМЕНТЫ
- § 17. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ ИЗОТОПОВ
- § 18. АЛЬФА-РАСПАД
- § 19. БЕТА-РАСПАД
- Энергетические спектры электронов при b-распаде и роль нейтрино.
- Энергетические соотношения при b-распаде.
- § 20. ГАММА-ИЗЛУЧЕНИЕ ЯДЕР
- Ядерная изомерия.
- Эффект Мёссбауера.
- ГЛАВА ЧЕТВЕРТАЯ. ВЗАИМОДЕЙСТВИЕ ЯДЕРНОГО ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
- § 21. ВИДЫ ВЗАИМОДЕЙСТВИЯ
- § 22. ВЗАИМОДЕЙСТВИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ СО СРЕДОЙ
- Пробег заряженных частиц в веществе.
- § 23. КУЛОНОВСКОЕ ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ С ЯДРАМИ (УПРУГОЕ РАССЕЯНИЕ)
- § 24. ЯДЕРНОЕ ВЗАИМОДЕЙСТВИЕ
- § 25. ИЗЛУЧЕНИЕ ВАВИЛОВА — ЧЕРЕНКОВА
- § 26. ПРОХОЖДЕНИЕ ГАММА-ИЗЛУЧЕНИЯ ЧЕРЕЗ ВЕЩЕСТВО
- Рассеяние y-лучей. Эффект Комптона.
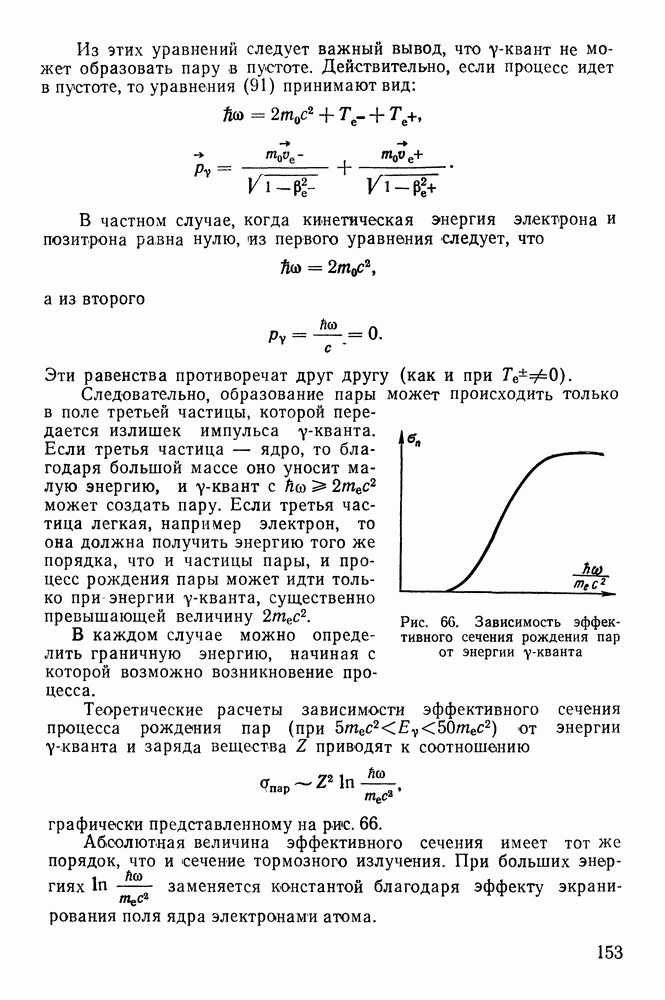
- Рождение электронно-позитронных пар.
- Другие эффекты, возникающие при поглощении y-лучей
- Суммарный коэффициент поглощения y-излучения
- Процесс аннигиляции электронно-позитронных пар.
- § 27. МЕТОДЫ РЕГИСТРАЦИИ ИЗЛУЧЕНИЯ
- РАЗДЕЛ ТРЕТИЙ. ЯДЕРНЫЕ РЕАКЦИИ
- ГЛАВА ПЯТАЯ. ЗАКОНОМЕРНОСТИ ЯДЕРНЫХ РЕАКЦИЙ
- § 29. ЗАКОНЫ СОХРАНЕНИЯ В ЯДЕРНЫХ РЕАКЦИЯХ
- § 30. РАЗЛИЧНЫЕ МЕХАНИЗМЫ РЕАКЦИЙ
- ГЛАВА ШЕСТАЯ. ФИЗИКА НЕЙТРОНОВ
- § 31. ОТКРЫТИЕ НЕЙТРОНА И ЕГО СВОЙСТВА
- § 32. ИСТОЧНИКИ НЕЙТРОНОВ
- § 33. ВЗАИМОДЕЙСТВИЕ НЕЙТРОНОВ С ВЕЩЕСТВОМ
- § 34. МЕТОДЫ РЕГИСТРАЦИИ НЕЙТРОНОВ
- § 35. ЗАМЕДЛЕНИЕ НЕЙТРОНОВ
- § 36. МЕТОДЫ ПОЛУЧЕНИЯ МОНОХРОМАТИЧЕСКИХ НЕЙТРОНОВ
- ГЛАВА СЕДЬМАЯ. ДЕЛЕНИЕ И СИНТЕЗ ЯДЕР
- § 37. ОТКРЫТИЕ ДЕЛЕНИЯ ЯДЕР
- § 38. ПРОЦЕССЫ, ПРОИСХОДЯЩИЕ ПРИ ДЕЛЕНИИ ЯДЕР УРАНА
- § 39. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДЕЛЕНИЯ
- § 40. ТИПЫ РЕАКЦИЙ ДЕЛЕНИЯ
- § 41. ВОЗМОЖНОСТЬ ИСПОЛЬЗОВАНИЯ ЯДЕРНОЙ ЭНЕРГИИ
- § 42. ЦЕПНАЯ ЯДЕРНАЯ РЕАКЦИЯ И ЯДЕРНЫЕ РЕАКТОРЫ
- § 43. ТЕРМОЯДЕРНЫЙ СИНТЕЗ
- Термоядерные реакции в лабораторных условиях.
- РАЗДЕЛ ЧЕТВЕРТЫЙ. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И КОСМИЧЕСКИЕ ЛУЧИ
- § 44. ОТКРЫТИЕ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
- § 45. ВИДЫ ВЗАИМОДЕЙСТВИЯ ЧАСТИЦ
- § 46. КЛАССИФИКАЦИЯ ЧАСТИЦ
- § 47. РЕАКЦИИ МЕЖДУ ЧАСТИЦАМИ
- § 48. ВНУТРЕННИЕ СВОЙСТВА ЧАСТИЦ
- § 49. РЕЗОНАНСЫ
- § 50. ПОПЫТКИ СИСТЕМАТИЗАЦИИ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
- § 51. ГИПЕРФРАГМЕНТЫ (ИЛИ Л°-ЯДРА)
- § 52. НАРУШЕНИЕ ЗАКОНА СОХРАНЕНИЯ ЧЕТНОСТИ
- § 53. ФИЗИКА НЕЙТРИНО
- ГЛАВА ДЕВЯТАЯ. КОСМИЧЕСКИЕ ЛУЧИ
- § 54. ОТКРЫТИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- § 55. ПЕРВИЧНОЕ ИЗЛУЧЕНИЕ У ЗЕМЛИ
- § 56. ВЗАИМОДЕЙСТВИЕ КОСМИЧЕСКОГО ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
- § 57. СОСТАВ КОСМИЧЕСКИХ ЛУЧЕЙ НА УРОВНЕ МОРЯ
- § 58. ВРЕМЕННЫЕ ИЗМЕНЕНИЯ ИНТЕНСИВНОСТИ КОСМИЧЕСКИХ ЛУЧЕЙ
- § 59. РАДИАЦИОННЫЕ ПОЯСА
- § 60. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА