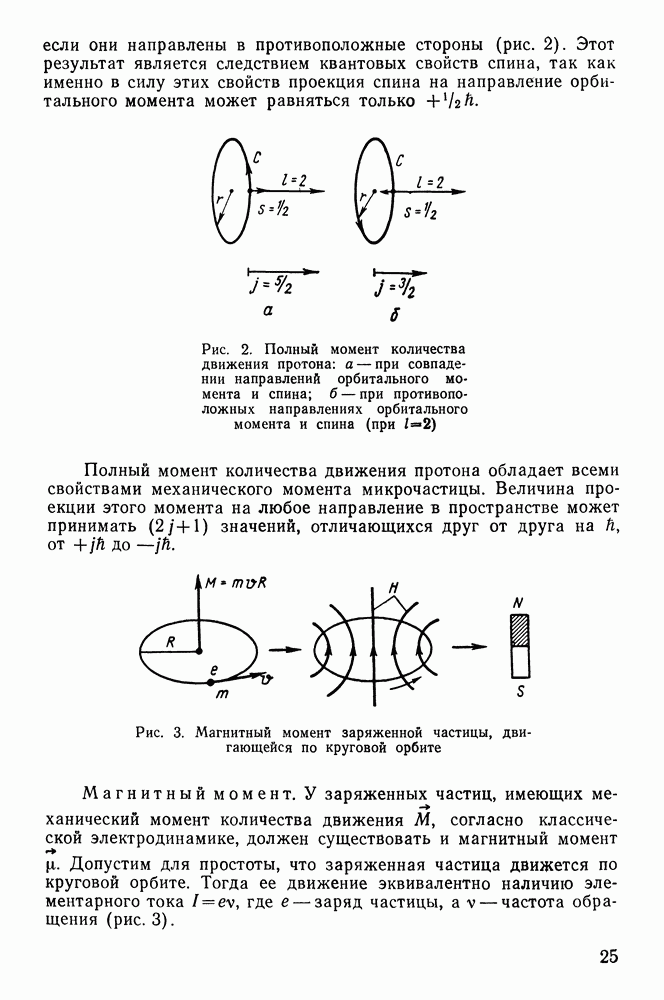
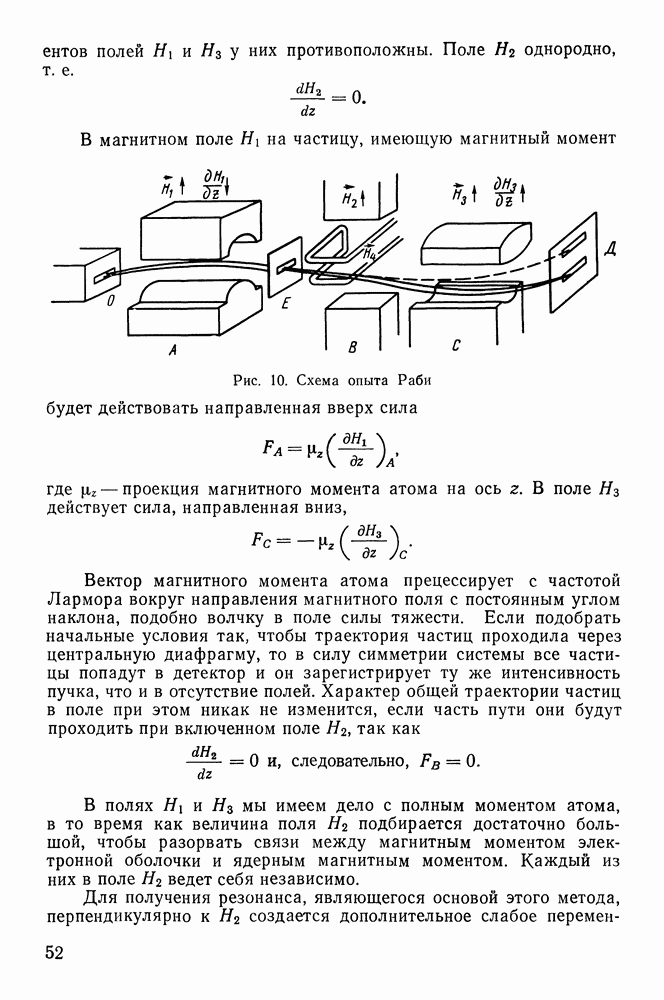
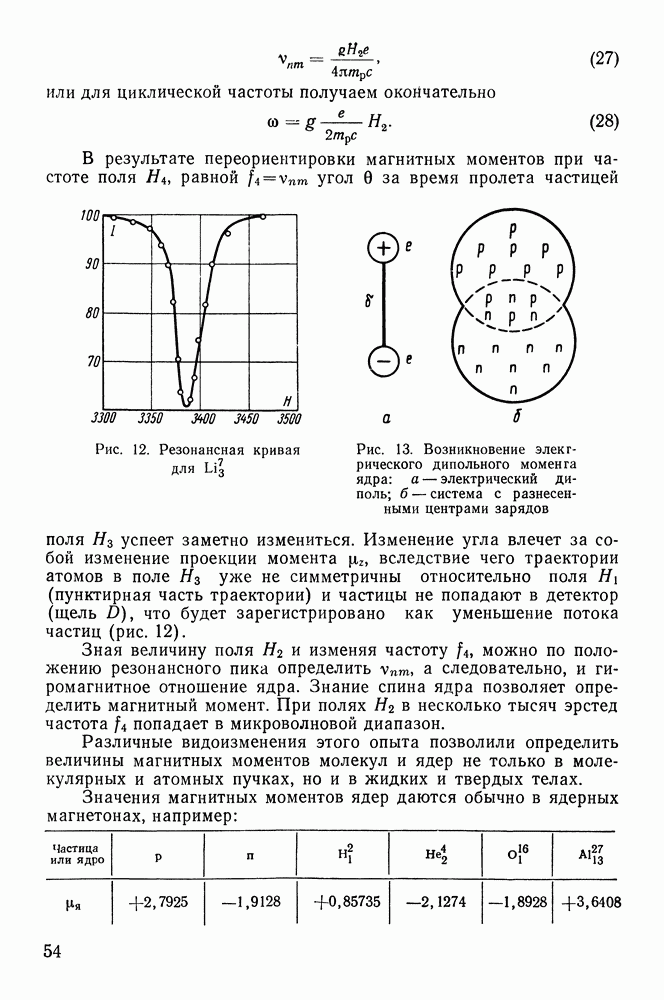
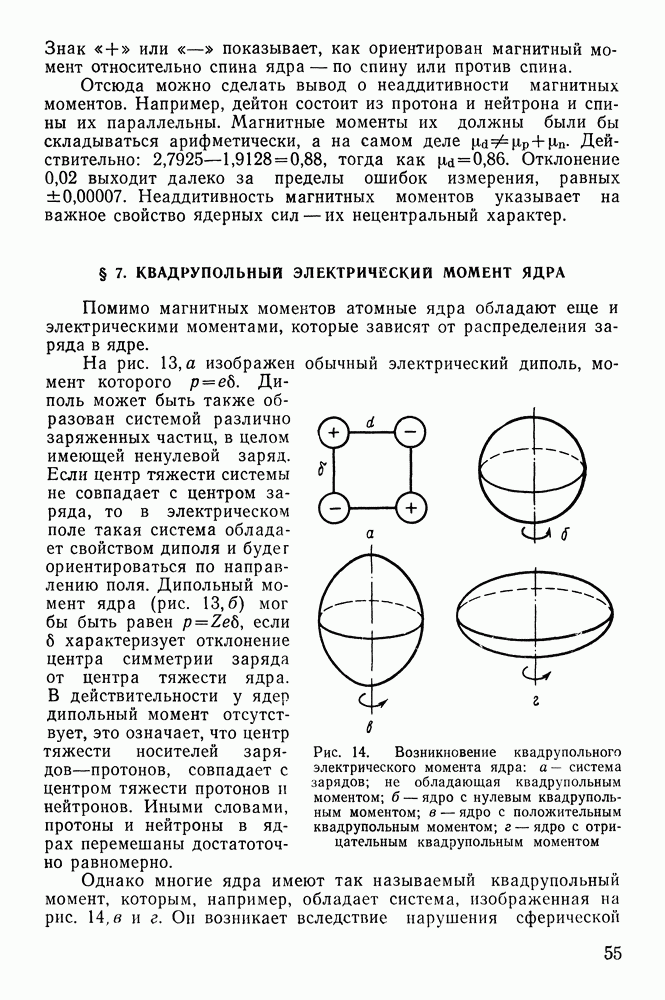
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. СПИН И МАГНИТНЫЙ МОМЕНТ ЯДРА
Спин ядра. Полный момент количества движения ядра слагается из моментов количества движения, входящих в него протонов и нейтронов. Последние, в свою очередь, обладают собственными моментами количества движения и орбитальными моментами, обусловленными движением относительно общего центра инерции ядра.
Выше уже говорилось, что абсолютная величина собственного момента количества движения нуклона выражается через спиновое квантовое число  с помощью соотношения
с помощью соотношения

Если система состоит из двух частиц, спины которых равны  и 52, то собственный момент системы
и 52, то собственный момент системы

где суммарное спиновое число  может иметь значения [4]
может иметь значения [4]

так что

или векторно

Если в системе имеется большее число частиц, между которыми действуют только центральные силы, то суммарный спиновый момент находится сложением всех векторов:

Орбитальный момент частицы выражается через орбитальное квантовое число I:

Сложение орбитальных квантовых моментов в этом случае выполняется совершенно так же, как и спиновых

Сумма орбитального и спинового моментов, образованная таким же образом, дает полный момент количества движения ядра 1

Абсолютная величина полного момента количества движения ядра находится из соотношения

где квантовое число I может принимать значения 
Если бы полные моменты всех нуклонов были направлены в одну сторону, то суммарная величина механического момента ядра с числом нуклонов  заведомо превышала бы
заведомо превышала бы  Однако ни одно из известных ядер не имеет и десятой доли такого значения. Это говорит о том, что у большинства пар нуклонов полные механические моменты ориентированы в противоположных направлениях.
Однако ни одно из известных ядер не имеет и десятой доли такого значения. Это говорит о том, что у большинства пар нуклонов полные механические моменты ориентированы в противоположных направлениях.
Так как полный момент отдельного нуклона является полуцелым (в единицах  то в зависимости от четности числа нуклонов в ядре момент I будет либо целым, либо полуцелым.
то в зависимости от четности числа нуклонов в ядре момент I будет либо целым, либо полуцелым.
Ядра с четным числом частиц А имеют целый механический момент, а ядра с нечетным значением А имеют полуцелый механический момент в единицах 
Например, если составить ядро из двух нуклонов с полными моментами  то момент количества движения ядра может равняться одному из целочисленных значений величины стороны треугольника, две другие стороны которого равны
то момент количества движения ядра может равняться одному из целочисленных значений величины стороны треугольника, две другие стороны которого равны  и 3/2:
и 3/2:

Поскольку сторона треугольника не может быть больше суммы или меньше разности двух других сторон, то механический момент ядра в рассматриваемом случае может принимать только одно из следующих значений: 
Проекция момента количества движения ядра на одну из координатных осей (обычно рассматривают проекцию на ось  характеризуется с помощью магнитного квантового числа
характеризуется с помощью магнитного квантового числа 

причем  может принимать
может принимать  значений
значений

Проекции I на остальные две оси не могут быть точно определены одновременно с 
Полный момент количества движения ядра I всегда является интегралом движения. Орбитальный  и спиновый
и спиновый  моменты количества движения ядра каждый в отдельности не являются интегралами движения, поскольку ядерные силы нецентральны и существует спин-орбитальное взаимодействие (подробнее см. в § 9).
моменты количества движения ядра каждый в отдельности не являются интегралами движения, поскольку ядерные силы нецентральны и существует спин-орбитальное взаимодействие (подробнее см. в § 9).
Полный момент количества движения ядра называют спином ядра: поскольку, как и для отдельного нуклона, это внутренний момент количества движения системы — ядра, рассматриваемого в целом как одна частица.
Из измерений величины спинов ядер можно прийти к заключению, что электроны не могут входить в состав ядра. Рассмотрим для этого, например, ядро азота  До открытия нейтронов считалось, что ядро состоит из протонов и электронов. При этом в ядре азота должно было содержаться
До открытия нейтронов считалось, что ядро состоит из протонов и электронов. При этом в ядре азота должно было содержаться  т. е. 21 частица. Спины и протона и электрона равны
т. е. 21 частица. Спины и протона и электрона равны  Следовательно, спин ядра азота должен был быть полуцелым, тогда как экспериментально измеренное значение спина ядра азота оказалось равным 1. В свое время этот факт получил название «азотная катастрофа».
Следовательно, спин ядра азота должен был быть полуцелым, тогда как экспериментально измеренное значение спина ядра азота оказалось равным 1. В свое время этот факт получил название «азотная катастрофа».
На самом деле ядро азота состоит из  т. е. всего из 14 частиц, и спин его должен быть целым.
т. е. всего из 14 частиц, и спин его должен быть целым.
Магнитные моменты ядер. Магнитный момент ядра, состоящего из А нуклонов, обусловлен спиновыми магнитными моментами нуклонов и магнитными моментами, вызванными орбитальным движением протонов. Однако вектор магнитного момента не совпадает с вектором момента количества движения (рис. 8). Благодаря магнитному взаимодействию, существующему между орбитальным и спиновыми моментами, результирующий магнитный момент  прецессирует относительно результирующего момента количества движения
прецессирует относительно результирующего момента количества движения  При этом среднее по времени и, обозначаемое
При этом среднее по времени и, обозначаемое  есть составляющая магнитного момента направленная вдоль момента количества движения ядра.
есть составляющая магнитного момента направленная вдоль момента количества движения ядра.
Когда вдоль оси  приложено внешнее магнитное поле, проекция
приложено внешнее магнитное поле, проекция  на ось принимает
на ось принимает  значений, величина которых зависит от угла, образованного вектором и осью. Максимальное значение этой проекции мы и будем в дальнейшем обозначать и называть магнитным моментом ядра.
значений, величина которых зависит от угла, образованного вектором и осью. Максимальное значение этой проекции мы и будем в дальнейшем обозначать и называть магнитным моментом ядра.
В связи с тем что «эффективный» магнитный момент ведет

Рис. 8. Образование магнитного момента ядра
себя как вектор, направленный вдоль момента количества движения, оба момента — механический и магнитный — связаны линейной зависимостью:

где  гиромагнитное отношение для ядра.
гиромагнитное отношение для ядра.
Как уже говорилось, если  выражать в единицах ядерного магнетона, а I в единицах
выражать в единицах ядерного магнетона, а I в единицах  то для
то для  ядра получим:
ядра получим:

Теоретически нельзя определить значение  так как для этого надо знать, каким образом полный момент ядра
так как для этого надо знать, каким образом полный момент ядра  составляется из орбитальных и спиновых моментов нуклонов ядра. Поэтому
составляется из орбитальных и спиновых моментов нуклонов ядра. Поэтому  или I определяют экспериментально.
или I определяют экспериментально.
Из опыта известно, что магнитные моменты ядер либо равны нулю, либо имеют значение порядка ядерного магнетона. Это тоже является одним из аргументов в пользу того, что в составе ядра не может быть электронов, так как магнитный момент электрона примерно в 2000 раз больше, чем 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Масштабы физических величин.
- Особенности физических явлений в микромире.
- РАЗДЕЛ ПЕРВЫЙ. СТАБИЛЬНЫЕ ЯДРА И ЯДЕРНЫЕ СИЛЫ
- § 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ПРОТОНА И НЕЙТРОНА
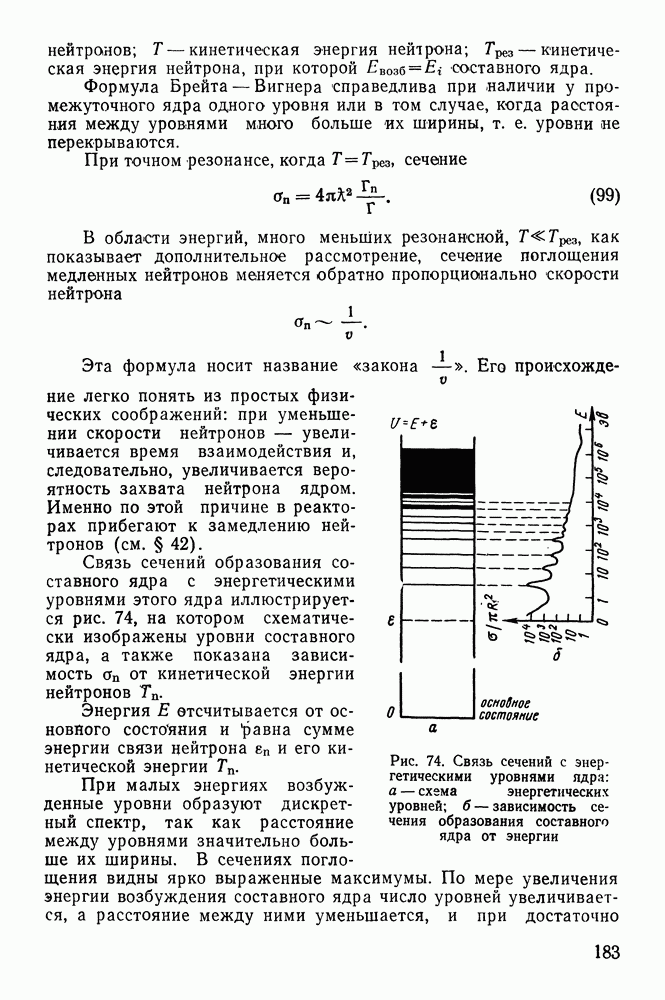
- § 2. ЗАРЯД АТОМНОГО ЯДРА
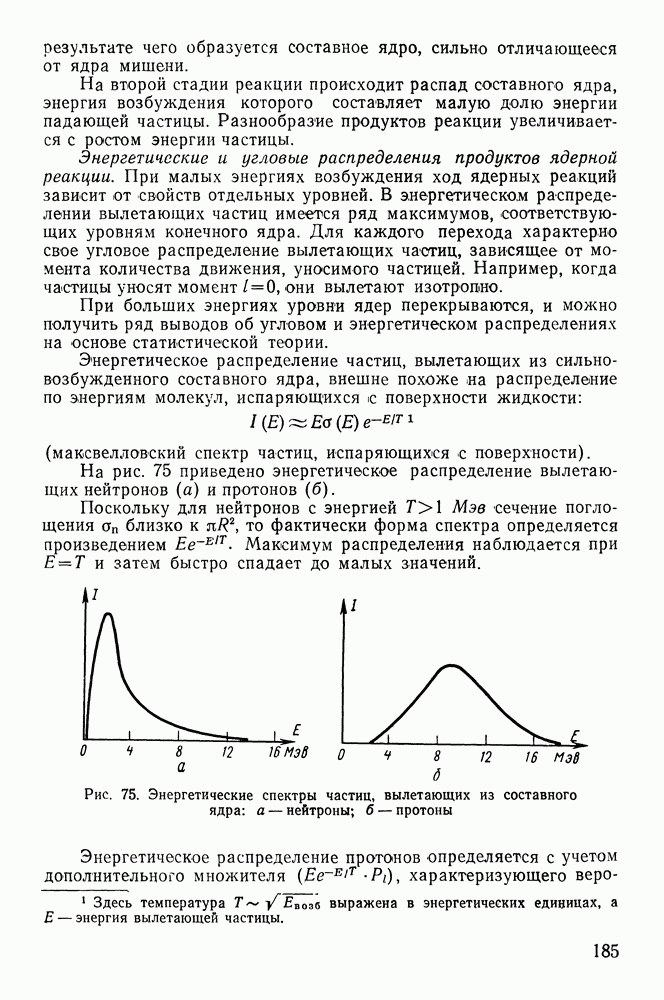
- § 3. РАЗМЕРЫ АТОМНЫХ ЯДЕР
- § 4. ЭНЕРГИЯ СВЯЗИ ЯДРА
- § 5. МАССА И ЭНЕРГИЯ
- § 6. СПИН И МАГНИТНЫЙ МОМЕНТ ЯДРА
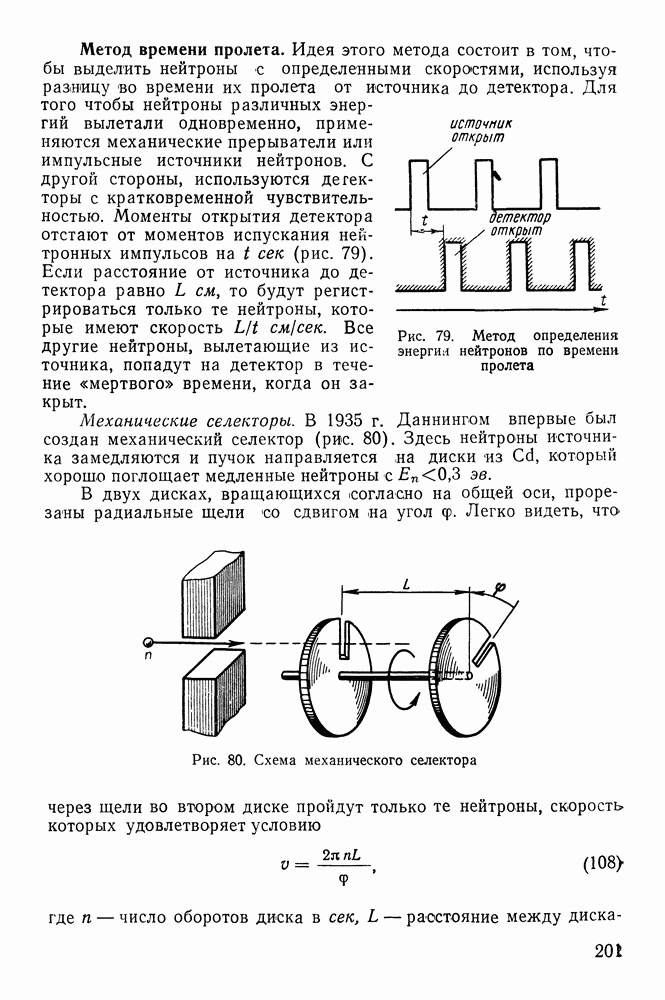
- Методы определения спинов и магнитных моментов ядер.
- § 7. КВАДРУПОЛЬНЫЙ ЭЛЕКТРИЧЕСКИЙ МОМЕНТ ЯДРА
- § 8. ЧЕТНОСТЬ ВОЛНОВОЙ ФУНКЦИИ
- § 9. ЯДЕРНЫЕ МОДЕЛИ
- Глава вторая. ЯДЕРНЫЕ СИЛЫ
- § 10. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДЕРНЫХ СИЛ
- § 11. ФИЗИЧЕСКИЕ ОБОСНОВАНИЯ МЕЗОННОИ ТЕОРИИ ЯДЕРНЫХ СИЛ
- § 12. СТРУКТУРА НУКЛОНА
- § 13. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДЕЙТОНА
- Магнитный момент дейтона.
- РАЗДЕЛ ВТОРОЙ. НЕУСТОЙЧИВЫЕ ЯДРА
- § 14. ОТКРЫТИЕ РАДИОАКТИВНОСТИ
- § 15. ЗАКОНЫ РАДИОАКТИВНОГО РАСПАДА
- § 16. ТРАНСУРАНОВЫЕ ЭЛЕМЕНТЫ
- § 17. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ ИЗОТОПОВ
- § 18. АЛЬФА-РАСПАД
- § 19. БЕТА-РАСПАД
- Энергетические спектры электронов при b-распаде и роль нейтрино.
- Энергетические соотношения при b-распаде.
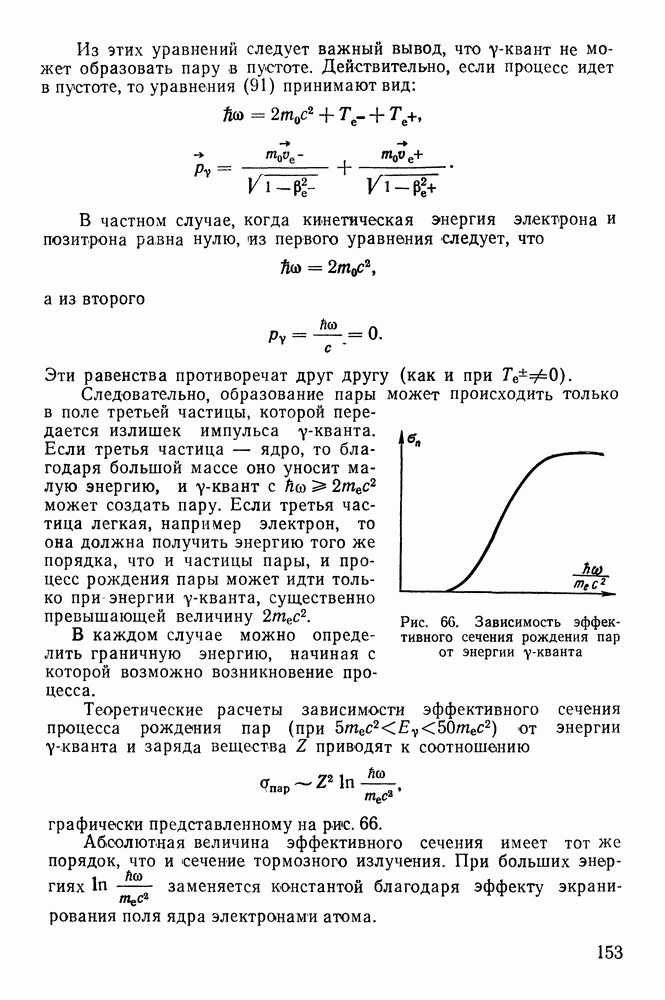
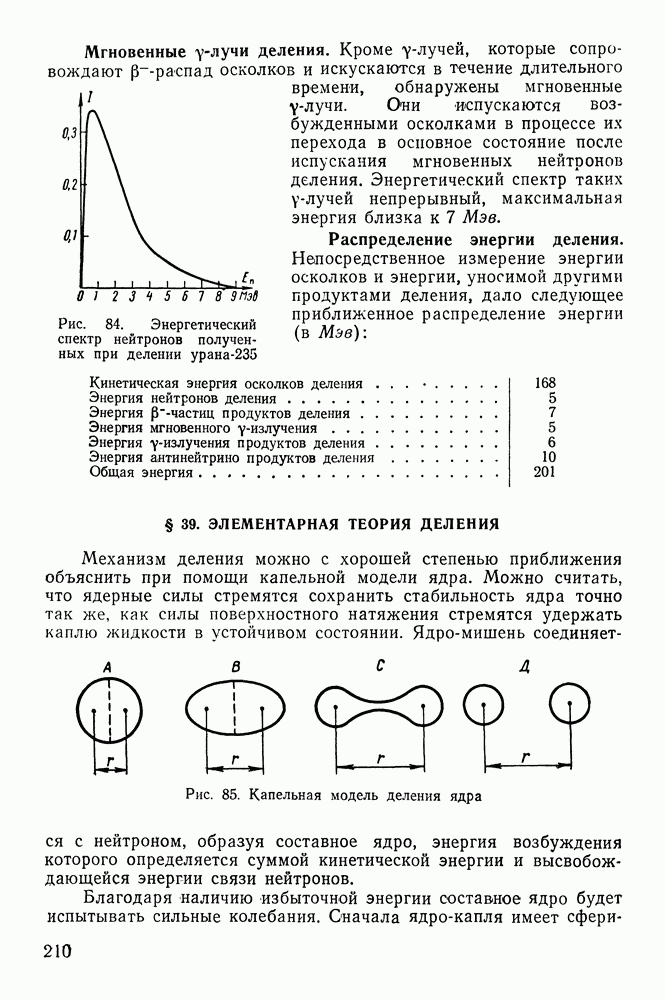
- § 20. ГАММА-ИЗЛУЧЕНИЕ ЯДЕР
- Ядерная изомерия.
- Эффект Мёссбауера.
- ГЛАВА ЧЕТВЕРТАЯ. ВЗАИМОДЕЙСТВИЕ ЯДЕРНОГО ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
- § 21. ВИДЫ ВЗАИМОДЕЙСТВИЯ
- § 22. ВЗАИМОДЕЙСТВИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ СО СРЕДОЙ
- Пробег заряженных частиц в веществе.
- § 23. КУЛОНОВСКОЕ ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ С ЯДРАМИ (УПРУГОЕ РАССЕЯНИЕ)
- § 24. ЯДЕРНОЕ ВЗАИМОДЕЙСТВИЕ
- § 25. ИЗЛУЧЕНИЕ ВАВИЛОВА — ЧЕРЕНКОВА
- § 26. ПРОХОЖДЕНИЕ ГАММА-ИЗЛУЧЕНИЯ ЧЕРЕЗ ВЕЩЕСТВО
- Рассеяние y-лучей. Эффект Комптона.
- Рождение электронно-позитронных пар.
- Другие эффекты, возникающие при поглощении y-лучей
- Суммарный коэффициент поглощения y-излучения
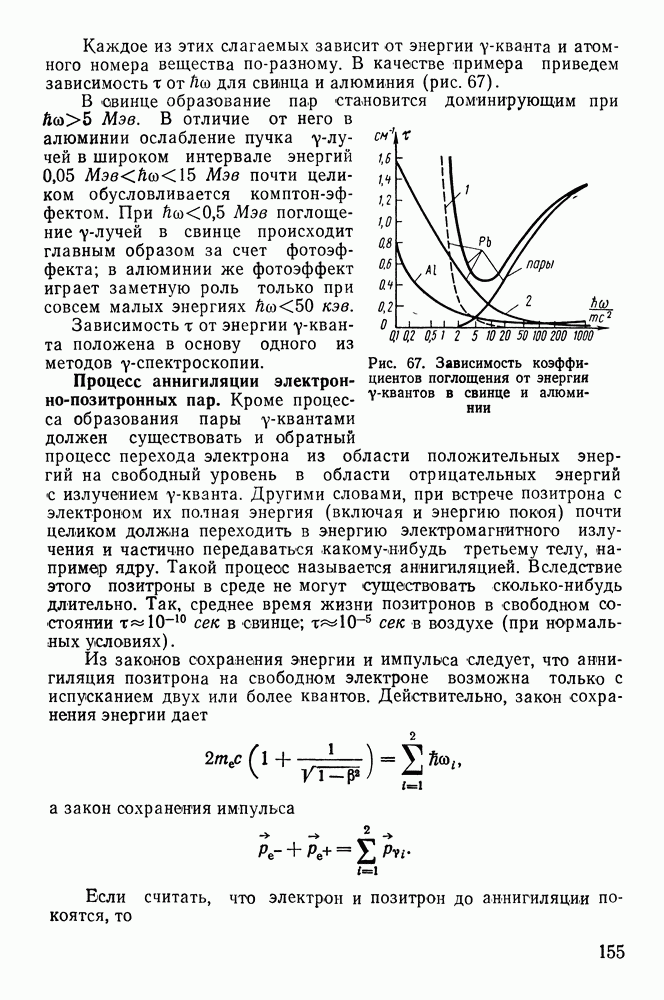
- Процесс аннигиляции электронно-позитронных пар.
- § 27. МЕТОДЫ РЕГИСТРАЦИИ ИЗЛУЧЕНИЯ
- РАЗДЕЛ ТРЕТИЙ. ЯДЕРНЫЕ РЕАКЦИИ
- ГЛАВА ПЯТАЯ. ЗАКОНОМЕРНОСТИ ЯДЕРНЫХ РЕАКЦИЙ
- § 29. ЗАКОНЫ СОХРАНЕНИЯ В ЯДЕРНЫХ РЕАКЦИЯХ
- § 30. РАЗЛИЧНЫЕ МЕХАНИЗМЫ РЕАКЦИЙ
- ГЛАВА ШЕСТАЯ. ФИЗИКА НЕЙТРОНОВ
- § 31. ОТКРЫТИЕ НЕЙТРОНА И ЕГО СВОЙСТВА
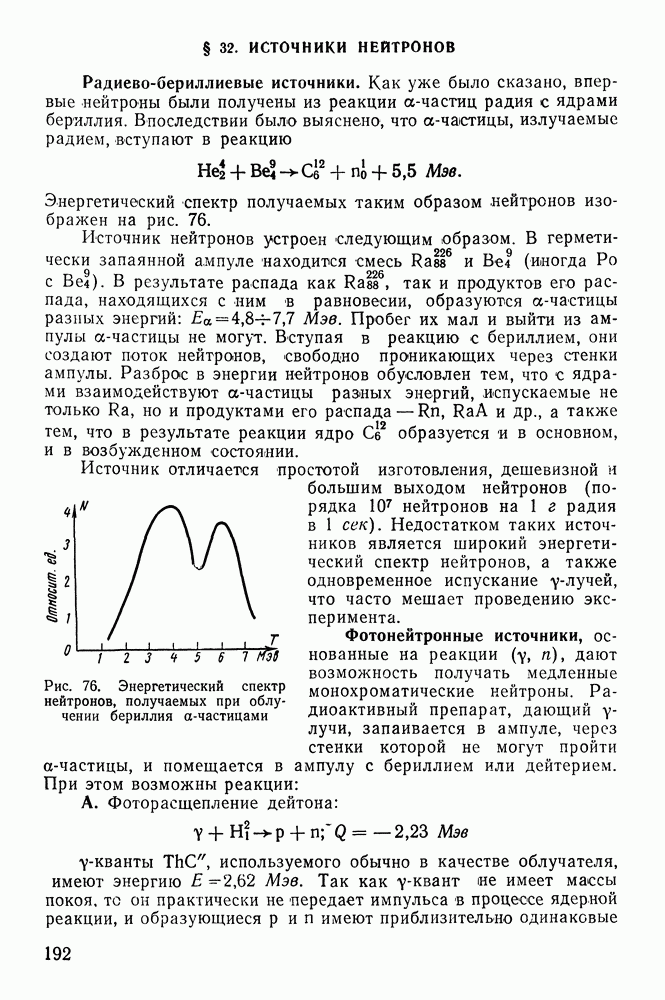
- § 32. ИСТОЧНИКИ НЕЙТРОНОВ
- § 33. ВЗАИМОДЕЙСТВИЕ НЕЙТРОНОВ С ВЕЩЕСТВОМ
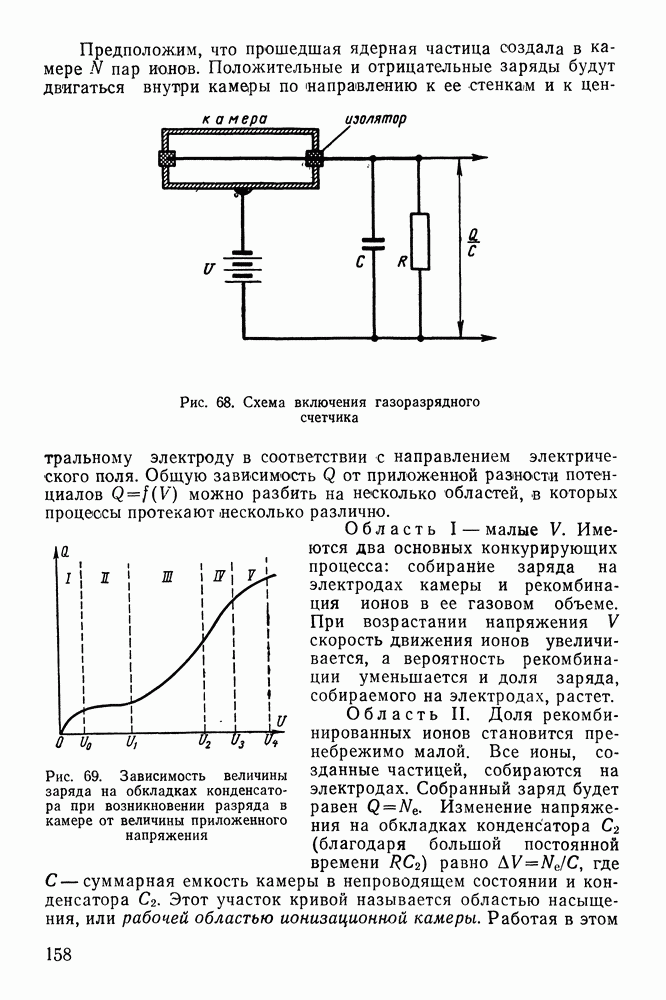
- § 34. МЕТОДЫ РЕГИСТРАЦИИ НЕЙТРОНОВ
- § 35. ЗАМЕДЛЕНИЕ НЕЙТРОНОВ
- § 36. МЕТОДЫ ПОЛУЧЕНИЯ МОНОХРОМАТИЧЕСКИХ НЕЙТРОНОВ
- ГЛАВА СЕДЬМАЯ. ДЕЛЕНИЕ И СИНТЕЗ ЯДЕР
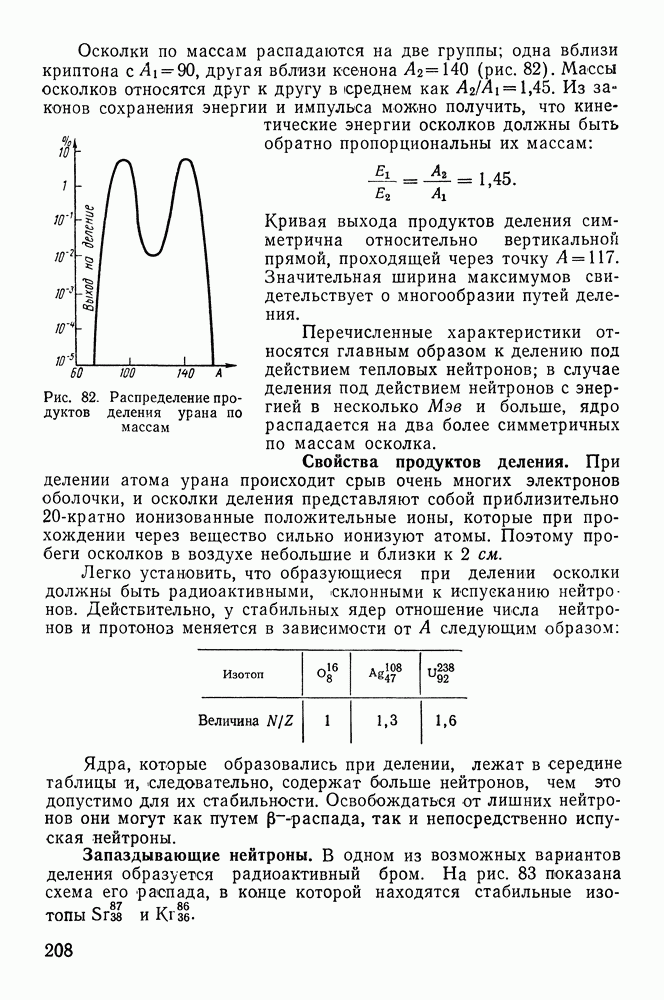
- § 37. ОТКРЫТИЕ ДЕЛЕНИЯ ЯДЕР
- § 38. ПРОЦЕССЫ, ПРОИСХОДЯЩИЕ ПРИ ДЕЛЕНИИ ЯДЕР УРАНА
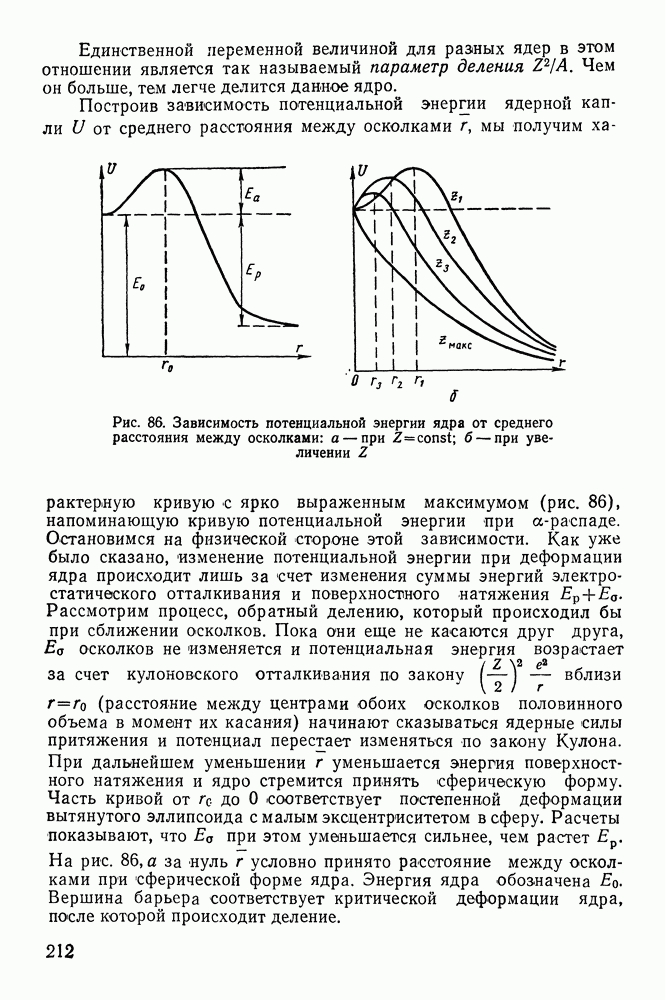
- § 39. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДЕЛЕНИЯ
- § 40. ТИПЫ РЕАКЦИЙ ДЕЛЕНИЯ
- § 41. ВОЗМОЖНОСТЬ ИСПОЛЬЗОВАНИЯ ЯДЕРНОЙ ЭНЕРГИИ
- § 42. ЦЕПНАЯ ЯДЕРНАЯ РЕАКЦИЯ И ЯДЕРНЫЕ РЕАКТОРЫ
- § 43. ТЕРМОЯДЕРНЫЙ СИНТЕЗ
- Термоядерные реакции в лабораторных условиях.
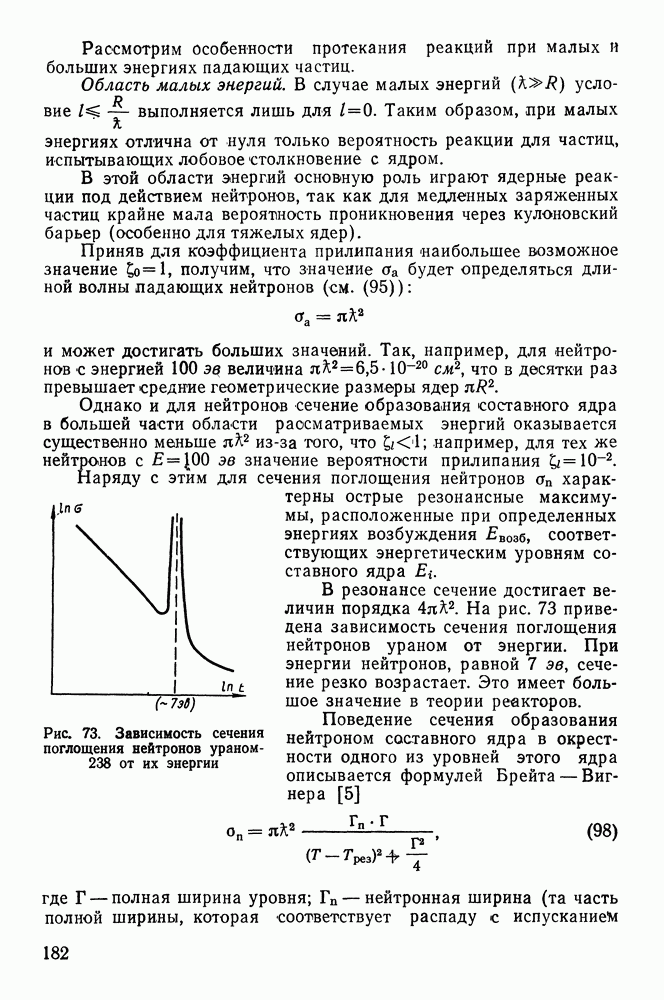
- РАЗДЕЛ ЧЕТВЕРТЫЙ. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И КОСМИЧЕСКИЕ ЛУЧИ
- § 44. ОТКРЫТИЕ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
- § 45. ВИДЫ ВЗАИМОДЕЙСТВИЯ ЧАСТИЦ
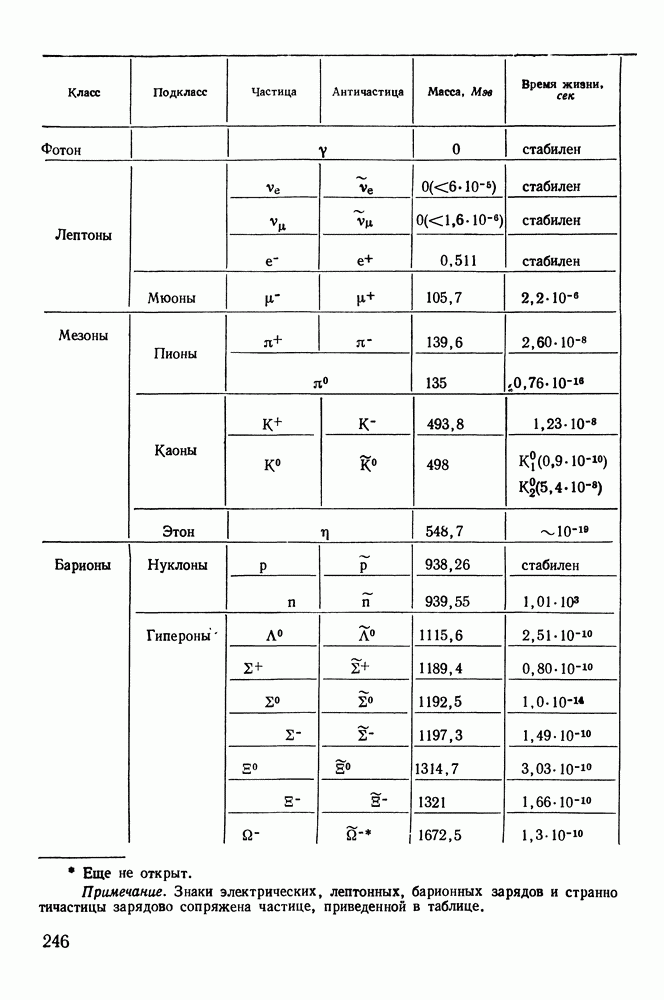
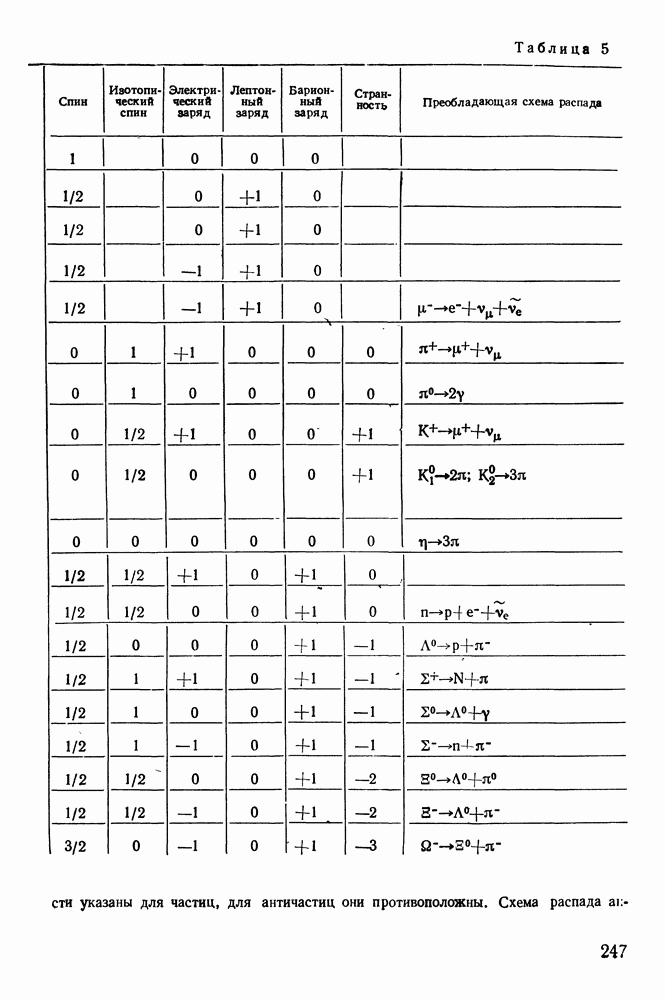
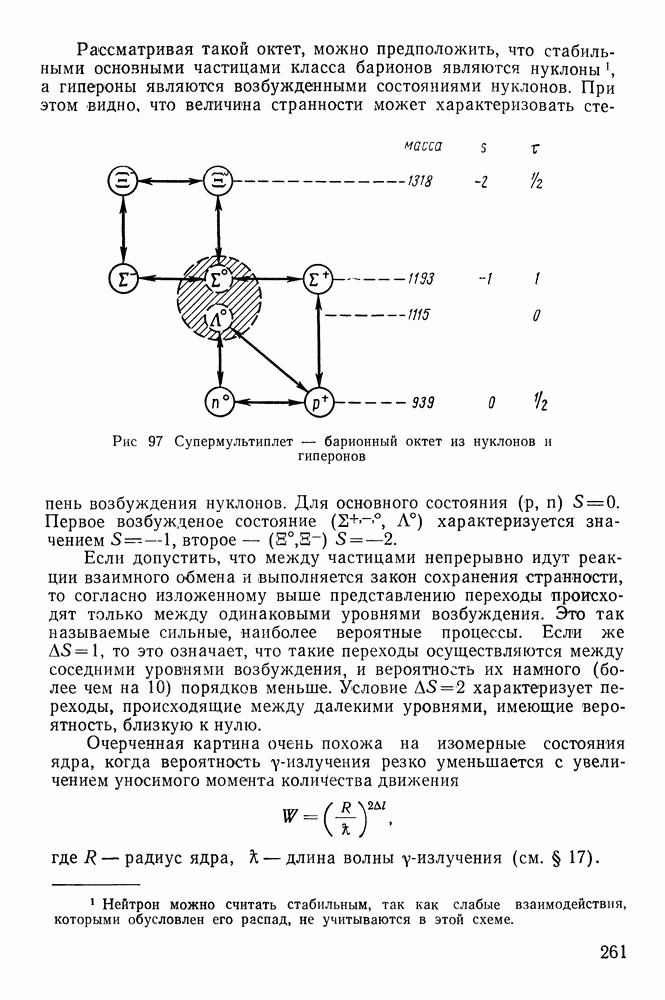
- § 46. КЛАССИФИКАЦИЯ ЧАСТИЦ
- § 47. РЕАКЦИИ МЕЖДУ ЧАСТИЦАМИ
- § 48. ВНУТРЕННИЕ СВОЙСТВА ЧАСТИЦ
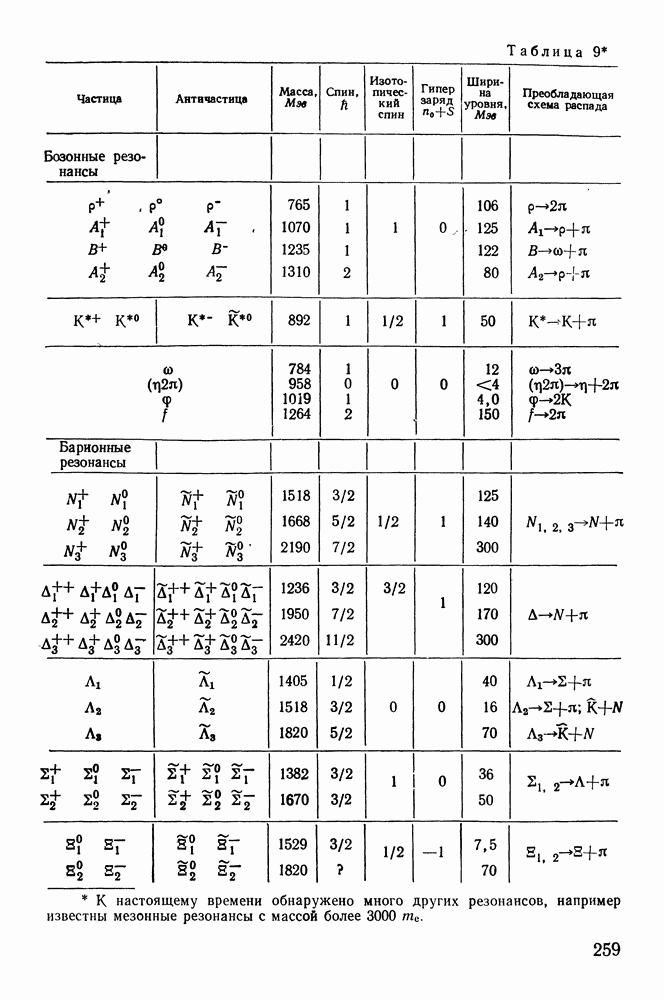
- § 49. РЕЗОНАНСЫ
- § 50. ПОПЫТКИ СИСТЕМАТИЗАЦИИ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
- § 51. ГИПЕРФРАГМЕНТЫ (ИЛИ Л°-ЯДРА)
- § 52. НАРУШЕНИЕ ЗАКОНА СОХРАНЕНИЯ ЧЕТНОСТИ
- § 53. ФИЗИКА НЕЙТРИНО
- ГЛАВА ДЕВЯТАЯ. КОСМИЧЕСКИЕ ЛУЧИ
- § 54. ОТКРЫТИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
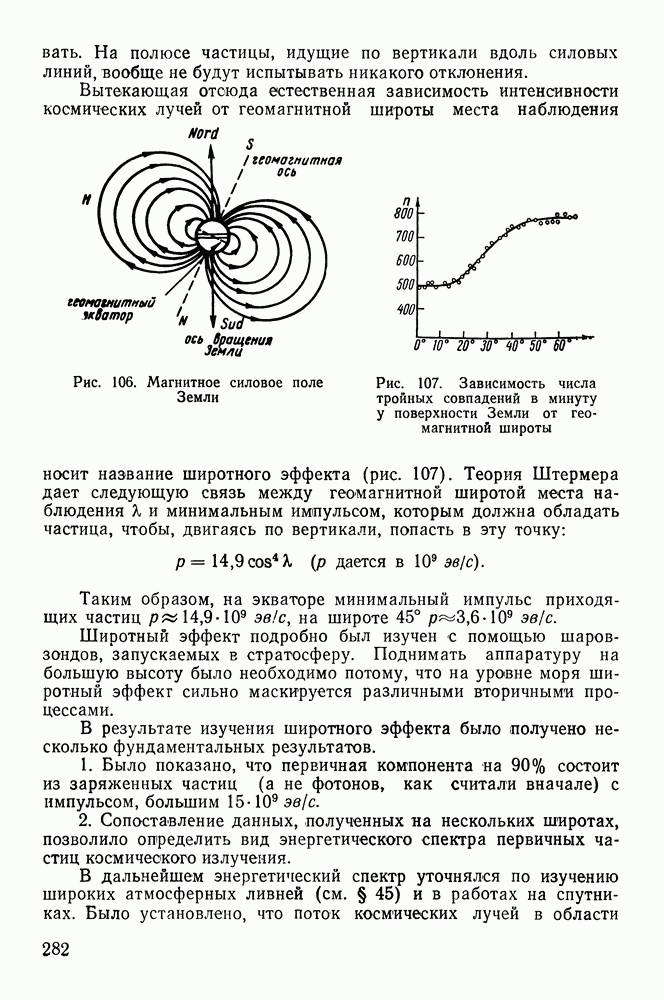
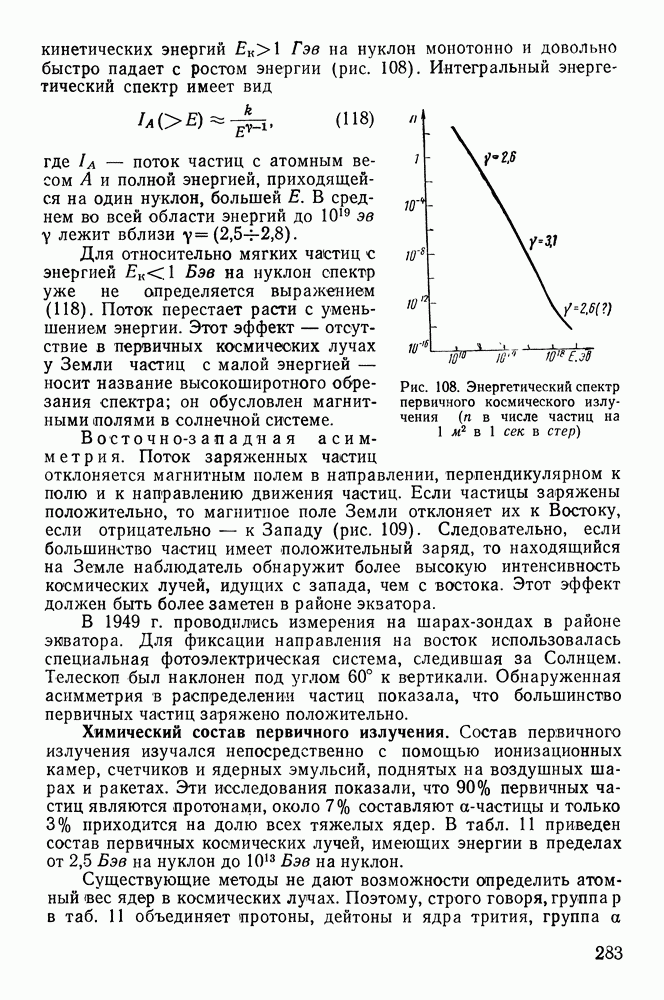
- § 55. ПЕРВИЧНОЕ ИЗЛУЧЕНИЕ У ЗЕМЛИ
- § 56. ВЗАИМОДЕЙСТВИЕ КОСМИЧЕСКОГО ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
- § 57. СОСТАВ КОСМИЧЕСКИХ ЛУЧЕЙ НА УРОВНЕ МОРЯ
- § 58. ВРЕМЕННЫЕ ИЗМЕНЕНИЯ ИНТЕНСИВНОСТИ КОСМИЧЕСКИХ ЛУЧЕЙ
- § 59. РАДИАЦИОННЫЕ ПОЯСА
- § 60. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА