| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
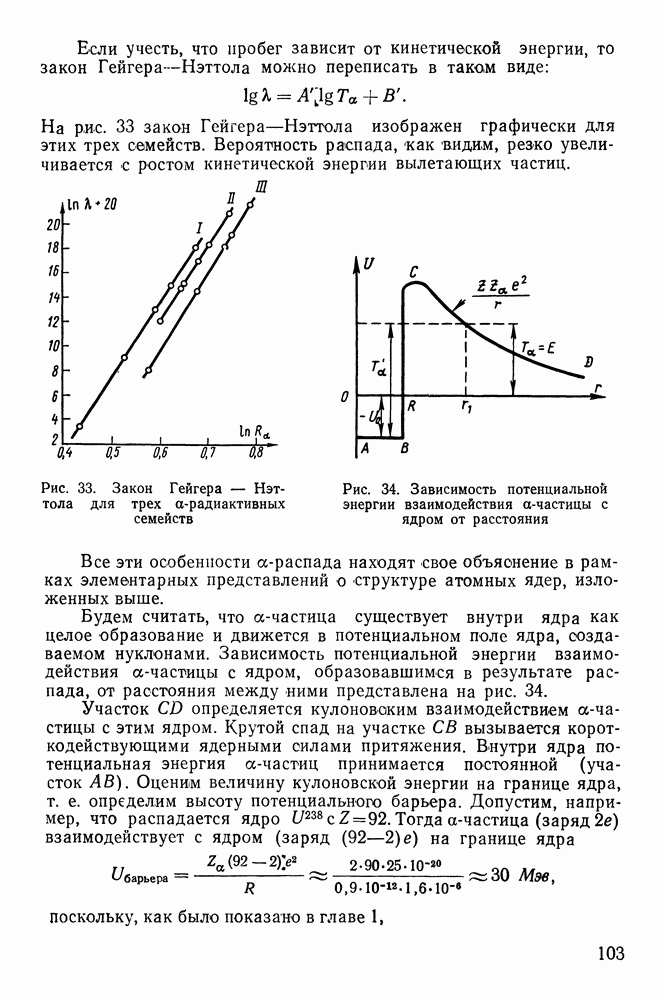
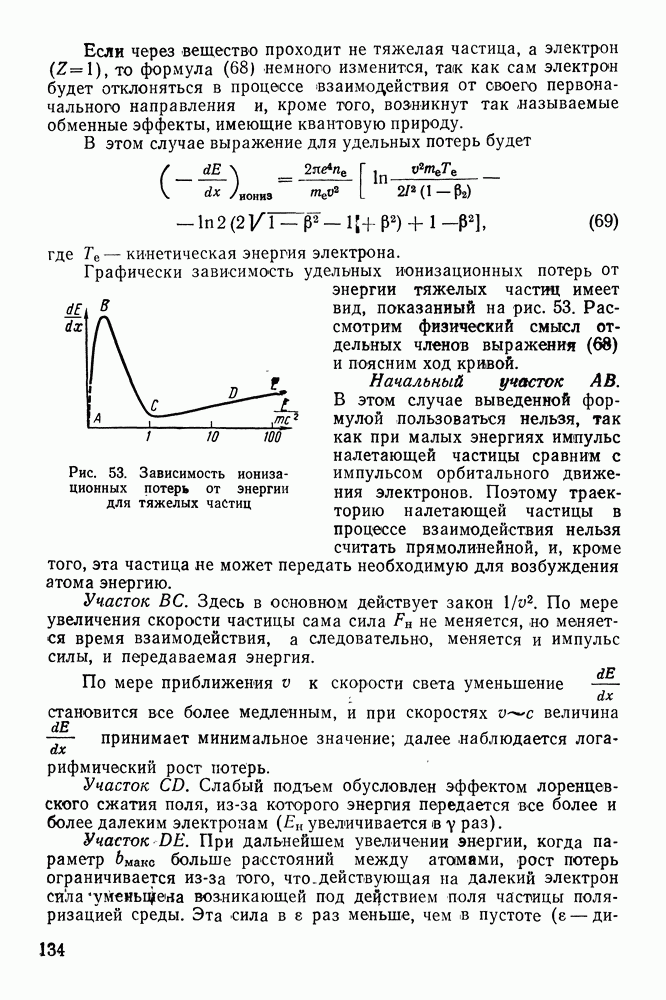
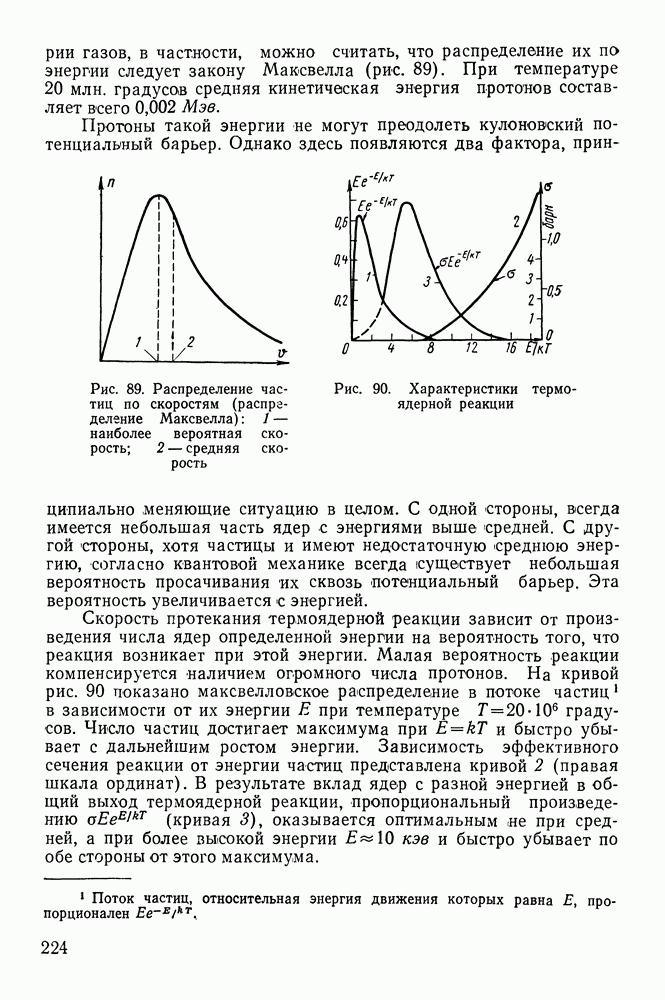
Пробег заряженных частиц в веществе.
Под пробегом частицы  в каком-нибудь веществе понимается толщина слоя этого вещества, которую может пройти частица с энергией
в каком-нибудь веществе понимается толщина слоя этого вещества, которую может пройти частица с энергией  до полной остановки, если направление ее движения было перпендикулярно поверхности слоя.
до полной остановки, если направление ее движения было перпендикулярно поверхности слоя.
По существу эта величина более или менее определенна лишь для тяжелых частиц, путь которых практически является прямой линией; и по этой причине разброс в величине пробега для частиц одинаковой энергии невелик. У легких частиц, например у электронов малых энергий, вероятность рассеяния велика «и поэтому понятие пути и понятие пробега для них не совпадают. По измеренному пробегу частицы в среде можно определять ее энергию, или, зная зависимость величины пробега от энергии, определять массу частицы.
Для данной среды и для частицы с зарядом  величина удельных потерь является функцией только скорости, а следовательно, у частицы с известной массой — функцией только кинетической энергии
величина удельных потерь является функцией только скорости, а следовательно, у частицы с известной массой — функцией только кинетической энергии

Зная вид функции  можно найти и полный пробег частицы
можно найти и полный пробег частицы

Для нерелятивистских энергий  можно записать
можно записать 

Подставив (72) и (73) в (71) и произведя интегрирование, получим

Из этого соотношения следует, что:
1) при равных скоростях пробеги заряженных частиц в веществе пропорциональны массам этих частиц и обратно пропорциональны квадратам зарядов:

2) при равных энергиях частиц их пробеги обратно пропорциональны массам:

Пробеги заряженных частиц часто выражают в 

и пользуются выражением удельных потерь в форме:

Измерять пробеги в  удобно, потому что удельные ионизационные потери в легких веществах, рассчитанные на
удобно, потому что удельные ионизационные потери в легких веществах, рассчитанные на  одинаковы в разных средах. Действительно, мы видели, что
одинаковы в разных средах. Действительно, мы видели, что  и, следовательно,
и, следовательно,

Однако число электронов, содержащихся в  вещества, равно
вещества, равно

где  число Авагадро, А — атомный вес вещества.
число Авагадро, А — атомный вес вещества.
Так как у легких элементов  то в слое любого легкого вещества толщиной
то в слое любого легкого вещества толщиной  будет содержаться примерно
будет содержаться примерно  электронов:
электронов:

а это означает, что

Для однозарядных релятивистских частиц

и слабо убывает с ростом  вещества.
вещества.
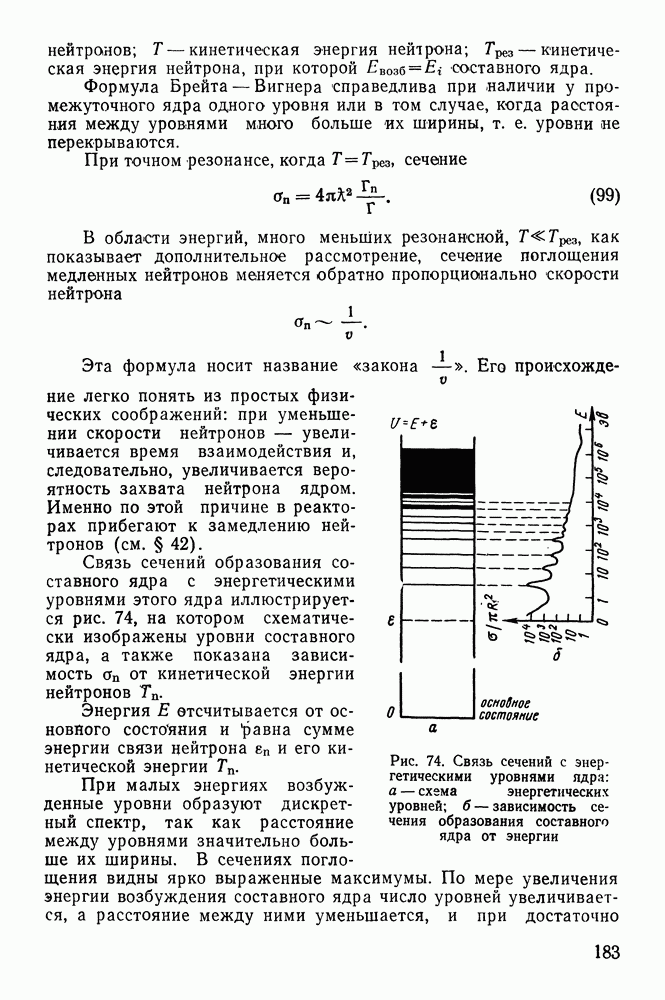
На основании формулы для пробега чистиц (74), примененной к однородному пучку, который проходит слой поглотителя без
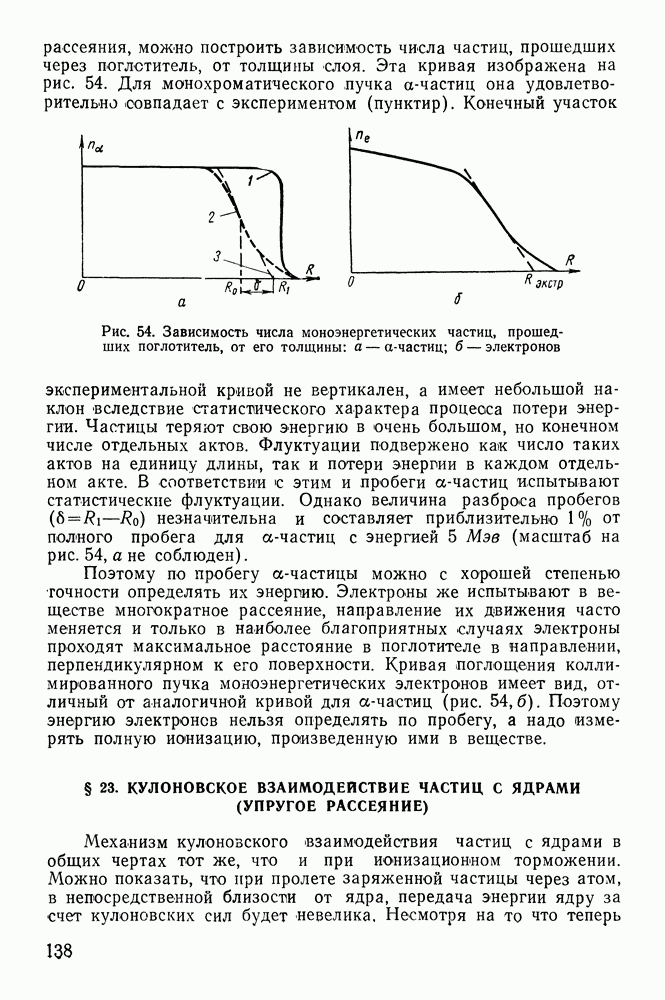
рассеяния, можно построить зависимость числа частиц, прошедших через поглотитель, от толщины слоя. Эта кривая изображена на рис. 54. Для монохроматического пучка  -частиц она удовлетворительно совпадает с экспериментом (пунктир).
-частиц она удовлетворительно совпадает с экспериментом (пунктир).

Рис. 54. Зависимость числа моноэнергетических частиц, прошедших поглотитель, от его толщины: а —  -частиц;
-частиц;  электронов
электронов
Конечный участок экспериментальной кривой не вертикален, а имеет небольшой наклон вследствие статистического характера процесса потери энергии. Частицы теряют свою энергию в очень большом, но конечном числе отдельных актов. Флуктуации подвержено как число таких актов на единицу длины, так и потери энергии в каждом отдельном акте. В соответствии с этим и пробеги  -частиц испытывают статистические флуктуации. Однако величина разброса пробегов
-частиц испытывают статистические флуктуации. Однако величина разброса пробегов  незначительна и составляет приблизительно 1% от полного пробега для
незначительна и составляет приблизительно 1% от полного пробега для  -частиц с энергией
-частиц с энергией  (масштаб на рис. 54, а не соблюден).
(масштаб на рис. 54, а не соблюден).
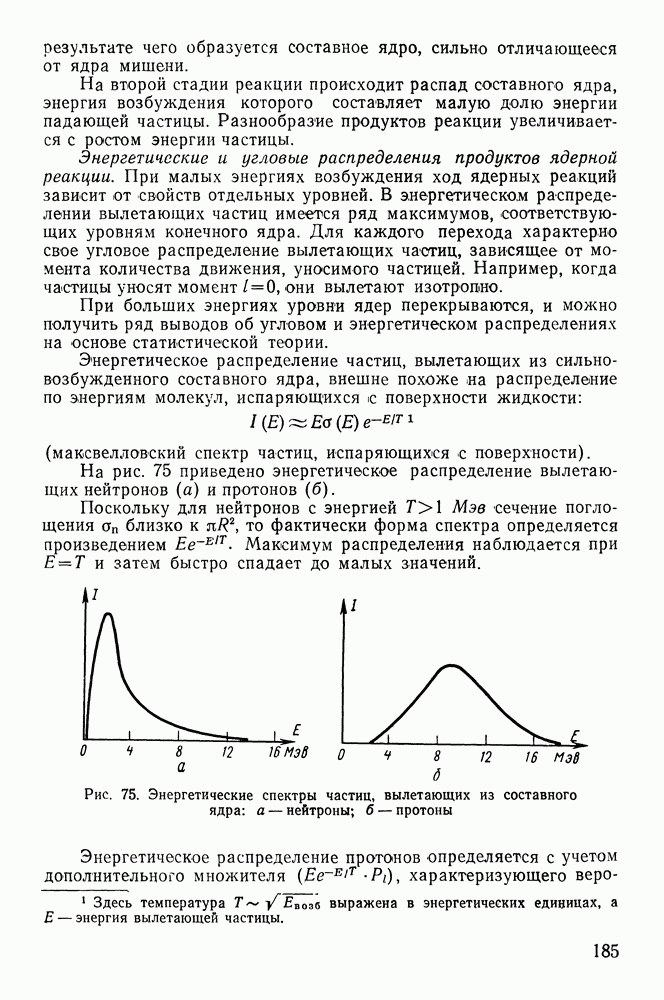
Поэтому по пробегу  -частицы можно с хорошей степенью точности определять их энергию. Электроны же испытывают в веществе многократное рассеяние, направление их движения часто меняется и только в наиболее благоприятных случаях электроны проходят максимальное расстояние в поглотителе в направлении, перпендикулярном к его поверхности. Кривая поглощения коллимированного пучка моноэнергетических электронов имеет вид, отличный от аналогичной кривой для
-частицы можно с хорошей степенью точности определять их энергию. Электроны же испытывают в веществе многократное рассеяние, направление их движения часто меняется и только в наиболее благоприятных случаях электроны проходят максимальное расстояние в поглотителе в направлении, перпендикулярном к его поверхности. Кривая поглощения коллимированного пучка моноэнергетических электронов имеет вид, отличный от аналогичной кривой для  -частиц (рис. 54,б). Поэтому энергию электронов нельзя определять по пробегу, а надо измерять полную ионизацию, произведенную ими в веществе.
-частиц (рис. 54,б). Поэтому энергию электронов нельзя определять по пробегу, а надо измерять полную ионизацию, произведенную ими в веществе.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Масштабы физических величин.
- Особенности физических явлений в микромире.
- РАЗДЕЛ ПЕРВЫЙ. СТАБИЛЬНЫЕ ЯДРА И ЯДЕРНЫЕ СИЛЫ
- § 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ПРОТОНА И НЕЙТРОНА
- § 2. ЗАРЯД АТОМНОГО ЯДРА
- § 3. РАЗМЕРЫ АТОМНЫХ ЯДЕР
- § 4. ЭНЕРГИЯ СВЯЗИ ЯДРА
- § 5. МАССА И ЭНЕРГИЯ
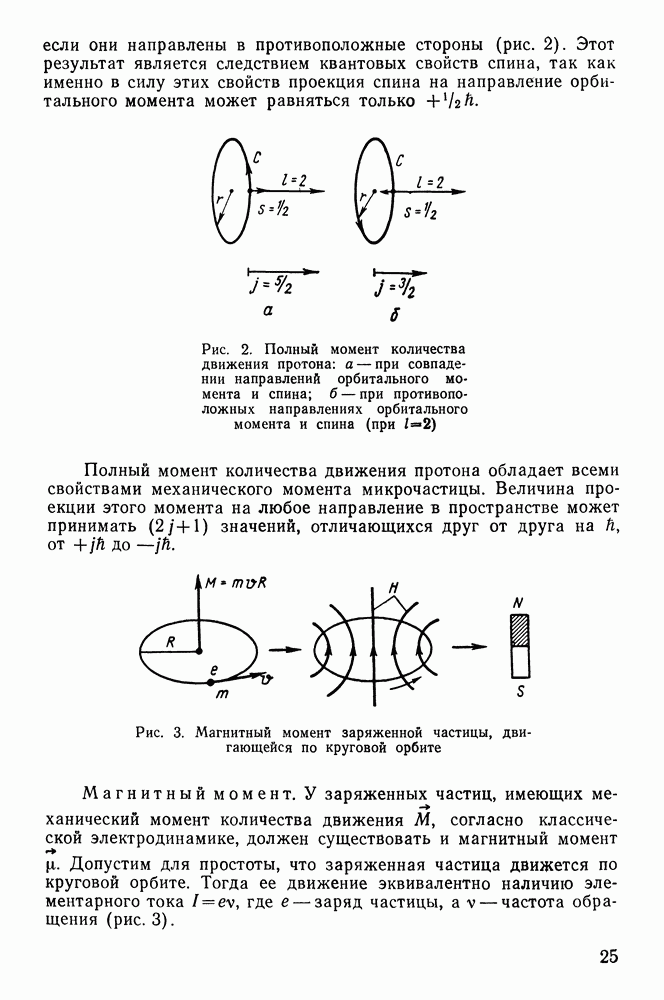
- § 6. СПИН И МАГНИТНЫЙ МОМЕНТ ЯДРА
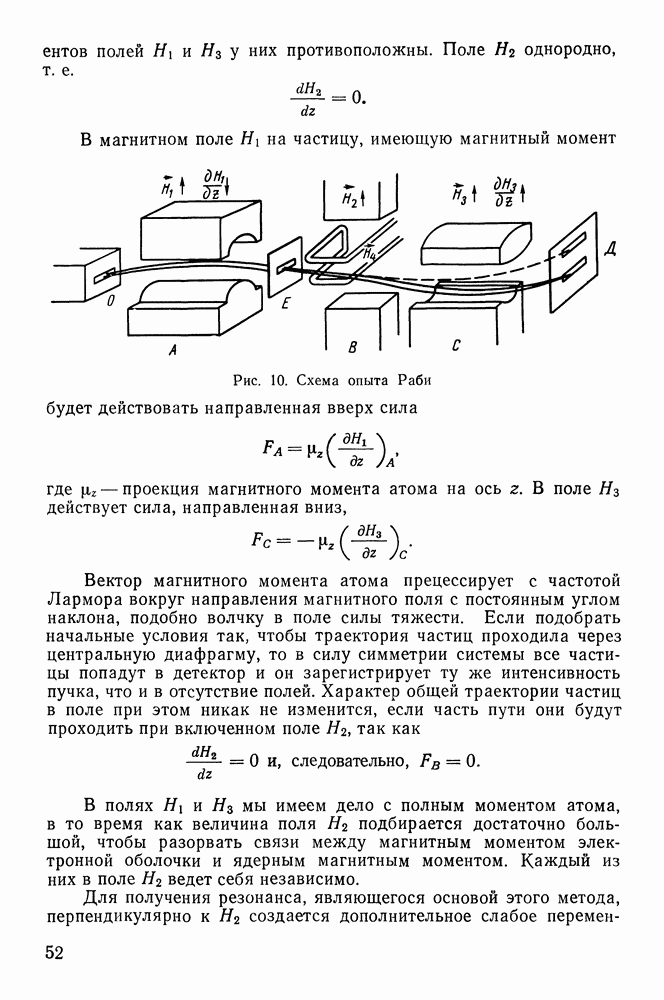
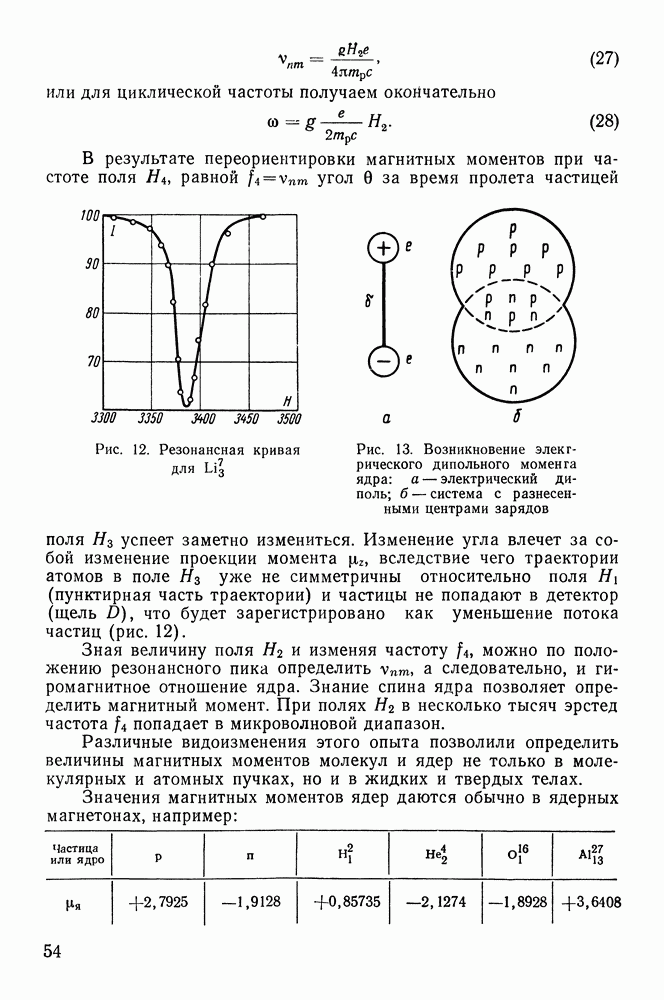
- Методы определения спинов и магнитных моментов ядер.
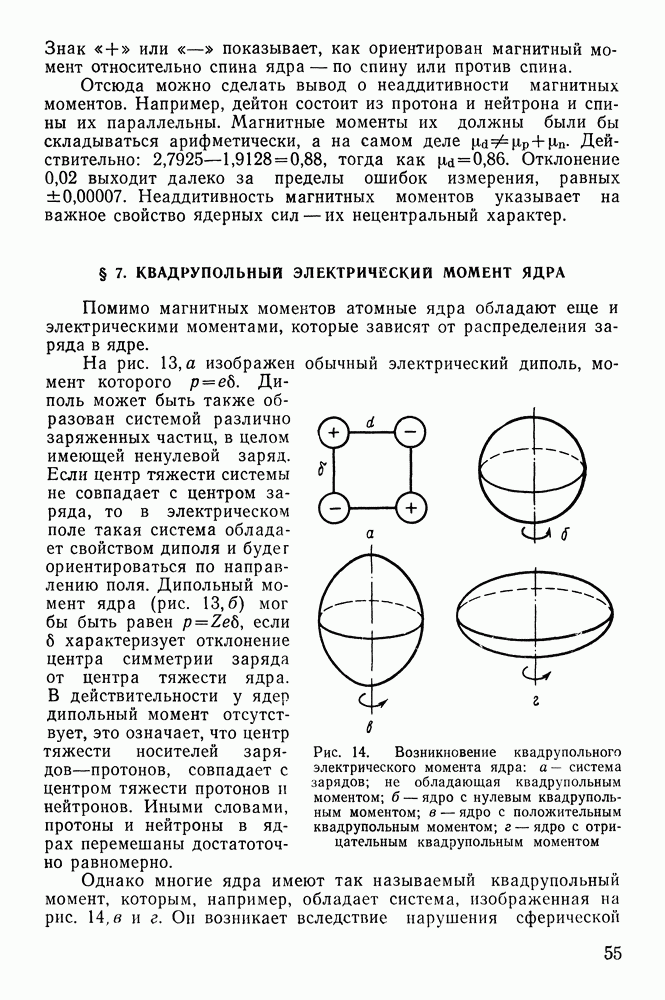
- § 7. КВАДРУПОЛЬНЫЙ ЭЛЕКТРИЧЕСКИЙ МОМЕНТ ЯДРА
- § 8. ЧЕТНОСТЬ ВОЛНОВОЙ ФУНКЦИИ
- § 9. ЯДЕРНЫЕ МОДЕЛИ
- Глава вторая. ЯДЕРНЫЕ СИЛЫ
- § 10. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДЕРНЫХ СИЛ
- § 11. ФИЗИЧЕСКИЕ ОБОСНОВАНИЯ МЕЗОННОИ ТЕОРИИ ЯДЕРНЫХ СИЛ
- § 12. СТРУКТУРА НУКЛОНА
- § 13. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДЕЙТОНА
- Магнитный момент дейтона.
- РАЗДЕЛ ВТОРОЙ. НЕУСТОЙЧИВЫЕ ЯДРА
- § 14. ОТКРЫТИЕ РАДИОАКТИВНОСТИ
- § 15. ЗАКОНЫ РАДИОАКТИВНОГО РАСПАДА
- § 16. ТРАНСУРАНОВЫЕ ЭЛЕМЕНТЫ
- § 17. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ ИЗОТОПОВ
- § 18. АЛЬФА-РАСПАД
- § 19. БЕТА-РАСПАД
- Энергетические спектры электронов при b-распаде и роль нейтрино.
- Энергетические соотношения при b-распаде.
- § 20. ГАММА-ИЗЛУЧЕНИЕ ЯДЕР
- Ядерная изомерия.
- Эффект Мёссбауера.
- ГЛАВА ЧЕТВЕРТАЯ. ВЗАИМОДЕЙСТВИЕ ЯДЕРНОГО ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
- § 21. ВИДЫ ВЗАИМОДЕЙСТВИЯ
- § 22. ВЗАИМОДЕЙСТВИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ СО СРЕДОЙ
- Пробег заряженных частиц в веществе.
- § 23. КУЛОНОВСКОЕ ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ С ЯДРАМИ (УПРУГОЕ РАССЕЯНИЕ)
- § 24. ЯДЕРНОЕ ВЗАИМОДЕЙСТВИЕ
- § 25. ИЗЛУЧЕНИЕ ВАВИЛОВА — ЧЕРЕНКОВА
- § 26. ПРОХОЖДЕНИЕ ГАММА-ИЗЛУЧЕНИЯ ЧЕРЕЗ ВЕЩЕСТВО
- Рассеяние y-лучей. Эффект Комптона.
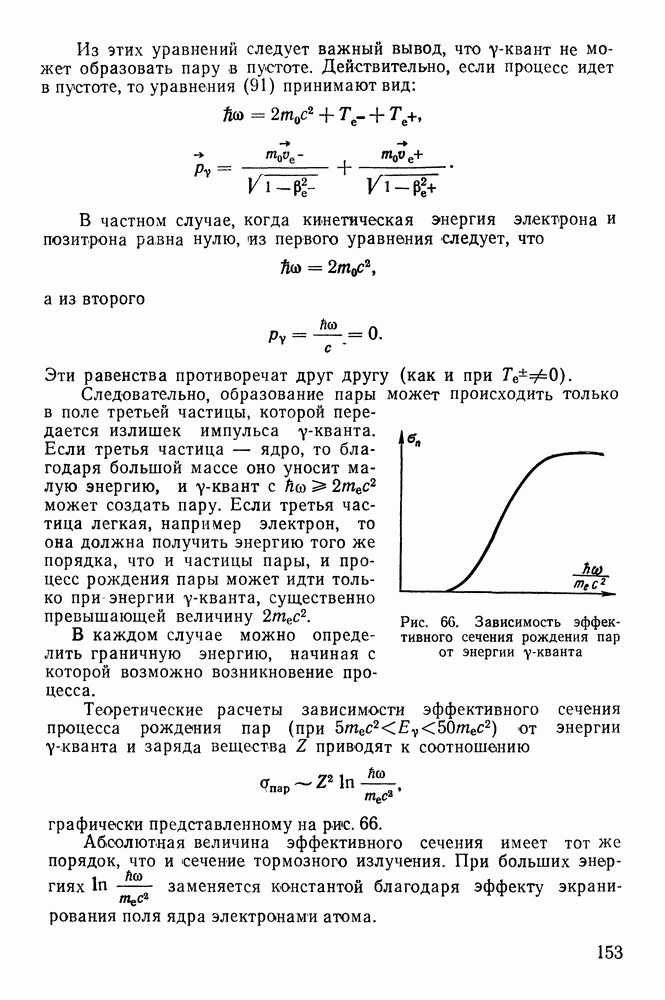
- Рождение электронно-позитронных пар.
- Другие эффекты, возникающие при поглощении y-лучей
- Суммарный коэффициент поглощения y-излучения
- Процесс аннигиляции электронно-позитронных пар.
- § 27. МЕТОДЫ РЕГИСТРАЦИИ ИЗЛУЧЕНИЯ
- РАЗДЕЛ ТРЕТИЙ. ЯДЕРНЫЕ РЕАКЦИИ
- ГЛАВА ПЯТАЯ. ЗАКОНОМЕРНОСТИ ЯДЕРНЫХ РЕАКЦИЙ
- § 29. ЗАКОНЫ СОХРАНЕНИЯ В ЯДЕРНЫХ РЕАКЦИЯХ
- § 30. РАЗЛИЧНЫЕ МЕХАНИЗМЫ РЕАКЦИЙ
- ГЛАВА ШЕСТАЯ. ФИЗИКА НЕЙТРОНОВ
- § 31. ОТКРЫТИЕ НЕЙТРОНА И ЕГО СВОЙСТВА
- § 32. ИСТОЧНИКИ НЕЙТРОНОВ
- § 33. ВЗАИМОДЕЙСТВИЕ НЕЙТРОНОВ С ВЕЩЕСТВОМ
- § 34. МЕТОДЫ РЕГИСТРАЦИИ НЕЙТРОНОВ
- § 35. ЗАМЕДЛЕНИЕ НЕЙТРОНОВ
- § 36. МЕТОДЫ ПОЛУЧЕНИЯ МОНОХРОМАТИЧЕСКИХ НЕЙТРОНОВ
- ГЛАВА СЕДЬМАЯ. ДЕЛЕНИЕ И СИНТЕЗ ЯДЕР
- § 37. ОТКРЫТИЕ ДЕЛЕНИЯ ЯДЕР
- § 38. ПРОЦЕССЫ, ПРОИСХОДЯЩИЕ ПРИ ДЕЛЕНИИ ЯДЕР УРАНА
- § 39. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДЕЛЕНИЯ
- § 40. ТИПЫ РЕАКЦИЙ ДЕЛЕНИЯ
- § 41. ВОЗМОЖНОСТЬ ИСПОЛЬЗОВАНИЯ ЯДЕРНОЙ ЭНЕРГИИ
- § 42. ЦЕПНАЯ ЯДЕРНАЯ РЕАКЦИЯ И ЯДЕРНЫЕ РЕАКТОРЫ
- § 43. ТЕРМОЯДЕРНЫЙ СИНТЕЗ
- Термоядерные реакции в лабораторных условиях.
- РАЗДЕЛ ЧЕТВЕРТЫЙ. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И КОСМИЧЕСКИЕ ЛУЧИ
- § 44. ОТКРЫТИЕ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
- § 45. ВИДЫ ВЗАИМОДЕЙСТВИЯ ЧАСТИЦ
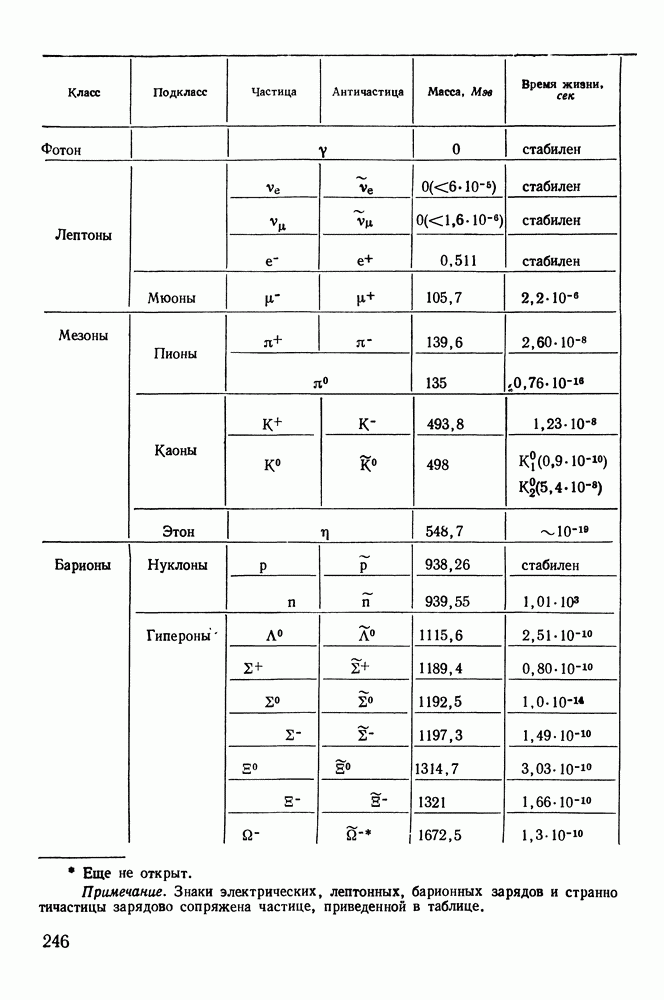
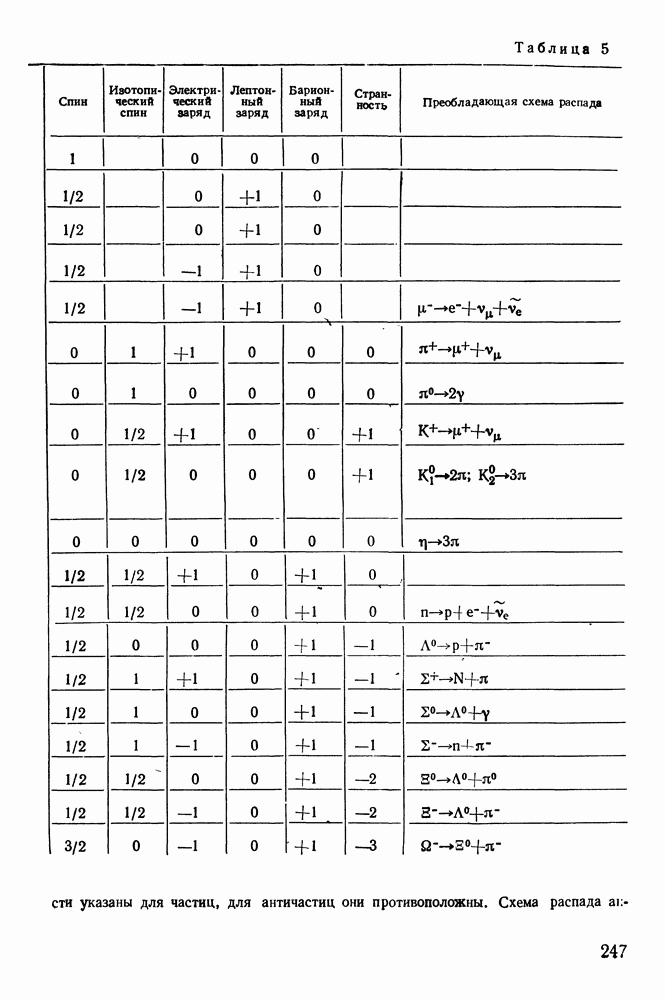
- § 46. КЛАССИФИКАЦИЯ ЧАСТИЦ
- § 47. РЕАКЦИИ МЕЖДУ ЧАСТИЦАМИ
- § 48. ВНУТРЕННИЕ СВОЙСТВА ЧАСТИЦ
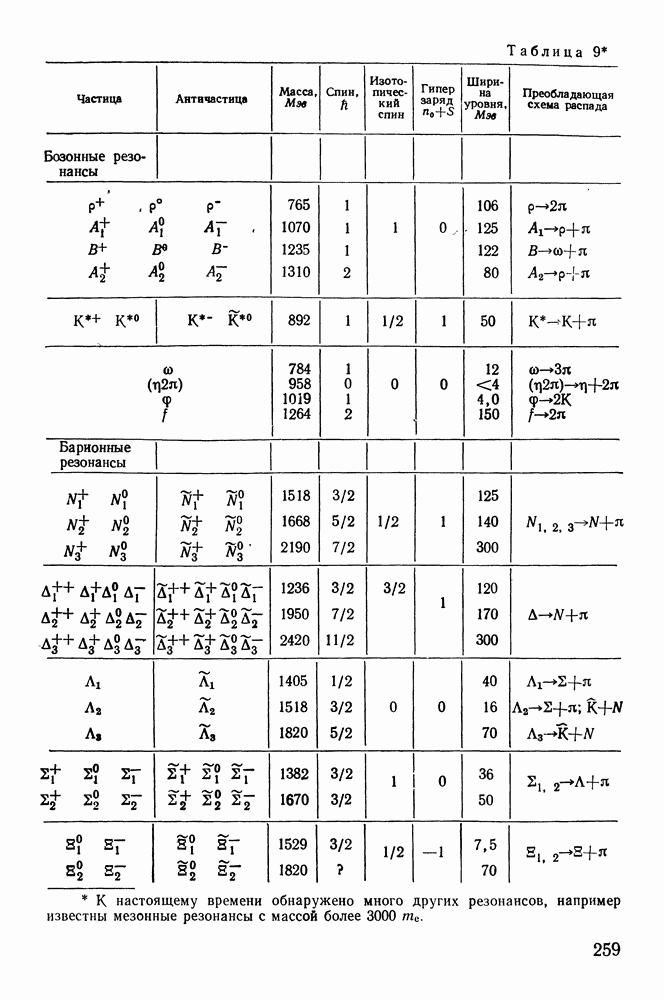
- § 49. РЕЗОНАНСЫ
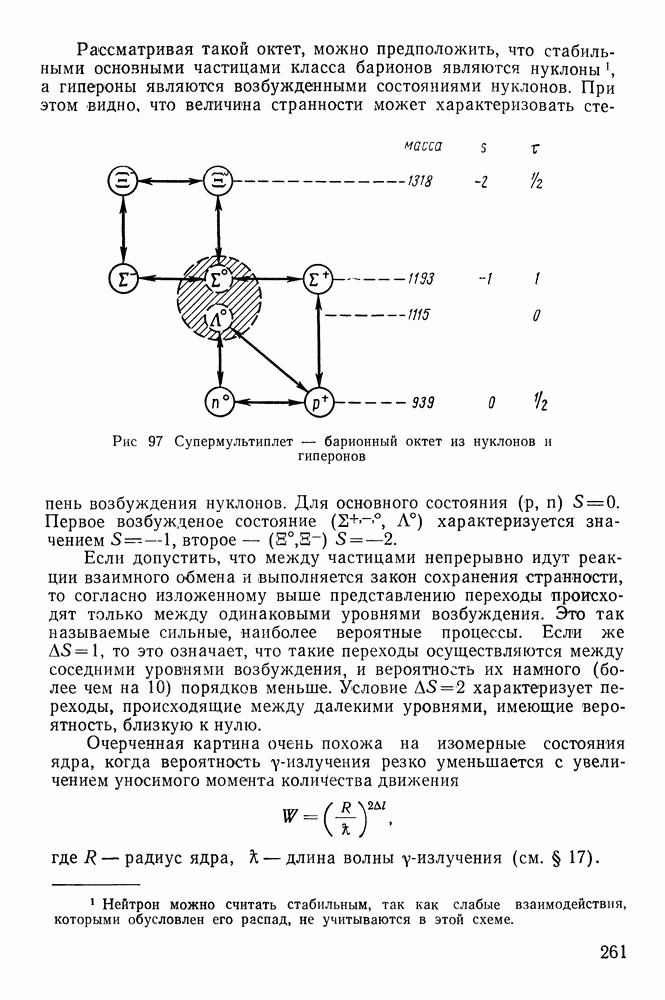
- § 50. ПОПЫТКИ СИСТЕМАТИЗАЦИИ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
- § 51. ГИПЕРФРАГМЕНТЫ (ИЛИ Л°-ЯДРА)
- § 52. НАРУШЕНИЕ ЗАКОНА СОХРАНЕНИЯ ЧЕТНОСТИ
- § 53. ФИЗИКА НЕЙТРИНО
- ГЛАВА ДЕВЯТАЯ. КОСМИЧЕСКИЕ ЛУЧИ
- § 54. ОТКРЫТИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- § 55. ПЕРВИЧНОЕ ИЗЛУЧЕНИЕ У ЗЕМЛИ
- § 56. ВЗАИМОДЕЙСТВИЕ КОСМИЧЕСКОГО ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
- § 57. СОСТАВ КОСМИЧЕСКИХ ЛУЧЕЙ НА УРОВНЕ МОРЯ
- § 58. ВРЕМЕННЫЕ ИЗМЕНЕНИЯ ИНТЕНСИВНОСТИ КОСМИЧЕСКИХ ЛУЧЕЙ
- § 59. РАДИАЦИОННЫЕ ПОЯСА
- § 60. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА