| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 22. ВЗАИМОДЕЙСТВИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ СО СРЕДОЙ
Ионизационное торможение заряженных частиц. При электромагнитном взаимодействии быстрых заряженных частиц с электронами вещества последние переходят в возбужденное состояние; когда они остаются внутри атома, происходит возбуждение атома, и спектр этих состояний имеет дискретный характер; в тех случаях. когда электроны вырываются из атома, их энергия может иметь любые значения, а атом при этом ионизуется. Увеличение энергии электрона происходит за счет кинетической энергии падающей частицы. В обоих случаях для краткости принято говорить, что энергия летящей частицы убывает вследствие ионизационных потерь.
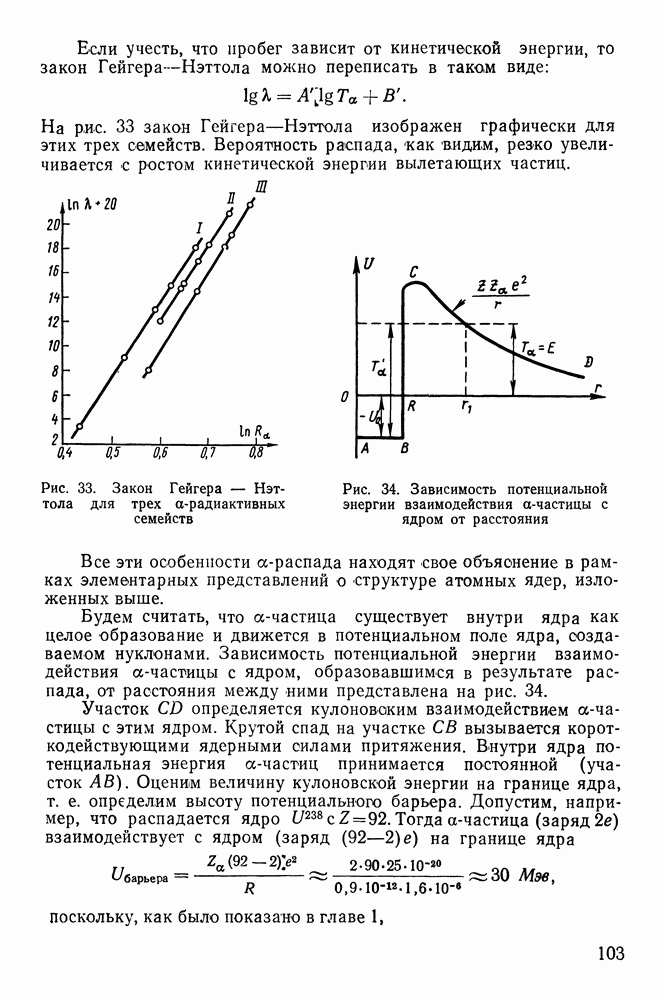
Рассмотрим взаимодействие тяжелой заряженной частицы с электроном. Такая частица ничтожно отклоняется со своего прямолинейного пути и этим отклонением можно пренебречь. Допустим, что частица с зарядом  массой
массой  и скоростью
и скоростью  пролетает на расстоянии
пролетает на расстоянии  от электрона, где
от электрона, где  прицельный параметр, или параметр удара (рис. 51). Взаимодействие частицы с электроном
прицельный параметр, или параметр удара (рис. 51). Взаимодействие частицы с электроном
приведет к тому, что электрон получит импульс в направлении, перпендикулярном к линии полета частицы

где  электростатическая сила и
электростатическая сила и  ее составляющая нормальная к линии полета, а
ее составляющая нормальная к линии полета, а  время взаимодействия.
время взаимодействия.

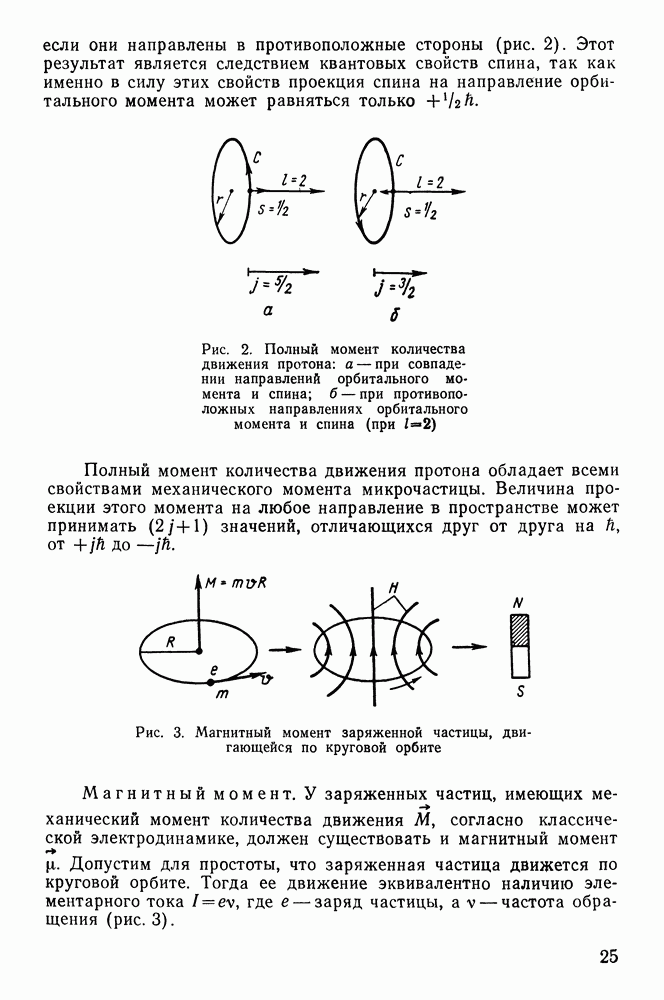
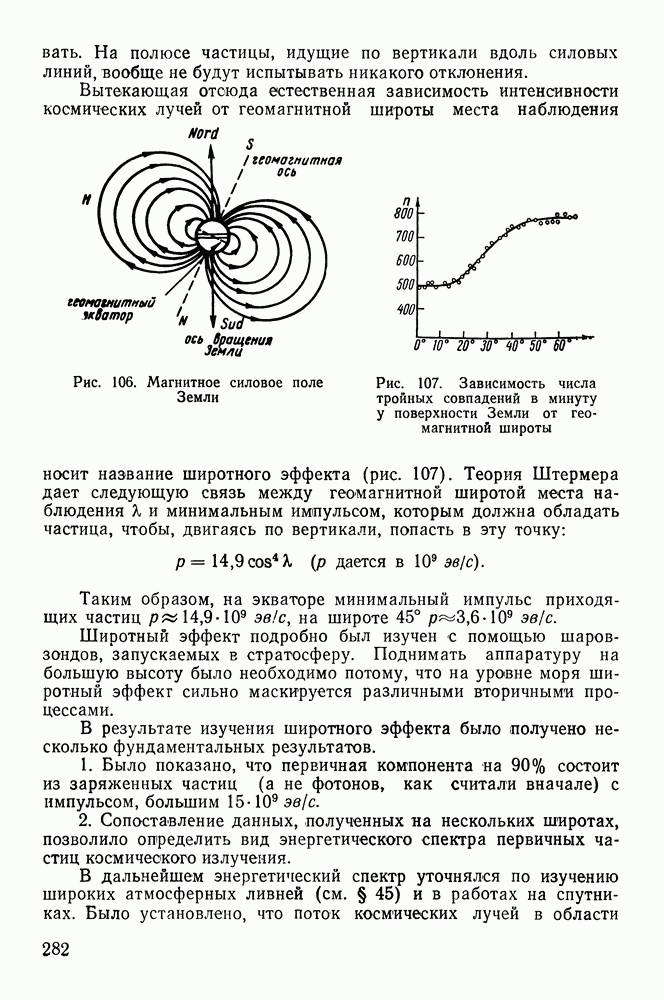
Рис. 51. Взаимодействие заряженной частицы с электроном атома

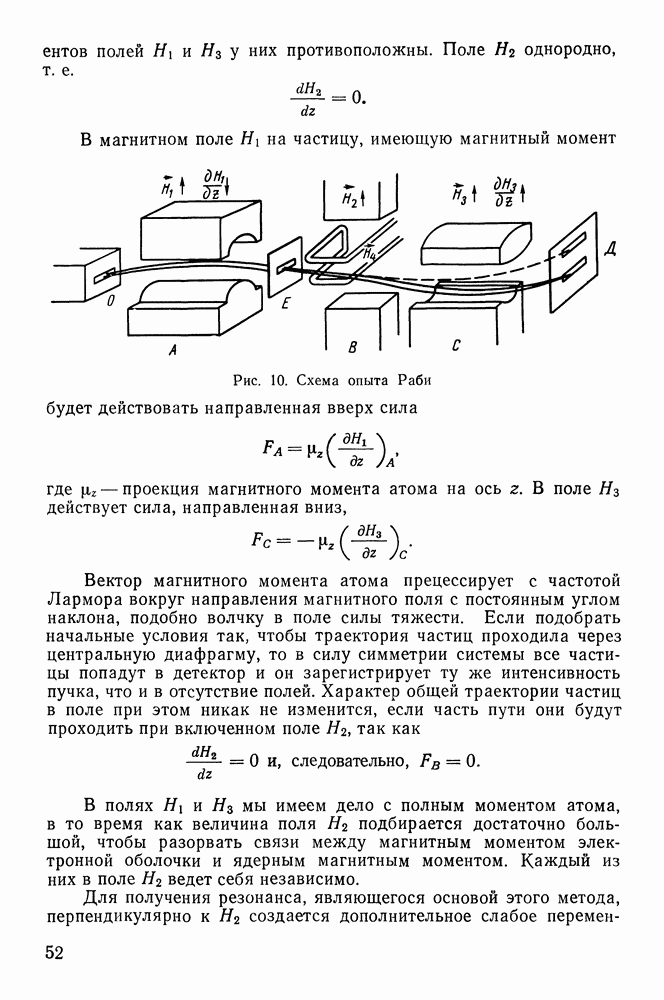
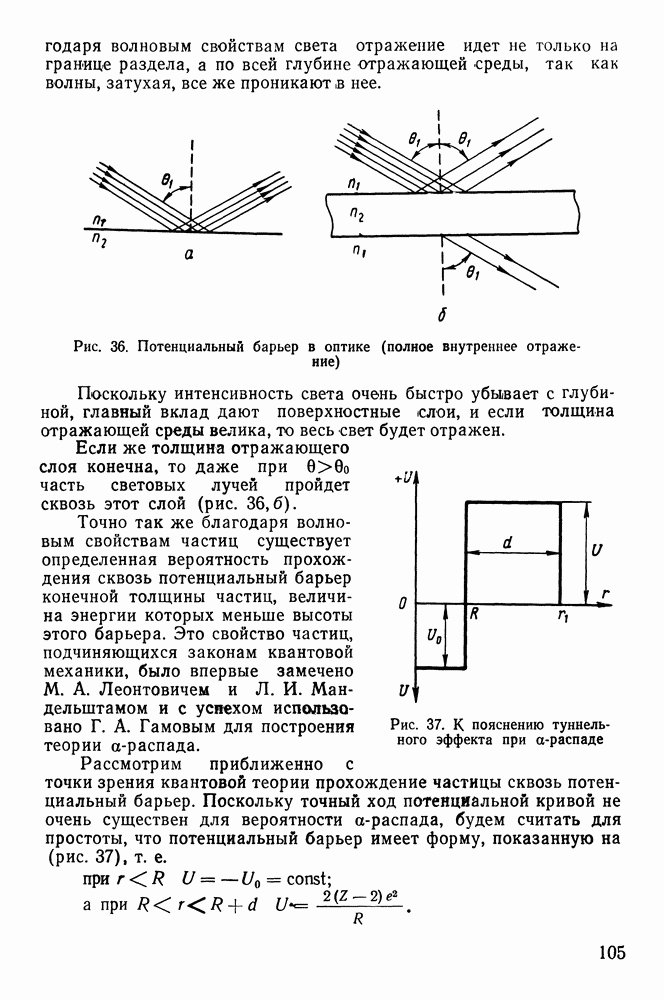
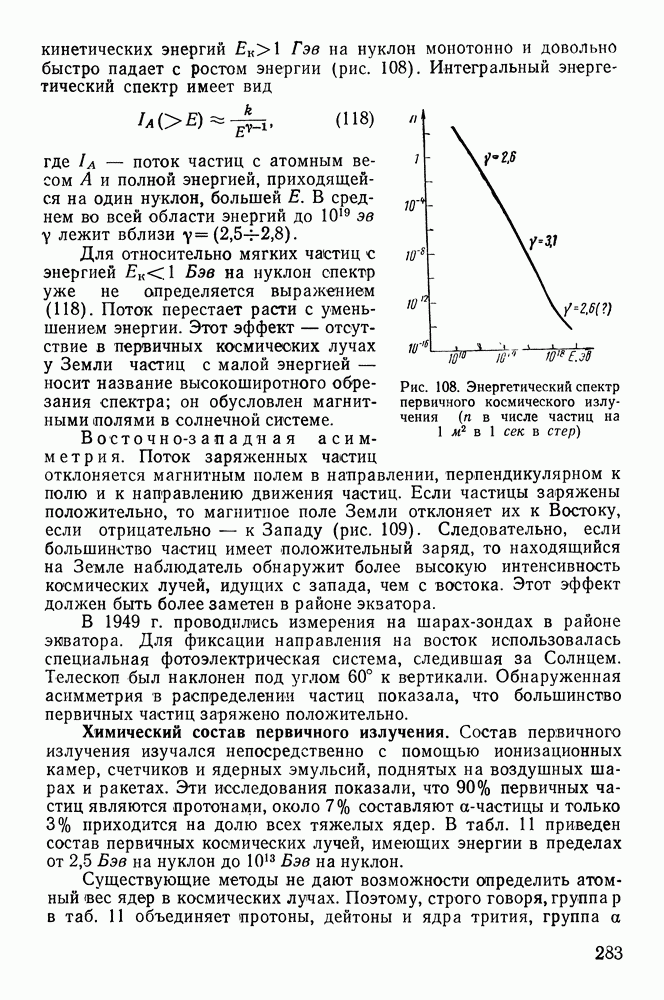
Рис. 52. К расчету ионизационных потерь
Импульс же, полученный в продольном направлении  как легко видеть, равен нулю, так как продольная компонента силы на пути до точки наибольшего сближения и после нее имеет противоположные знаки.
как легко видеть, равен нулю, так как продольная компонента силы на пути до точки наибольшего сближения и после нее имеет противоположные знаки.
Если считать, что взаимодействие существенно только на некотором отрезке пути 2b, то время пролета определится как  Кулоновская сила на этом участке по порядку величины
Кулоновская сила на этом участке по порядку величины  , и поэтому импульс, полученный электроном, может быть записан как
, и поэтому импульс, полученный электроном, может быть записан как

а переданная электрону энергия

Эту энергию в среднем и теряет заряженная частица.
Чтобы учесть все электроны с данным параметром удара, рассмотрим кольцевой цилиндр, ось которого совпадает с траекторией частицы, а боковая поверхность проходит через точку, где находится электрон (рис. 52).
Бели число электронов в  вещества равно то между стенками цилиндров радиусов
вещества равно то между стенками цилиндров радиусов  т. е. в объеме
т. е. в объеме 
(единичной длины), будет находиться  электронов. В результате взаимодействия с ними заряженная частица на длине
электронов. В результате взаимодействия с ними заряженная частица на длине  потеряет энергию
потеряет энергию

Для получения полных ионизационных потерь нужно проинтегрировать (66) по всем возможным значениям параметра удара от минимального  до максимального
до максимального  что дает
что дает

Пределы  выбирают из физических соображений поразному в релятивистском и нерелятивистском случаях. Так как они входят под знак логарифма, то особая точность в их определении не требуется. При классическом рассмотрении значение
выбирают из физических соображений поразному в релятивистском и нерелятивистском случаях. Так как они входят под знак логарифма, то особая точность в их определении не требуется. При классическом рассмотрении значение  определяется исходя из максимальной энергии, которая может быть йередана электрону в атоме. Такая максимальная энергия передается при лобовом столкновении и равна
определяется исходя из максимальной энергии, которая может быть йередана электрону в атоме. Такая максимальная энергия передается при лобовом столкновении и равна  . Подставив это значение в (65), получим
. Подставив это значение в (65), получим

Учет квантовомеханических эффектов приводит к несколько иному выражению

Предел бмакс определяется из энергии связи электрона в атоме, ибо при передаче энергии, меньшей характерной энергий возбуждения атома, возбуждение его вообще не произойдет.
В релятивистском случае нужно учесть, что поле падающей частицы сжимается в направлении движения, а величина  увеличивается в у раз, где
увеличивается в у раз, где  Это приводит к тому, что энергия будет передаваться также и более удаленным электронам
Это приводит к тому, что энергия будет передаваться также и более удаленным электронам

где I — средний ионизационный потенциал атомов поглощающего вещества.
Точный подсчет дает окончательно для ионизационных потерь энергии тяжелой частицей

Если через вещество проходит не тяжелая частица, а электрон  то формула (68) немного изменится, так: как сам электрон будет отклоняться в процессе взаимодействия от своего первоначального направления и, кроме того, возникнут так называемые обменные эффекты, имеющие квантовую природу.
то формула (68) немного изменится, так: как сам электрон будет отклоняться в процессе взаимодействия от своего первоначального направления и, кроме того, возникнут так называемые обменные эффекты, имеющие квантовую природу.
В этом случае выражение для удельных потерь будет

где  кинетическая энергия электрона.
кинетическая энергия электрона.
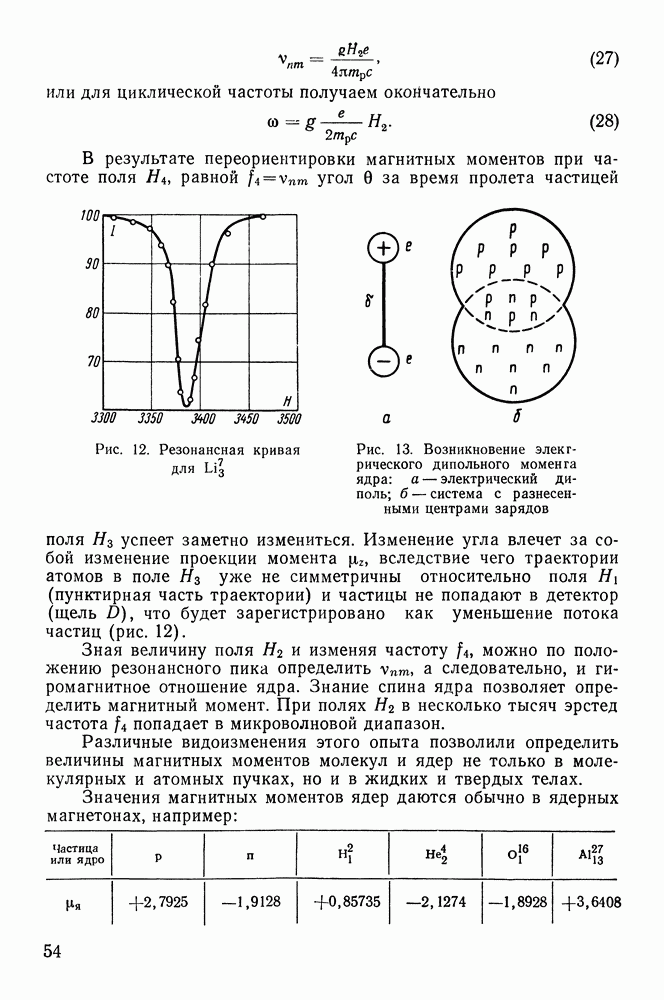
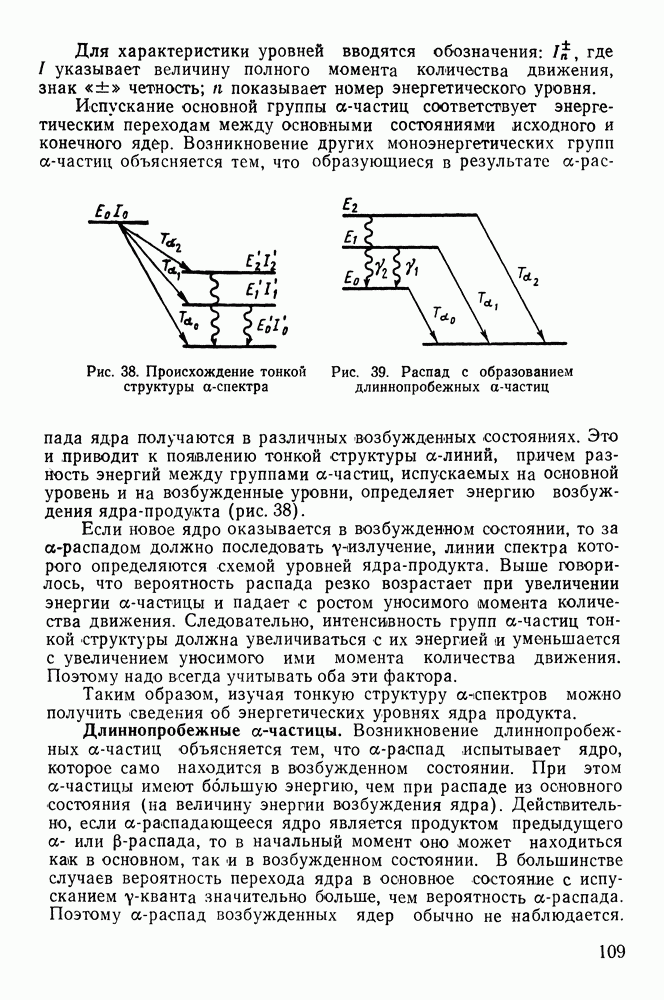
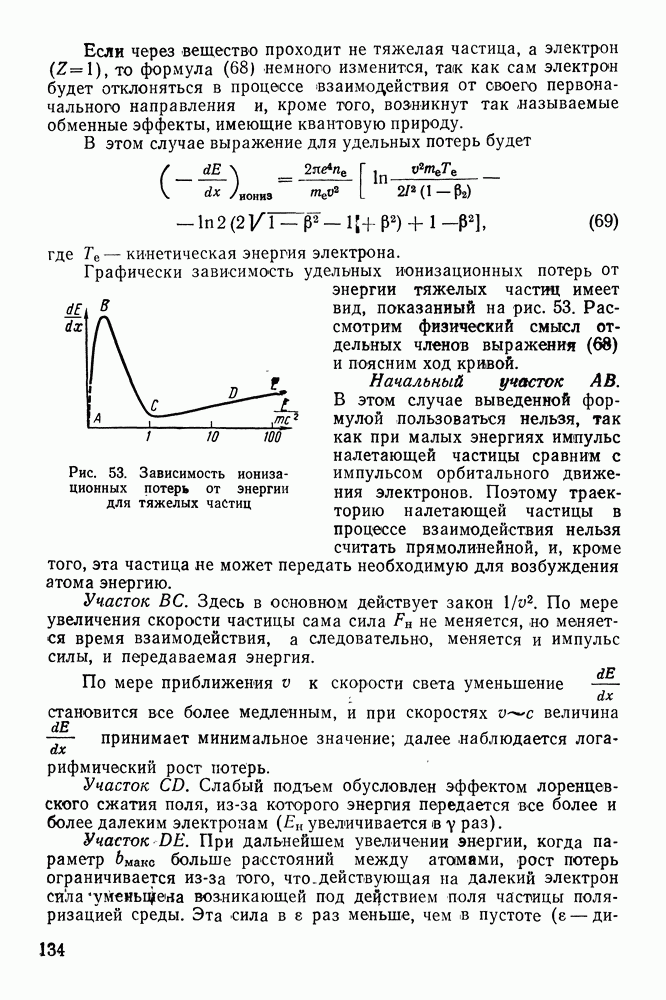
Графически зависимость удельных ионизационных потерь от энергии тяжелых частиц имеет вид, показанный на рис. 53. Рассмотрим физический смысл отдельных членов выражения (68) и поясним ход кривой.

Рис. 53. Зависимость ионизационных потерь от энергии для тяжелых частиц
Начальный учосток  . В этом случае выведенной формулой пользоваться нельзя, так как при малых энергиях импульс налетающей частицы сравним с импульсом орбитального движения электронов. Поэтому траекторию налетающей частицы в процессе взаимодействия нельзя считать прямолинейной, и, кроме того, эта частица не может передать необходимую для возбуждения атома энергию.
. В этом случае выведенной формулой пользоваться нельзя, так как при малых энергиях импульс налетающей частицы сравним с импульсом орбитального движения электронов. Поэтому траекторию налетающей частицы в процессе взаимодействия нельзя считать прямолинейной, и, кроме того, эта частица не может передать необходимую для возбуждения атома энергию.
Участок  Здесь в основном действует закон
Здесь в основном действует закон  По мере увеличения скорости частицы сама сила
По мере увеличения скорости частицы сама сила  не меняется, но меняется время взаимодействия, а следовательно, меняется и импульс силы, и передаваемая энергия.
не меняется, но меняется время взаимодействия, а следовательно, меняется и импульс силы, и передаваемая энергия.
По мере приближения  к скорости света уменьшение
к скорости света уменьшение  становится все более медленным, и при скоростях величина
становится все более медленным, и при скоростях величина  принимает минимальное значение; далее наблюдается логарифмический рост потерь.
принимает минимальное значение; далее наблюдается логарифмический рост потерь.
Участок  Слабый подъем обусловлен эффектом лоренцевского сжатия поля, из-за которого энергия передается все более и более далеким электронам
Слабый подъем обусловлен эффектом лоренцевского сжатия поля, из-за которого энергия передается все более и более далеким электронам  увеличивается в у раз).
увеличивается в у раз).
Участок  При дальнейшем увеличении энергии, когда параметр бмакс больше расстояний между атомами, рост потерь ограничивается из-за того, что действующая на далекий электрон сила уменьшена возникающей под действием поля частицы поляризацией среды. Эта сила в
При дальнейшем увеличении энергии, когда параметр бмакс больше расстояний между атомами, рост потерь ограничивается из-за того, что действующая на далекий электрон сила уменьшена возникающей под действием поля частицы поляризацией среды. Эта сила в  раз меньше, чем в пустоте
раз меньше, чем в пустоте 
диэлектрическая проницаемость среды). На этом участке формула (68) уже несправедлива. С другой стороны, при далеких соударениях возникает новое физическое явление — так называемое излучение Вавилова-Черенкова, приводящее к дополнительным потерям энергии.
Из формулы (68) можно сделать основной вывод, что удельные потери энергии на ионизацию атомов:
пропорциональны квадрату заряда движущейся частицы  пропорциональны концентрации электронов в среде
пропорциональны концентрации электронов в среде  являются функцией скорости
являются функцией скорости  и не зависят от массы налетающей частицы
и не зависят от массы налетающей частицы  т. е.
т. е.

Так как величина удельных ионизационных потерь зависит от скорости и заряда частицы, то при одной и той же энергии удельные ионизационные потери для электрона будут во много раз меньше, чем для протона или  -частицы. Например, при энергиях порядка нескольких
-частицы. Например, при энергиях порядка нескольких  ионизационные потери электрона примерно в 10 000 раз меньше, чем у
ионизационные потери электрона примерно в 10 000 раз меньше, чем у  -частиц. Именно поэтому у
-частиц. Именно поэтому у  -частиц и электронов такая различная проникающая способность:
-частиц и электронов такая различная проникающая способность:  -частица в воздухе проходит всего лишь несколько сантиметров, прежде чем замедлится до тепловых скоростей, тогда как путь электрона такой же энергии измеряется десятками метров.
-частица в воздухе проходит всего лишь несколько сантиметров, прежде чем замедлится до тепловых скоростей, тогда как путь электрона такой же энергии измеряется десятками метров.
На наблюдении ионизации основан один из самых распространенных методов определения энергии медленных заряженных частиц. Определяется число пар ионов, создаваемых частицей на полном ее пути в веществе, и если известна средняя энергия необходимая для образования одной пары ионов, то можно найти полную энергию частицы. Для  -частицы, например, с энергией
-частицы, например, с энергией  в воздухе
в воздухе 
Простой вид зависимости от параметров частицы и среды позволяет легко пересчитывать ионизационные потери, если нужно перейти к другим частицам и средам. Например, если известны потери на ионизацию протона массы  как функция его энергии, то в области справедливости формулы (68) величина
как функция его энергии, то в области справедливости формулы (68) величина  может быть найдена при такой же энергии и для любой другой единично заряженной частицы с массой
может быть найдена при такой же энергии и для любой другой единично заряженной частицы с массой  путем умножения значения потерь энергии на величину отношения масс
путем умножения значения потерь энергии на величину отношения масс 
Действительно, согласно (66) потери энергии на ионизацию не зависят от массы частицы, но обратно пропорциональны квадрату ее скорости. Поэтому при равных энергиях они и будут пропорциональны значениям Масс.
В релятивистском случае потери энергии, как уже говорилось, пропорциональны логарифму квадрата скорости, поэтому при
одинаковых энергиях различие по массам в 2000 раз меняет ионизационную способность лишь в два раза.
Подобный пересчет может быть сделан и для падающих частиц с другим зарядом.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Масштабы физических величин.
- Особенности физических явлений в микромире.
- РАЗДЕЛ ПЕРВЫЙ. СТАБИЛЬНЫЕ ЯДРА И ЯДЕРНЫЕ СИЛЫ
- § 1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ПРОТОНА И НЕЙТРОНА
- § 2. ЗАРЯД АТОМНОГО ЯДРА
- § 3. РАЗМЕРЫ АТОМНЫХ ЯДЕР
- § 4. ЭНЕРГИЯ СВЯЗИ ЯДРА
- § 5. МАССА И ЭНЕРГИЯ
- § 6. СПИН И МАГНИТНЫЙ МОМЕНТ ЯДРА
- Методы определения спинов и магнитных моментов ядер.
- § 7. КВАДРУПОЛЬНЫЙ ЭЛЕКТРИЧЕСКИЙ МОМЕНТ ЯДРА
- § 8. ЧЕТНОСТЬ ВОЛНОВОЙ ФУНКЦИИ
- § 9. ЯДЕРНЫЕ МОДЕЛИ
- Глава вторая. ЯДЕРНЫЕ СИЛЫ
- § 10. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДЕРНЫХ СИЛ
- § 11. ФИЗИЧЕСКИЕ ОБОСНОВАНИЯ МЕЗОННОИ ТЕОРИИ ЯДЕРНЫХ СИЛ
- § 12. СТРУКТУРА НУКЛОНА
- § 13. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДЕЙТОНА
- Магнитный момент дейтона.
- РАЗДЕЛ ВТОРОЙ. НЕУСТОЙЧИВЫЕ ЯДРА
- § 14. ОТКРЫТИЕ РАДИОАКТИВНОСТИ
- § 15. ЗАКОНЫ РАДИОАКТИВНОГО РАСПАДА
- § 16. ТРАНСУРАНОВЫЕ ЭЛЕМЕНТЫ
- § 17. НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ ИЗОТОПОВ
- § 18. АЛЬФА-РАСПАД
- § 19. БЕТА-РАСПАД
- Энергетические спектры электронов при b-распаде и роль нейтрино.
- Энергетические соотношения при b-распаде.
- § 20. ГАММА-ИЗЛУЧЕНИЕ ЯДЕР
- Ядерная изомерия.
- Эффект Мёссбауера.
- ГЛАВА ЧЕТВЕРТАЯ. ВЗАИМОДЕЙСТВИЕ ЯДЕРНОГО ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
- § 21. ВИДЫ ВЗАИМОДЕЙСТВИЯ
- § 22. ВЗАИМОДЕЙСТВИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ СО СРЕДОЙ
- Пробег заряженных частиц в веществе.
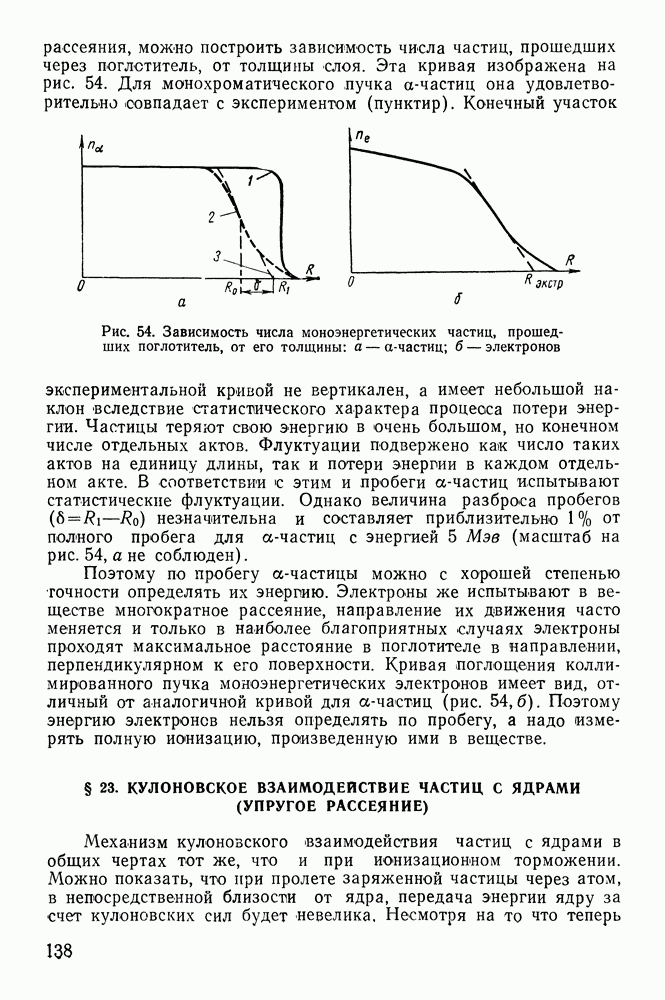
- § 23. КУЛОНОВСКОЕ ВЗАИМОДЕЙСТВИЕ ЧАСТИЦ С ЯДРАМИ (УПРУГОЕ РАССЕЯНИЕ)
- § 24. ЯДЕРНОЕ ВЗАИМОДЕЙСТВИЕ
- § 25. ИЗЛУЧЕНИЕ ВАВИЛОВА — ЧЕРЕНКОВА
- § 26. ПРОХОЖДЕНИЕ ГАММА-ИЗЛУЧЕНИЯ ЧЕРЕЗ ВЕЩЕСТВО
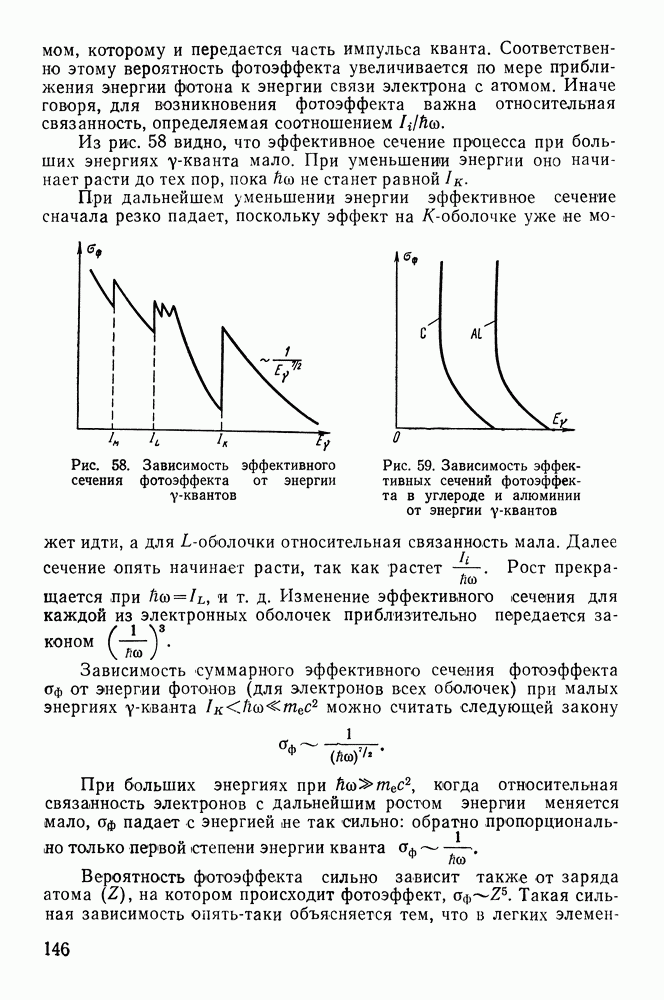
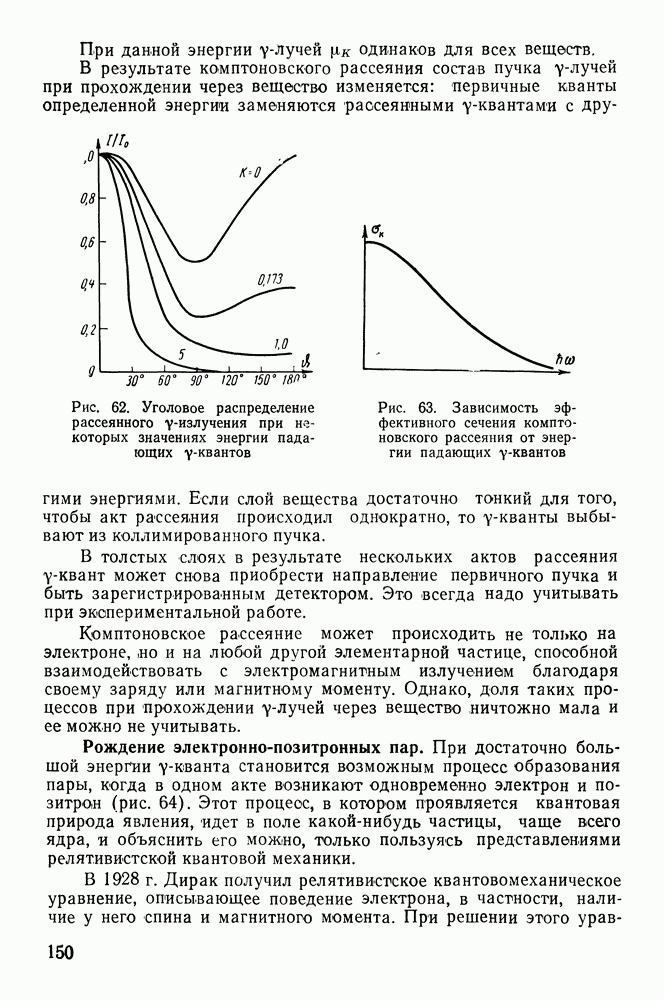
- Рассеяние y-лучей. Эффект Комптона.
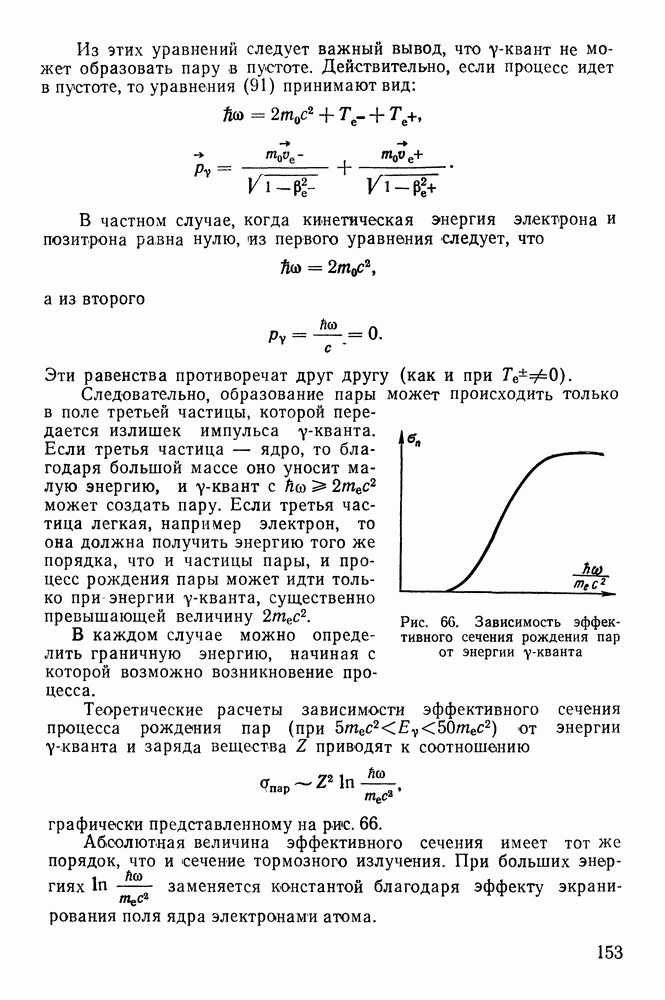
- Рождение электронно-позитронных пар.
- Другие эффекты, возникающие при поглощении y-лучей
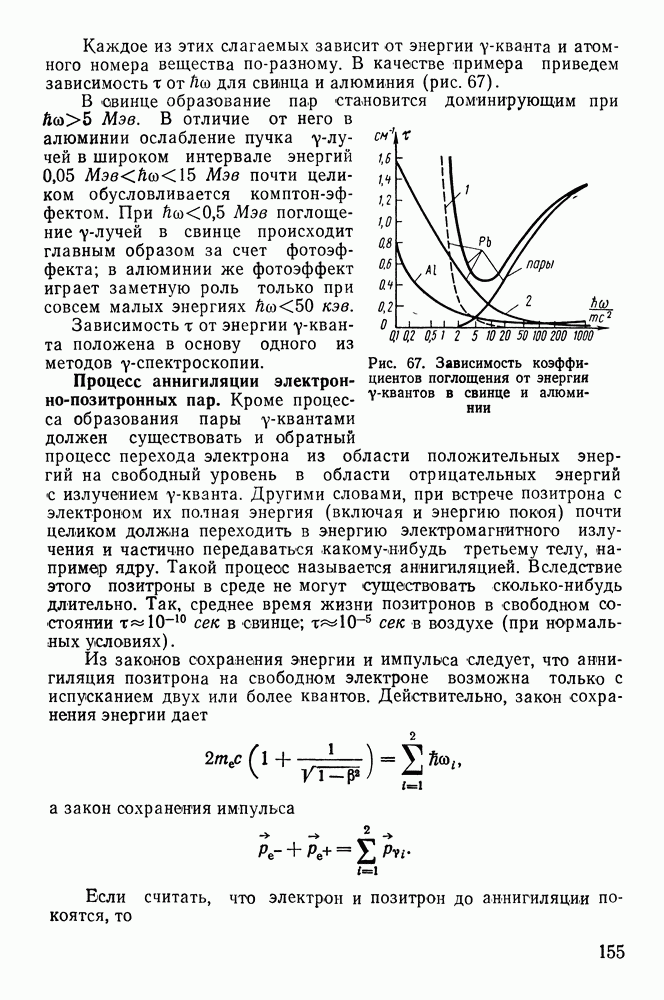
- Суммарный коэффициент поглощения y-излучения
- Процесс аннигиляции электронно-позитронных пар.
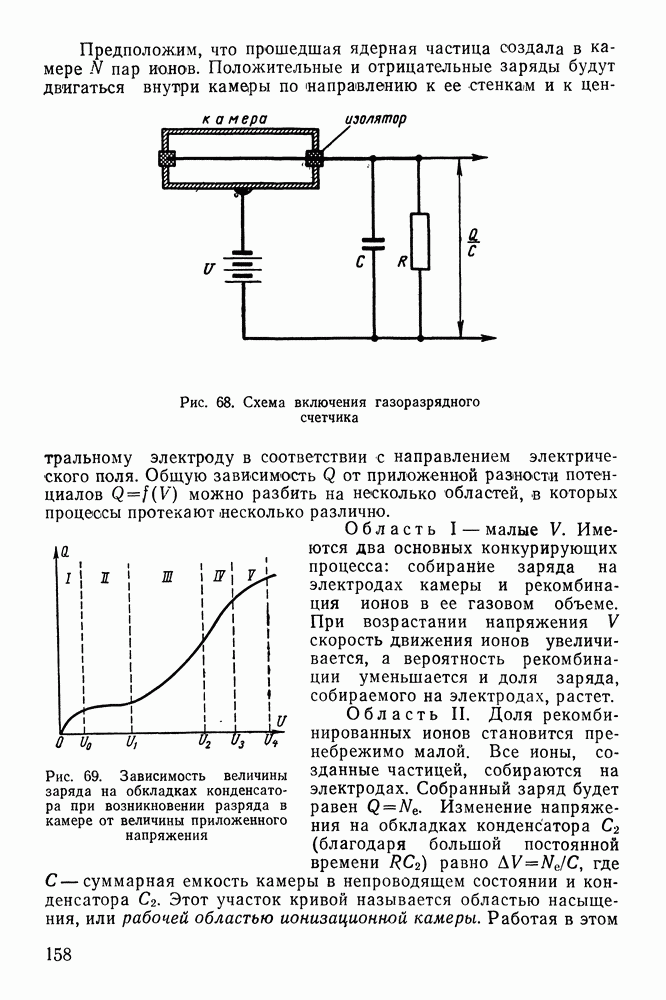
- § 27. МЕТОДЫ РЕГИСТРАЦИИ ИЗЛУЧЕНИЯ
- РАЗДЕЛ ТРЕТИЙ. ЯДЕРНЫЕ РЕАКЦИИ
- ГЛАВА ПЯТАЯ. ЗАКОНОМЕРНОСТИ ЯДЕРНЫХ РЕАКЦИЙ
- § 29. ЗАКОНЫ СОХРАНЕНИЯ В ЯДЕРНЫХ РЕАКЦИЯХ
- § 30. РАЗЛИЧНЫЕ МЕХАНИЗМЫ РЕАКЦИЙ
- ГЛАВА ШЕСТАЯ. ФИЗИКА НЕЙТРОНОВ
- § 31. ОТКРЫТИЕ НЕЙТРОНА И ЕГО СВОЙСТВА
- § 32. ИСТОЧНИКИ НЕЙТРОНОВ
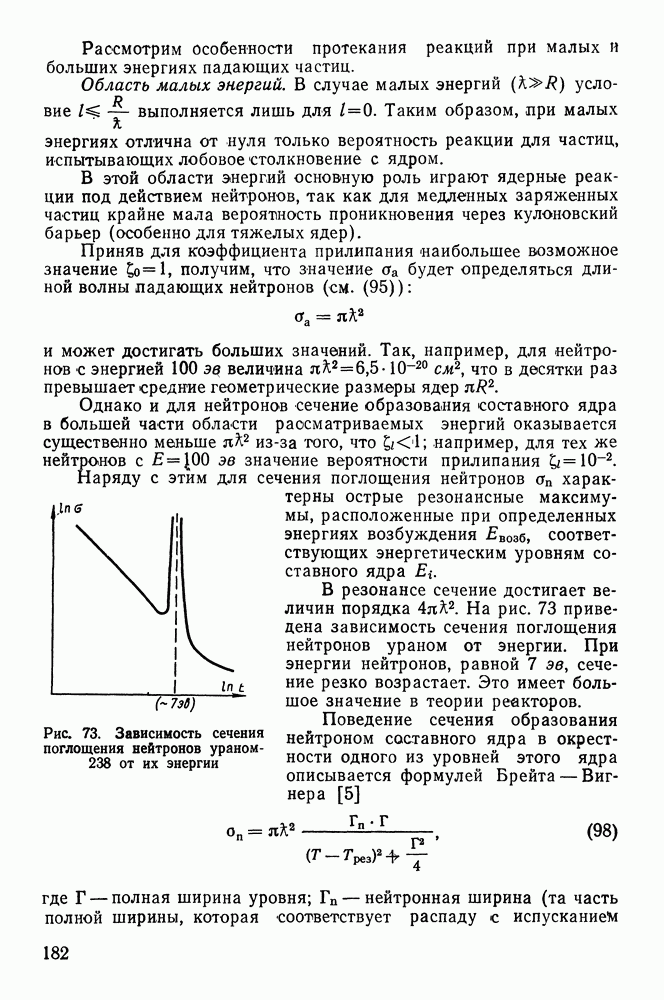
- § 33. ВЗАИМОДЕЙСТВИЕ НЕЙТРОНОВ С ВЕЩЕСТВОМ
- § 34. МЕТОДЫ РЕГИСТРАЦИИ НЕЙТРОНОВ
- § 35. ЗАМЕДЛЕНИЕ НЕЙТРОНОВ
- § 36. МЕТОДЫ ПОЛУЧЕНИЯ МОНОХРОМАТИЧЕСКИХ НЕЙТРОНОВ
- ГЛАВА СЕДЬМАЯ. ДЕЛЕНИЕ И СИНТЕЗ ЯДЕР
- § 37. ОТКРЫТИЕ ДЕЛЕНИЯ ЯДЕР
- § 38. ПРОЦЕССЫ, ПРОИСХОДЯЩИЕ ПРИ ДЕЛЕНИИ ЯДЕР УРАНА
- § 39. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДЕЛЕНИЯ
- § 40. ТИПЫ РЕАКЦИЙ ДЕЛЕНИЯ
- § 41. ВОЗМОЖНОСТЬ ИСПОЛЬЗОВАНИЯ ЯДЕРНОЙ ЭНЕРГИИ
- § 42. ЦЕПНАЯ ЯДЕРНАЯ РЕАКЦИЯ И ЯДЕРНЫЕ РЕАКТОРЫ
- § 43. ТЕРМОЯДЕРНЫЙ СИНТЕЗ
- Термоядерные реакции в лабораторных условиях.
- РАЗДЕЛ ЧЕТВЕРТЫЙ. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ И КОСМИЧЕСКИЕ ЛУЧИ
- § 44. ОТКРЫТИЕ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
- § 45. ВИДЫ ВЗАИМОДЕЙСТВИЯ ЧАСТИЦ
- § 46. КЛАССИФИКАЦИЯ ЧАСТИЦ
- § 47. РЕАКЦИИ МЕЖДУ ЧАСТИЦАМИ
- § 48. ВНУТРЕННИЕ СВОЙСТВА ЧАСТИЦ
- § 49. РЕЗОНАНСЫ
- § 50. ПОПЫТКИ СИСТЕМАТИЗАЦИИ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
- § 51. ГИПЕРФРАГМЕНТЫ (ИЛИ Л°-ЯДРА)
- § 52. НАРУШЕНИЕ ЗАКОНА СОХРАНЕНИЯ ЧЕТНОСТИ
- § 53. ФИЗИКА НЕЙТРИНО
- ГЛАВА ДЕВЯТАЯ. КОСМИЧЕСКИЕ ЛУЧИ
- § 54. ОТКРЫТИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- § 55. ПЕРВИЧНОЕ ИЗЛУЧЕНИЕ У ЗЕМЛИ
- § 56. ВЗАИМОДЕЙСТВИЕ КОСМИЧЕСКОГО ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
- § 57. СОСТАВ КОСМИЧЕСКИХ ЛУЧЕЙ НА УРОВНЕ МОРЯ
- § 58. ВРЕМЕННЫЕ ИЗМЕНЕНИЯ ИНТЕНСИВНОСТИ КОСМИЧЕСКИХ ЛУЧЕЙ
- § 59. РАДИАЦИОННЫЕ ПОЯСА
- § 60. ПРОИСХОЖДЕНИЕ КОСМИЧЕСКИХ ЛУЧЕЙ
- ЗАКЛЮЧЕНИЕ
- ЛИТЕРАТУРА