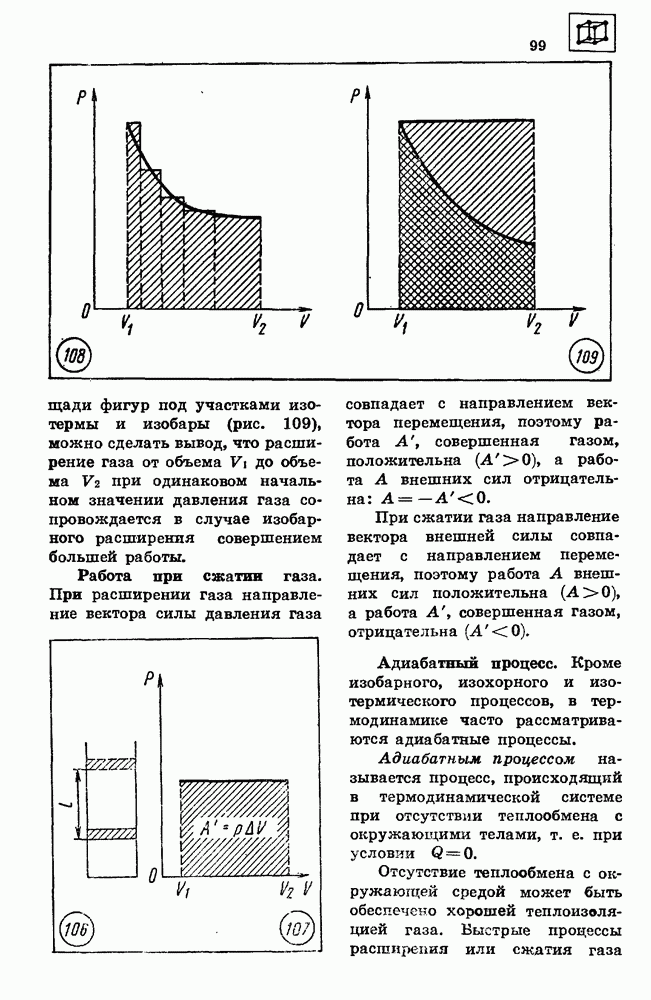
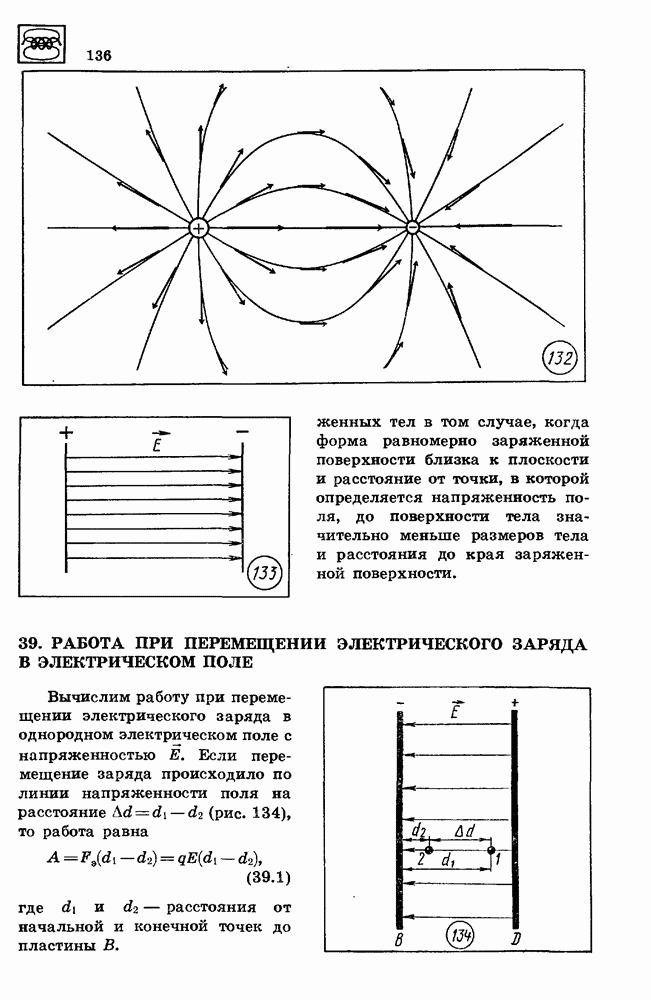
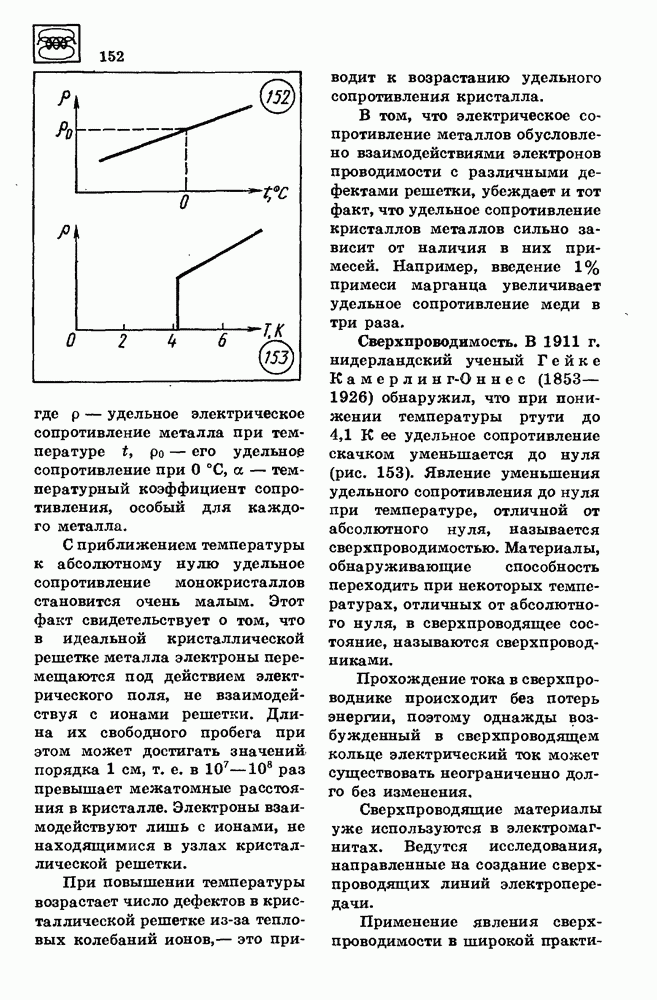
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
Движение любого тела в реальных условиях никогда не бывает строго равномерным и прямолинейным. Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным движением.
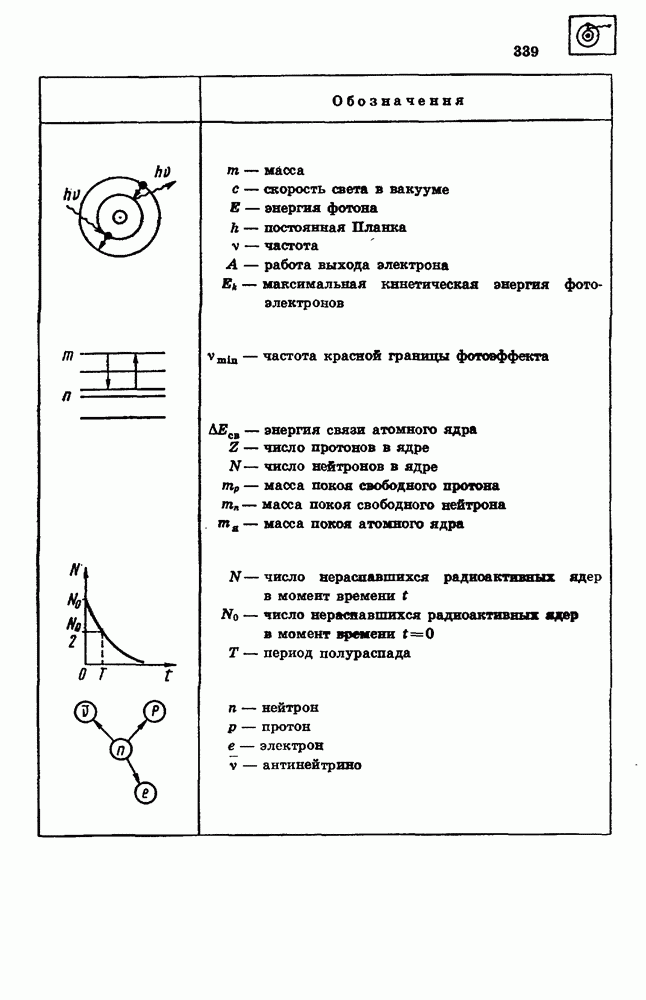
Ускорение.
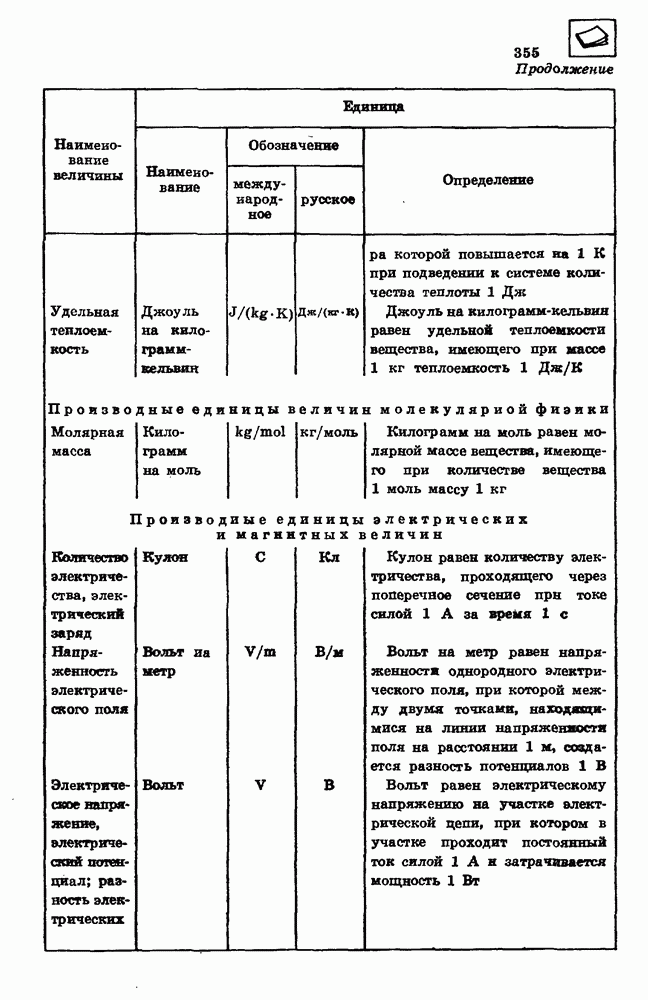
При неравномерном поступательном движении скорость тела изменяется с течением времени. Процесс изменения скорости тела характеризуется ускорением. Ускорением называется векторная величина, равная отношению очень малого изменения вектора скорости  к малому промежутку времени
к малому промежутку времени  за которое произошло это изменение:
за которое произошло это изменение:

Если за промежуток времени  тело из точки А траектории переместилось в точку В и его скорость изменилась от
тело из точки А траектории переместилось в точку В и его скорость изменилась от  до
до  , то изменение скорости
, то изменение скорости  за этот промежуток времени равно разности векторов
за этот промежуток времени равно разности векторов 

Направление вектора ускорения а совпадает с направлением вектора изменения скорости А и при очень малых значениях промежутка времени  за который происходит изменение скорости.
за который происходит изменение скорости.
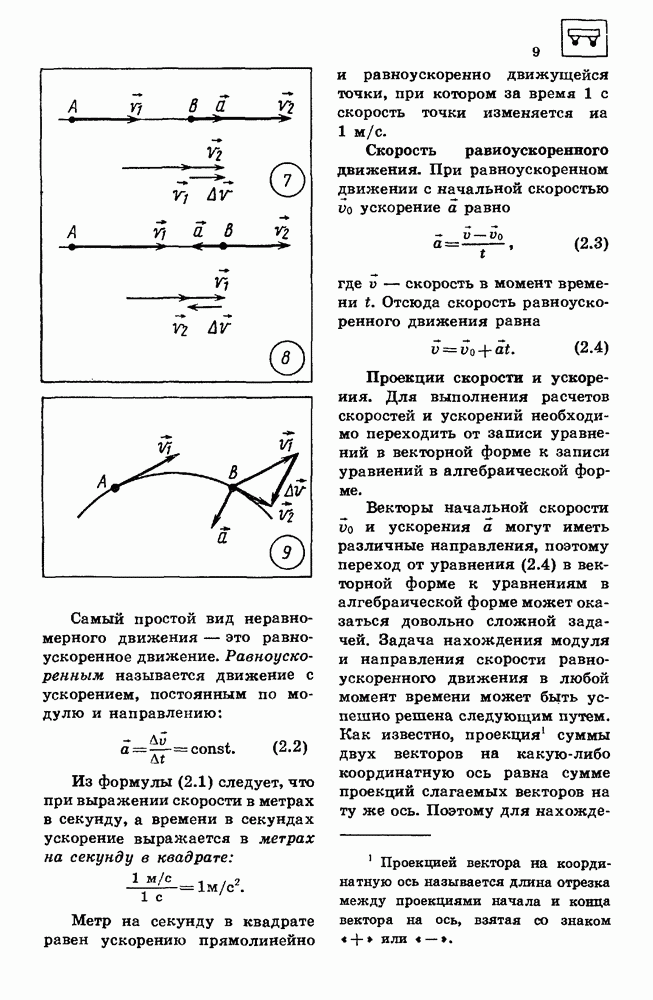
Если тело движется прямолинейно и скорость его возрастает по модулю, т. е. то направление вектора ускорения совпадает с направлением вектора скорости  (рис. 7); при убывании скорости по модулю, т. е. при
(рис. 7); при убывании скорости по модулю, т. е. при  направление вектора ускорения противоположно направлению вектора скорости
направление вектора ускорения противоположно направлению вектора скорости  (рис. 8).
(рис. 8).
При движении тела по криволинейной траектории направление вектора скорости изменяется в процессе движения, вектор ускорения а при этом может оказаться направлен под любым углом к вектору скорости  (рис. 9).
(рис. 9).



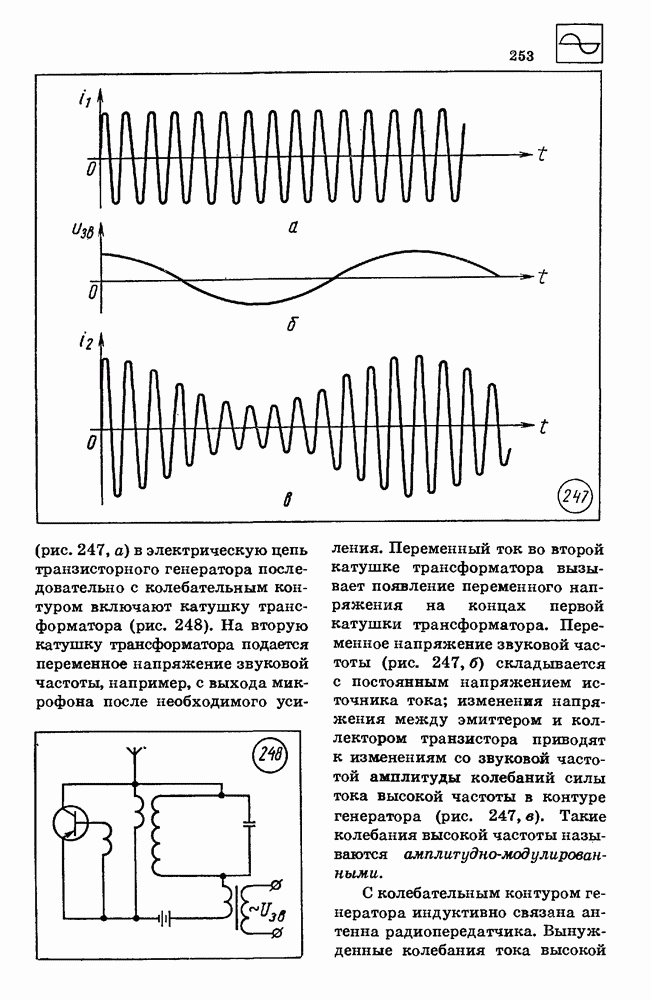
Самый простой вид неравномерного движения — это равноускоренное движение. Равноускоренным называется движение с ускорением, постоянным по модулю и направлению:

Из формулы (2.1) следует, что при выражении скорости в метрах в секунду, а времени в секундах ускорение выражается в метрах на секунду в квадрате:

Метр на секунду в квадрате равен ускорению прямолинейно и равноускоренно движущейся точки, при котором за время 1 с скорость точки изменяется на 1 м/с.
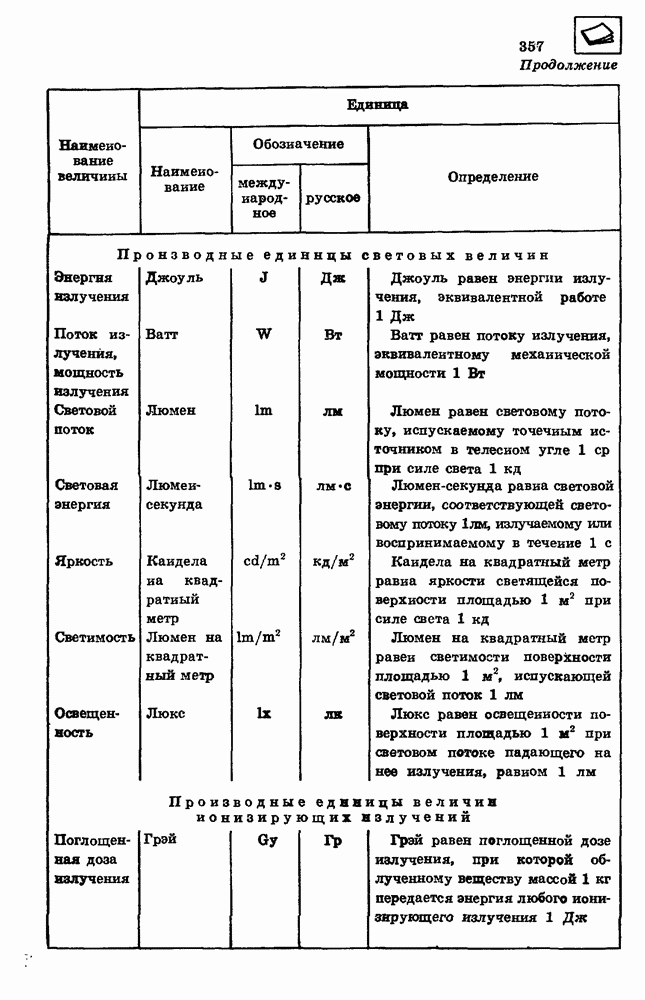
Скорость равноускоренного движения.
При равноускоренном движении с начальной скоростью  ускорение а равно
ускорение а равно

где  — скорость в момент времени
— скорость в момент времени  Отсюда скорость равноускоренного движения равна
Отсюда скорость равноускоренного движения равна

Проекции скорости и ускорения.
Для выполнения расчетов скоростей и ускорений необходимо переходить от записи уравнений в векторной форме к записи уравнений в алгебраической форме.
Векторы начальной скорости до и ускорения а могут иметь различные направления, поэтому переход от уравнения (2.4) в векторной форме к уравнениям в алгебраической форме может оказаться довольно сложной задачей. Задача нахождения модуля и направления скорости равноускоренного движения в любой момент времени может быть успешно решена следующим путем. Как известно, проекция суммы двух векторов на какую-либо координатную ось равна сумме проекций слагаемых векторов на ту же ось. Поэтому для нахождения
проекции  вектора скорости
вектора скорости  на произвольную ось
на произвольную ось  нужно найти алгебраическую сумму проекций векторов
нужно найти алгебраическую сумму проекций векторов  на ту же ось:
на ту же ось:

Проекцию вектора на ось считают положительной, если от проекции начала к проекции конца вектора нужно идти по направлению оси, и отрицательной — в противоположном случае.
Так, в случае расположения векторов  представленном на рисунке 10, их проекции
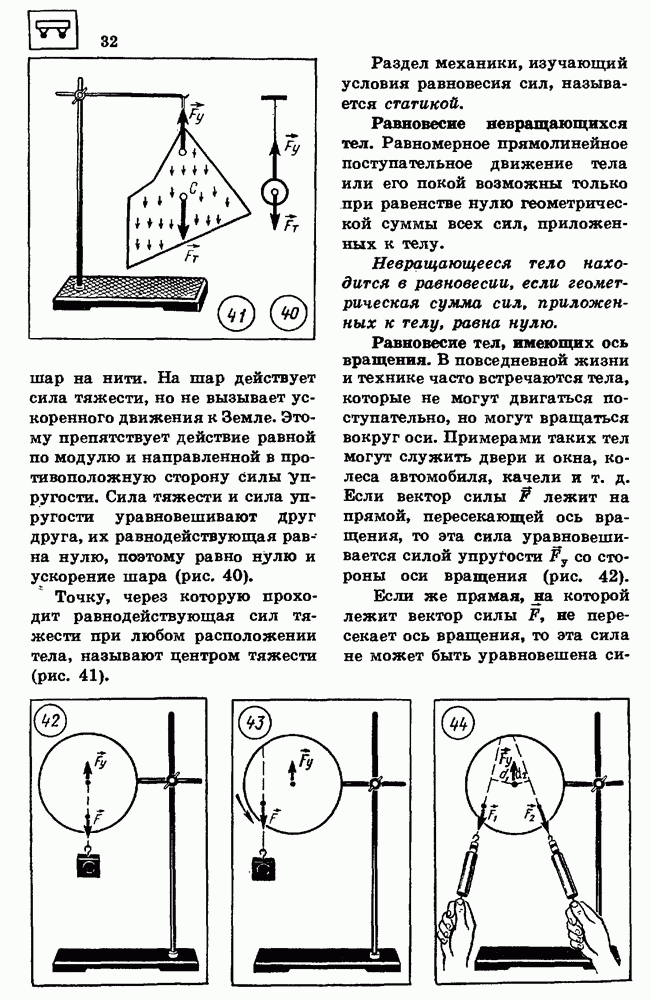
представленном на рисунке 10, их проекции  на ось
на ось  положительны. В случае расположения векторов
положительны. В случае расположения векторов  представленном на рисунке 11, проекция
представленном на рисунке 11, проекция  положительна, а проекция
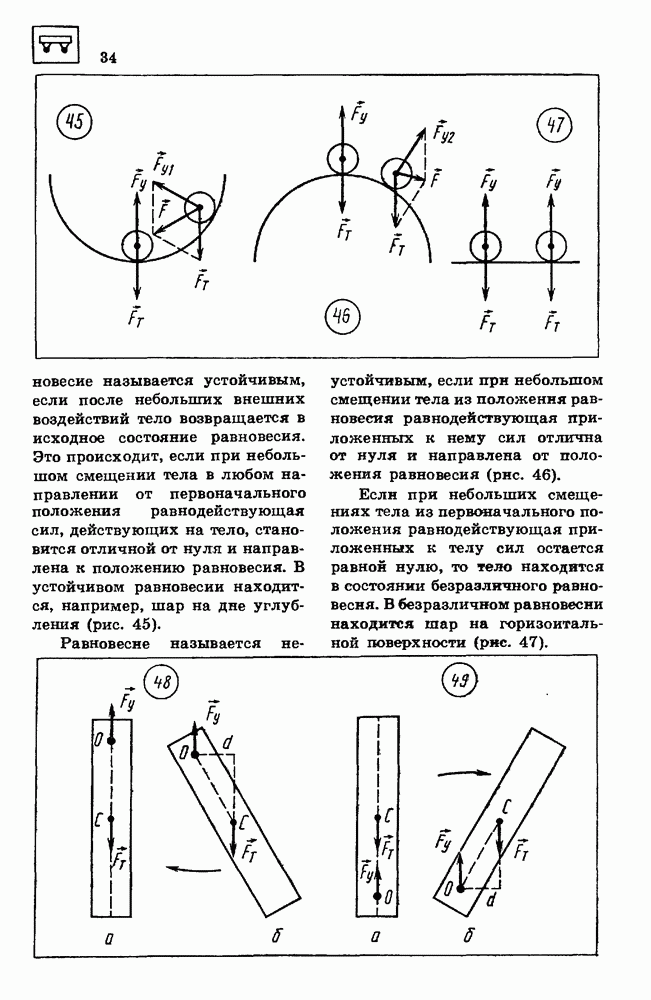
положительна, а проекция  отрицательна.
отрицательна.
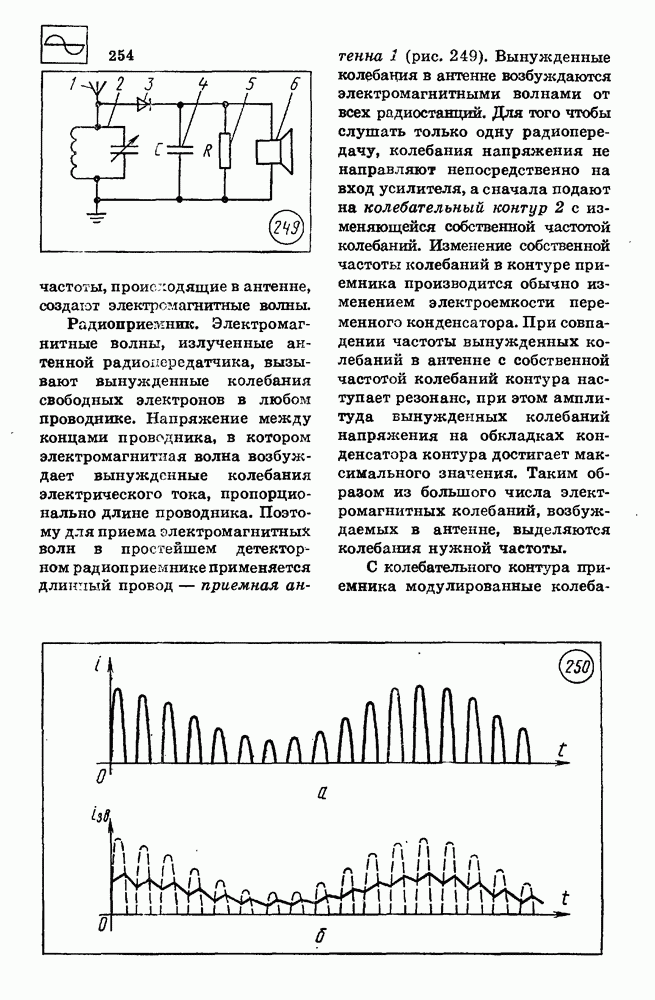
График скорости.
Из уравнения (2.5) следует, что графиком зависимости проекции скорости равноускоренного движения от времени является прямая. Если проекция начальной скорости на ось  равна нулю
равна нулю  то эта прямая проходит через начало координат (рис. 12).
то эта прямая проходит через начало координат (рис. 12).




Графики зависимости проекции скорости  от времени
от времени  для равноускоренных движений, происходящих с одинаковой начальной скоростью
для равноускоренных движений, происходящих с одинаковой начальной скоростью  и различным ускорением а, приведены на рисунке 13.
и различным ускорением а, приведены на рисунке 13.
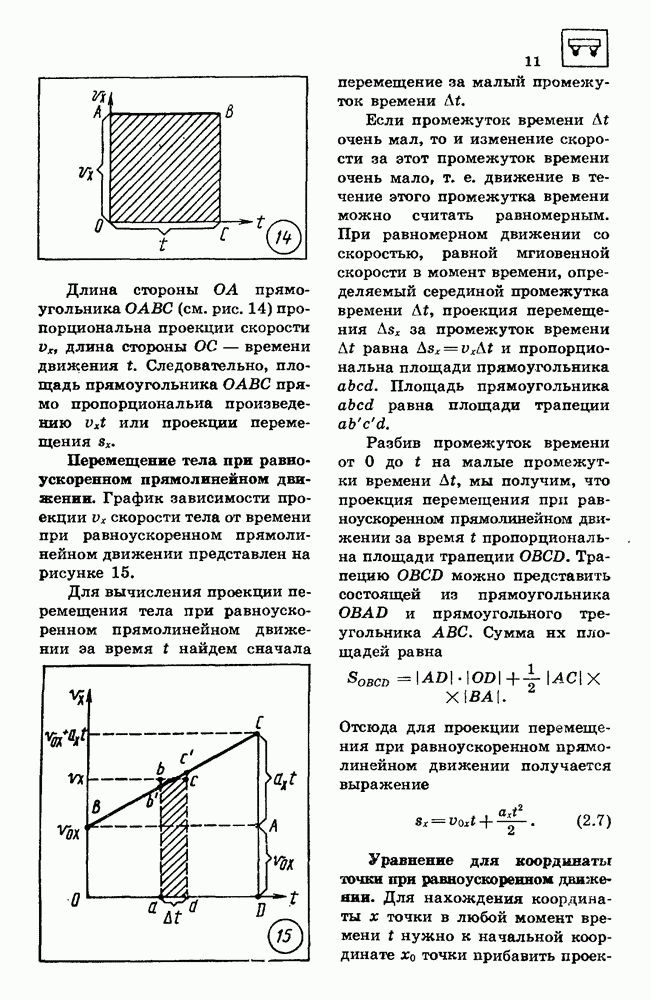
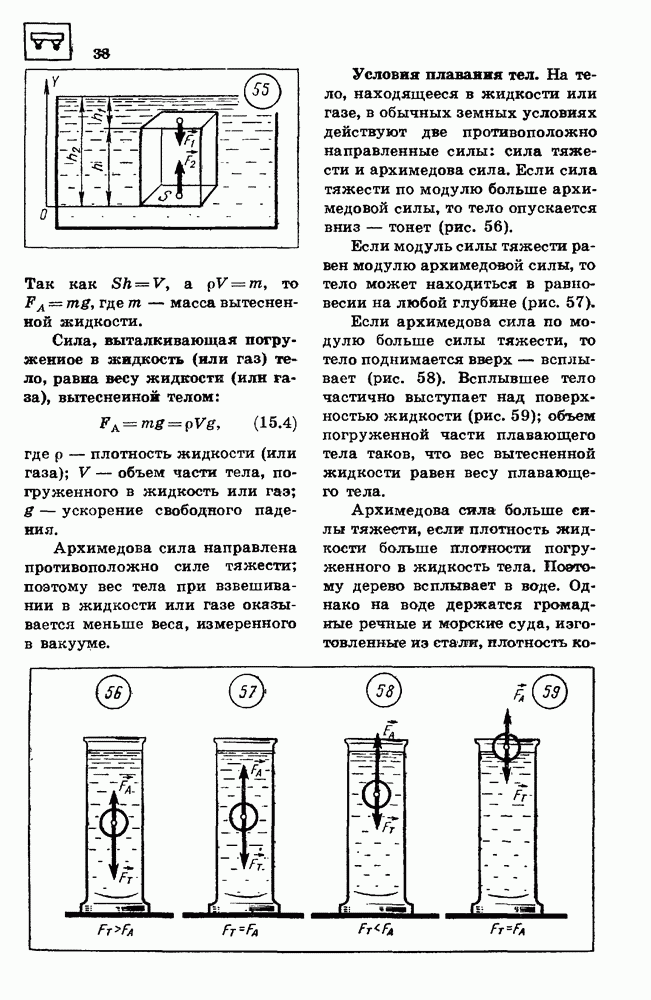
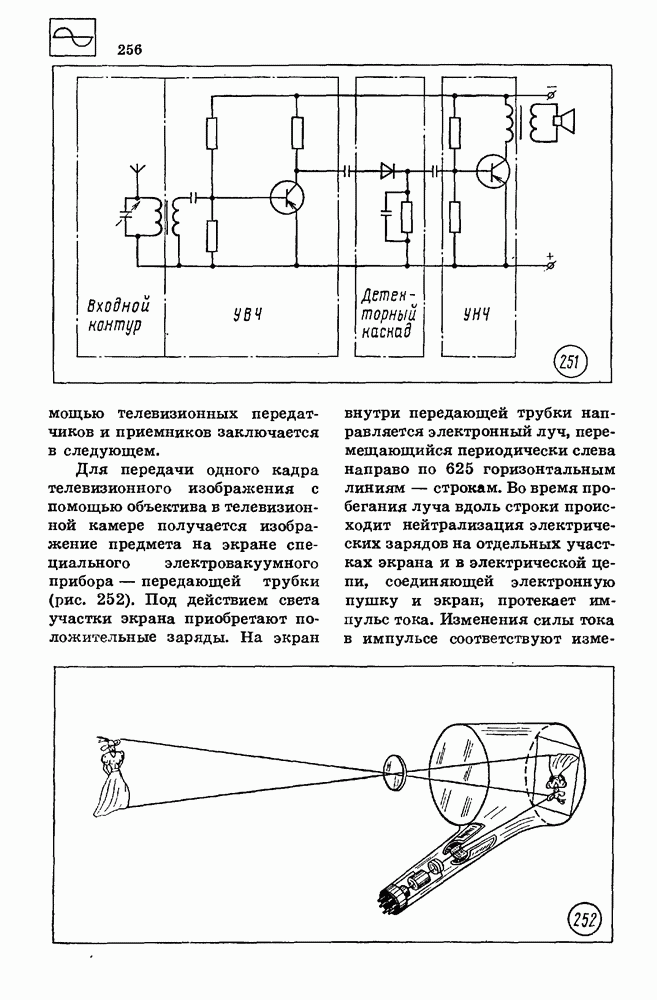
Перемещение тела при равно мерном движении.
Установим связь проекции  вектора перемещения на координатную ось
вектора перемещения на координатную ось  при равномерном прямолинейном движении с проекцией
при равномерном прямолинейном движении с проекцией  вектора скорости на ту же ось и временем
вектора скорости на ту же ось и временем 
При равномерном прямолинейном движении график зависимости проекции скорости  от времени
от времени  является прямой, параллельной оси абсцисс (рис. 14).
является прямой, параллельной оси абсцисс (рис. 14).
Проекция 8 перемещения тела за время  при равномерном движении со скоростью
при равномерном движении со скоростью  (см. формулу 1.1) определяется выражением
(см. формулу 1.1) определяется выражением


Длина стороны  прямоугольника
прямоугольника  (см. рис. 14) пропорциональна проекции скорости
(см. рис. 14) пропорциональна проекции скорости  длина стороны
длина стороны  — времени движения
— времени движения  Следовательно, площадь прямоугольника
Следовательно, площадь прямоугольника  прямо пропорциональна произведению
прямо пропорциональна произведению  или проекции перемещения
или проекции перемещения 
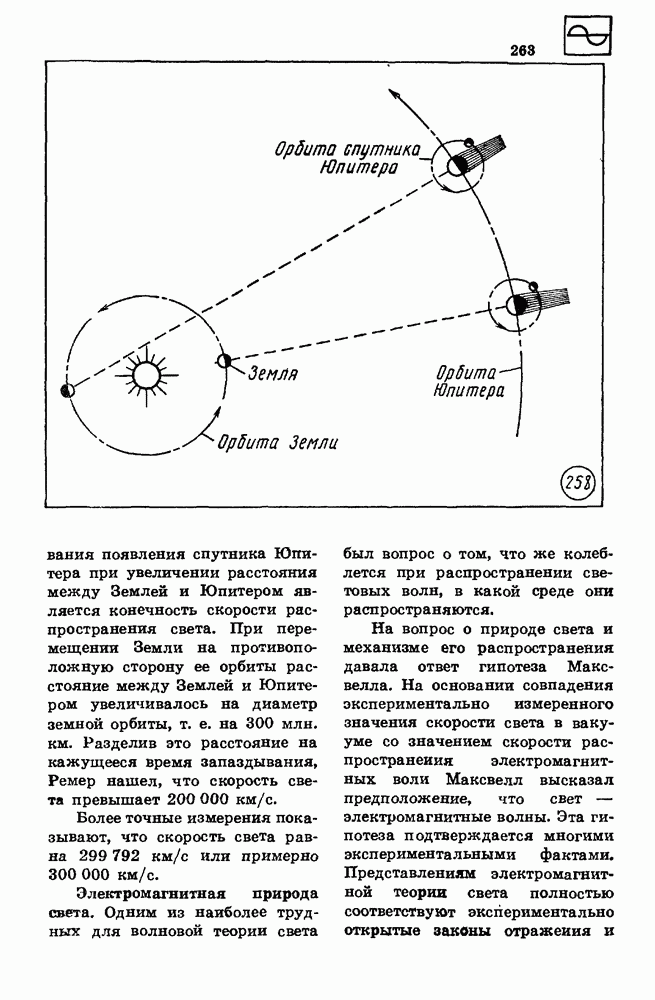
Перемещение тела при равноускоренном прямолинейном движении.
График зависимости проекции  скорости тела от времени при равноускоренном прямолинейном движении представлен на рисунке 15.
скорости тела от времени при равноускоренном прямолинейном движении представлен на рисунке 15.
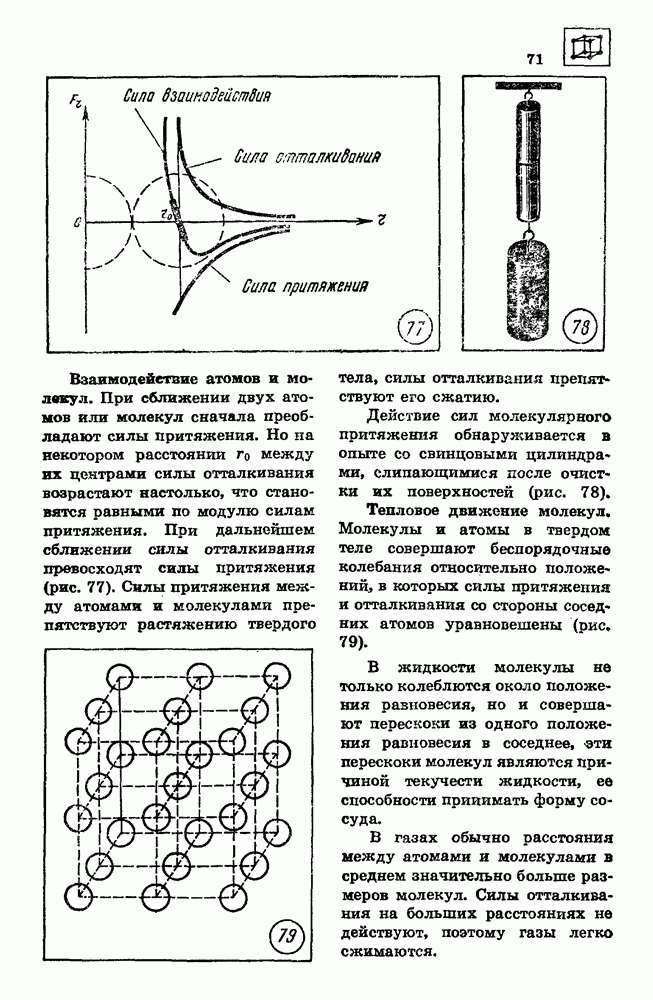
Для вычисления проекции перемещения тела при равноускоренном прямолинейном движении  время
время  найдем сначала перемещение за малый промежуток времени
найдем сначала перемещение за малый промежуток времени 

Если промежуток времени  очень мал, то и изменение скорости за этот промежуток времени очень мало, т. е. движение в течение этого промежутка времени можно считать равномерным. При равномерном движении со скоростью, равной мгновенной скорости в момент времени, определяемый серединой промежутка времени
очень мал, то и изменение скорости за этот промежуток времени очень мало, т. е. движение в течение этого промежутка времени можно считать равномерным. При равномерном движении со скоростью, равной мгновенной скорости в момент времени, определяемый серединой промежутка времени  проекция перемещения
проекция перемещения  за промежуток времени
за промежуток времени  равна
равна  и пропорциональна площади прямоугольника
и пропорциональна площади прямоугольника  Площадь прямоугольника
Площадь прямоугольника  равна площади трапеции
равна площади трапеции 
Разбив промежуток времени от 0 до  на малые промежутки времени
на малые промежутки времени  мы получим, что проекция перемещения при равноускоренном прямолинейном движении за время
мы получим, что проекция перемещения при равноускоренном прямолинейном движении за время  пропорциональна площади трапеции
пропорциональна площади трапеции  Трапецию
Трапецию  можно представить состоящей из прямоугольника
можно представить состоящей из прямоугольника  и прямоугольного треугольника
и прямоугольного треугольника  Сумма
Сумма  площадей равна
площадей равна

Отсюда для проекции перемещения при равноускоренном прямолинейном движении получается выражение

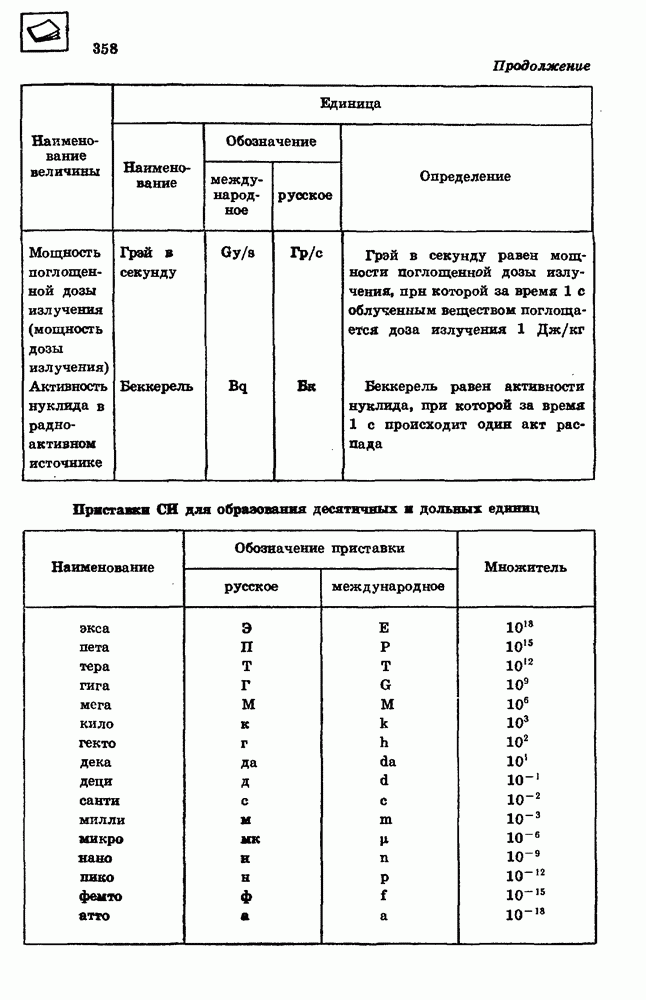
Уравнение для координаты точки при равноускоренном движении.
Для нахождения координаты х точки в любой момент времени  нужно к начальной координате
нужно к начальной координате  точки прибавить проекцию
точки прибавить проекцию

вектора перемещения на ось  (рис. 16):
(рис. 16):

Из выражений (2.8) и (2.7) следует: 2

Связь проекции перемещения тела с конечной скоростью при равноускоренном движении.
Из уравнений (2.5) и (2.7) можно получить уравнение, связывающее проекции конечной скорости  начальной скорости
начальной скорости  и ускорения
и ускорения  с проекцией перемещения тела
с проекцией перемещения тела 

В случае равенства проекции начальной скорости нулю получаем выражение

Из этого выражения можно найти проекции скорости  или ускорения
или ускорения  по известному значению проекции перемещения
по известному значению проекции перемещения 

| << Предыдущий параграф | Следующий параграф >> |
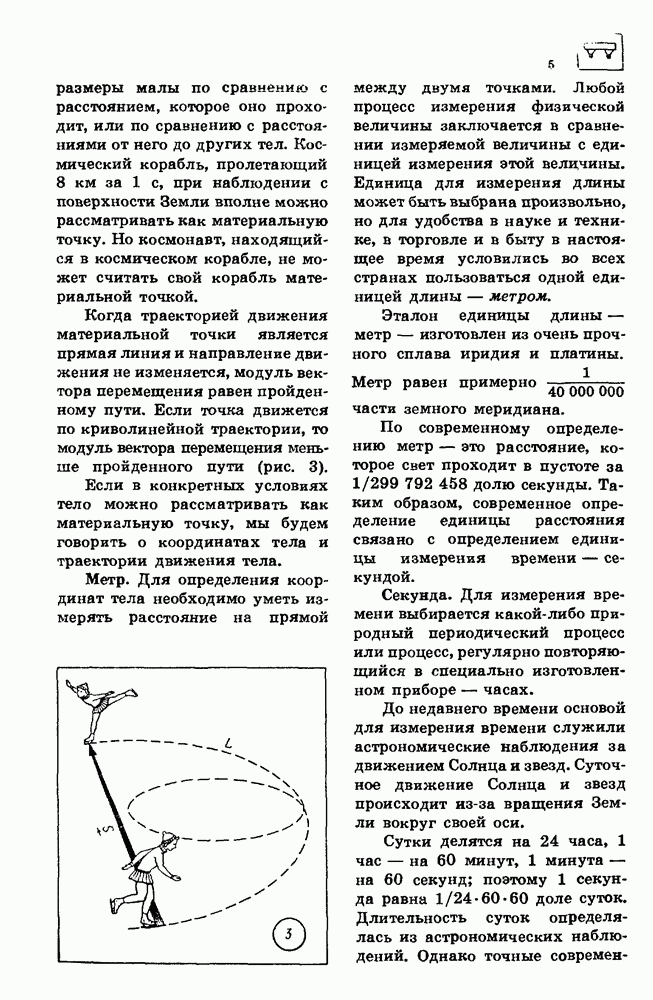
- 1. МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ
- 2. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- 3. РАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
- 4. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- 5. МАССА ТЕЛА
- 6. СИЛА
- 7. ВТОРОЙ ЗАКОН НЬЮТОНА
- 8. ТРЕТИЙ ЗАКОН НЬЮТОНА
- 9. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
- 10. ВЕС И НЕВЕСОМОСТЬ
- 11. ДВИЖЕНИЕ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- 12. СИЛА УПРУГОСТИ
- 13. СИЛЫ ТРЕНИЯ
- 14. УСЛОВИЯ РАВНОВЕСИЯ ТЕЛ
- 15. ЭЛЕМЕНТЫ ГИДРОСТАТИКИ
- 16. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- 17. РЕАКТИВНОЕ ДВИЖЕНИЕ
- 18. МЕХАНИЧЕСКАЯ РАБОТА
- 19. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- 20. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
- 21. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ В МЕХАНИЧЕСКИХ ПРОЦЕССАХ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 22. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОИ ТЕОРИИ И ИХ ОПЫТНОЕ ОБОСНОВАНИЕ
- 23. МАССА МОЛЕКУЛ
- 24. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОИ ТЕОРИИ ИДЕАЛЬНОГО ГАЗА
- 25. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- 28. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- 27. СВОЙСТВА ЖИДКОСТЕЙ
- 28. ИСПАРЕНИЕ И КОНДЕНСАЦИЯ
- 29. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА
- 30. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ЦЕЛ
- 31. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 32. КОЛИЧЕСТВО ТЕПЛОТЫ
- 33. РАБОТА ПРИ ИЗМЕНЕНИИ ОБЪЕМА ГАЗА
- 34. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДБИГАТЕЛЕЙ
- 35. ТЕПЛОВЫЕ МАШИНЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 36. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- 37. ЗАКОН КУЛОНА
- 38. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 39. РАБОТА ПРИ ПЕРЕМЕЩЕНИИ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- 40. ПОТЕНЦИАЛ
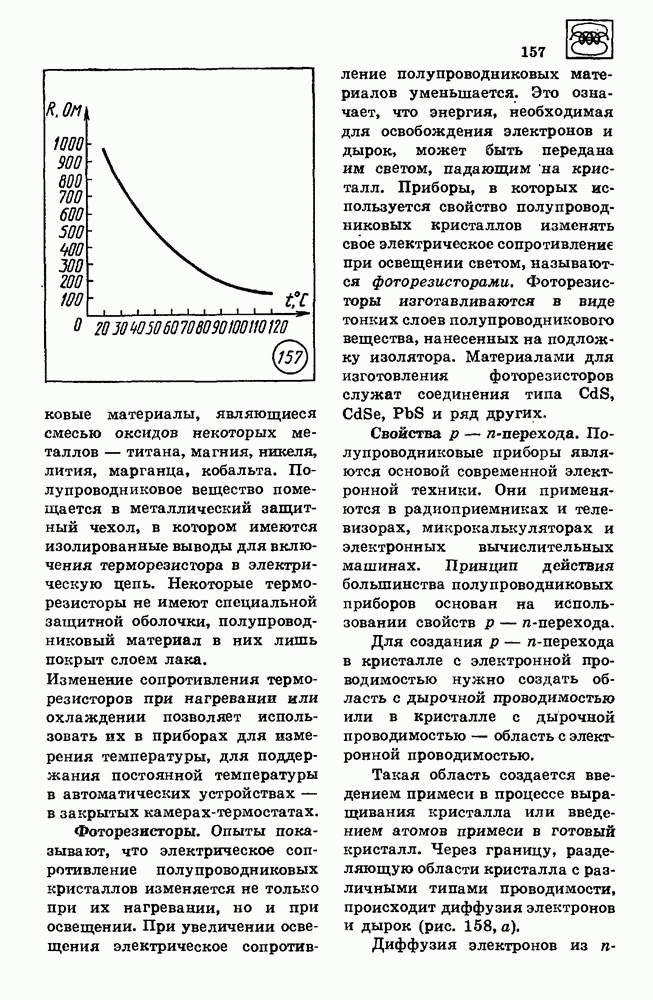
- 41. ВЕЩЕСТВО В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- 42. ЭЛЕКТРОЕМКОСТЬ
- 43. ЗАКОН ОМА
- 44. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ
- 45. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- 46. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ
- 47. ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
- 48. ОТКРЫТИЕ ЭЛЕКТРОНА
- 49. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ
- 50. ЭЛЕКТРИЧЕСКИИ ТОК В ВАКУУМЕ
- 51. МАГНИТНОЕ ПОЛЕ
- 52. СИЛА ЛОРЕНЦА
- 53. ВЕЩЕСТВО В МАГНИТНОМ ПОЛЕ
- 54. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
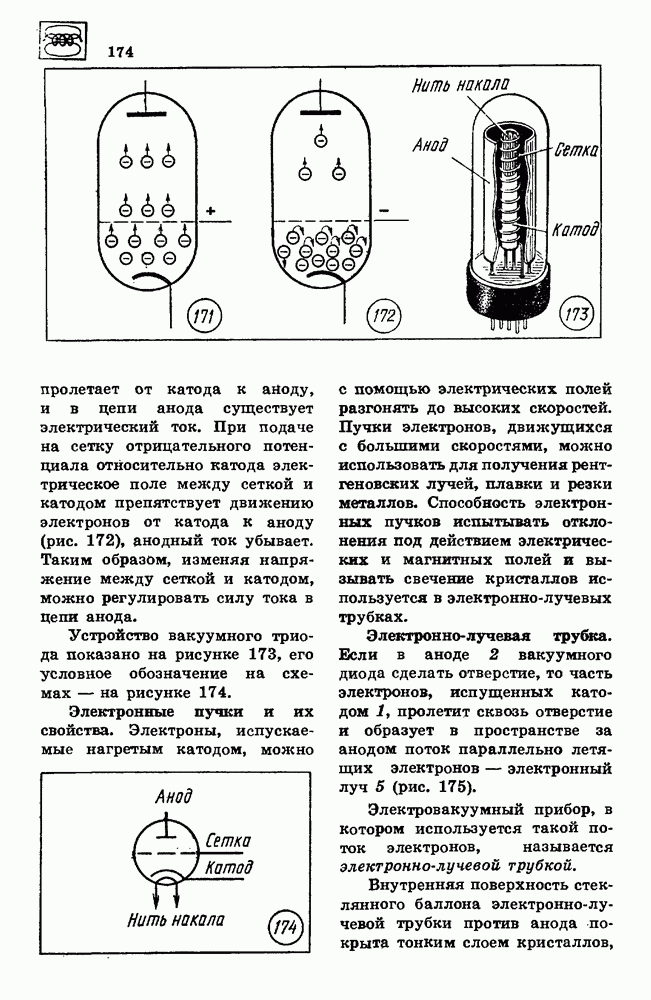
- 55. САМОИНДУКЦИЯ
- 56. МАГНИТНАЯ ЗАПИСЬ ИНФОРМАЦИИ
- 57. МАШИНА ПОСТОЯННОГО ТОКА
- 58. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
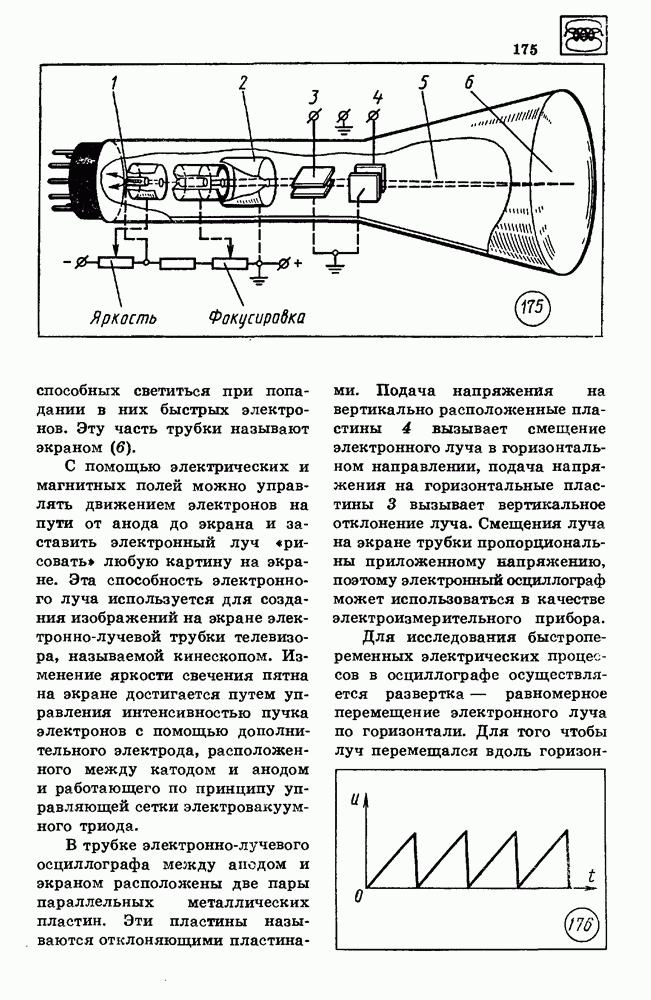
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 59. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
- 60. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
- 61. ПРЕВРАЩЕНИЯ ЭНЕРГИИ ПРИ МЕХАНИЧЕСКИХ КОЛЕБАНИЯХ
- 62. РАСПРОСТРАНЕНИЕ КОЛЕБАНИИ В УПРУГОЙ СРЕДЕ
- 63. ЗВУКОВЫЕ ВОЛНЫ
- 64. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ВОЛН
- 65. ИНТЕРФЕРЕНЦИЯ, ДИФРАКЦИЯ И ПОЛЯРИЗАЦИЯ ВОЛН
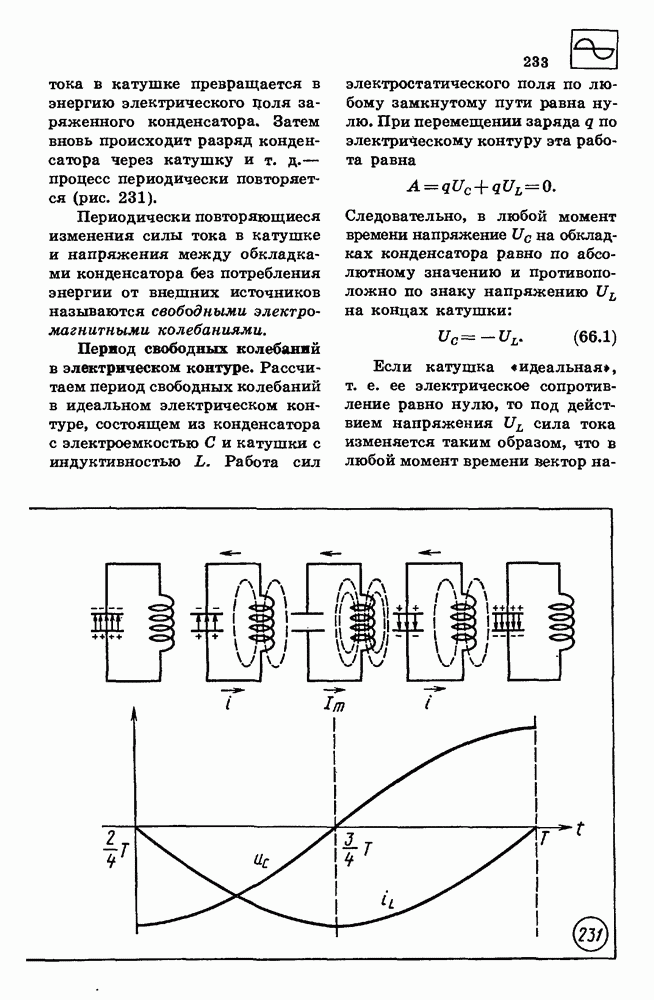
- 66. СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
- 67. АВТОКОЛЕБАТЕЛЬНЫЙ ГЕНЕРАТОР НЕЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИИ
- 68. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- 69. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 70. ИНДУКТИВНОСТЬ И ЕМКОСТЬ В ЦКТТИ ПЕРЕМЕННОГО ТОКА
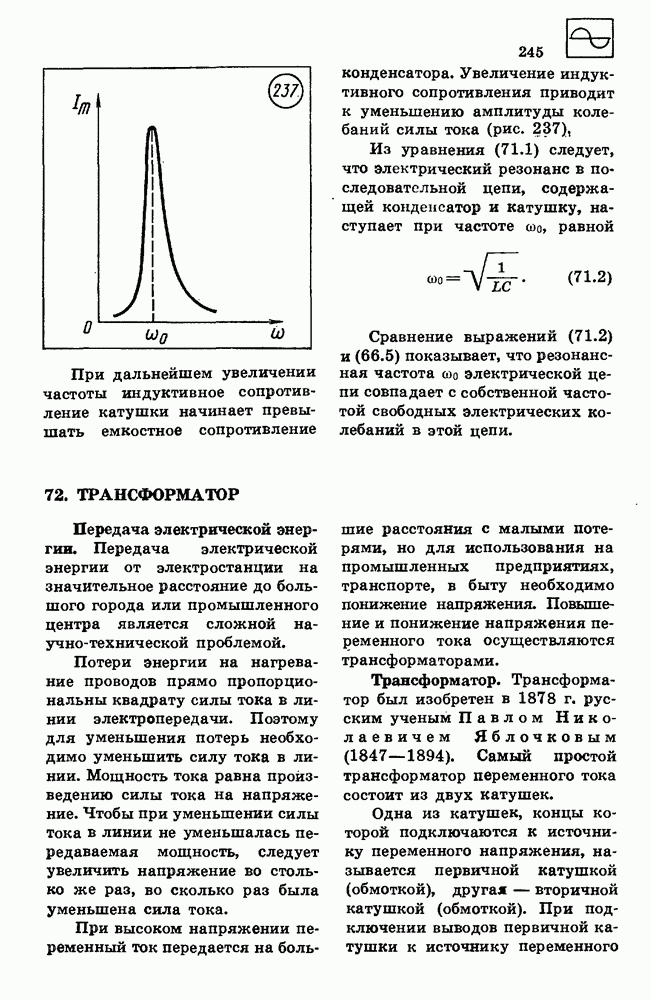
- 71. РЕЗОНАНС В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
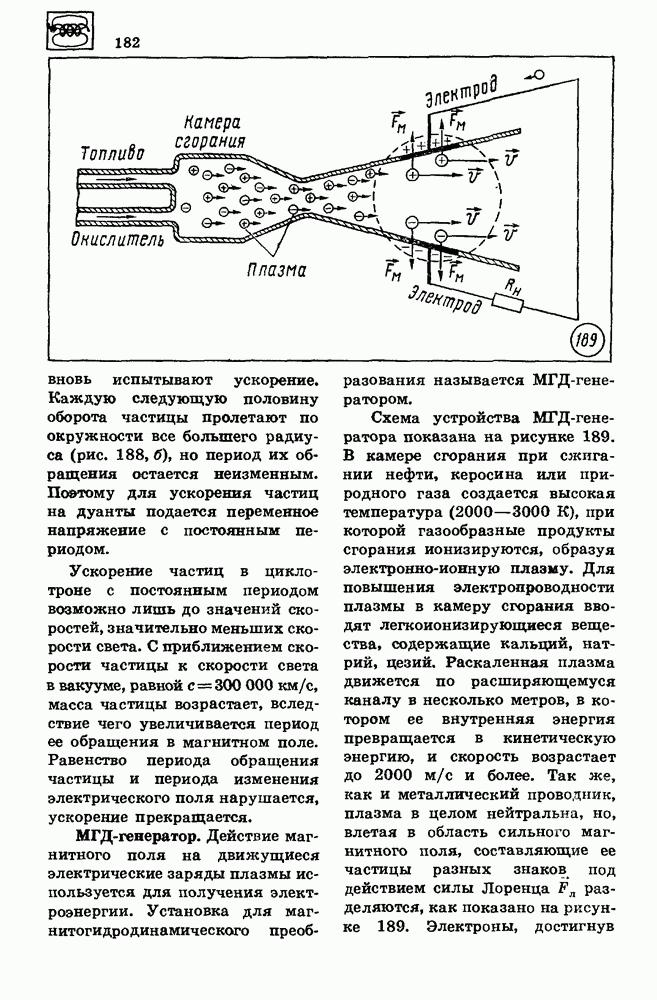
- 72. ТРАНСФОРМАТОР
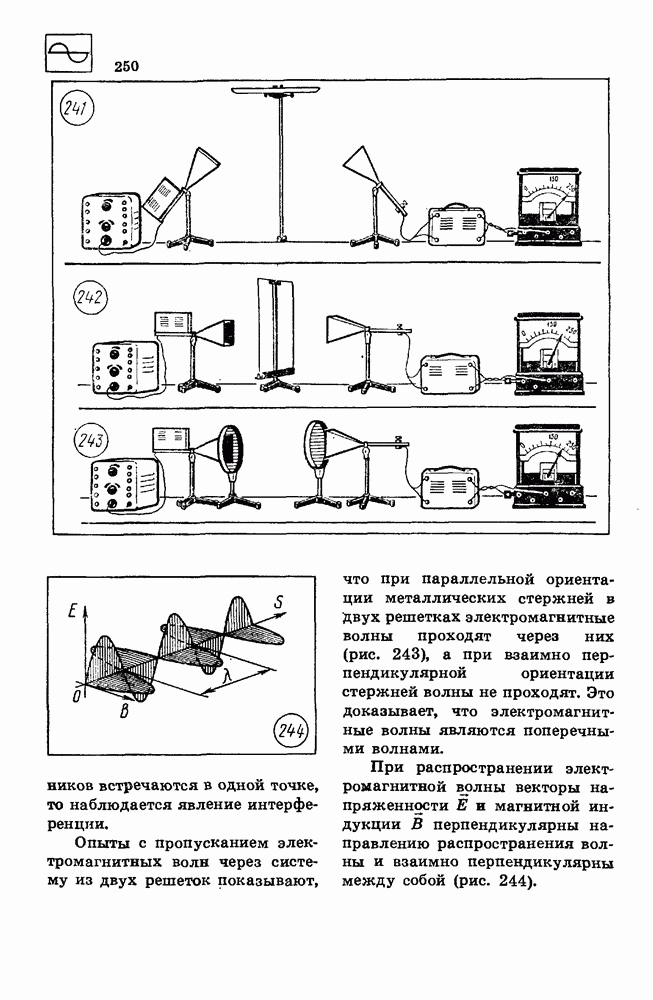
- 73. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
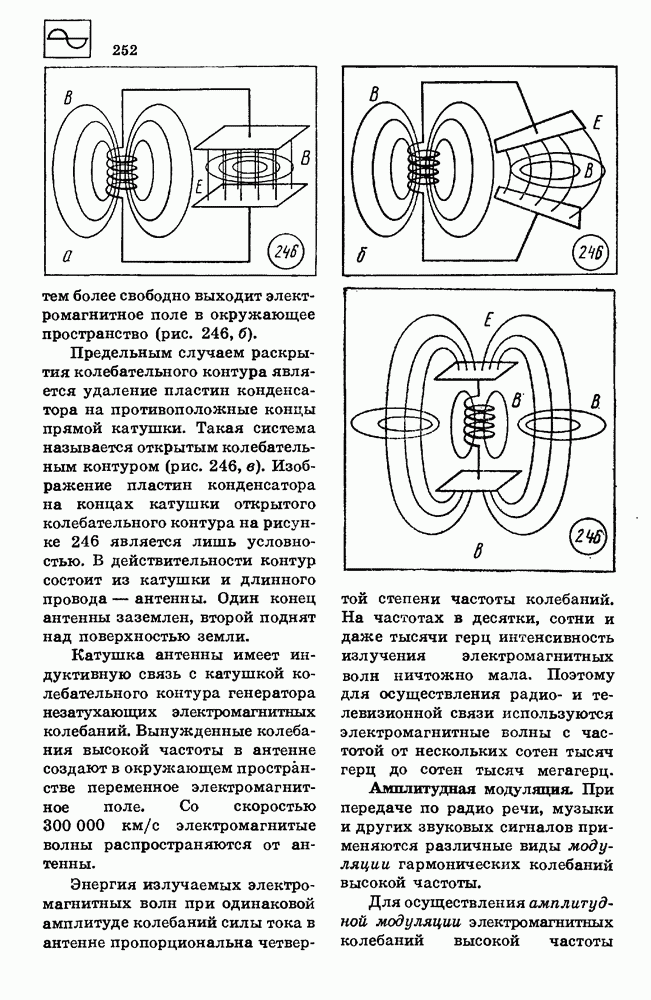
- 74. ПРИНЦИПЫ РАДИОСВЯЗИ
- 75. ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 76. РАЗВИТОЕ ПРЕДСТАВЛЕНИИ О ПРИРОДЕ СВЕТА
- 77. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
- 78. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 79. ОПТИЧЕСКИЕ ПРИБОРЫ
- 80. СПЕКТР ЭЛЕКТРОМАГНИТНЫХ ИЗЛУЧЕНИЙ
- 81. ЭЛЕМЕНТЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 82. КВАНТОВЫЕ СВОЙСТВА СВЕТА
- 83. ДОКАЗАТЕЛЬСТВА СЛОЖНОЙ СТРУКТУРЫ АТОМОВ
- 84. КВАНТОВЫЕ ПОСТУЛАТЫ БОРА
- 86. АТОМНОЕ ЯДРО
- 87. РАДИОАКТИВНОСТЬ
- 88. СВОЙСТВА ЯДЕРНЫХ ИЗЛУЧЕНИЙ
- 89. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ РЕГИСТРАЦИИ ЗАРЯЖЕННЫХ ЧАСТИЦ
- 90. ЦЕПНАЯ РЕАКЦИЯ ДЕЛЕНИЯ ЯДЕР УРАНА
- 91. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- ПРИЛОЖЕНИЯ