| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
28. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
Используя зависимость давления идеального газа от его температуры и концентрации молекул

можно найти связь между основными макроскопическими параметрами газа — объемом V, его давлением  и температурой Т.
и температурой Т.
Концентрация  молекул газа равна
молекул газа равна

где  — число молекул газа в сосуде объемом V. Число
— число молекул газа в сосуде объемом V. Число  можно выразить как произведение количества вещества
можно выразить как произведение количества вещества  на постоянную Авогадро
на постоянную Авогадро 

Из выражений (25.9), (26.1) и (26.2) получаем

Произведение постоянной Авогадро  на постоянную Больцмана
на постоянную Больцмана  называется молярной газовой постоянной
называется молярной газовой постоянной  Молярная газовая постоянная равна
Молярная газовая постоянная равна

Используя молярную газовую постоянную, выражение (26.3) преобразуем в уравнение

Количество вещества  можно найти, зная массу вещества
можно найти, зная массу вещества  и его молярную массу М:
и его молярную массу М:

поэтому уравнение (26.5) можно записать в такой форме:

Это уравнение называется уравнением состояния идеального газа.
Уравнение, устанавливающее связь между давлением, объемом и температурой газов, было получено французским физиком Бенуа Клапейроном (1799—1864). В форме (26.7) его впервые применил великий русский ученый Дмитрий Иванович Менделеев (1834—1907), поэтому уравнение состояния газа называется уравнением Менделеева — Клапейрона.
Для исследования связи между объемом, давлением и температурой газа можно использовать герметичный сосуд, объем которого может изменяться. Внешний вид такого прибора — сильфона — представлен на рисунке 87.
Изопроцессы в газах.
Уравнение (26.7) показывает, что возможно одновременное изменение пяти параметров, характеризующих состояние идеального газа. Однако многие процессы в газах, происходящие в природе и осуществляемые в технике, можно рассматривать приближенно как процессы, в которых изменяются лишь два лараметра из пяти. Особую роль в физике и технике играют три процесса — изотермический,

изохорный и изобарный. Рассмотрим эти процессы.
Изотермический процесс.
Изотермическим процессом называется процесс, протекающий при постоянной температуре Т. Из уравнения состояния идеального газа (26.7) следует, что при постоянной температуре Т и неизменных значениях массы газа и его молярной массы М произведение давления  газа на его объем V должно оставаться постоянным:
газа на его объем V должно оставаться постоянным:

Изотермический процесс можно осуществить, например, путем изменения объема газа при постоянной температуре.
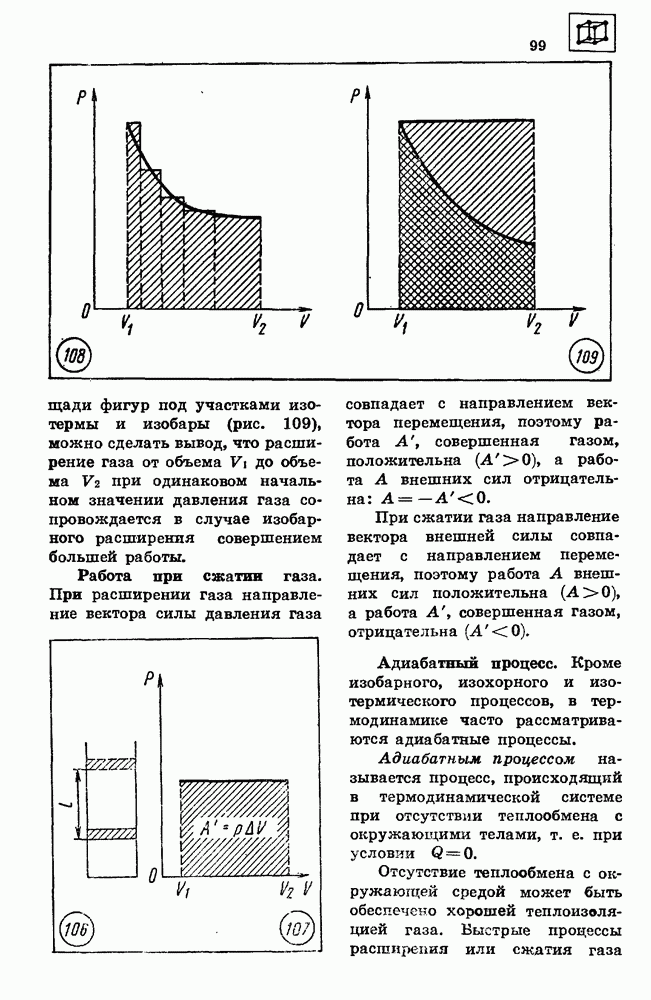
График изотермического процесса называется изотермой. Изотерма, изображенная в прямоугольной системе координат, по оси ординат которой отсчитывается давление газа, а по оси абсцисс — его объем, является гиперболой (рис. 88).
Уравнение (26.8), устанавливающее связь между давлением и объемом газа при постоянной температуре, было получено из эксперимента до создания молекулярно-кинетической теории газов в  английским физиком Робертом Бойлем (1627—1691) и в
английским физиком Робертом Бойлем (1627—1691) и в  французским физиком
французским физиком  Мариоттом (1620—1684). Поэтому это уравнение называют законом Бойля — Мариотта.
Мариоттом (1620—1684). Поэтому это уравнение называют законом Бойля — Мариотта.

Изохорный процесс.
Изохорным процессом называется процесс, протекающий при неизменном объеме V и условии 
При этих условиях из уравнения состояния идеального газа (26.7) для двух значений температуры То и Т следует

или

Если  выбрать равным 273 К (0 °С), то
выбрать равным 273 К (0 °С), то 
Обозначив  получим уравнение для изохорного процесса
получим уравнение для изохорного процесса

где  — давление газа при абсолютной температуре
— давление газа при абсолютной температуре  — давление газа при температуре
— давление газа при температуре  а — температурный коэффициент давления газа, равный
а — температурный коэффициент давления газа, равный

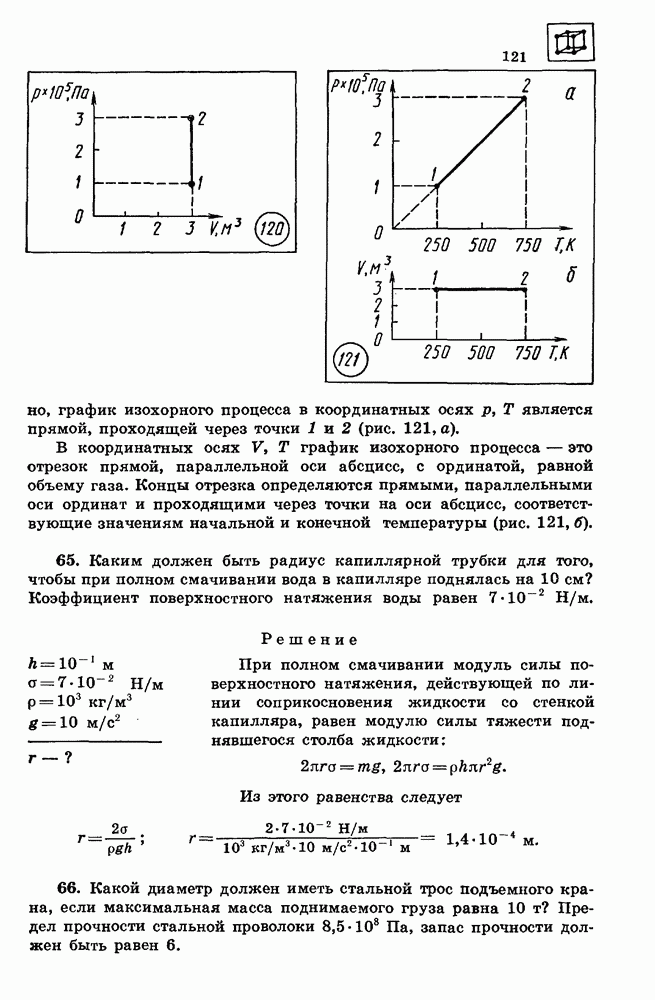
График уравнения изохорного процесса называется изохорой. Изохора, изображенная в прямоугольной системе координат, по оси ординат которой


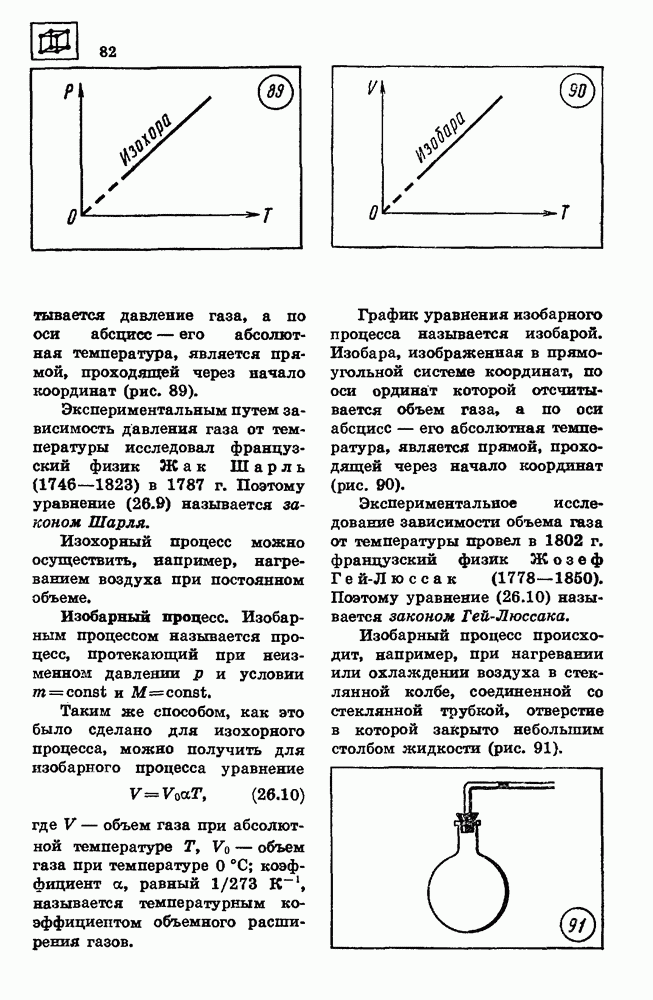
отсчитывается давление газа, а по оси абсцисс — его абсолютная температура, является прямой, проходящей через начало координат (рис. 89).
Экспериментальным путем зависимость давления газа от температуры исследовал французский физик Жак Шарль (1746—1823) в 1787 г. Поэтому уравнение (26.9) называется законом Шарля.
Изохорный процесс можно осуществить, например, нагреванием воздуха при постоянном объеме.
Изобарный процесс.
Изобарным процессом называется процесс, протекающий при неизменном давлении  и условии
и условии 
Таким же способом, как это было сделано для изохорного процесса, можно получить для изобарного процесса уравнение

где V — объем газа при абсолютной температуре  — объем газа при температуре
— объем газа при температуре  коэффициент а, равный
коэффициент а, равный  называется температурным коэффициентом объемного расширения газов.
называется температурным коэффициентом объемного расширения газов.
График уравнения изобарного процесса называется изобарой. Изобара, изображенная в прямоугольной системе координат, по оси ординат которой отсчитывается объем газа, а по оси абсцисс — его абсолютная температура, является прямой, проходящей через начало координат (рис. 90).
Экспериментальное исследование зависимости объема газа от температуры провел в 1802 г. французский физик Жозеф Гей-Люссак (1778—1860). Поэтому уравнение (26.10) называется законом Гей-Люссака.
Изобарный процесс происходит, например, при нагревании или охлаждении воздуха в стеклянной колбе, соединенной со стеклянной трубкой, отверстие в которой закрыто небольшим столбом жидкости (рис. 91).

| << Предыдущий параграф | Следующий параграф >> |
- 1. МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ
- 2. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- 3. РАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
- 4. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- 5. МАССА ТЕЛА
- 6. СИЛА
- 7. ВТОРОЙ ЗАКОН НЬЮТОНА
- 8. ТРЕТИЙ ЗАКОН НЬЮТОНА
- 9. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
- 10. ВЕС И НЕВЕСОМОСТЬ
- 11. ДВИЖЕНИЕ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- 12. СИЛА УПРУГОСТИ
- 13. СИЛЫ ТРЕНИЯ
- 14. УСЛОВИЯ РАВНОВЕСИЯ ТЕЛ
- 15. ЭЛЕМЕНТЫ ГИДРОСТАТИКИ
- 16. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- 17. РЕАКТИВНОЕ ДВИЖЕНИЕ
- 18. МЕХАНИЧЕСКАЯ РАБОТА
- 19. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- 20. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
- 21. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ В МЕХАНИЧЕСКИХ ПРОЦЕССАХ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 22. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОИ ТЕОРИИ И ИХ ОПЫТНОЕ ОБОСНОВАНИЕ
- 23. МАССА МОЛЕКУЛ
- 24. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОИ ТЕОРИИ ИДЕАЛЬНОГО ГАЗА
- 25. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- 28. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- 27. СВОЙСТВА ЖИДКОСТЕЙ
- 28. ИСПАРЕНИЕ И КОНДЕНСАЦИЯ
- 29. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА
- 30. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ЦЕЛ
- 31. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 32. КОЛИЧЕСТВО ТЕПЛОТЫ
- 33. РАБОТА ПРИ ИЗМЕНЕНИИ ОБЪЕМА ГАЗА
- 34. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДБИГАТЕЛЕЙ
- 35. ТЕПЛОВЫЕ МАШИНЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 36. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- 37. ЗАКОН КУЛОНА
- 38. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
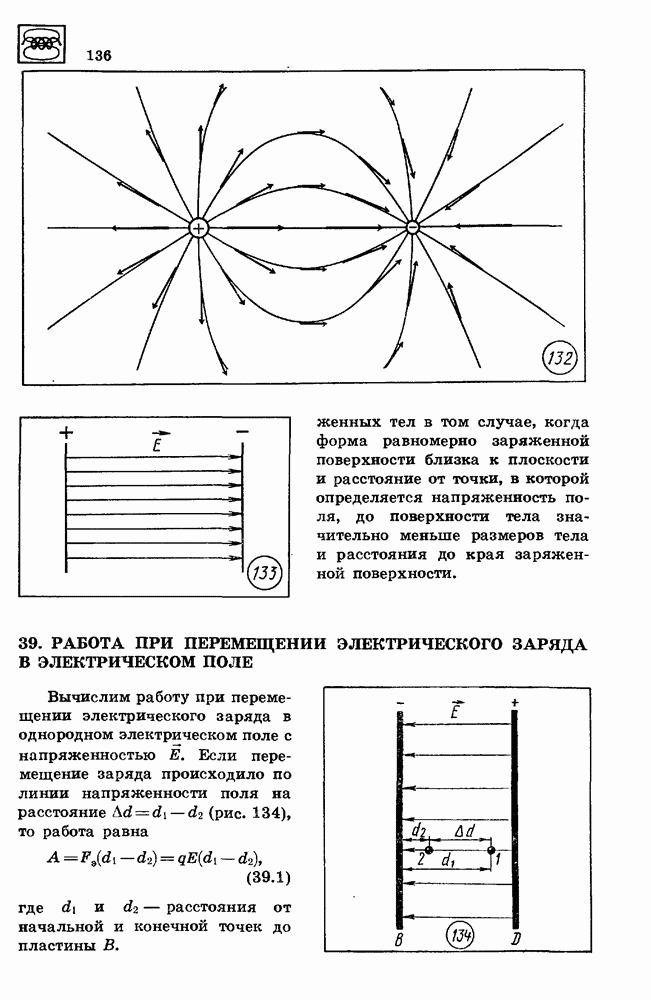
- 39. РАБОТА ПРИ ПЕРЕМЕЩЕНИИ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- 40. ПОТЕНЦИАЛ
- 41. ВЕЩЕСТВО В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- 42. ЭЛЕКТРОЕМКОСТЬ
- 43. ЗАКОН ОМА
- 44. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ
- 45. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- 46. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ
- 47. ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
- 48. ОТКРЫТИЕ ЭЛЕКТРОНА
- 49. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ
- 50. ЭЛЕКТРИЧЕСКИИ ТОК В ВАКУУМЕ
- 51. МАГНИТНОЕ ПОЛЕ
- 52. СИЛА ЛОРЕНЦА
- 53. ВЕЩЕСТВО В МАГНИТНОМ ПОЛЕ
- 54. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- 55. САМОИНДУКЦИЯ
- 56. МАГНИТНАЯ ЗАПИСЬ ИНФОРМАЦИИ
- 57. МАШИНА ПОСТОЯННОГО ТОКА
- 58. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 59. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
- 60. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
- 61. ПРЕВРАЩЕНИЯ ЭНЕРГИИ ПРИ МЕХАНИЧЕСКИХ КОЛЕБАНИЯХ
- 62. РАСПРОСТРАНЕНИЕ КОЛЕБАНИИ В УПРУГОЙ СРЕДЕ
- 63. ЗВУКОВЫЕ ВОЛНЫ
- 64. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ВОЛН
- 65. ИНТЕРФЕРЕНЦИЯ, ДИФРАКЦИЯ И ПОЛЯРИЗАЦИЯ ВОЛН
- 66. СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
- 67. АВТОКОЛЕБАТЕЛЬНЫЙ ГЕНЕРАТОР НЕЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИИ
- 68. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- 69. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 70. ИНДУКТИВНОСТЬ И ЕМКОСТЬ В ЦКТТИ ПЕРЕМЕННОГО ТОКА
- 71. РЕЗОНАНС В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
- 72. ТРАНСФОРМАТОР
- 73. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- 74. ПРИНЦИПЫ РАДИОСВЯЗИ
- 75. ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 76. РАЗВИТОЕ ПРЕДСТАВЛЕНИИ О ПРИРОДЕ СВЕТА
- 77. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
- 78. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 79. ОПТИЧЕСКИЕ ПРИБОРЫ
- 80. СПЕКТР ЭЛЕКТРОМАГНИТНЫХ ИЗЛУЧЕНИЙ
- 81. ЭЛЕМЕНТЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 82. КВАНТОВЫЕ СВОЙСТВА СВЕТА
- 83. ДОКАЗАТЕЛЬСТВА СЛОЖНОЙ СТРУКТУРЫ АТОМОВ
- 84. КВАНТОВЫЕ ПОСТУЛАТЫ БОРА
- 86. АТОМНОЕ ЯДРО
- 87. РАДИОАКТИВНОСТЬ
- 88. СВОЙСТВА ЯДЕРНЫХ ИЗЛУЧЕНИЙ
- 89. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ РЕГИСТРАЦИИ ЗАРЯЖЕННЫХ ЧАСТИЦ
- 90. ЦЕПНАЯ РЕАКЦИЯ ДЕЛЕНИЯ ЯДЕР УРАНА
- 91. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- ПРИЛОЖЕНИЯ