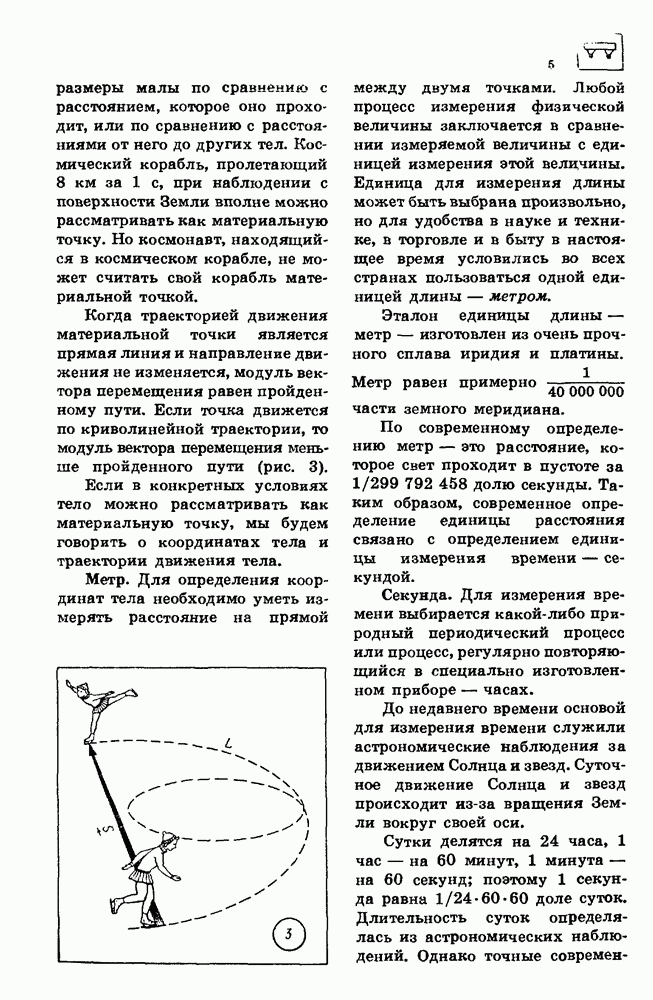
3. РАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ

Среди различных видов криволинейного движения особый интерес представляет равномерное движение тела по окружности. Это самый простой вид криволинейного движения. Вместе с тем любое сложное криволинейное движение тела на достаточно малом участке его траектории можно приближенно рассматривать как равномерное движение по окружности.

Центростремительное ускорение.

При равномерном движении по окружности значение скорости остается постоянным, а направление вектора скорости изменяется в процессе движения. Определим ускорение тела, движущегося равномерно по окружности радиусом За интервал времени тело проходит путь

Этот путь равен длине дуги (рис. 17). Векторы скоростей в точках А и В направлены по касательным к окружности в этих точках, угол а между векторами равен углу между радиусами и

Для нахождения вектора ускорения а нужно найти разность векторов скорости и определить отношение изменения скорости к малому интервалу времени за который произошло это изменение:

Из подобия треугольников и следует

Если интервал времени мал, то мал и угол а. При малых значениях угла а длина хорды примерно равна длине дуги т. е. Так как то из выражения (3.1) получаем

Поскольку

из выражений (3.3) и (3.4) получаем

Из рисунка 17 видно, что, чем меньше угол а, тем ближе направление вектора к направлению на центр окружности. Так как вектор ускорения а равен отношению вектора к интервалу времени при условии, что интервал времени очень мал, то вектор ускорения при равномерном движении по окружности направлен к ее центру.

При изменении положения тела на окружности меняется направление на центр окружности. Следовательно, при равномерном движении тела по окружности модуль ускорения имеет постоянное значение, но направление вектора ускорения изменяется со временем. Ускорение при равномерном движении по окружности называется центростремительным ускорением.

Период и частота.

Промежуток времени, за который тело совершает полный оборот при движении по окружности, называется периодом. Период обращения тела по окружности обозначается буквой Т. Так как длина окружности равна период обращения при равномерном движении тела со скоростью по окружности радиусом равняется

Величина, обратная периоду обращения, называется частотой обращения. Частота обращения обозначается греческой буквой и показывает, сколько оборотов по окружности совершает тело в единицу времени:

Единица частоты —

Используя формулы (3.5), (3.6) и (3.7), можно получить формулы для вычисления центростремительного ускорения:

и