| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
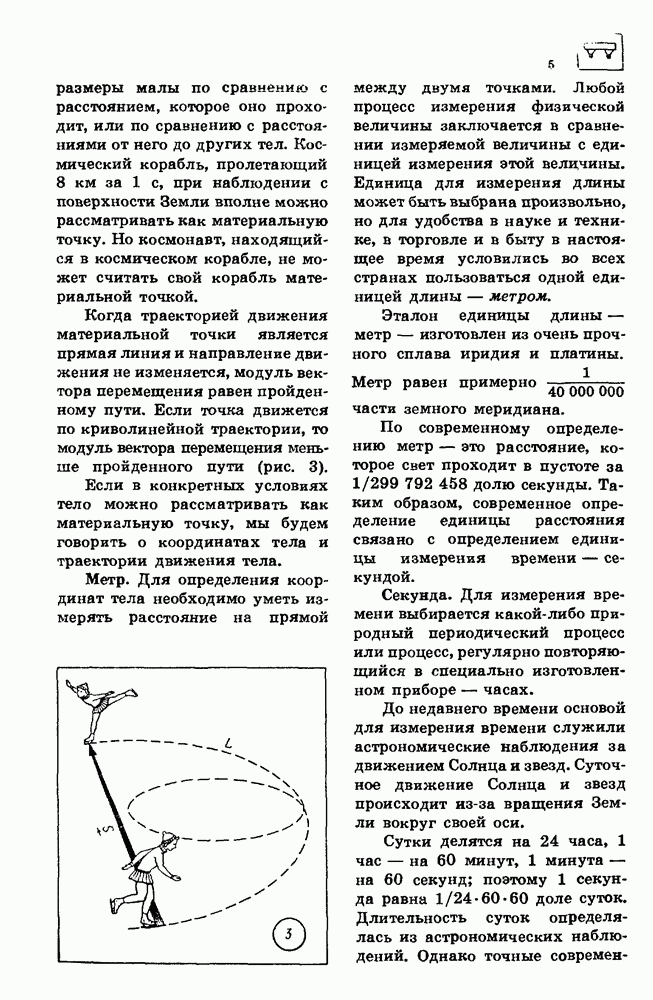
60. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Гармонические колебания.
Гармоническими колебаниями называют колебания, описываемые уравнением

Здесь х — смещение тела от положения равновесия,  — циклическая частота колебаний,
— циклическая частота колебаний,  — время.
— время.
Амплитуда и фаза колебаний.
Модуль максимального смещения  тела от положения равновесия называется амплитудой колебаний. Величина, стоящая под знаком косинуса, называется фазой
тела от положения равновесия называется амплитудой колебаний. Величина, стоящая под знаком косинуса, называется фазой  гармонического колебания:
гармонического колебания:

Фаза колебаний  в начальный момент времени
в начальный момент времени  называется начальной фазой.
называется начальной фазой.
Скорость и ускорение при гармонических колебаниях.
Найдем, как зависят от времени скорость и ускорение тела, совершающего гармонические колебания по закону

вдоль координатной оси  Скорость
Скорость  движения тела определяется выражением
движения тела определяется выражением

Более строго проекция скорости поступательного движения тела на ось  определяется как производная координаты х по времени:
определяется как производная координаты х по времени:

Для определения проекции ускорения движения тела в любой момент времени необходимо найти производную от проекции скорости  по времени
по времени 

Гармонические колебания под действием силы упругости.
Из уравнений (60.3) и (60.5) следует, что

При гармонических колебаниях тела вдоль оси  ускорение прямо пропорционально смещению х тела от положения равновесия.
ускорение прямо пропорционально смещению х тела от положения равновесия.
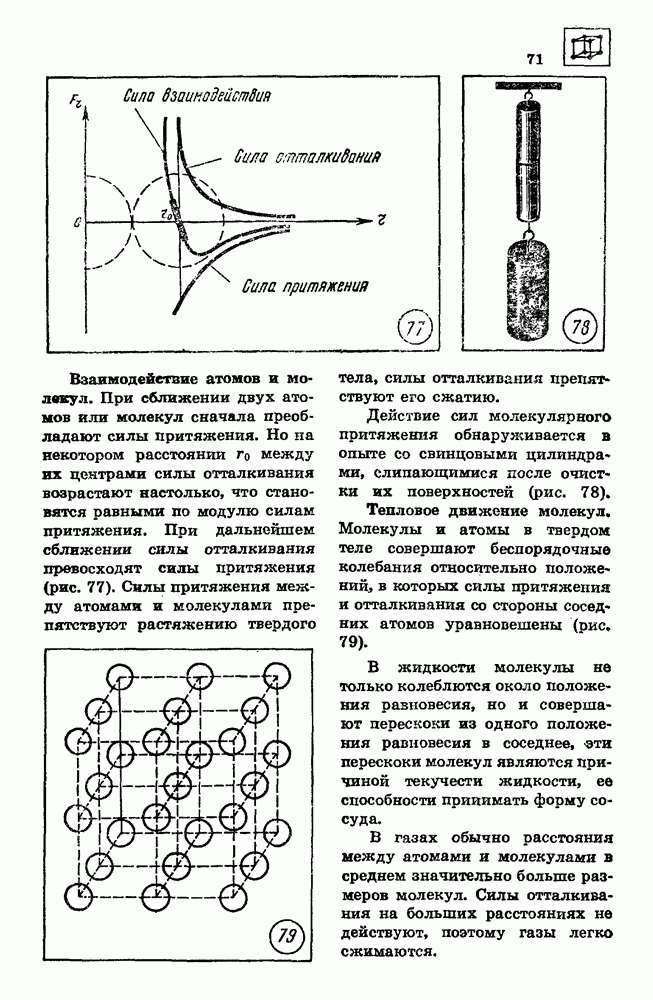
Примером силы, пропорциональной смещению тела, является сила упругости. По закону Гука сила упругости прямо пропорциональна деформации х тела:

Действие силы упругости может вызывать возникновение гармонических колебаний. Примером гармонических колебаний, возникающих под действием силы упругости, могут служить колебания груза, подвешенного на стальной пружине, колебания струны.
Если тело массой  совершает под действием силы упругости гармонические колебания с циклической частотой со, то, применив второй закон Ньютона для проекции ускорения
совершает под действием силы упругости гармонические колебания с циклической частотой со, то, применив второй закон Ньютона для проекции ускорения  получим
получим

С другой стороны, ускорение при гармонических колебаниях с циклической частотой со определяется в любой момент времени выражением (60.6). Из выражений (60.6) и (60.7) устанавливается связь между циклической частотой со, жесткостью к деформируемого тела и массой  тела:
тела:

Математический маятник.
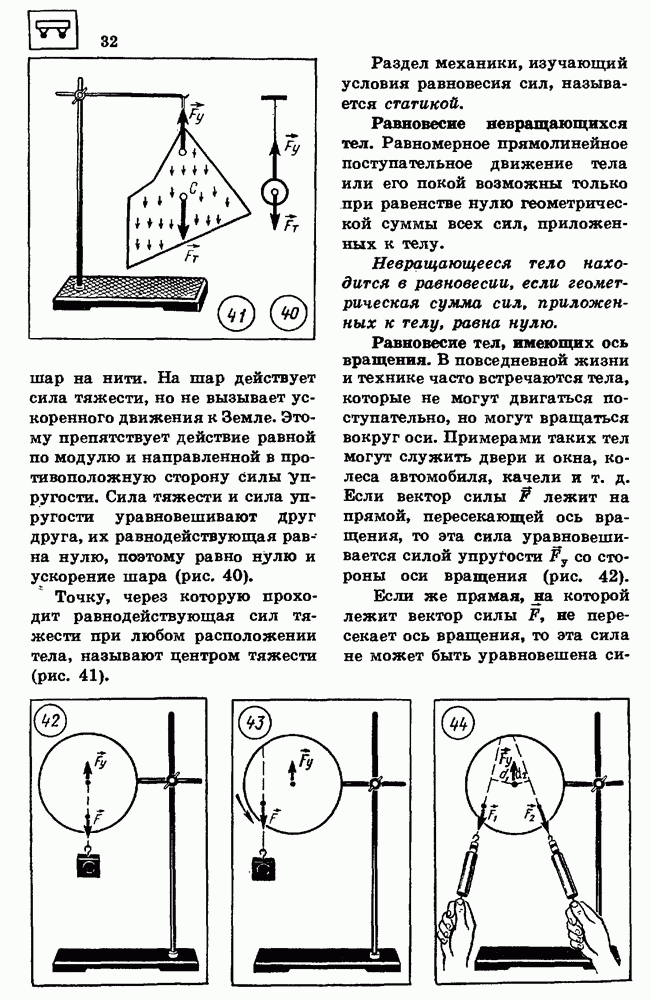
Тело небольших размеров, подвешенное на нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела, называют математическим маятником. При вертикальном положении нити действие силы тяжести  уравновешивается действием силы упругости
уравновешивается действием силы упругости  Это положение является положением равновесия.
Это положение является положением равновесия.

При малых отклонениях маятника от положения равновесия возникает равнодействующая сил тяжести и упругости, направленная к положению равновесия (рие. 216), и его колебания - являются гармоническими. Период колебаний равен

Зависимость периода колебаний маятника от ускорения свободного падения используется для точных измерений ускорения свободного падения на поверхности Земли. По результатам измерений можно обнаружить районы залегания полезных ископаемых — железной руды, нефти, газа.
| << Предыдущий параграф | Следующий параграф >> |
- 1. МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ
- 2. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- 3. РАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
- 4. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- 5. МАССА ТЕЛА
- 6. СИЛА
- 7. ВТОРОЙ ЗАКОН НЬЮТОНА
- 8. ТРЕТИЙ ЗАКОН НЬЮТОНА
- 9. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
- 10. ВЕС И НЕВЕСОМОСТЬ
- 11. ДВИЖЕНИЕ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- 12. СИЛА УПРУГОСТИ
- 13. СИЛЫ ТРЕНИЯ
- 14. УСЛОВИЯ РАВНОВЕСИЯ ТЕЛ
- 15. ЭЛЕМЕНТЫ ГИДРОСТАТИКИ
- 16. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- 17. РЕАКТИВНОЕ ДВИЖЕНИЕ
- 18. МЕХАНИЧЕСКАЯ РАБОТА
- 19. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- 20. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
- 21. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ В МЕХАНИЧЕСКИХ ПРОЦЕССАХ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 22. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОИ ТЕОРИИ И ИХ ОПЫТНОЕ ОБОСНОВАНИЕ
- 23. МАССА МОЛЕКУЛ
- 24. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОИ ТЕОРИИ ИДЕАЛЬНОГО ГАЗА
- 25. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- 28. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- 27. СВОЙСТВА ЖИДКОСТЕЙ
- 28. ИСПАРЕНИЕ И КОНДЕНСАЦИЯ
- 29. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА
- 30. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ЦЕЛ
- 31. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 32. КОЛИЧЕСТВО ТЕПЛОТЫ
- 33. РАБОТА ПРИ ИЗМЕНЕНИИ ОБЪЕМА ГАЗА
- 34. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДБИГАТЕЛЕЙ
- 35. ТЕПЛОВЫЕ МАШИНЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 36. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- 37. ЗАКОН КУЛОНА
- 38. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 39. РАБОТА ПРИ ПЕРЕМЕЩЕНИИ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- 40. ПОТЕНЦИАЛ
- 41. ВЕЩЕСТВО В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- 42. ЭЛЕКТРОЕМКОСТЬ
- 43. ЗАКОН ОМА
- 44. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ
- 45. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- 46. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ
- 47. ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
- 48. ОТКРЫТИЕ ЭЛЕКТРОНА
- 49. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ
- 50. ЭЛЕКТРИЧЕСКИИ ТОК В ВАКУУМЕ
- 51. МАГНИТНОЕ ПОЛЕ
- 52. СИЛА ЛОРЕНЦА
- 53. ВЕЩЕСТВО В МАГНИТНОМ ПОЛЕ
- 54. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- 55. САМОИНДУКЦИЯ
- 56. МАГНИТНАЯ ЗАПИСЬ ИНФОРМАЦИИ
- 57. МАШИНА ПОСТОЯННОГО ТОКА
- 58. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 59. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
- 60. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
- 61. ПРЕВРАЩЕНИЯ ЭНЕРГИИ ПРИ МЕХАНИЧЕСКИХ КОЛЕБАНИЯХ
- 62. РАСПРОСТРАНЕНИЕ КОЛЕБАНИИ В УПРУГОЙ СРЕДЕ
- 63. ЗВУКОВЫЕ ВОЛНЫ
- 64. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ВОЛН
- 65. ИНТЕРФЕРЕНЦИЯ, ДИФРАКЦИЯ И ПОЛЯРИЗАЦИЯ ВОЛН
- 66. СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
- 67. АВТОКОЛЕБАТЕЛЬНЫЙ ГЕНЕРАТОР НЕЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИИ
- 68. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- 69. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 70. ИНДУКТИВНОСТЬ И ЕМКОСТЬ В ЦКТТИ ПЕРЕМЕННОГО ТОКА
- 71. РЕЗОНАНС В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
- 72. ТРАНСФОРМАТОР
- 73. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- 74. ПРИНЦИПЫ РАДИОСВЯЗИ
- 75. ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 76. РАЗВИТОЕ ПРЕДСТАВЛЕНИИ О ПРИРОДЕ СВЕТА
- 77. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
- 78. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 79. ОПТИЧЕСКИЕ ПРИБОРЫ
- 80. СПЕКТР ЭЛЕКТРОМАГНИТНЫХ ИЗЛУЧЕНИЙ
- 81. ЭЛЕМЕНТЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 82. КВАНТОВЫЕ СВОЙСТВА СВЕТА
- 83. ДОКАЗАТЕЛЬСТВА СЛОЖНОЙ СТРУКТУРЫ АТОМОВ
- 84. КВАНТОВЫЕ ПОСТУЛАТЫ БОРА
- 86. АТОМНОЕ ЯДРО
- 87. РАДИОАКТИВНОСТЬ
- 88. СВОЙСТВА ЯДЕРНЫХ ИЗЛУЧЕНИЙ
- 89. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ РЕГИСТРАЦИИ ЗАРЯЖЕННЫХ ЧАСТИЦ
- 90. ЦЕПНАЯ РЕАКЦИЯ ДЕЛЕНИЯ ЯДЕР УРАНА
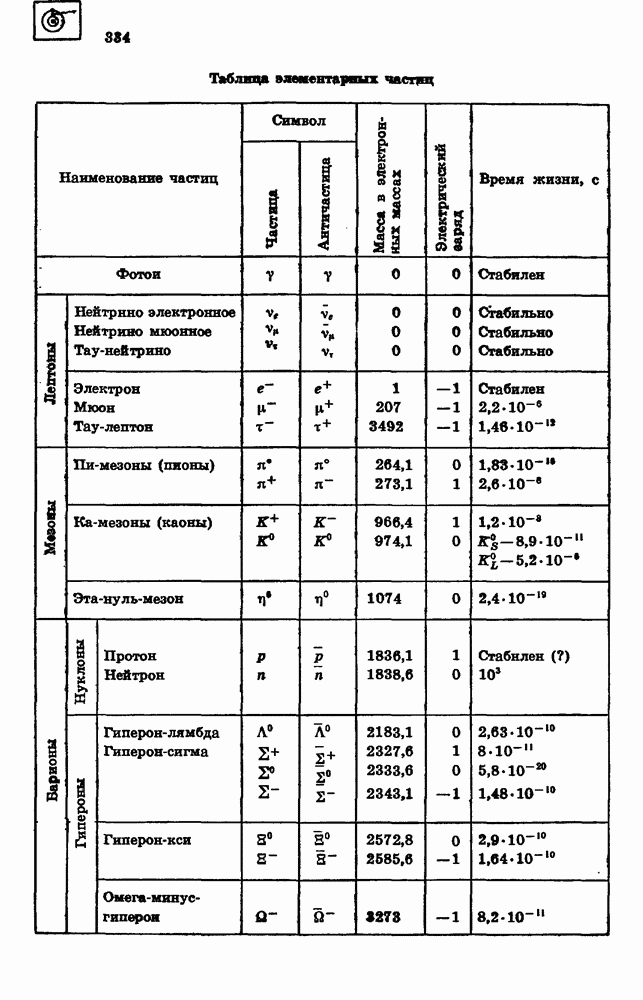
- 91. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- ПРИЛОЖЕНИЯ