ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

171. Определите красную границу фотоэффекта для металла с работой выхода 2 эВ.

Решение

Из уравнения Эйнштейна (82.4) для фотоэффекта при условии имеем

Частота света связана с его скоростью с и длиной волны X выражением с

Из этих двух формул получаем

172. Найдите максимальную скорость электронов, освобождаемых при фотоэффекте светом с Длиной волны с поверхности материала с работой выхода 1,9 эВ.

Решение

Для решения задачи воспользуемся уравнением Эйнштейна для фотоэффекта (82.4), подставив в него выражение для максимальной кинетической энергии электронов:

173. Определите работу выхода электрона с поверхности фотокатода и красную границу фотоэффекта, если при облучении фотоэлемента светом с частотой Гц фототок прекращается при запирающем напряжении 4,1 В.

Решение

Используем условие запирания фототока:

С учетом этого условия уравнение Эйнштейна для фотоэффекта будет иметь вид

Определим красную границу фотоэффекта:

174. При бомбардировке электронами атомы ртути переходят в возбужденное состояние, если анергия электронов равна 4,9 эВ или превышает это значение. Рассчитайте длину волны света, испускаемого атомом ртути при переходе из первого возбужденного состояния в нормальное.

Решение

Используем связь между энергией фотона и частотой: отсюда

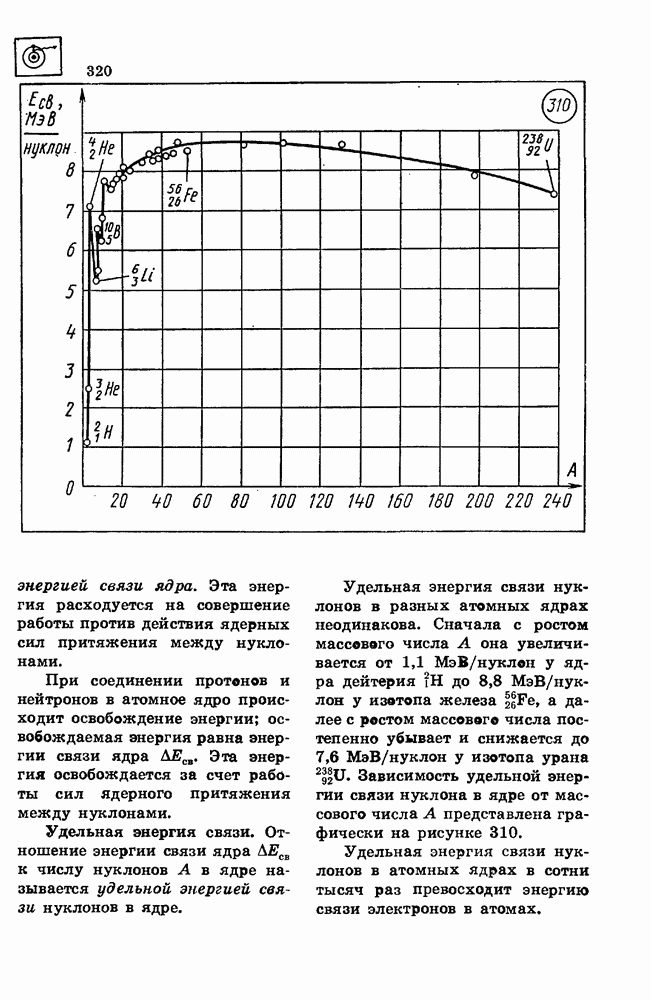
175. Вычислите эпергию связи ядра атома дейтерия.

Решение

Энергия связи ядра равна

где — разность суммы масс свободных частиц, входящих в состав ядра, и массы ядра; с — скорость света в вакууме. Для нахождения разности масс отыскиваем в справочнике по физике сведения о массах протона нейтрона и электрона те и атома дейтерия Для нахождения массы ядра дейтерия необходимо вычесть из массы атома дейтерия массу электрона, находящегося на его оболочке:

Но 1 а.е.м. кг, поэтому

176. Вычислите энергетический выход ядерной реакции

Для вычисления энергетического выхода ядерной реакции необходимо найти разность масс частиц, вступающих в реакцию, и частиц — продуктов реакции. В реакции участвуют атомные ядра, но в справочных таблицах обычно даются сведения лишь о массах атомов. Можно найти массу каждого атомного ядра вычитанием массы электронов оболочки из массы атома. Можно поступить иначе. Если в уравнении ядерной реакции слева и справа пользоваться только массами атомов (т. е. массой атома водорода, а не массой протона слева, и массой атома гелия, а не массой альфа-частицы справа), то из-за одинаковости числа электронов в атомах, вступающих в реакцию, и в продуктах реакции их вычитание осуществляется автоматически при нахождении разности масс. Таким образом, для решения задачи можно воспользоваться сведениями из справочника о массах атомов:

Вычислим энергетический выход при изменении массы на 1 а.е.м.:

Выход ядерной реакции равен

177. При осуществлении термоядерной реакции синтеза ядра гелия из ядер изотопов водорода — дейтерия и трития — по схеме

освобождается енергия 17,6 МэВ. Какая энергия освободится при синтезе 1 г гелия? Сколько каменного угля потребовалось бы сжечь для получения такой же энергии?

Решение

Для нахождения энергия, выделяющейся при синтезе гелия, нужно умножить выход ядерной реакции на число осуществленных реакций, равное числу атомов гелия в

Число атомов гелия равно

Поэтому для энергии Е получим

Из условия следует

Отсюда масса каменного угля, при сжигании которого освобождается столько же энергии, сколько и при синтезе гелия, равна

178. Определите второй продукт ядерной реакции

Решение

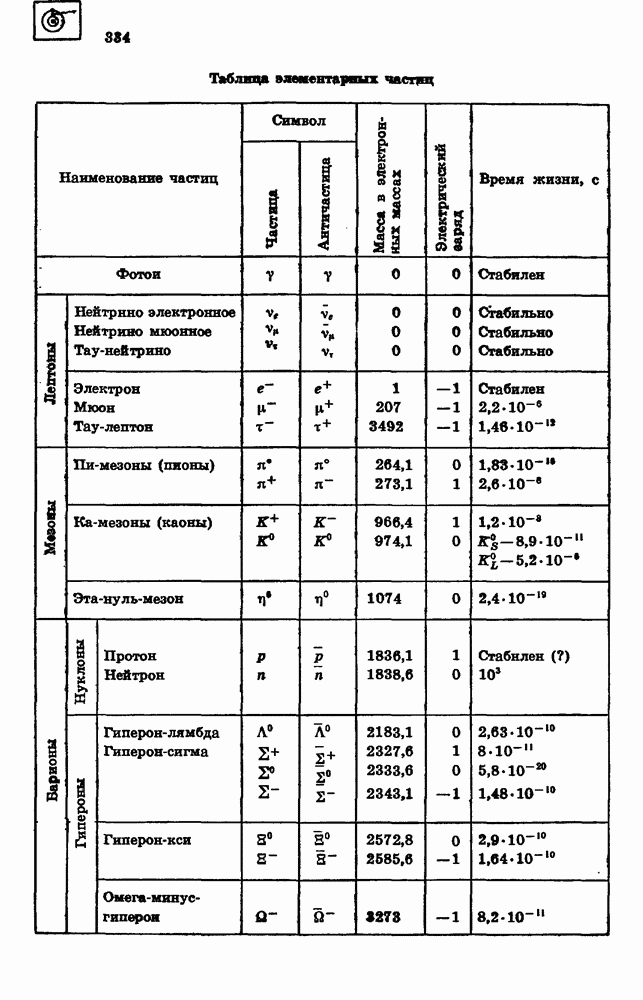
Для определения второго продукта ядерной реакции необходимо использовать тот факт, что при осуществлении ядерных реакций число барионов остается неизменным. Отсюда следует, что сумма протонов в частицах, вступающих в реакцию, должна быть равна сумме протонов в частицах — продуктах реакции, а общее число нуклонов в левой части уравнения равно общему числу нуклонов в правой его части. Число протонов в частицах, вступивших в данную ядерную реакцию, равно 3. В ядре гелия только Два протона, следовательно, во втором продукте ядерной реакции содержится один протон. Таким образом, второй продукт ядерной реакции является одним из изотопов водорода. Найдем массовое число этого изотопа. Общее число нуклонов в ядрах, представленных в левой части уравнения, равно 7. В ядре гелия четыре нуклона, следовательно, на долю второго продукта ядерной реакции приходится три нуклона. Таким образом, второй продукт ядерной реакции является изотопом водорода — тритием

179. Определите, какая частица участвует в осуществлении ядерной реакции

Решение

Воспользовавшись свойством сохранения числа протонов и общего числа нуклонов при осуществлении ядерных реакций, можно определить, что неизвестная частица X содержит два протона и состоит из четырех нуклонов. Следовательно, это ядро атома гелия (альф а-частица).

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

(см. скан)

(см. скан)