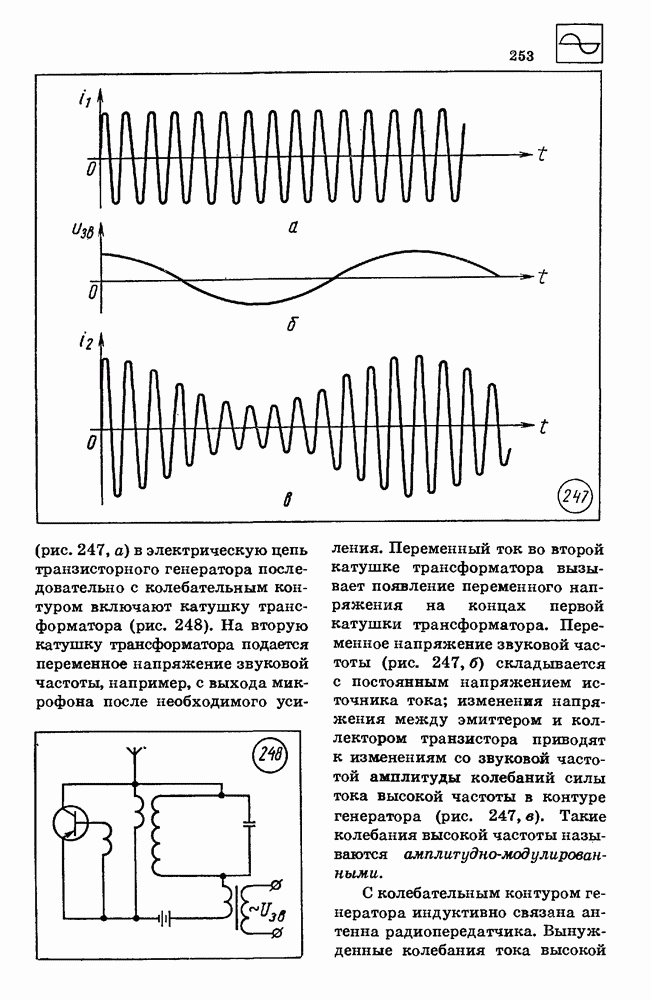
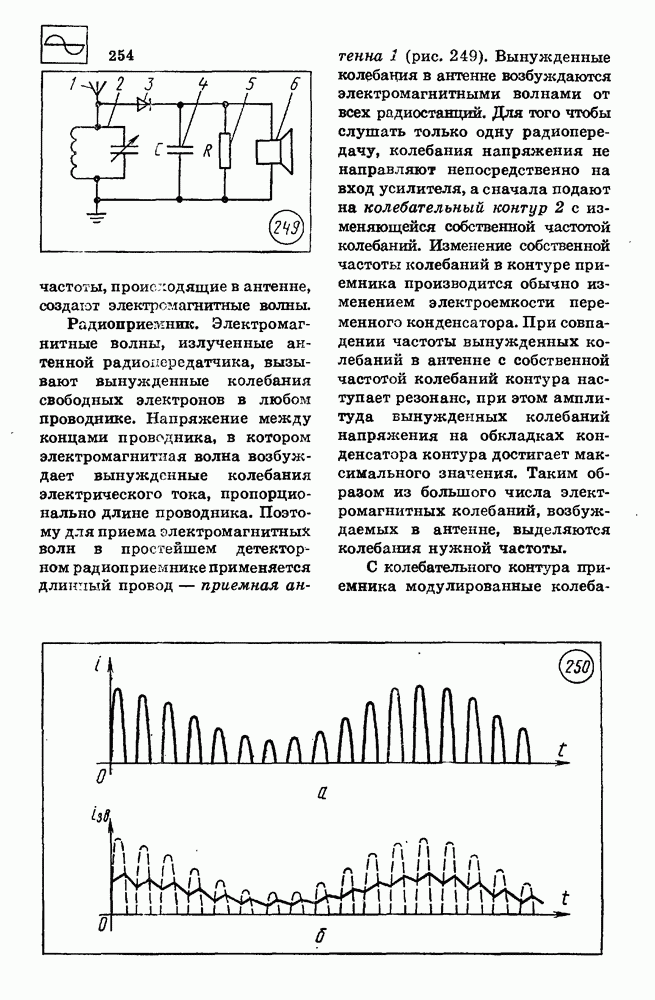
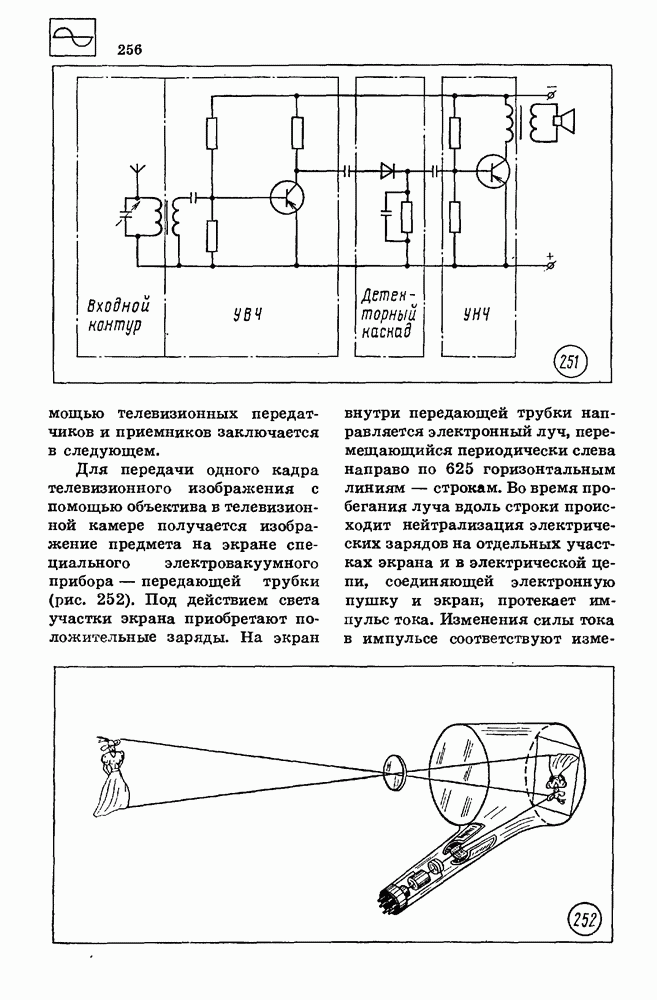
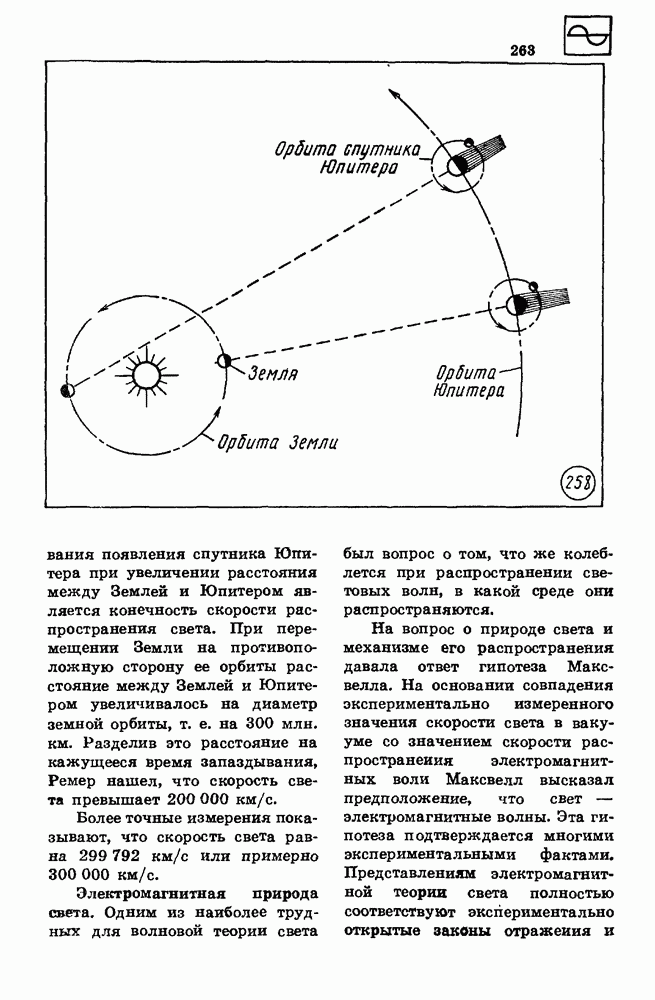
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
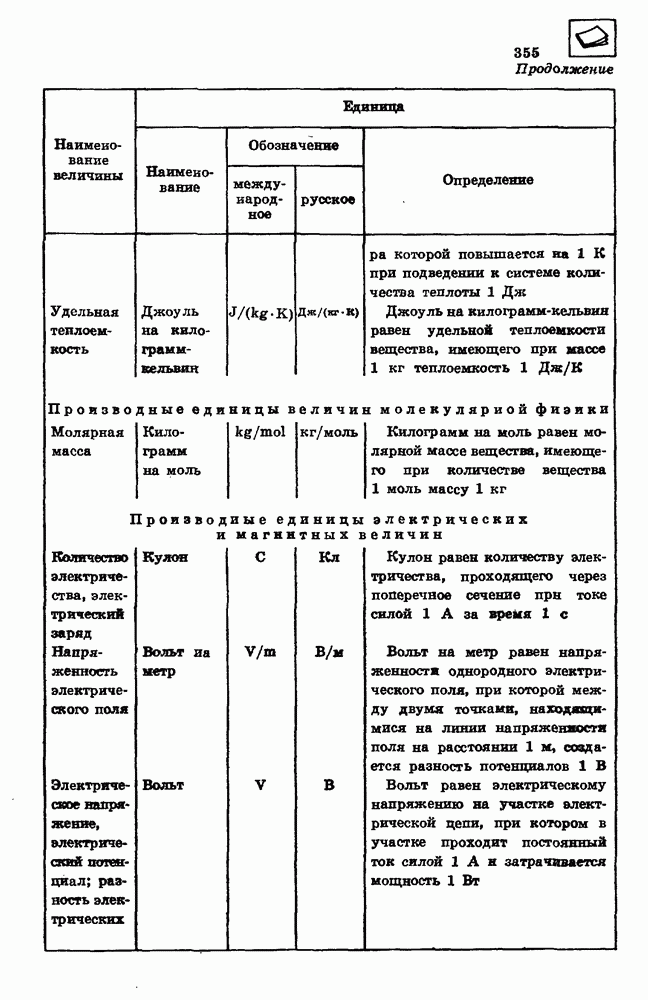
56. Какое давление на стенки сосудов оказывал бы идеальный газ с концентрацией 100 миллиардов молекул в кубическом миллиметре при средней квадратичной скорости движения молекул  и массе молекулы
и массе молекулы  кг?
кг?
Решение
Для вычисления давления идеального газа используем основное уравнение молекулярно-кинетической теории

Все величины необходимо выразить в единицах СИ:

Подставляя значения величин, получаем

Давление идеального газа с заданными параметрами оказывается в миллион раз меньше нормального атмосферного давления.
57. Считая воздух идеальным газом, оцените скорость теплового движения молекул газа при нормальных условиях.
Решение
Для решения задачи можно использовать основное уравнение молекулярно-кинетической теории

Так как произведение массы молекулы  на концентрацию молекул
на концентрацию молекул  равно плотности
равно плотности  газа, то давление идеального газа равно
газа, то давление идеального газа равно

где  — среднее значение квадрата скорости теплового движения молекул.
— среднее значение квадрата скорости теплового движения молекул.
Из этого уравнения следует, что для оценки скорости теплового движения молекул идеального газа можно использовать уравнение

Давление воздуха при нормальных условиях равно примерно  Па, плотность
Па, плотность  Подставляя эти значения, получаем
Подставляя эти значения, получаем

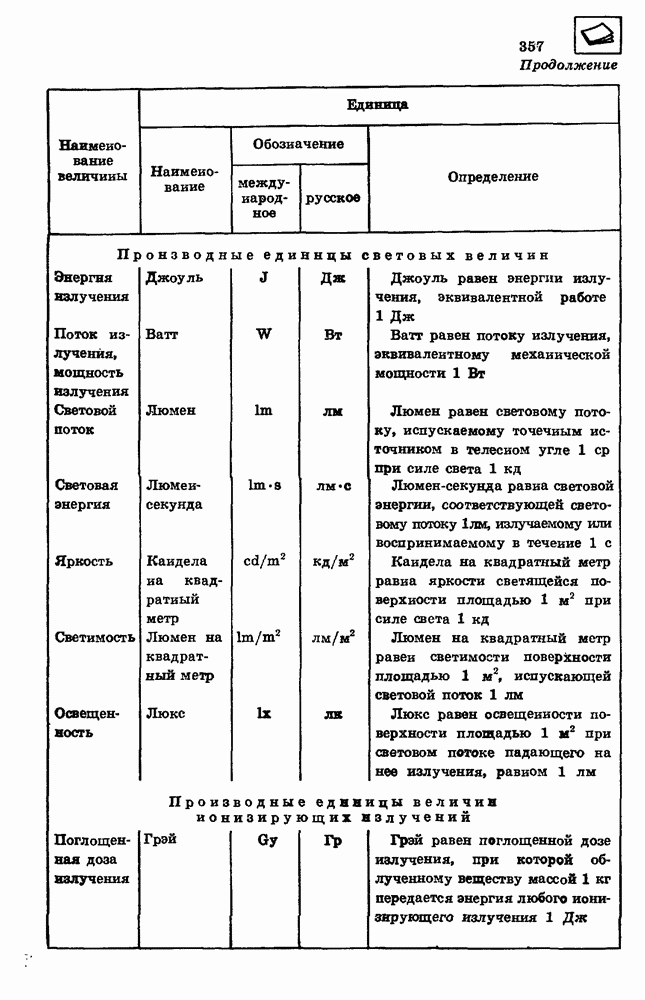
58. Вычислите среднюю кинетическую энергию молекул идеального газа при температуре 27 °С.
Решение
Средняя кинетическая энергия Е теплового движения молекул идеального газа связана с абсолютной температурой Т газа уравнением

где к — постоянная Больцмана. Для вычисления средней кинетической энергии молекул температуру газа по шкале Цельсия нужно перевести в температуру по абсолютной шкале:

Подставляя значения температуры и постоянной Больцмана, находим значение средней кинетической энергии молекул идеального газа:

59. В баллоне объемом  находится водород под давлением
находится водород под давлением  Па при температуре
Па при температуре  Определите массу газа, считая водород идеальным газом.
Определите массу газа, считая водород идеальным газом.
Решение
Для решения задачи воспользуемся уравнением состояния идеального газа

Из этого уравнения следует

где М — молярная масса газа; Т — его абсолютная температура. Выпишем в СИ значения всех величин и подставим их в расчетную формулу:

60. Какой объем занимает 2 моль идеального газа при условиях, соответствующих условиям в фотосфере Солнца? Температура фотосферы 6000 К, давление  Па.
Па.
Решение
Для решения задачи используем уравнение состояния идеального газа в форме

Объем газа из этого уравнения равен 
Выпишем численные значения величин в СИ и подставим их в расчетную формулу:

61. При температуре  и давлении
и давлении  Па объем воздушного шара, заполненного гелием, равен
Па объем воздушного шара, заполненного гелием, равен  Каким будет объем этого шара, если при подъеме в верхние слои атмосферы температура понизится до
Каким будет объем этого шара, если при подъеме в верхние слои атмосферы температура понизится до  а давление станет равным
а давление станет равным  Па? Массу гелия считать постоянной.
Па? Массу гелия считать постоянной.

Решение
Из уравнения состояния идеального газа

следует, что при условии 
Поэтому выполняется равенство

Из него получаем

62. Вычислите кинетическую энергию теплового движения всех молекул воздуха в физическом кабинете. Объем кабинета  давление воздуха —
давление воздуха —  Па. Сколько воды можно было бы нагреть от 0 до
Па. Сколько воды можно было бы нагреть от 0 до  при полном использовании этой энергии?
при полном использовании этой энергии?

Решение
Считая, что свойства воздуха близки к свойствам идеального газа, применим для вычисления кинетической энергии хаотического теплового движения всех его молекул формулу

Используя равенство  получим
получим

Так как из уравнения состояния идеального газа следует, что

то

Для вычисления массы нагреваемой воды запишем уравнение теплового баланса

и выразим из него массу 

По условию задачи  поэтому масса нагреваемой воды равна
поэтому масса нагреваемой воды равна

63. Как изменится объем пузырька воздуха при всплывании его со дна озера глубиной  к поверхности воды? Температура воды у дна озера и у поверхности одинакова. Атмосферное давление принять равным
к поверхности воды? Температура воды у дна озера и у поверхности одинакова. Атмосферное давление принять равным  Па.
Па.

Решение
Объем пузырька воздуха при всплывании будет изменяться из-за уменьшения давления. Так как температура воды одинакова у дна озера и у поверхности воды, изменение объема воздуха будет происходить в результате его изотермического расширения. При изотермическом процессе давление и объем газа связаны соотношением 
Отсюда 
Давление  поверхности воды равно внешнему атмосферному давлению. Давление
поверхности воды равно внешнему атмосферному давлению. Давление  на глубине
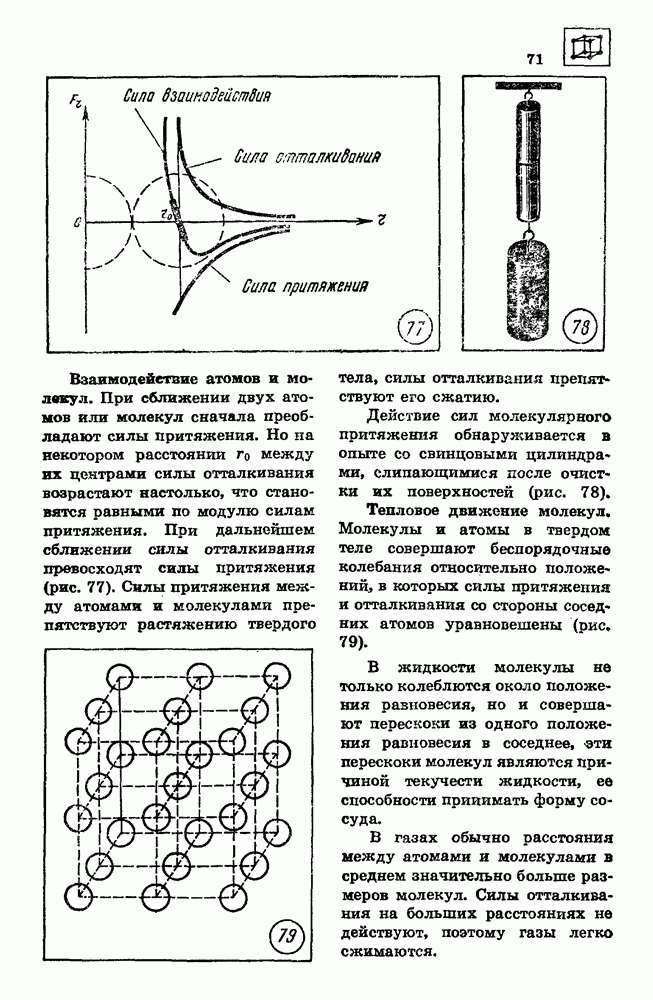
на глубине  складывается из внешнего атмосферного давления и давления водяного столба:
складывается из внешнего атмосферного давления и давления водяного столба: 
Подставляя численные значения величин, получаем 

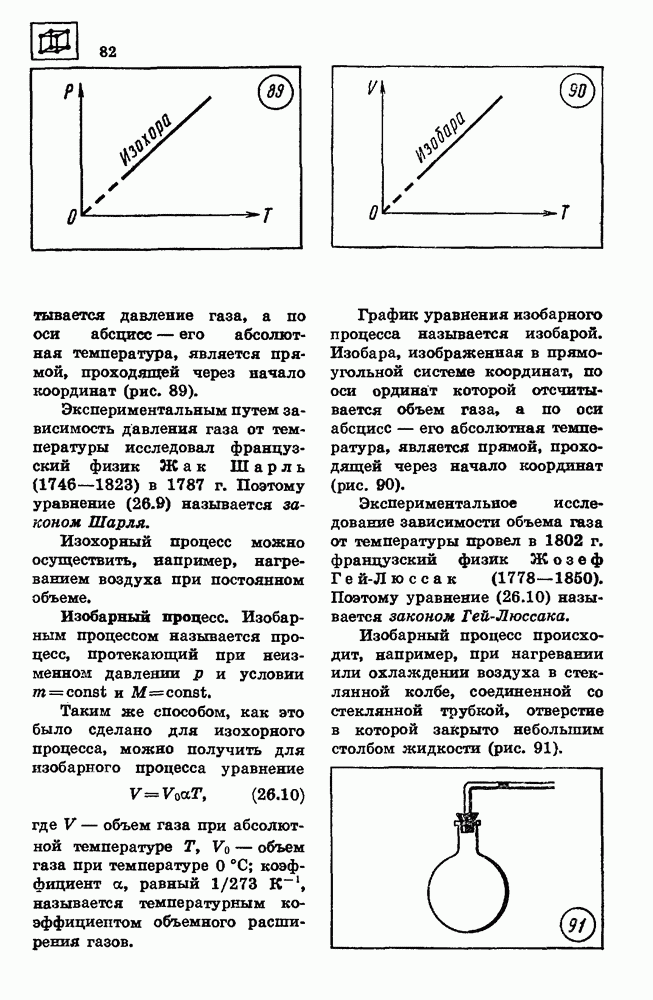
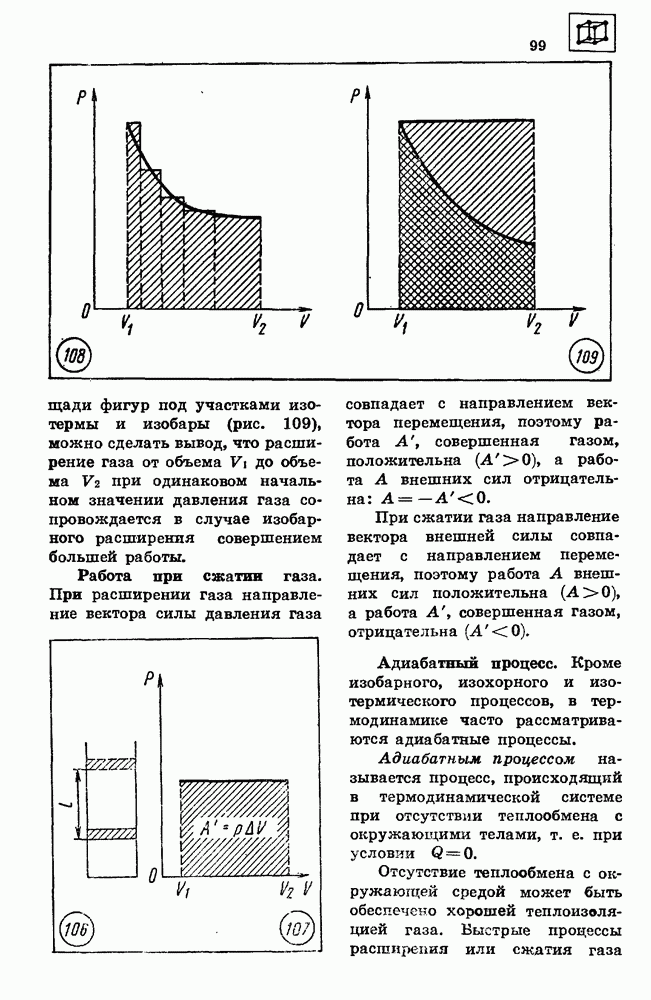
 По графику процесса, осуществленного с идеальным газом (рис. 120), постройте графики этого процесса в координатных осях
По графику процесса, осуществленного с идеальным газом (рис. 120), постройте графики этого процесса в координатных осях  и V, Т. Температура газа в начальном состоянии 1 была равна 250 К.
и V, Т. Температура газа в начальном состоянии 1 была равна 250 К.
Решение
График на рисунке 120 показывает, что давление газа при переходе из состояния 1 в состояние  увеличилось в 3 раза, а объем в течение всего процесса оставался неизменным. Следовательно, процесс изменения состояния газа был изохорным. При изохорном процессе связь между давлением газа
увеличилось в 3 раза, а объем в течение всего процесса оставался неизменным. Следовательно, процесс изменения состояния газа был изохорным. При изохорном процессе связь между давлением газа  и абсолютной температурой Т выражается уравнением
и абсолютной температурой Т выражается уравнением 
Из этого уравнения следует, что отношение давления газа  к абсолютной температуре Т при изохорном процессе является постоянной величиной:
к абсолютной температуре Т при изохорном процессе является постоянной величиной:

Отсюда 
По известным начальным и конечным значениям давления и температуры построим в системе координат с осями  точки 1 и 2, соответствующие начальному и конечному состояниям газа. Зависимость давления
точки 1 и 2, соответствующие начальному и конечному состояниям газа. Зависимость давления  от температуры Т линейная, — следовательно
от температуры Т линейная, — следовательно


график изохорного процесса в координатных осях  является прямой, проходящей через точки 1 и 2 (рис. 121, а).
является прямой, проходящей через точки 1 и 2 (рис. 121, а).
В координатных осях V, Т график изохорного процесса — это отрезок прямой, параллельной оси абсцисс, с ординатой, равной объему газа. Концы отрезка определяются прямыми, параллельными оси ординат и проходящими через точки на оси абсцисс, соответствующие значениям начальной и конечной температуры (рис. 121, б).
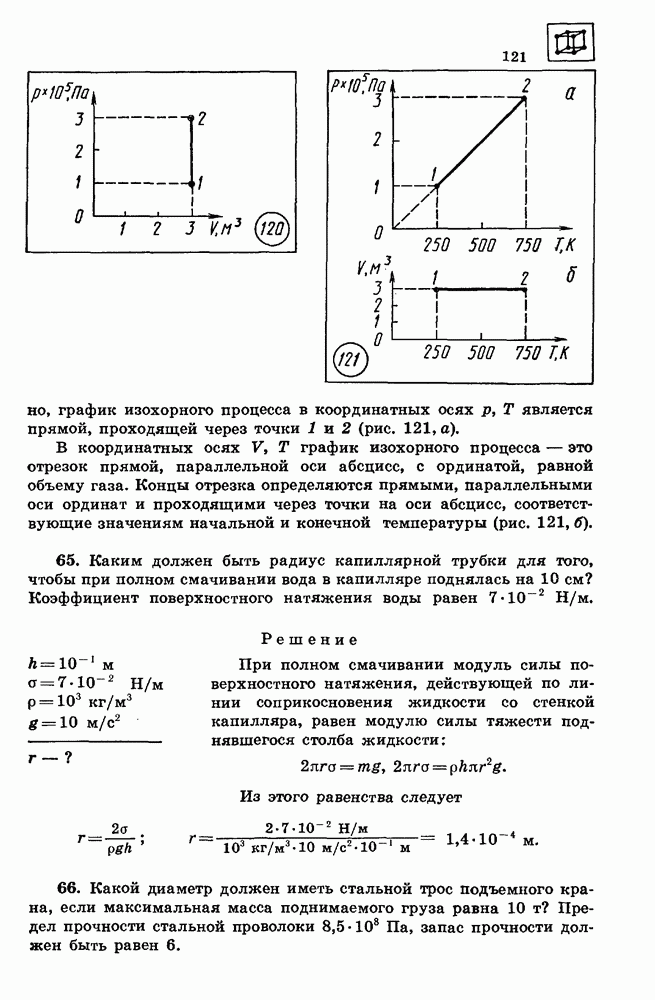
65. Каким должен быть радиус капиллярной трубки для того, чтобы при полном смачивании вода в капилляре поднялась на 10 см? Коэффициент поверхностного натяжения воды равен 

Решение
При полном смачивании модуль силы поверхностного натяжения, действующей по линии соприкосновения жидкости со стенкой капилляра, равен модулю силы тяжести поднявшегося столба жидкости:

Из этого равенства следует

66. Какой диаметр должен иметь стальной трос подъемного крана, если максимальная масса поднимаемого груза равна  Предел прочности стальной проволоки
Предел прочности стальной проволоки  Па, запас прочности должен быть равен 6.
Па, запас прочности должен быть равен 6.

Решение
Предел прочности определяется отношением модуля максимальной силы упругости к площади поперечного сечения:

Так как запас прочности равен 6, трос должен выдерживать нагрузку, в 6 раз превышающую ту, которая возникает при подъеме груза массой 10 т. Следовательно,

Отсюда диаметр троса равен

67. Вычислите работу совершаемую одним молем идеального газа при изобарном нагревании на 1 К.

Решение
При изобарном нагревании идеального газа работа А, совершаемая газом, равна

Так как по условию задачи не даны значения давления  газа и изменения его объема
газа и изменения его объема  выразим эти величины через известное изменение
выразим эти величины через известное изменение  температуры газа. Для этого воспользуемся уравнением состояния идеального газа
температуры газа. Для этого воспользуемся уравнением состояния идеального газа

Из этих уравнений получаем

Отсюда для работы газа при изобарном нагревании будем иметь

Дне.
Таким образом, молярная газовая постоянная  равна работе, совершаемой одним молем идеального газа при изобарном нагревании на 1 К.
равна работе, совершаемой одним молем идеального газа при изобарном нагревании на 1 К.
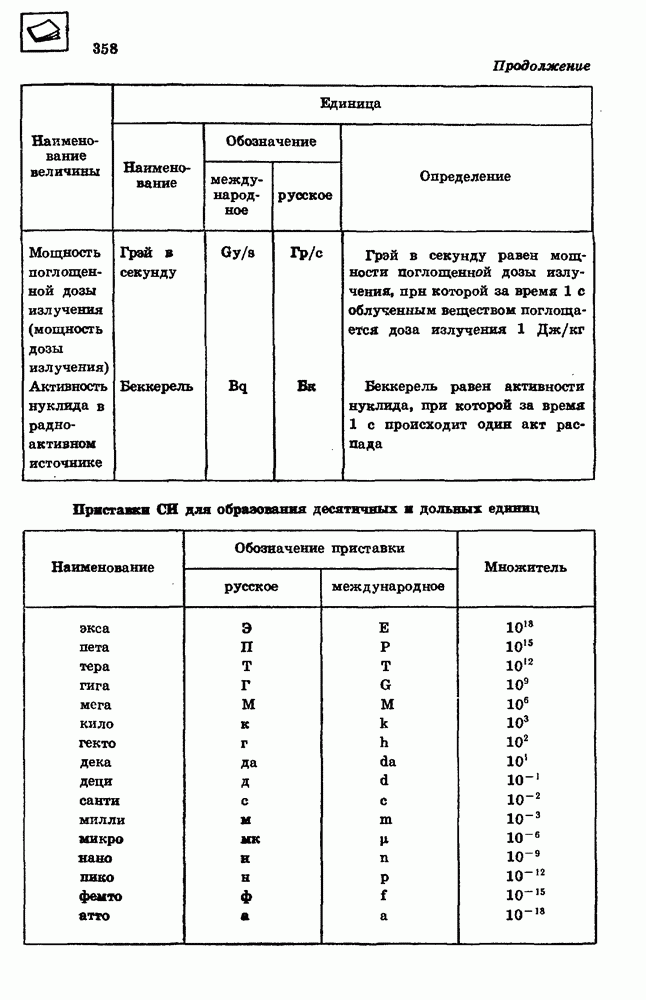
68. Определите максимальный КПД тепловой машины, если температура нагревателя равна 227 °С, а температура холодильника — 27 °С.

Решение
Максимальный КПД тепловой машины определяется выражением

69. Карбюраторный двигатель внутреннего сгорания работает по циклу, состоящему из четырех последовательно происходящих процессов: адиабатного сжатия из состояния А в состояние В, изохорного перехода из состояния В в состояние С в результате нагревания воздуха при сжигании горючей смеси, адиабатного расширения из состояния С в состояние  и изохорного перехода из состояния
и изохорного перехода из состояния  в исходное состояние А (см. рис. 117). Вычислите КПД двигателя для случая, если бы воздух был идеальным: одиоатомным газом при значениях температуры в состояниях А, В, С и D соответственно
в исходное состояние А (см. рис. 117). Вычислите КПД двигателя для случая, если бы воздух был идеальным: одиоатомным газом при значениях температуры в состояниях А, В, С и D соответственно 
Решение
Значение КПД теплового двигателя определяется уравнением

где  — количество теплоты, переданное за цикл рабочему телу от нагревателя;
— количество теплоты, переданное за цикл рабочему телу от нагревателя;  — количество теплоты, полученное за цикл холодильником от рабочего тела.
— количество теплоты, полученное за цикл холодильником от рабочего тела.
Во время осуществления адиабатических процессов расширения и сжатия нет теплообмена рабочего тела ни с холодильником, ни с нагревателем. Следовательно, весь процесс теплоотдачи количества теплоты  от нагревателя осуществляется при переходе газа из состояния В в состояние С, а процесс передачи количества теплоты
от нагревателя осуществляется при переходе газа из состояния В в состояние С, а процесс передачи количества теплоты  холодильнику — при переходе газа из состояния
холодильнику — при переходе газа из состояния  в состояние А. При изохорическом переходе газа из состояния В в состояние С работа внешних
в состояние А. При изохорическом переходе газа из состояния В в состояние С работа внешних  равна нулю:
равна нулю:  так как поршень неподвижен. Из первого закона термодинамики для этого процесса следует
так как поршень неподвижен. Из первого закона термодинамики для этого процесса следует

Мы получили, что количество теплоты, полученное газом от нагревателя за весь цикл, равно изменению внутренней энергии газа при переходе из состояния В в состояние С:

Аналогично количество теплоты  переданное холодильнику при изохорическом переходе газа из состояния
переданное холодильнику при изохорическом переходе газа из состояния  в состояние А, равно
в состояние А, равно

Подставляя полученные выражения для  в уравнение для определения КПД, получаем
в уравнение для определения КПД, получаем

Найдем численное значение 

70. В теплоизолированном сосуде находятся вода и лед при температуре  Массы воды и льда соответственно равны 0,5 кг и
Массы воды и льда соответственно равны 0,5 кг и  В воду впускается водяной пар массой
В воду впускается водяной пар массой  при температуре
при температуре  Какой станет температура воды в сосуде после установления теплового равновесия? Теплоемкость сосуда в расчетах не учитывать.
Какой станет температура воды в сосуде после установления теплового равновесия? Теплоемкость сосуда в расчетах не учитывать.

Решение
Проверим сначала, достаточно ли выделяющегося при конденсации пара количества теплоты  для плавления льда.
для плавления льда.
При конденсации пара выделяется количество теплоты 

Для плавления льда требуется количество теплоты 

Сравнение количеств теплоты  показывает, что
показывает, что  поэтому уравнение теплового баланса имеет вид
поэтому уравнение теплового баланса имеет вид

Теплота выделяется при конденсации пара массой  и остывании сконденсировавшейся воды от температуры
и остывании сконденсировавшейся воды от температуры  до некоторого значения
до некоторого значения  а поглощается при плавлении льда массой
а поглощается при плавлении льда массой  и нагревании воды массой
и нагревании воды массой  от температуры
от температуры  до равновесного значения
до равновесного значения  Обозначив
Обозначив  для разности
для разности  получим
получим

Уравнение теплового баланса приобретает вид

Откуда

Тогда 
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
(см. скан)
(см. скан)
ЭЛЕКТРОДИНАМИКА
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
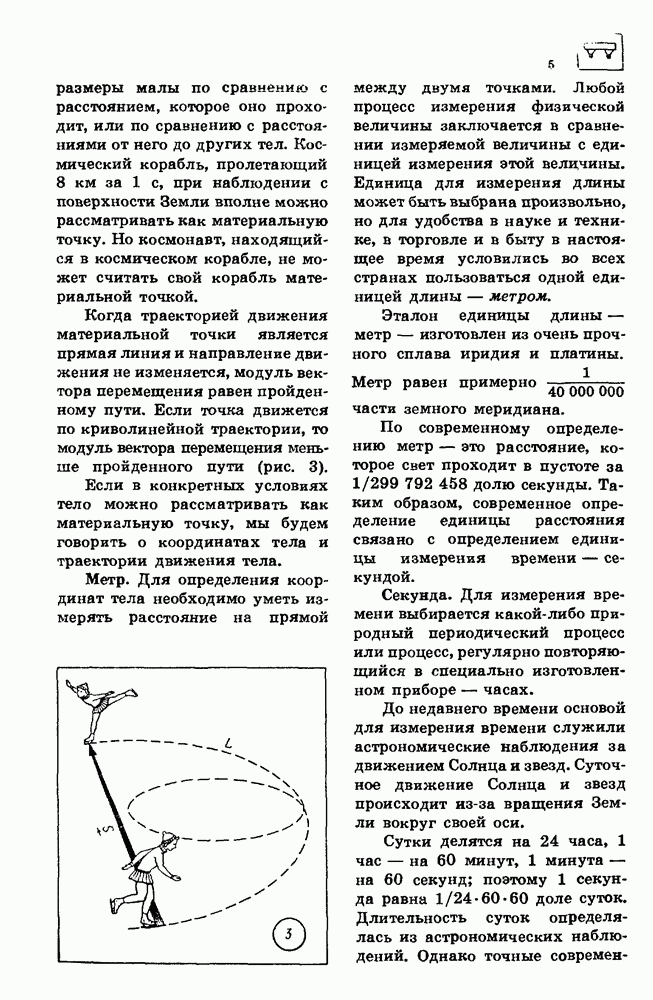
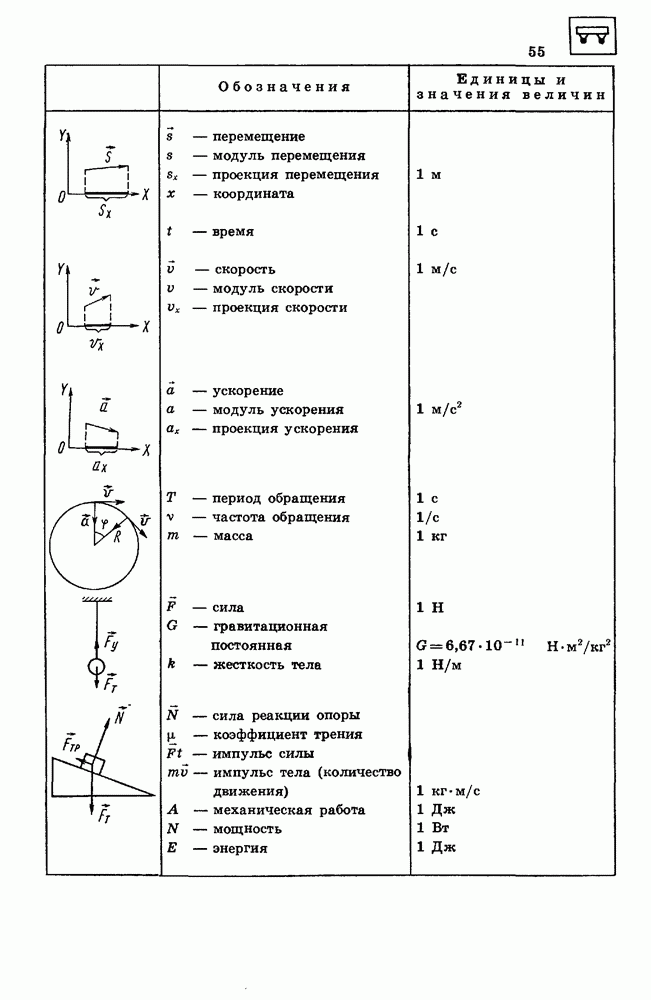
- 1. МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ
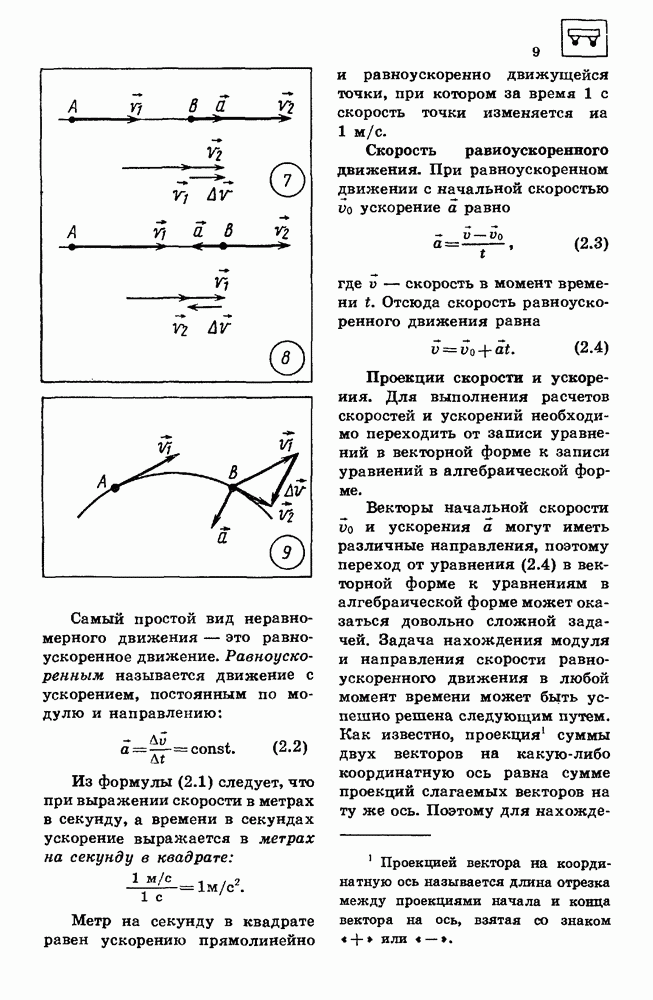
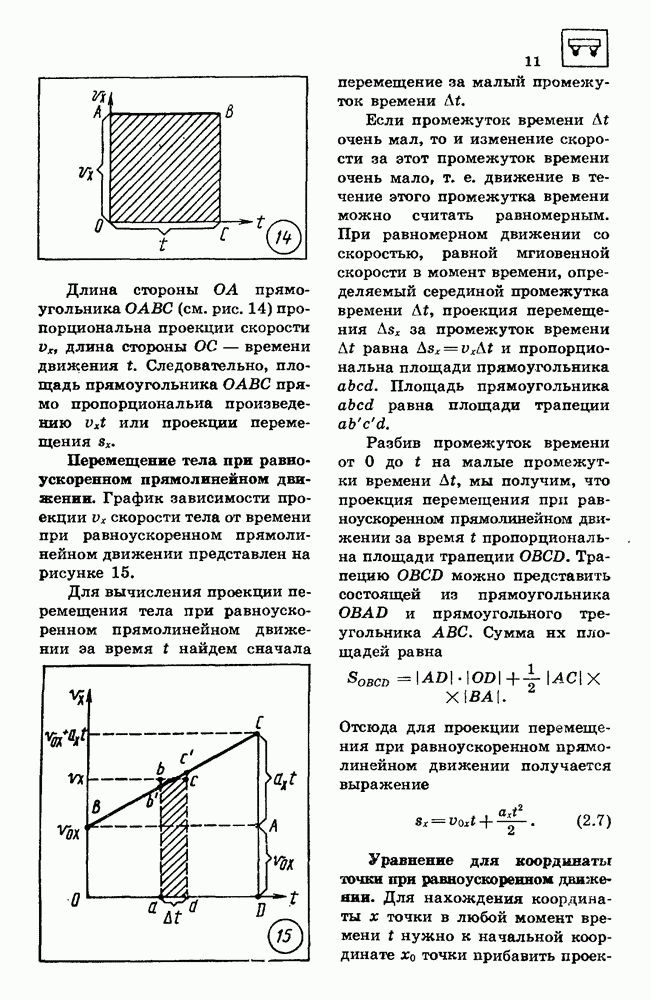
- 2. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- 3. РАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
- 4. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- 5. МАССА ТЕЛА
- 6. СИЛА
- 7. ВТОРОЙ ЗАКОН НЬЮТОНА
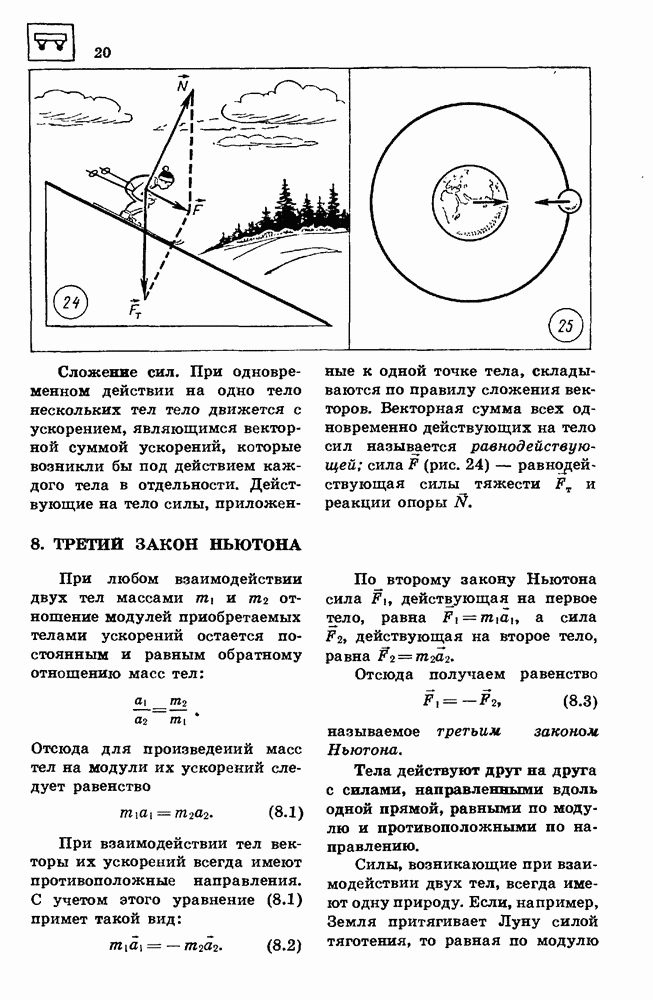
- 8. ТРЕТИЙ ЗАКОН НЬЮТОНА
- 9. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
- 10. ВЕС И НЕВЕСОМОСТЬ
- 11. ДВИЖЕНИЕ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- 12. СИЛА УПРУГОСТИ
- 13. СИЛЫ ТРЕНИЯ
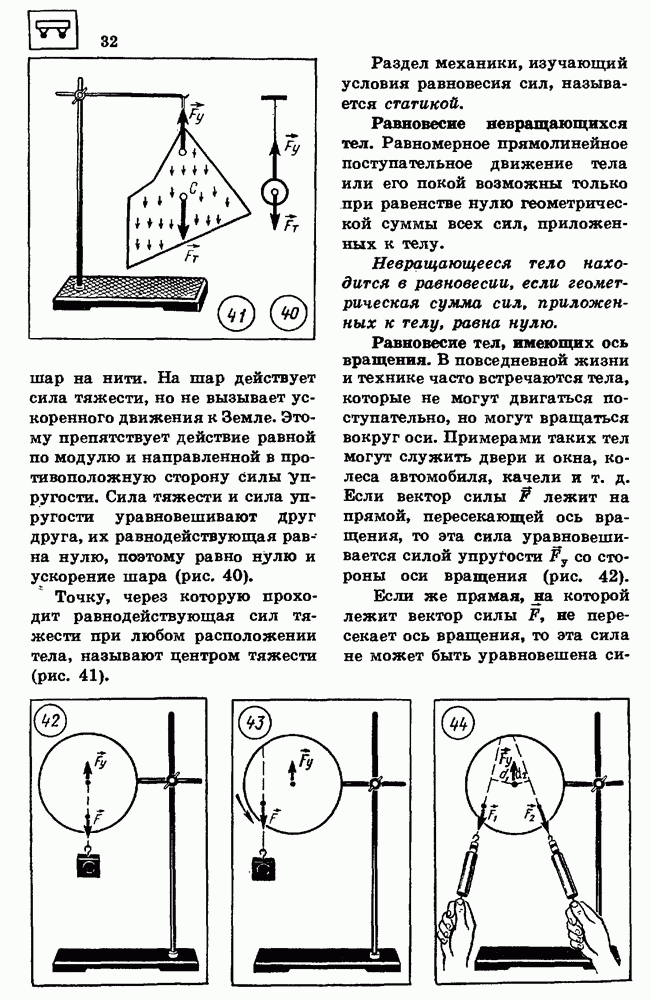
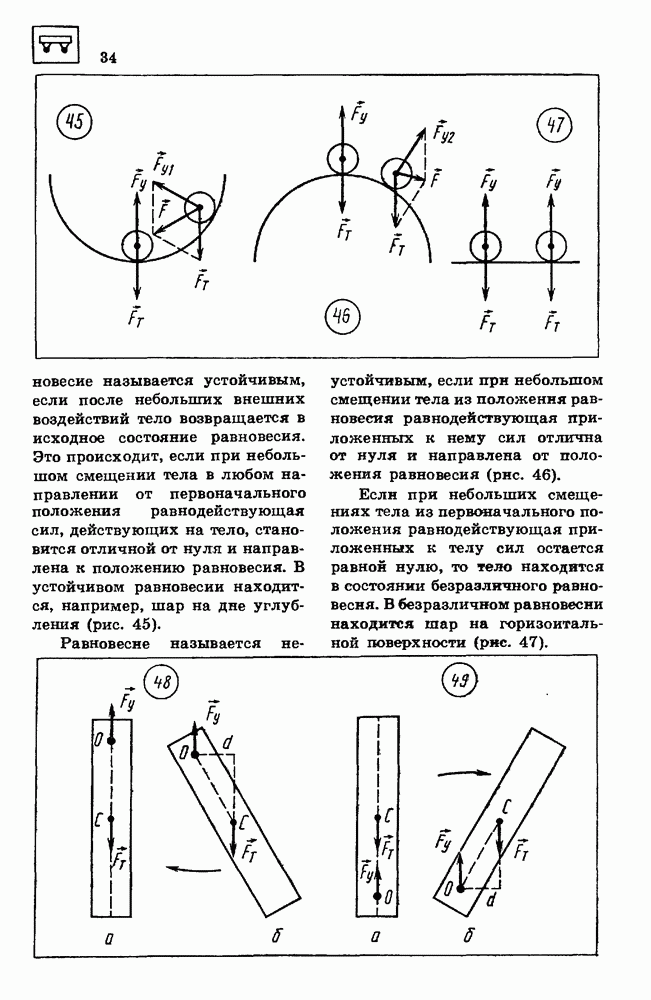
- 14. УСЛОВИЯ РАВНОВЕСИЯ ТЕЛ
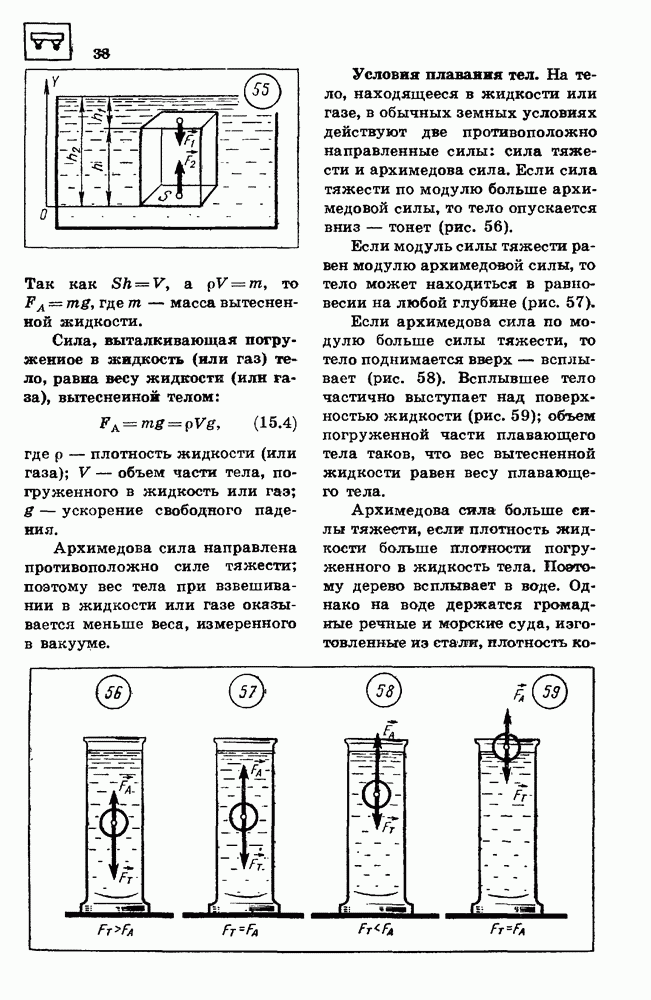
- 15. ЭЛЕМЕНТЫ ГИДРОСТАТИКИ
- 16. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- 17. РЕАКТИВНОЕ ДВИЖЕНИЕ
- 18. МЕХАНИЧЕСКАЯ РАБОТА
- 19. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- 20. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
- 21. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ В МЕХАНИЧЕСКИХ ПРОЦЕССАХ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 22. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОИ ТЕОРИИ И ИХ ОПЫТНОЕ ОБОСНОВАНИЕ
- 23. МАССА МОЛЕКУЛ
- 24. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОИ ТЕОРИИ ИДЕАЛЬНОГО ГАЗА
- 25. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- 28. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- 27. СВОЙСТВА ЖИДКОСТЕЙ
- 28. ИСПАРЕНИЕ И КОНДЕНСАЦИЯ
- 29. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА
- 30. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ЦЕЛ
- 31. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 32. КОЛИЧЕСТВО ТЕПЛОТЫ
- 33. РАБОТА ПРИ ИЗМЕНЕНИИ ОБЪЕМА ГАЗА
- 34. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДБИГАТЕЛЕЙ
- 35. ТЕПЛОВЫЕ МАШИНЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 36. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- 37. ЗАКОН КУЛОНА
- 38. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 39. РАБОТА ПРИ ПЕРЕМЕЩЕНИИ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- 40. ПОТЕНЦИАЛ
- 41. ВЕЩЕСТВО В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- 42. ЭЛЕКТРОЕМКОСТЬ
- 43. ЗАКОН ОМА
- 44. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ
- 45. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- 46. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ
- 47. ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
- 48. ОТКРЫТИЕ ЭЛЕКТРОНА
- 49. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ
- 50. ЭЛЕКТРИЧЕСКИИ ТОК В ВАКУУМЕ
- 51. МАГНИТНОЕ ПОЛЕ
- 52. СИЛА ЛОРЕНЦА
- 53. ВЕЩЕСТВО В МАГНИТНОМ ПОЛЕ
- 54. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- 55. САМОИНДУКЦИЯ
- 56. МАГНИТНАЯ ЗАПИСЬ ИНФОРМАЦИИ
- 57. МАШИНА ПОСТОЯННОГО ТОКА
- 58. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 59. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
- 60. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
- 61. ПРЕВРАЩЕНИЯ ЭНЕРГИИ ПРИ МЕХАНИЧЕСКИХ КОЛЕБАНИЯХ
- 62. РАСПРОСТРАНЕНИЕ КОЛЕБАНИИ В УПРУГОЙ СРЕДЕ
- 63. ЗВУКОВЫЕ ВОЛНЫ
- 64. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ВОЛН
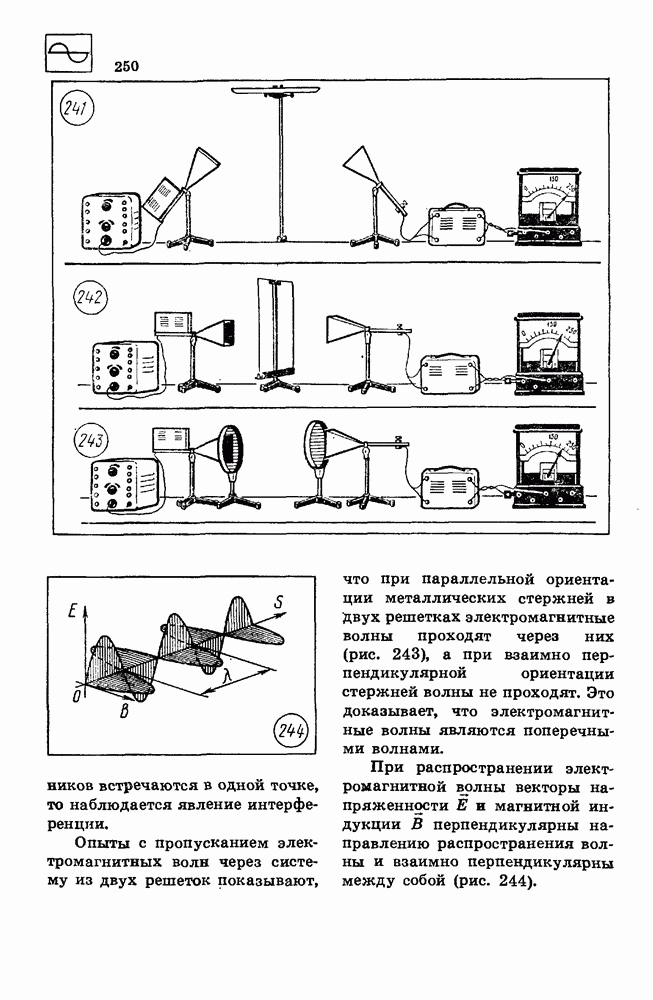
- 65. ИНТЕРФЕРЕНЦИЯ, ДИФРАКЦИЯ И ПОЛЯРИЗАЦИЯ ВОЛН
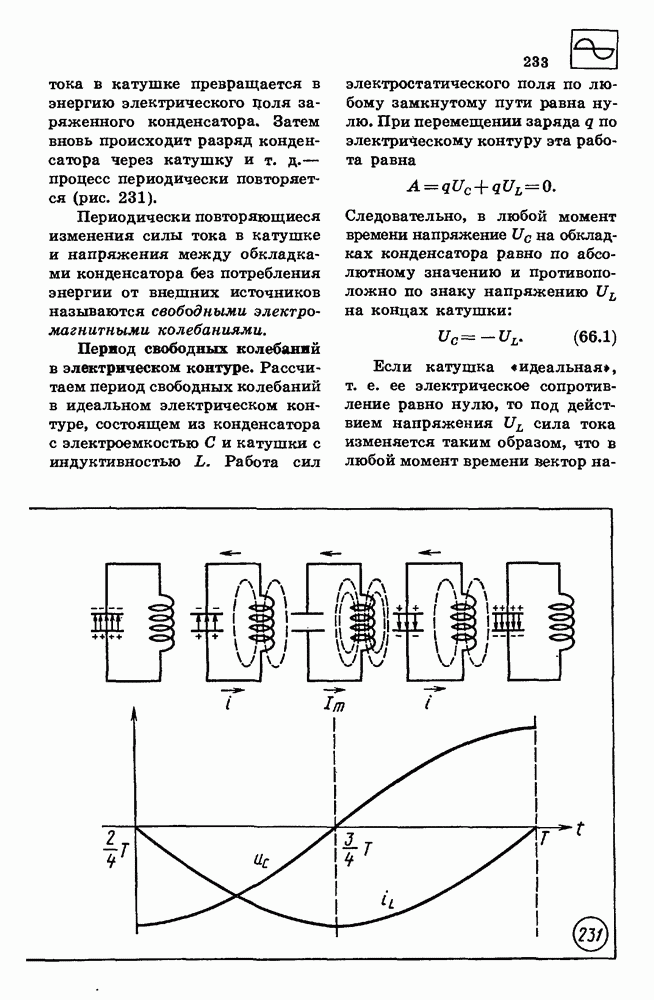
- 66. СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
- 67. АВТОКОЛЕБАТЕЛЬНЫЙ ГЕНЕРАТОР НЕЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИИ
- 68. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- 69. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 70. ИНДУКТИВНОСТЬ И ЕМКОСТЬ В ЦКТТИ ПЕРЕМЕННОГО ТОКА
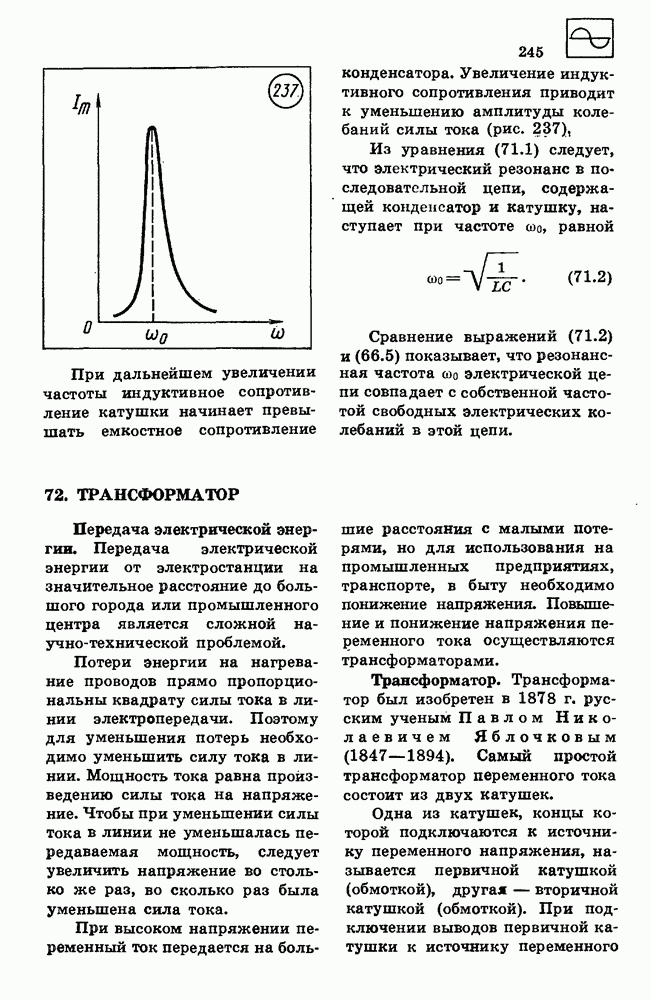
- 71. РЕЗОНАНС В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
- 72. ТРАНСФОРМАТОР
- 73. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
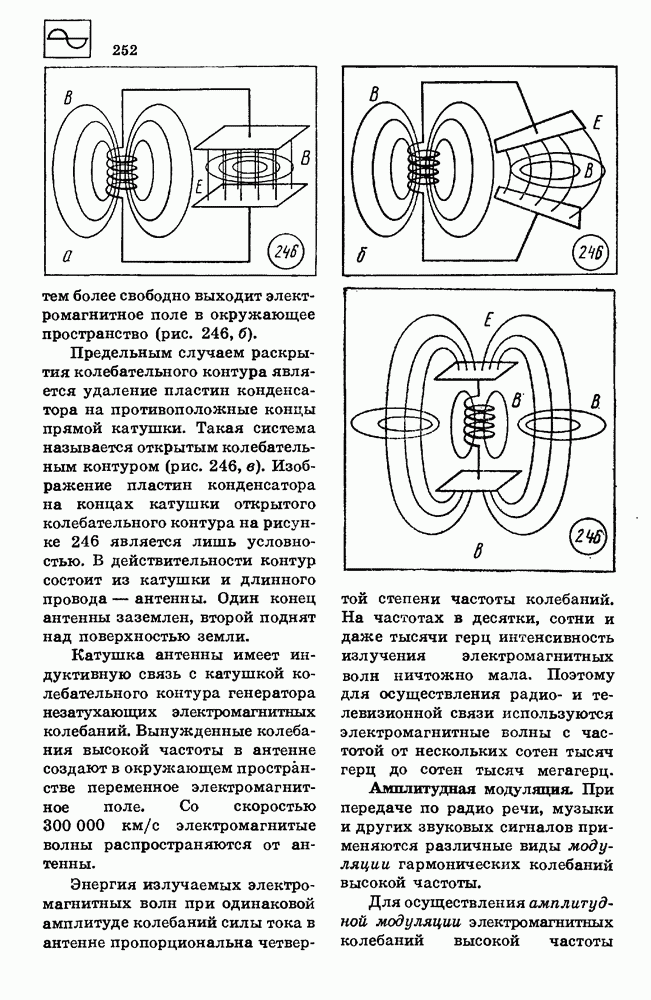
- 74. ПРИНЦИПЫ РАДИОСВЯЗИ
- 75. ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 76. РАЗВИТОЕ ПРЕДСТАВЛЕНИИ О ПРИРОДЕ СВЕТА
- 77. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
- 78. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 79. ОПТИЧЕСКИЕ ПРИБОРЫ
- 80. СПЕКТР ЭЛЕКТРОМАГНИТНЫХ ИЗЛУЧЕНИЙ
- 81. ЭЛЕМЕНТЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
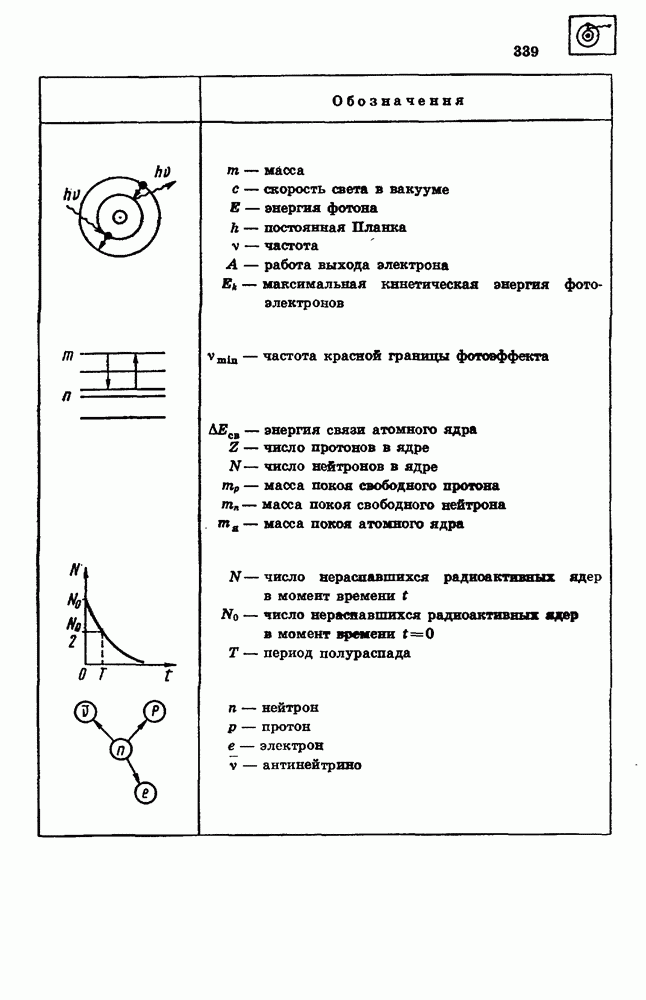
- 82. КВАНТОВЫЕ СВОЙСТВА СВЕТА
- 83. ДОКАЗАТЕЛЬСТВА СЛОЖНОЙ СТРУКТУРЫ АТОМОВ
- 84. КВАНТОВЫЕ ПОСТУЛАТЫ БОРА
- 86. АТОМНОЕ ЯДРО
- 87. РАДИОАКТИВНОСТЬ
- 88. СВОЙСТВА ЯДЕРНЫХ ИЗЛУЧЕНИЙ
- 89. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ РЕГИСТРАЦИИ ЗАРЯЖЕННЫХ ЧАСТИЦ
- 90. ЦЕПНАЯ РЕАКЦИЯ ДЕЛЕНИЯ ЯДЕР УРАНА
- 91. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- ПРИЛОЖЕНИЯ