| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Связь между значениями и их рангами
Если становится известным значение ранга  то элемент выборки
то элемент выборки  при этом условии становится
при этом условии становится  порядковой статистикой
порядковой статистикой  с распределением
с распределением

что совпадает с ранее полученным (5).
Рассмотрим некоторые количественные характеристики атой связи.
Выясним сначала, как ведут себя линии регрессии — условные математические ожидания значений и рангов. Они определяются уравнениями

и

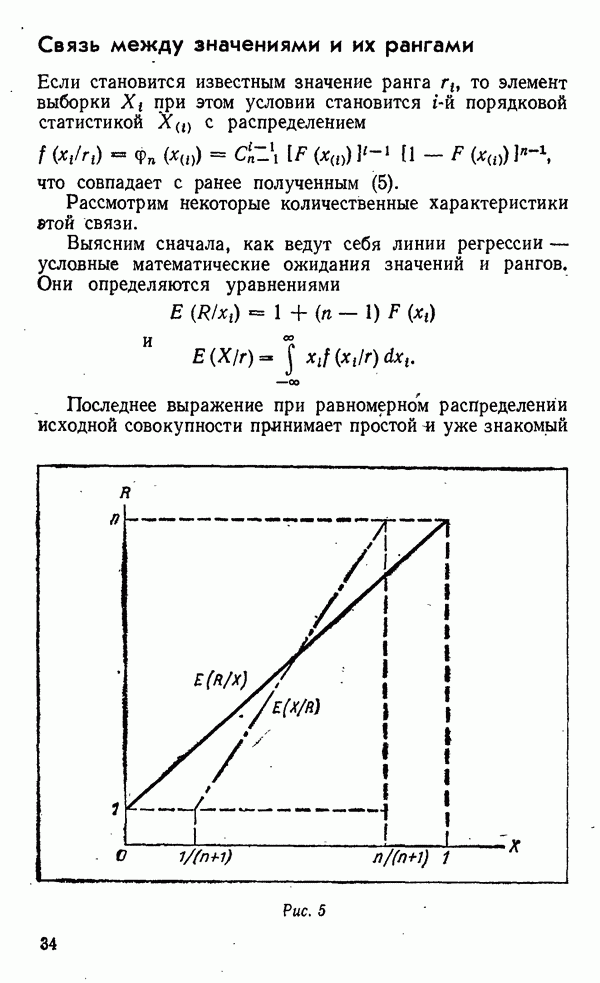
Последнее выражение при равномерном распределении исходной совокупности принимает простой и уже знакомый

Рис. 5
нам вид:  Это не что иное, как среднее
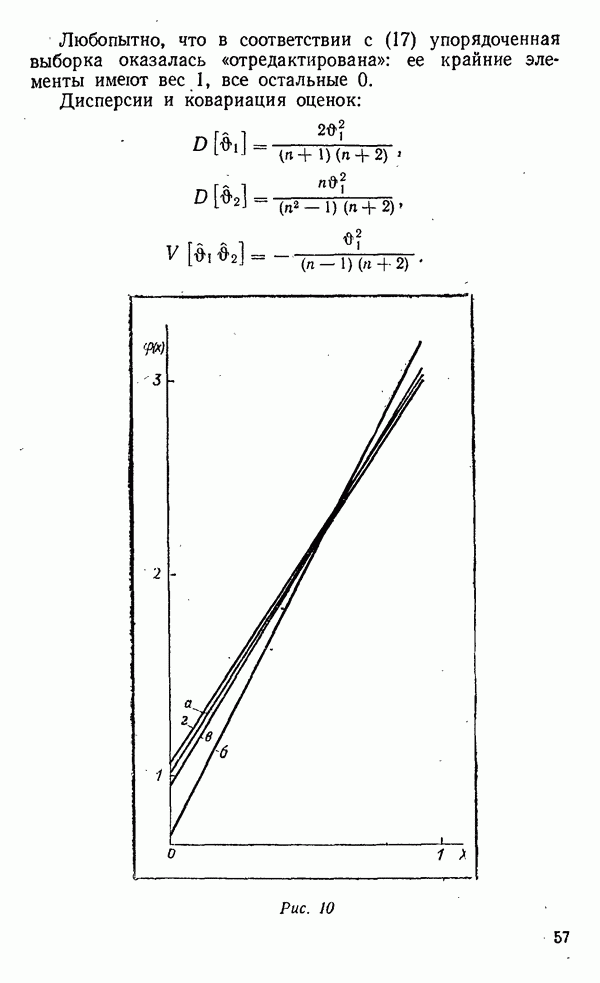
Это не что иное, как среднее  порядковой статистики. Нанесем обе линии регрессии на один график (рис. 5). Они не совпадают, а ведь именно совпадение линий регрессии говорит, как известно, о функциональной зависимости между случайными величинами, образующими систему. Однако они и не перпендикулярны, что свидетельствовало бы о Некоррелированности величин
порядковой статистики. Нанесем обе линии регрессии на один график (рис. 5). Они не совпадают, а ведь именно совпадение линий регрессии говорит, как известно, о функциональной зависимости между случайными величинами, образующими систему. Однако они и не перпендикулярны, что свидетельствовало бы о Некоррелированности величин 
Обратим внимание на то обстоятельство, что с увеличением объема выборки  угол между линиями неограниченно убывает, что говорит об усилении связи. Статистическая зависимость приближается к зависимости функциональной. Другая мера статистической связи — коэффициент корреляции, естественно, имеет ту же тенденцию — возрастать с увеличением
угол между линиями неограниченно убывает, что говорит об усилении связи. Статистическая зависимость приближается к зависимости функциональной. Другая мера статистической связи — коэффициент корреляции, естественно, имеет ту же тенденцию — возрастать с увеличением  но кроме того, он демонстрирует еще одно важное свойство зависимости между
но кроме того, он демонстрирует еще одно важное свойство зависимости между 
Коэффициент корреляции между  по определению равен
по определению равен

Преобразование этого выражения с учетом того, что распределение  равномерно, приводит к
равномерно, приводит к

Произошла факторизация коэффициента корреляции. Один сомножитель зависит только от объема выборки и стремится к единице при  второй же определяется лишь видом исходного распределения
второй же определяется лишь видом исходного распределения  Замечательно то, что конструкция зависимости
Замечательно то, что конструкция зависимости  такова, что выполняется следующее равенство при любых а и а;
такова, что выполняется следующее равенство при любых а и а;

Это значит, что коэффициент корреляции между значением и рангом не зависит от параметров расположения и рассеяния этих случайных величин. Интуитивно это понятно. Действительно, «сдвинем» ранги, т. е. пронумеруем элементы выборки при  не от 1 до 10, а от 11 до 20. Очевидно связь между значениями и их местами в ряду останется прежней. Выясним еще одно свойство связи между величинами
не от 1 до 10, а от 11 до 20. Очевидно связь между значениями и их местами в ряду останется прежней. Выясним еще одно свойство связи между величинами  вычислив количество информации,
вычислив количество информации,
которое они несут друг о друге. Преобразование общего выражения

где  вероятность ранга
вероятность ранга  приводит при
приводит при  к асимптотической формуле
к асимптотической формуле

Нетрудно видеть, что при неограниченном возрастании выборки количество информации в  о X (и наоборот) также неограниченно растет, причем принимает одинаковые значения для всех непрерывных распределений, поскольку
о X (и наоборот) также неограниченно растет, причем принимает одинаковые значения для всех непрерывных распределений, поскольку  в (8) не входит.
в (8) не входит.
Суммируем результаты. Итак, ранги и выборочные значения статистически связаны. С ростом объема выборки эта связь становится жестче, асимптотически переходя в однозначную функциональную зависимость, при которой одна величина полностью определяет другую. Зависимость между выборочными значениями и рангами не только не меняется, с параметрами сдвига и масштаба, но и свободна (при больших  от вида распределения исходной, совокупности.
от вида распределения исходной, совокупности.
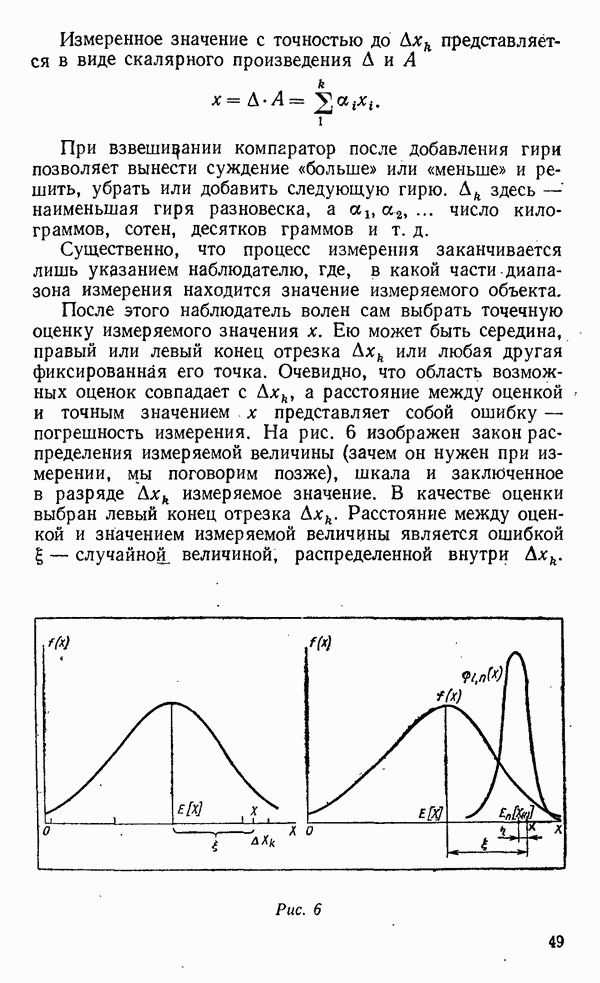
С выяснением этих свойств немедленно возникает вопрос: как можно и где нужно их использовать? Сейчас мы посмотрим, как можно пользоваться обнаруженной связью, а область применения ранговых процедур выясним позже.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
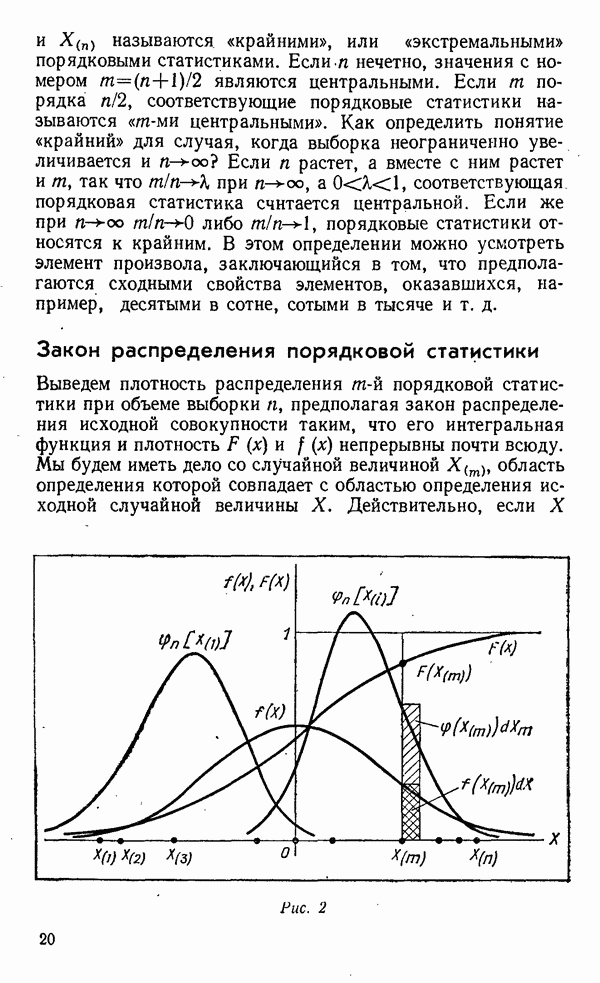
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
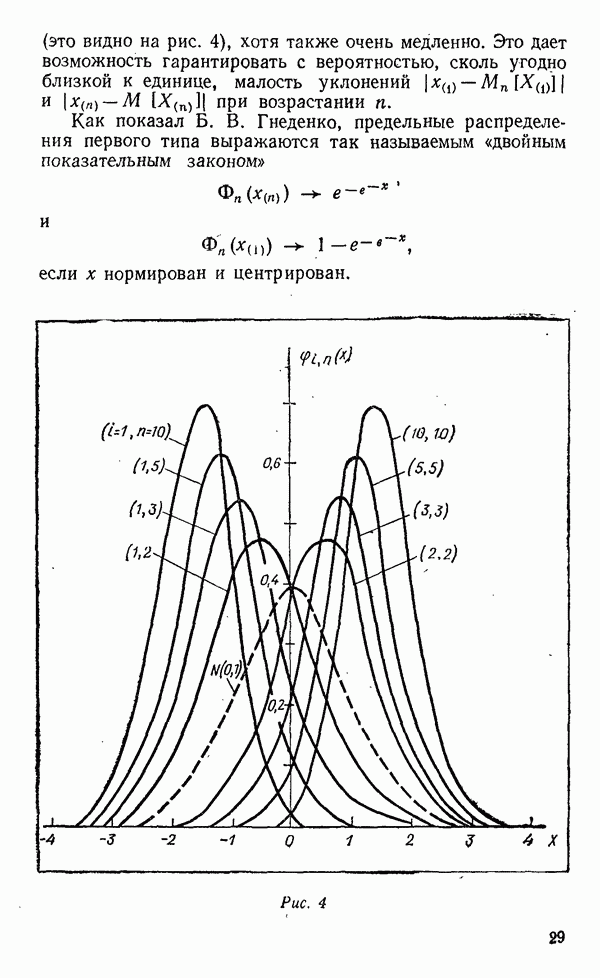
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
- Идентификация объекта с ненаблюдаемым входом
- Безэталонная классификация
- ЛИТЕРАТУРА