| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Оценки параметров нормального распределения по усеченным выборкам
Оценивание параметров нормального распределения по малым усеченным выборкам сочетает высокую эффективность и простоту вычислений. Будем рассматривать выборки, усеченные с двух сторон — на  наименьших и
наименьших и  наибольших членов. Для них оценки математического ожидания и среднеквадратического отклонения вычисляются по формулам:
наибольших членов. Для них оценки математического ожидания и среднеквадратического отклонения вычисляются по формулам:

и

Весовые коэффициенты  определяются из выражений:
определяются из выражений:

и

где  математическое ожидание нормированной 1-й порядковой статистики, а
математическое ожидание нормированной 1-й порядковой статистики, а

— среднее неусеченных.
Таким путем получаются несмещенные оценки 2: и а не только при несимметричном, но даже н при одностороннем усечении выборки, когда  или
или 
Для получения оценок (15) и (16) достаточно, как мы видим, знать только математическое ожидание порядковых статистик.
Коэффициенты  растут от края ранжированной выборки к медианному (центральному) значению, которое и получает наибольший вес.
растут от края ранжированной выборки к медианному (центральному) значению, которое и получает наибольший вес.
Эффективность оценки  сравнивается с эффективностью оптимальной оценки и оказывается, как уже отмечалось, хуже. Проследим, как изменяется эффективность по мере отбрасывания крайних членов. Оказывается, что оценка
сравнивается с эффективностью оптимальной оценки и оказывается, как уже отмечалось, хуже. Проследим, как изменяется эффективность по мере отбрасывания крайних членов. Оказывается, что оценка  мало чувствительна к присутствию крайних (их вес мал).
мало чувствительна к присутствию крайних (их вес мал).
Так, если отброшены крайние и оценкой служит просто среднее из оставшихся (даже без вычисления  ее
ее
эффективность может достигнуть  Если количество элементов в выборке
Если количество элементов в выборке  и усечены все
и усечены все  ее элементы, кроме центрального и соседнего с ним, оценкой
ее элементы, кроме центрального и соседнего с ним, оценкой  служит центральное значение, соседнее можно не учитывать вовсе, а эффективность при этом составляет более
служит центральное значение, соседнее можно не учитывать вовсе, а эффективность при этом составляет более  Например, если при
Например, если при  оставлены всего два наблюдения
оставлены всего два наблюдения  а остальные усечены, эффективность оценки остается равной 72 %. Но стоит потерять хотя бы одно из этих центральных наблюдений
а остальные усечены, эффективность оценки остается равной 72 %. Но стоит потерять хотя бы одно из этих центральных наблюдений  например), как эффективность падает за 60 %, даже если, с другой стороны, добавить все недостающие до полной выборки наблюдения.
например), как эффективность падает за 60 %, даже если, с другой стороны, добавить все недостающие до полной выборки наблюдения.
Для оценки математического ожидания, таким образом, одно центральное наблюдение значит больше, чем половина выборки.
Оценка среднеквадратичного отклонения о ведет себя в этом смысле по-другому: при любом фиксированном  эффективность убывает на одну и ту же величину при каждом шаге уменьшения
эффективность убывает на одну и ту же величину при каждом шаге уменьшения  Здесь усечения следует производить осторожно. Так, если при
Здесь усечения следует производить осторожно. Так, если при  отбрасывать два наблюдения с одного края или по одному с противоположных, эффективность снижается до
отбрасывать два наблюдения с одного края или по одному с противоположных, эффективность снижается до  Отбрасывание третьего наблюдения (практически любого) снижает ее до
Отбрасывание третьего наблюдения (практически любого) снижает ее до  а каждого «последующего — еще на 3 %.
а каждого «последующего — еще на 3 %.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
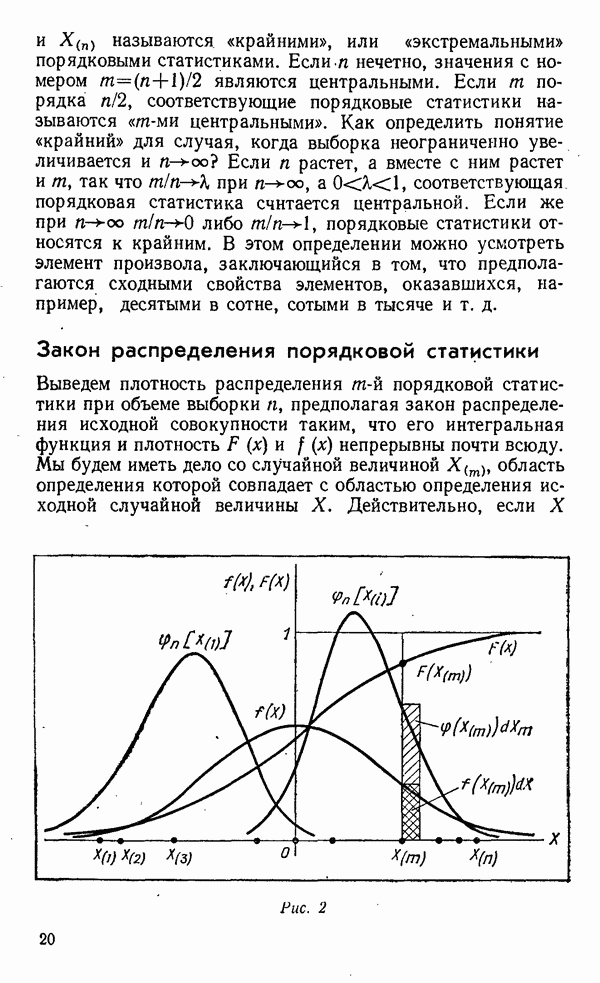
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
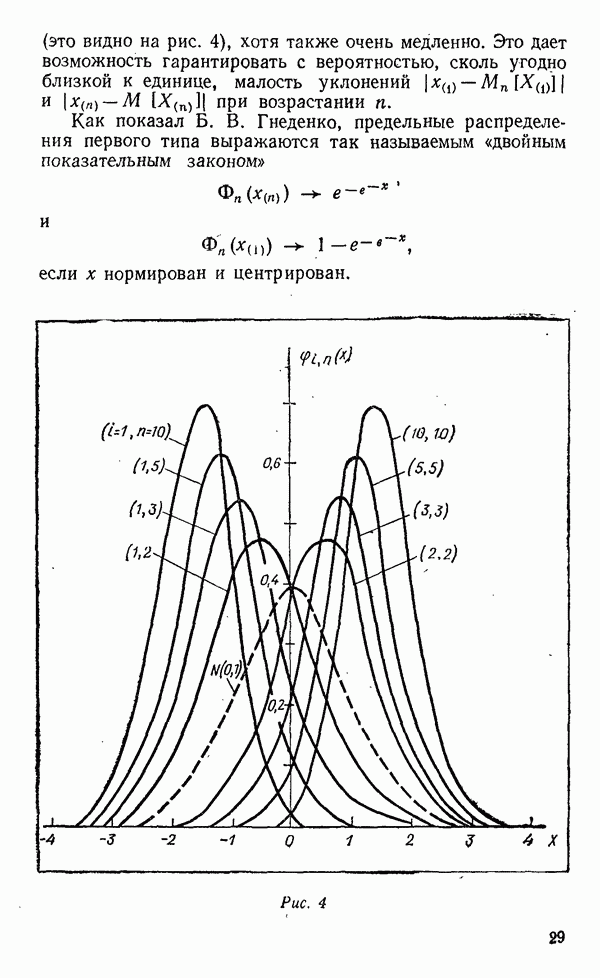
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
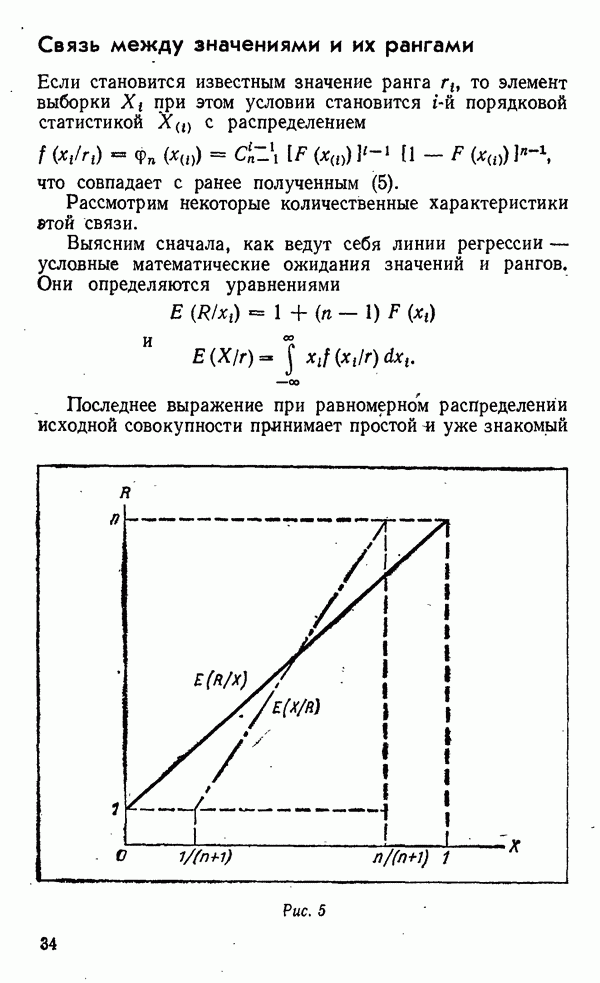
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
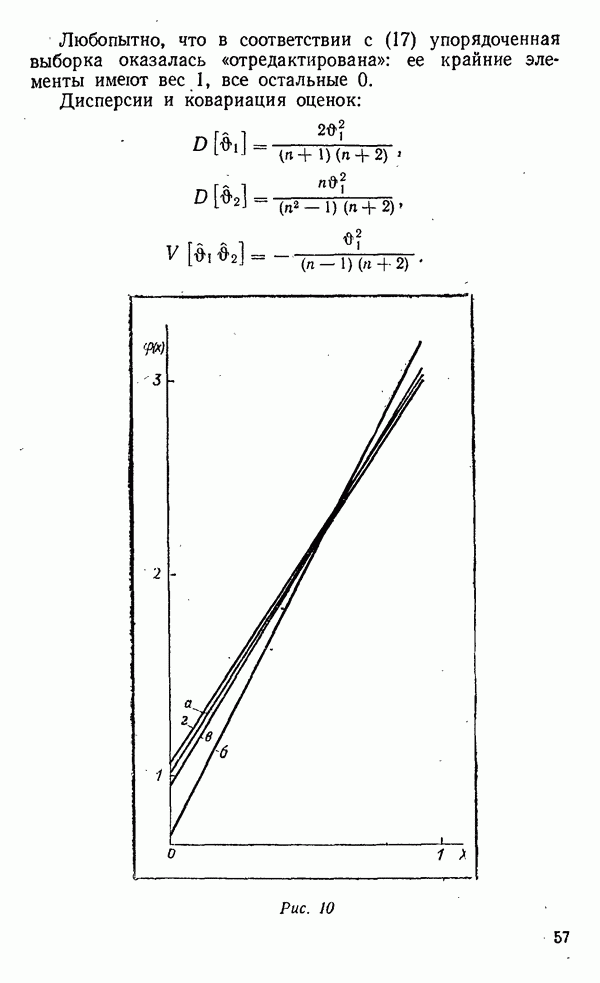
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
- Идентификация объекта с ненаблюдаемым входом
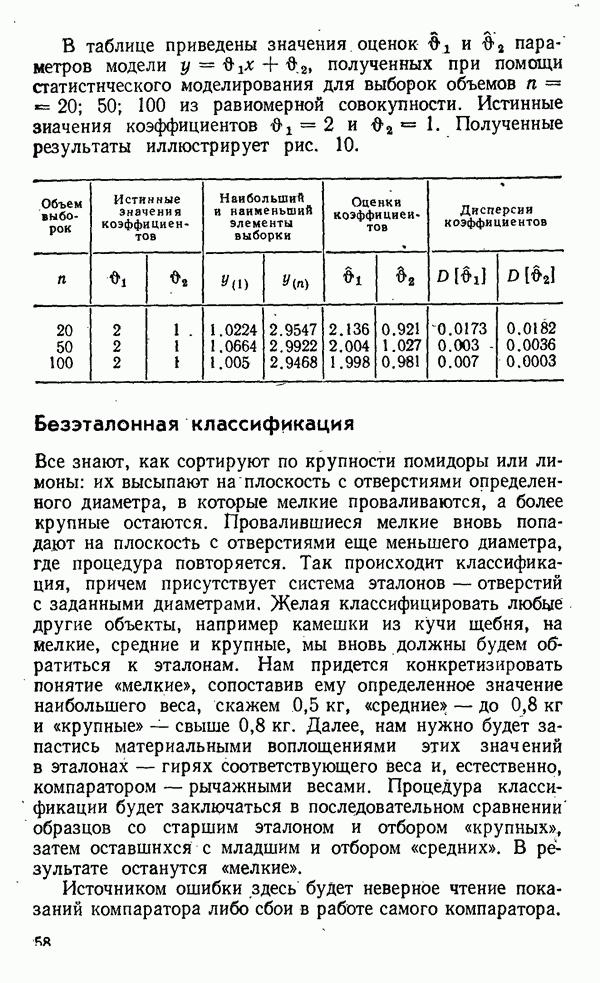
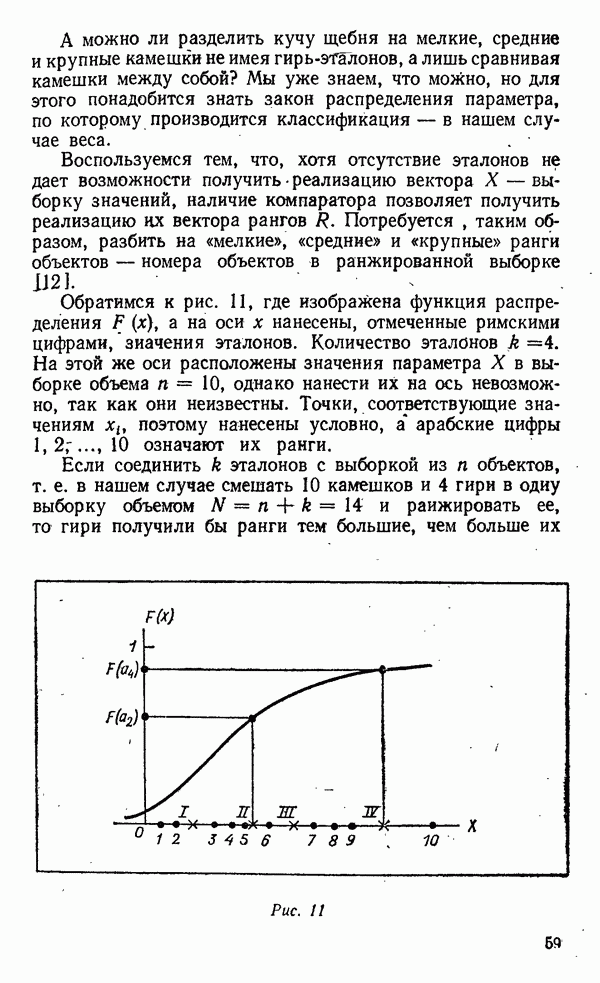
- Безэталонная классификация
- ЛИТЕРАТУРА