| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Ранжированная выборка — объект с новыми свойствами
Почему выборка из X — вероятностный объект? Да потому, возникает естественный ответ, что ее элементы имеют случайные значения, подчиненные определенному закону распределения. Но не только по этой причине. Заинтересовавшись вопросами сортировки, выделения крайних, средних, да и вообще любых номеров, которые получают элементы при любом упорядочении выборки, мы немедленно столкнемся с новыми вероятностными свойствами ее элементов.
Действительно, выборка, содержащая одни и те же элементы, может быть реализована в опыте  разными способами в зависимости от порядка следования элементов. Если опыт поставлен правильно, все возможные реализации равновероятны и среди них с вероятностью
разными способами в зависимости от порядка следования элементов. Если опыт поставлен правильно, все возможные реализации равновероятны и среди них с вероятностью  может оказаться выборка, ранжированная уже в процессе формирования. Напомним, что вероятность эта очень мала даже для небольших объемов выборки. При
может оказаться выборка, ранжированная уже в процессе формирования. Напомним, что вероятность эта очень мала даже для небольших объемов выборки. При  она равна 0,00000000208 и, если на одну выборку уходит 1 с, требуемую реализацию можно ждать в течение нескольких
она равна 0,00000000208 и, если на одну выборку уходит 1 с, требуемую реализацию можно ждать в течение нескольких
тысяч лет. Мы приводим этот пример для того, чтобы подчеркнуть, что операция упорядочения превращает ранжированную выборку в уникальный объект, настолько же редкий среди «естественных» реализаций, как может быть редок осмысленный текст среди случайных последовательностей букв.
Отличие ранжированной выборки от исходной, «естественной», количественно можно оценить общепринятой мерой беспорядка — энтропией.
Нам известно, что число реализаций выборки  а все реализации равновероятны. Энтропия в этом случае
а все реализации равновероятны. Энтропия в этом случае

Ранжированная выборка обладает энтропией, равной нулю. Уменьшение энтропии происходит, очевидно, в процессе упорядочения. Известно, что энтропия системы убывает в результате поступления информации, причем изменение энтропии равно количеству поступившей информации

Откуда берется эта информация, где ее источник? Вспомним, что процесс упорядочения базируется на элементарной операции — парном сравнении, в случае сортировки естественной выборки — на сравнении двух равновероятных объектов. Такое сравнение сопровождается порождением одной двоичной единицы информации.
Мы рассмотрели несколько ранжируклцих процедур и видели, что верхняя граница числа инверсий равна  что и определяет то количество информации, которое (в принципе) может быть «закачано» в выборку в процессе упорядочения.
что и определяет то количество информации, которое (в принципе) может быть «закачано» в выборку в процессе упорядочения.
Весьма существенным в дальнейшем окажется то, что процедура упорядочения эквивалентна сложным нелинейным операциям над выборочными значениями. Покажем это для простейшей операции — выбора медианного значения [4]. Воспользуемся единичной ступенчатой функцией от разности выборочных значений  Пусть функция
Пусть функция  может принимать три значения в зависимости от соотношения
может принимать три значения в зависимости от соотношения  при
при  при
при  при
при  Тогда процедура выбора медианного значения в выборке из трех элементов может быть выражена в виде нелинейной функции от выборочных значений
Тогда процедура выбора медианного значения в выборке из трех элементов может быть выражена в виде нелинейной функции от выборочных значений

Итак, номер места, которое в результате ранжирования займет выборочное значение, может быть определен путем нелинейного преобразования над выборкой. Возможно, следует подчеркнуть, что упорядочение объектов может совершаться человеком неосознанно, на основе «скрытого знания». Эту операцию способны выполнять и животные, причем нам неизвестно, по каким алгоритмам действует их мозг. Описанные выше формальные процедуры также достаточно эффективны, если сопоставлять, например, необходимое число парных сравнений с числом выборок, которое пришлось бы на одну «естественно» ранжированную.
Мы познакомились, таким образом, с процедурами формирования и упорядочения выборок, выяснили, что стоит за беглой фразой «образуем и упорядочим выборку», и готовы воспользоваться, наконец, этой выборкой для того, чтобы судить по ней о свойствах того множества, которое она представляет.
Но мы уже так основательно потрудились над естественной выборкой, искусственно придали ей столько новых черт, что возникает мысль, а осталось ли в ней что-нибудь естественное, несет ли она еще черты генеральной совокупности породившего ее объекта, можно ли по ней делать адекватные этому объекту выводы?
Подобные сомнения обычны в науке. Известно, например, что на них базировались возражения против применения оптических средств в астрономии. Как можно верить в то, что линзы дают объективную картину небесных явлений, говорили скептики, если каждому известно, что они неспособны даже просто показать объект в его естественном положении, а переворачивают его вверх ногами! Одной из заслуг Галилея как раз и является то, что он развеял эти сомнения относительно телескопа.
Действительно, «естественная» выборка в результате всех происшедших с нею трансформаций не могла, став ранжированной, не приобрести новых свойств. Она подвергнута нелинейным преобразованиям, она «накачана» информацией, она очень интересный объект. Исследуем его.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
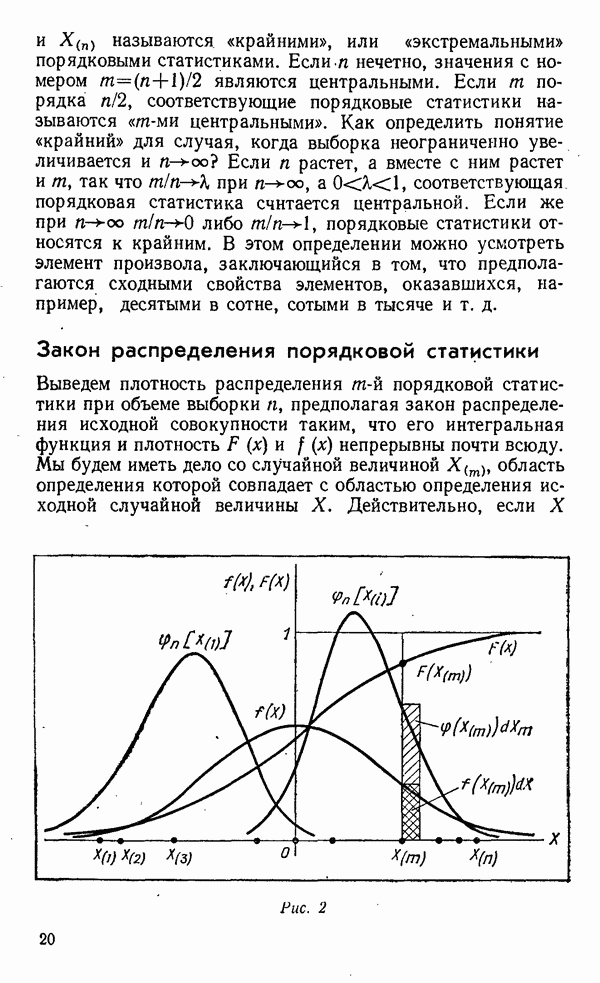
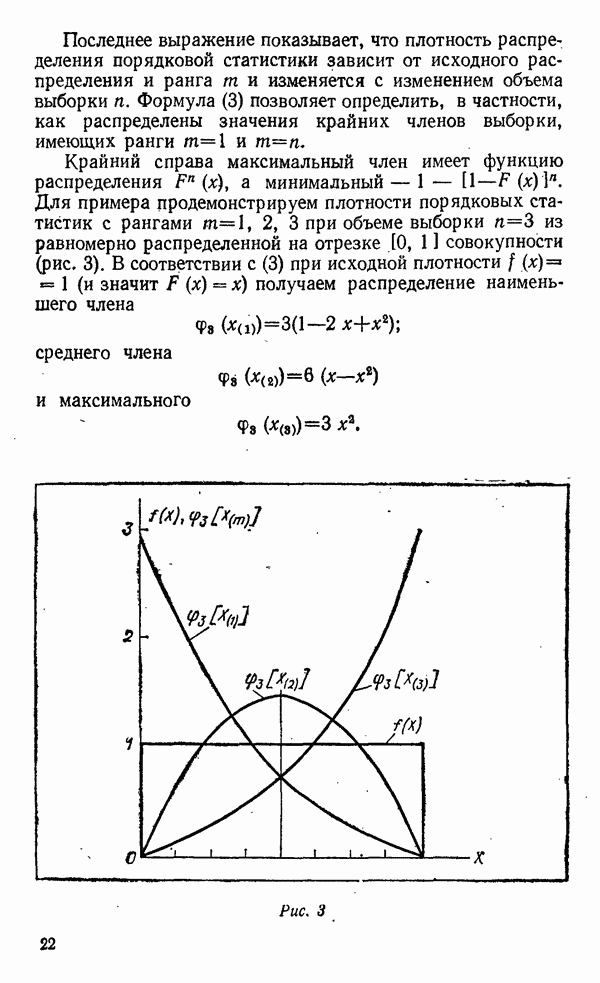
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
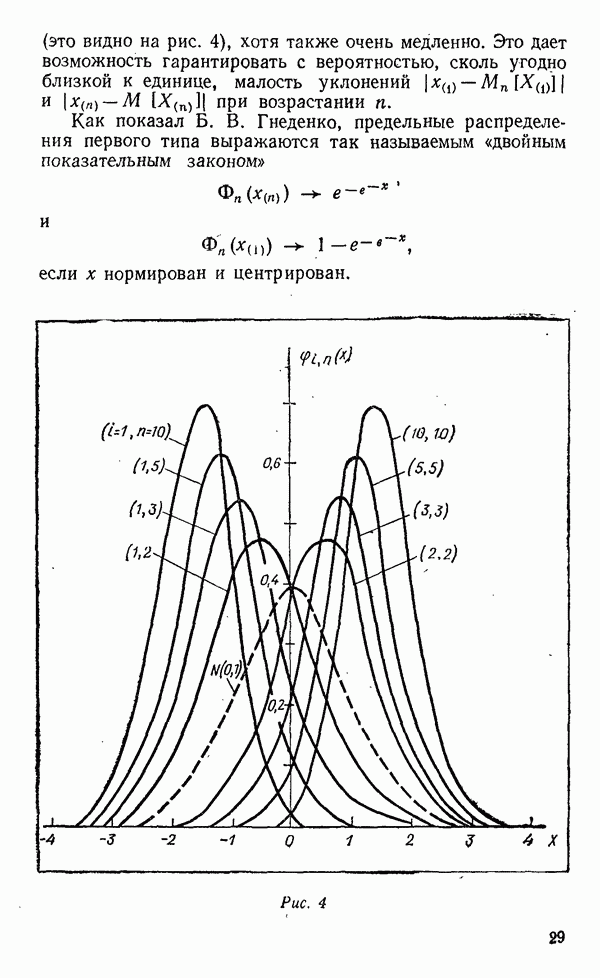
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
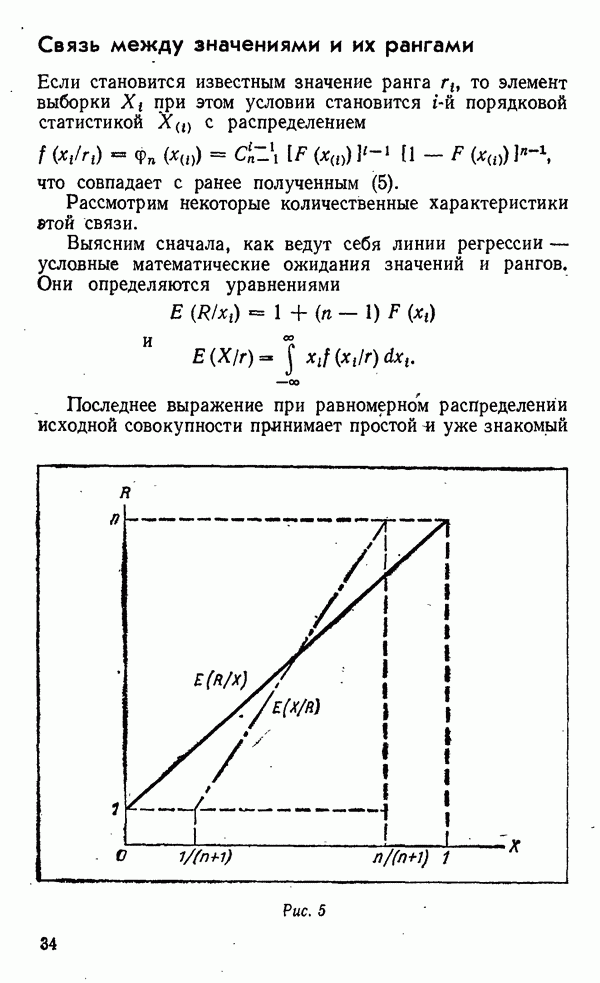
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
- Идентификация объекта с ненаблюдаемым входом
- Безэталонная классификация
- ЛИТЕРАТУРА