| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
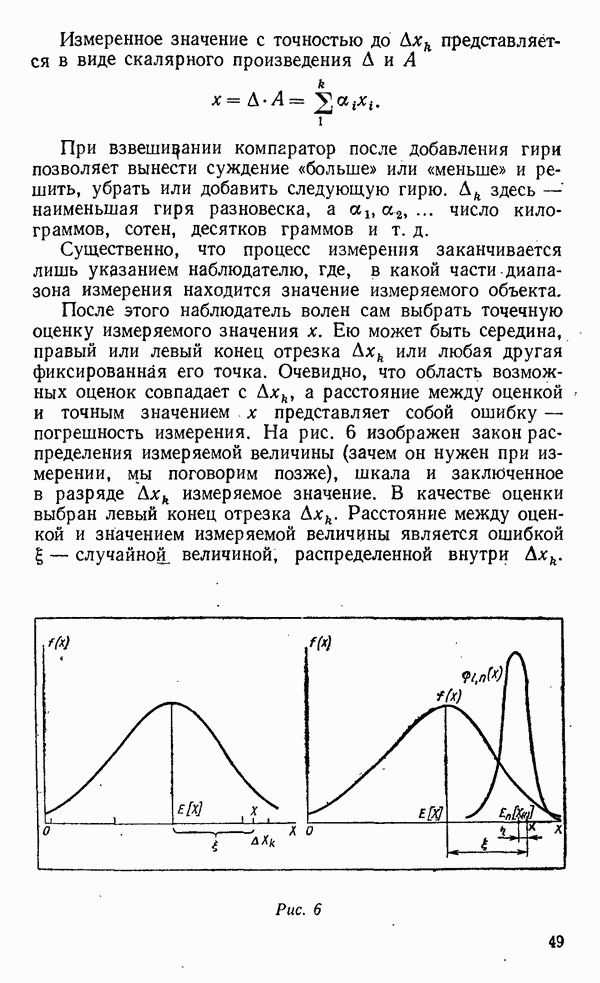
Закон распределения порядковой статистики
Выведем плотность распределения  порядковой статистики при объеме выборки
порядковой статистики при объеме выборки  предполагая закон распределения исходной совокупности таким, что его интегральная функция и плотность
предполагая закон распределения исходной совокупности таким, что его интегральная функция и плотность  и
и  непрерывны почти всюду. Мы будем иметь дело со случайной величиной
непрерывны почти всюду. Мы будем иметь дело со случайной величиной  область определения которой совпадает с областью определения исходной случайной величины
область определения которой совпадает с областью определения исходной случайной величины  Действительно, если X
Действительно, если X

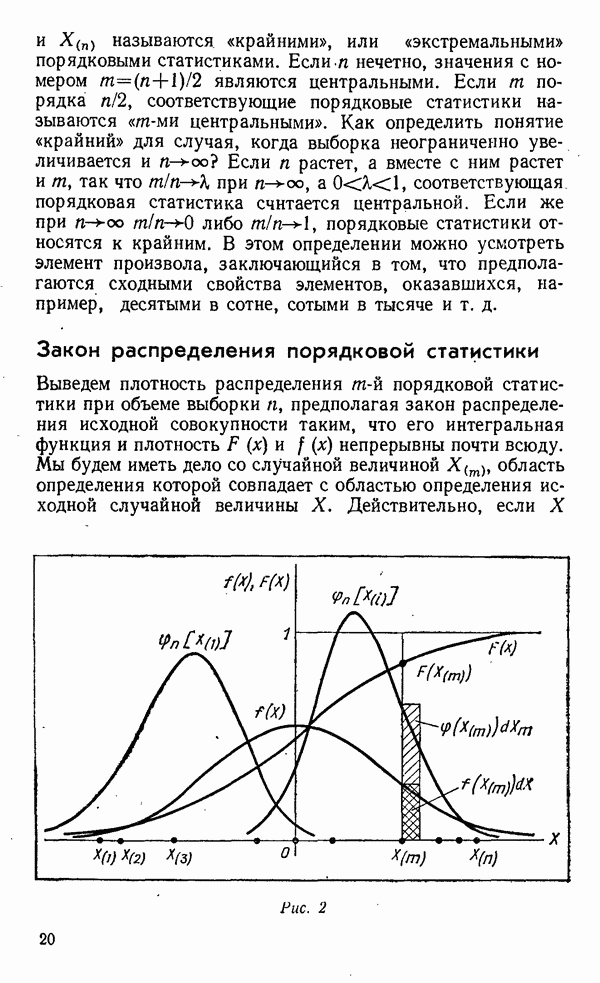
Рис. 2
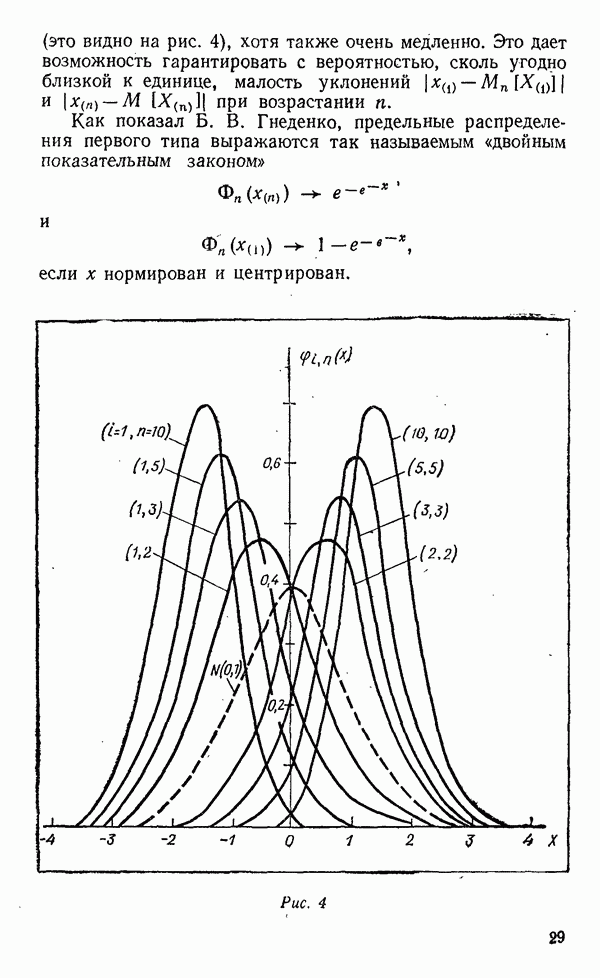
ограничена, то не могут появиться значения  (принадлежащие выборкам из X), выходящие за ее границы, и, наоборот, если X не ограничена, ничто не удержит
(принадлежащие выборкам из X), выходящие за ее границы, и, наоборот, если X не ограничена, ничто не удержит  каких-либо точных пределах.
каких-либо точных пределах.
Обратимся к рис. 2, на котором изображены функции  и искомая плотность распределения порядковой статистики
и искомая плотность распределения порядковой статистики  Индекс
Индекс  указывает объем выборки. На ось х нанесены значения
указывает объем выборки. На ось х нанесены значения  принадлежащие некоторой конкретной выборке. Запишем элемент вероятности
принадлежащие некоторой конкретной выборке. Запишем элемент вероятности  равный вероятности для порядковой статистики
равный вероятности для порядковой статистики  оказаться вблизи точки
оказаться вблизи точки 

Выразим эту же вероятность через исходный закон распределения, связав таким образом  Будем считать, что процесс образования выборки
Будем считать, что процесс образования выборки  процесс независимых испытаний, в которых «успехом» считается появление значения
процесс независимых испытаний, в которых «успехом» считается появление значения  а «неуспехом»
а «неуспехом»  Очевидно, что вероятность успеха
Очевидно, что вероятность успеха  а неуспеха
а неуспеха  (рис. 2). Количество «успехов» равно
(рис. 2). Количество «успехов» равно  «неуспехов»
«неуспехов»  поскольку
поскольку  значение
значение  в выборке объема
в выборке объема  таково, что
таково, что  значений меньше и
значений меньше и  значений больше его.
значений больше его.
Нетрудно видеть, что речь идет о процедуре подсчета вероятностей, сходной с той, которая приводит к биномиальному закону распределения.
Вероятность для исходной случайной величины принять значение, близкое к  есть элемент вероятности
есть элемент вероятности 
Вероятность расположения выборки вокруг значения  так, что
так, что  элементов ее окажутся слева,
элементов ее окажутся слева,  справа, а сама случайная величина X вблизи него и будет равной
справа, а сама случайная величина X вблизи него и будет равной

Но именно эта вероятность и определяется выражением  Поэтому, приравняв (1) и (2), получим
Поэтому, приравняв (1) и (2), получим

Если при переходе от плотности  сохранить масштаб по оси х, то
сохранить масштаб по оси х, то

Последнее выражение показывает, что плотность распределения порядковой статистики зависит от исходного распределения и ранга  и изменяется с изменением объема выборки
и изменяется с изменением объема выборки  Формула (3) позволяет определить, в частности, как распределены значения крайних членов выборки, имеющих ранги
Формула (3) позволяет определить, в частности, как распределены значения крайних членов выборки, имеющих ранги 
Крайний справа максимальный член имеет функцию распределения  а минимальный
а минимальный  Для примера продемонстрируем плотности порядковых статистик с рангами
Для примера продемонстрируем плотности порядковых статистик с рангами  при объеме выборки
при объеме выборки  из равномерно распределенной на отрезке [0, 11 совокупности (рис. 3). В соответствии с (3) при исходной плотности
из равномерно распределенной на отрезке [0, 11 совокупности (рис. 3). В соответствии с (3) при исходной плотности  (и значит
(и значит  получаем распределение наименьшего члена
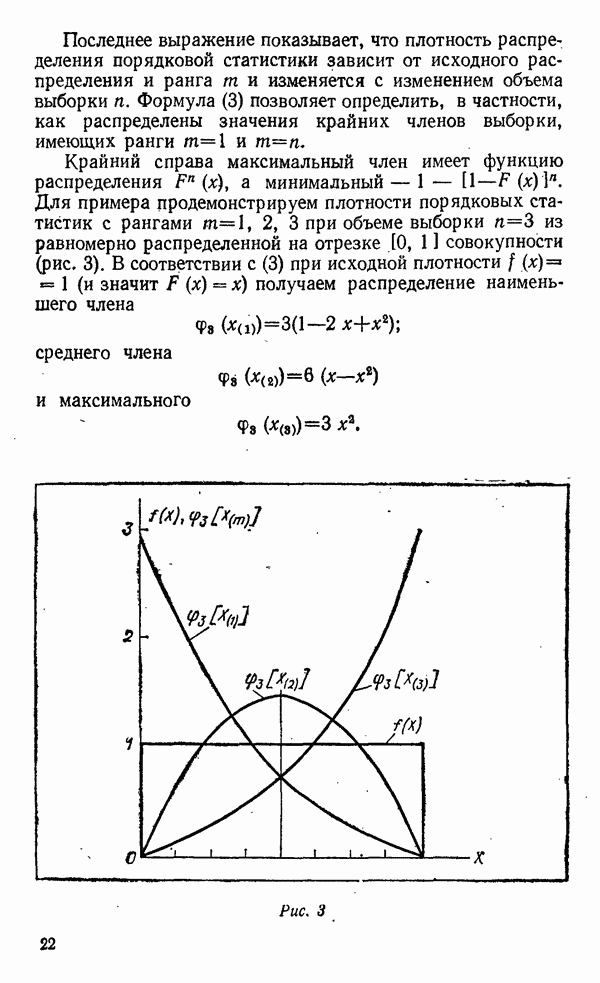
получаем распределение наименьшего члена

среднего члена

и максимального


Рис. 3
Эти плотности изображены на рис. 3. В полном согласии с интуитивными представлениями плотность центрального члена выборки симметрична относительно медианы исходного распределения, а плотности крайних ограничены тем же интервалом, что и  и возрастают к соответствующей границе.
и возрастают к соответствующей границе.
Продемонстрируем на этом же примере еще одно любопытное свойство распределений порядковых статистик. Сложим плотности  и разделим результат на их число:
и разделим результат на их число:

на отрезке [0, 1].
Сумма (нормированная) плотностей порядковых статистик оказалась равной исходной плотности  Это значит, что генеральная совокупность X является смесью порядковых статистик
Это значит, что генеральная совокупность X является смесью порядковых статистик  Этого результата следовало ожидать. Выше мы уже упоминали, что, рассортировав исходную совокупность по рангам, мы могли бы, вновь смешав объекты с различными рангами, восстановить ее. Теперь мы убедились в этом на примере, но можно было бы привести и строгое доказательство этого свойства.
Этого результата следовало ожидать. Выше мы уже упоминали, что, рассортировав исходную совокупность по рангам, мы могли бы, вновь смешав объекты с различными рангами, восстановить ее. Теперь мы убедились в этом на примере, но можно было бы привести и строгое доказательство этого свойства.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
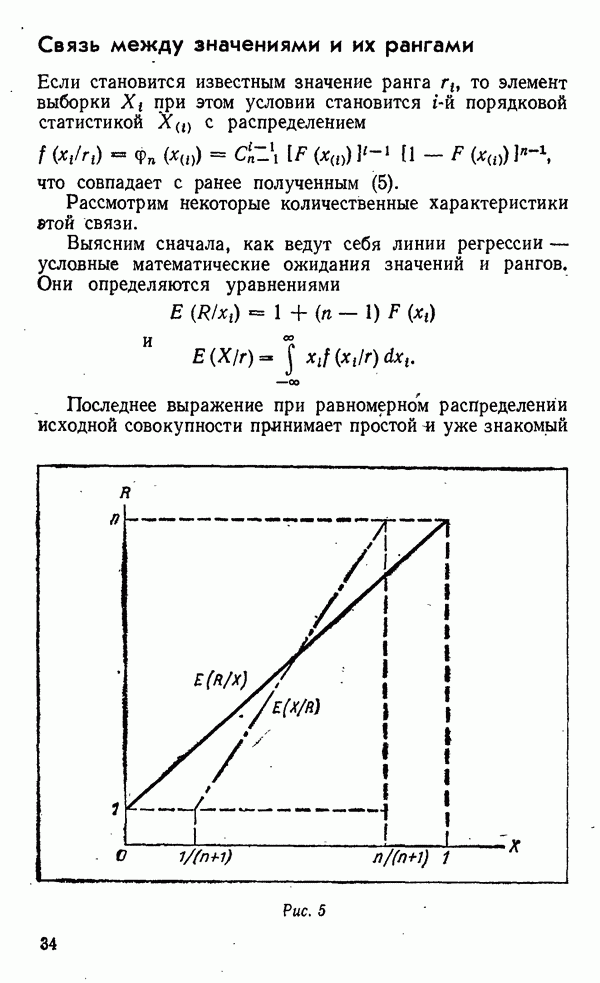
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
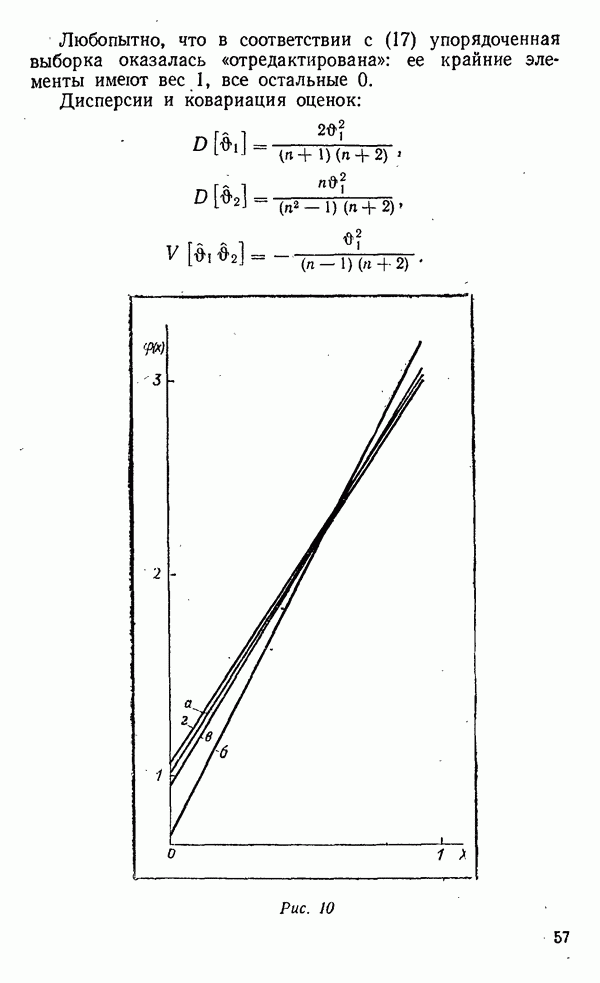
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
- Идентификация объекта с ненаблюдаемым входом
- Безэталонная классификация
- ЛИТЕРАТУРА