| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
Оперировать выборкой вместо совокупности — обычный исследовательский прием. Прибегают к нему по нескольким причинам. Во-первых, зачастую оказывается физически невозможным подвергнуть контролю всю генеральную совокупность. Кроме того, нередки случаи, когда испытание образца — элемента совокупности связано с его порчей или утратой. Наконец, «выборочный метод» [1], если он правильно применен, может дать вполне приемлемую точность.
Поскольку нашей темой являются свойства упорядоченной выборки, начнем с того, как получить и упорядочить выборку.
«Будем оценивать свойства закона распределения генеральной совокупности X по выборке из  независимых значений
независимых значений 
«Образовав выборку, ранжируем ее значения»...
Для тех, кто часто общается с литературой по теории вероятностей и математической статистике, приведенные формулировки настолько привычны, что не задерживаются в сознании, а для тех, кто встречается с ними нечасто, они представляют определенную опасность, поскольку могут создать иллюзию, будто образовать выборку для последующих (законных!) выводов по ней легко и просто.
Рассмотрим повнимательнее понятия «образование выборки» и «ранжирование выборки».
Образование выборки
Вам укололи палец, выдавили из него капельку крови и через некоторое время объявили, что содержание гемоглобина в норме. Где же «все в порядке» с гемоглобином — в пальце,
откуда бралась проба крови? Да нет, результат анализа мы смело переносим на весь объем крови в организме. Эта уверенность базируется, во-первых, на допущении, что в процессе кровообращения кровь перемешивается достаточно хорошо, а во-вторых, на том, что предыдущее предположение не противоречит практике.
Таким образом, перед нами пример того, как малая проба хорошо отражает свойства некоторого объекта в целом. К сожалению, так бывает далеко не всегда. Когда, например, на элеватор приходит машина с хлебом и требуется определить его влажность, пробы, взятые из разных точек объема зерна, могут дать существенно различные результаты хотя бы в силу того, что верхний слой мог просохнуть в пути либо, напротив, намокнуть.
Если поручить неподготовленному человеку набрать пробу кускового материала — щебня, угля, руды и т. д. — для определения состава по крупности, можно наблюдать интересную картину того, как образны, заполнившие контейнер, будут бессознательно подобраны им «по руке» — ни мелочь, ни крупные глыбы не войдут в пробу.
Таким образом, для организации «репрезентативной» (представительной) выборки, выборки, хорошо отражающей свойства всей «генеральной совокупности», необходимо затратить специальные усилия. Существуют инструкции по отбору проб воздуха, воды, сыпучих веществ и т. д., обеспечивающие представительность выборок.
Кроме представительности, «хорошая» выборка должна состоять из независимых элементов. Это свойство также нелегко обеспечить в целом ряде испытаний. При отборе пробы кускового материала человек, положив в контейнер несколько крупных камней, как правило, «компенсирует» их целой пригоршней мелочи, причем делает это бессознательно.
В книге У. Кокрена [1] приводится несколько распространенных способов отбора, различающихся принципом, на котором построена процедура.
1. Отбор, ограничивающийся легко доступной частью совокупности. Например, выборка угля из открытого вагона берется с небольшой глубины.
2. Отбор производится беспорядочно. Исследователь, выбирая десять кроликов из большой клеткив лаборатории, может делать это без продуманного плана.
3. Имеется небольшая, но неоднородная совокупность. Исследователь просматривает всю совокупность и
отбирает небольшое число «типичных» единиц, т. е. единиц, огвечающих его представлению о среднем для совокупности. Такой метод называют иногда предвзятым или направленным отбором.
4. Выборка состоит преимущественно из добровольцев в исследованиях, где процесс измерения опасен или неприятен для обследуемого.
Очевидно, наилучшие результаты давала бы процедура отбора, исключающая участие человека в процессе принятия решения — включать или не включать данный образец в выборку. Существуют устройства вроде тех, что выбрасывают шары с номерами «Спортлото», либо программы, генерирующие случайные последовательности чисел, все они призваны выдавать статистически независимые и представительные выборки. В нашем примере с отбором пробы кускового материала следовало бы поступить следующим образом. Во-первых, все объекты исходной совокупности, куски, пронумеровать. Далее, обратиться к генератору случайных чисел и извлекать из кучи щебня те камни, чьи. номера названы генератором. Эта процедура должна повторяться до тех пор, пока не будет сформирована выборка нужного объема.
Понятно, что описанный эксперимент нереален и может рассматриваться как некоторая «идеальная» процедура, к которой мы, впрочем, будем обращаться в дальнейшем.
Вот как образуют случайную выборку на практике при переписи населения [1], когда нужно задать дополнительные вопросы небольшой группе граждан: «В США 5 %-ная выборка была впервые применена в переписи 1940 г., когда дополнительные вопросы о роде занятий, происхождении, числе детей и т. д. задавали лицам, чьи фамилии падали на две из каждых 40 строк на лицевой и оборотной сторонах переписного листа. При переписи 1950 г. по 20 %-ной выборке (каждая пятая строка переписного листа) были получены сведения по таким данным, как доход, число лет обучения, миграции, служба в вооруженных силах. Путем отбора из этой 20 %-ной выборки каждого шестого человека дополнительно была получена выборка, дающая сведения о браках и числе рожденных детей. Кроме того, группа вопросов, касающихся сроков службы и состояния жилйца, была разбита на пять подгрупп и ответы на вопросы были получены в каждом пятом доме».
Обратим внимание на то, что, генерируя выборку при помощи того или иного источника случайных чисел, мы
получаем набор значений  из некоторой генеральной совокупности значений х, а извлекая камешки из кучи щебня (множества К), мы образуем набор объектов
из некоторой генеральной совокупности значений х, а извлекая камешки из кучи щебня (множества К), мы образуем набор объектов 
Измеряя, взвешивая, сжргая затем объекты  мы получаем соответствующие им значения линейных размеров, масс, количества выделяющегося тепла — значения случайных параметров, описывающих множество К.
мы получаем соответствующие им значения линейных размеров, масс, количества выделяющегося тепла — значения случайных параметров, описывающих множество К.
В руководствах по выборочному методу, как, например, у. У. Кокрена, отмечается, что большое значение имеет и правильный выбор элементов я — единиц отбора: «Эти единицы должны вместе исчерпывать всю совокупность и не должны перекрывать одна другую, т. е. каждый элемент совокупности должен принадлежать одной и толькой одной единице. Иногда единицы выделяются очевидным образом, как, например, в совокупности электрических лампочек, где единицей отбора служит отдельная лампочка. Иногда приходится выбирать из нескольких возможных единиц отбора. Например, при обследовании людей в городе единицей отбора может быть отдельный человек, члены одной семьи или же все жители городского квартала. При выборочном изучении урожая сельскохозяйственных культур единицами отбора могут служить поля, фермы или же участки земли, форма и размеры которых заранее известны».
Здесь же существенно то, что, образовав выборку объектов  нам понадобится воспользоваться еще и измерительным прибором для того, чтобы образовать выборку
нам понадобится воспользоваться еще и измерительным прибором для того, чтобы образовать выборку  присущих этим объектам значений.
присущих этим объектам значений.
Кое-что о порядке
Прежде чем «наводить порядок» в выборке, вспомним кое-что о понятии «порядок», для чего будем рассматривать нашу выборку как некоторое множество, состоящее из  элементов.
элементов.
Между элементами всякого множества можно устанавливать некоторые отношения, задаваемые набором определенных свойств. Так, отношение между элементами множества именуется отношением эквивалентности, если оно обладает свойствами рефлексивности, симметричности и транзитивности. Например, обычное равенство на множестве чисел есть отношение эквивалентности. Мы будем говорить в дальнейшем об отношениях порядка.
Отношений порядка между элементами множества
можно установить несколько, в зависимости от требований к Характеру упорядоченности [21.
Говорят о порядках строгих и нестрогих, совершенных в несовершенных, линейных и древовидных [31.
Разный смысл можно вложить и в само слово «порядок». Расположение вещественных чисел по возрастанию есть порядок по отношению «больше».
Пусть М — некоторое множество, а  множество его подмножеств. Включение
множество его подмножеств. Включение  является отношением, устанавливающим порядок на
является отношением, устанавливающим порядок на  Это — порядок по отношению «быть подмножеством».
Это — порядок по отношению «быть подмножеством».
Тип упорядочения, очевидно, будет зависеть от того, считаем ли мы возможным, чтобы каждый объект мог быть подчинен самому себе (как в случае нестрогого неравенства ( или нестрогого включения С), или, наоборот, считаем, что объект не может быть старше самого себя (строгие неравенство С и включение С).
или нестрогого включения С), или, наоборот, считаем, что объект не может быть старше самого себя (строгие неравенство С и включение С).
В зависимости от этих предпосылок упорядоченность может быть «частичной» и «строгой».
Отношение на множестве называется частичным порядком, если оно рефлексивно, транзитивно и антисимметрично.
Отношения  и
и  являются отношениями частичного порядка.
являются отношениями частичного порядка.
Определим отношение  множестве
множестве  для
для  отношение
отношение  имеет место тогда и только тогда, когда
имеет место тогда и только тогда, когда  Если
Если  мы говорим, что а предшествует
мы говорим, что а предшествует  (меньше
(меньше  или что
или что  следует за а (больше а).
следует за а (больше а).
Отношение «С задает на множестве М строгий порядок. Оно антирефлексивно, транзитивно и антисимметрично. Это означает:
ни для какого  не выполнимо
не выполнимо 
если  то выполнено
то выполнено 
если выполнено  то невозможно
то невозможно 
Первые два свойства образуют определение строгого порядка, а третье из них следует.
Дальнейшее развитие понятия «порядок» связано с вопросом, все ли элементы множества попарно сравнимы между собой. Рассмотрим его на примере упорядочивания по включению [2].
Пусть М — множество русских слов. Слово х «старше» слова у, если у можно получить из х вычеркиванием нескольких букв слева и (или) справа. Это отношение (обозначим его  задает на множестве русских слов
задает на множестве русских слов
некоторую упорядоченность. Например, «стол» < «столовая», «беда» < «победа». Но слова «облако» и «облатка» несравнимы. На рис. 1 показан фрагмент графа, изображающего старшинство (в указанном смысле) слов. Мы видим, что все слова, входящие в граф, младше слова «коловорот», но не все сравнимы между собой. Отношение старшинства не может быть установлено для слов «кол», «олово», «ворота ит.д.
Существуют множества (например, множество вещественных чисел), для которых отношение порядка (строгого или нестрогого) может быть установлено между любыми элементами.
В зависимости от этого порядок подразделяют на «совершенный» и «несовершенный».
Отношение частичного (строгого) порядка  называется совершенным (иначе — линейным) порядком тогда и только тогда, когда
называется совершенным (иначе — линейным) порядком тогда и только тогда, когда  или а
или а  для всех
для всех  Если
Если  совершенный порядок в М, упорядоченная пара
совершенный порядок в М, упорядоченная пара  называется линейно упорядоченным множеством или цепью.
называется линейно упорядоченным множеством или цепью.
В соответствии с этим определением частичный порядок на множестве натуральных чисел — совершенный, а строгий порядок на рис. 1 не является совершенным,

Рис. I
Наличие несравнимых элементов заставляет определить и понятия непосредственного следования элементов друг за другом, а также понятия минимальный (максимальный) и наименьший (наибольший) элементы.
Если  частичный (строгий) порядок на множестве М, элемент
частичный (строгий) порядок на множестве М, элемент  называют непосредственно следующим за элементом
называют непосредственно следующим за элементом  тогда и только тогда, когда
тогда и только тогда, когда  и не существует такого
и не существует такого  что
что  Элемент а называют непосредственно предшествующим
Элемент а называют непосредственно предшествующим 
Пусть множество  частично упорядочено по С. Здесь (1, 2, 3) непосредственно следует за
частично упорядочено по С. Здесь (1, 2, 3) непосредственно следует за  непосредственно следует как за (1), так и за (2). Но (1, 2, 3) не следует непосредственно ни за (1) ни за (2), поскольку
непосредственно следует как за (1), так и за (2). Но (1, 2, 3) не следует непосредственно ни за (1) ни за (2), поскольку  . Подмножества же (1) и (2) несравнимы и ни одно из них не может непосредственно следовать за другим.
. Подмножества же (1) и (2) несравнимы и ни одно из них не может непосредственно следовать за другим.
Очевидно, лишь при строгом совершенном порядке все элементы упорядоченного множества являются непосредственно следующим (либо предшествующими).
Далее, на множестве с заданным отношением порядка элемент  называют минимальным, если не существует другого элемента а
называют минимальным, если не существует другого элемента а  такого, что
такого, что 
Ясно, что для цепей понятие минимального элемента совпадает с понятием наименьшего элемента. В противном случае может оказаться, что элемент минимален, но не находится в соотношении  с какими-либо иными элементами. Так, на рис. 1 слова
с какими-либо иными элементами. Так, на рис. 1 слова  и «от» — минимальные элементы, но не находятся друг с другом в отношении порядка (несравнимы). Слово же «коловорот» является одновременно и максимальным, и наибольшим элементом.
и «от» — минимальные элементы, но не находятся друг с другом в отношении порядка (несравнимы). Слово же «коловорот» является одновременно и максимальным, и наибольшим элементом.
Если на множестве М задан совершенный строгий порядок и множество М конечно, то существует единственный максимальный (минимальный) элемент.
Пусть на множестве М определена функция  принимающая вещественные числовые значения.
принимающая вещественные числовые значения.
Функция называется сохраняющей порядок относительно порядка на М и порядка <на  том случае, если
том случае, если  в М влечет за собой
в М влечет за собой 
Наконец, приведем одну важную теорему, позволяющую связать значение элемента выборки с его местом в упорядоченном ряду.
Пусть, на конечном множестве М существует отношение совершенного строгого порядка. Тогда для подмножества  можно выбрать такую нумерацию элементов
можно выбрать такую нумерацию элементов
 что соотношение
что соотношение  будет выполняться в том и только в том случае, если
будет выполняться в том и только в том случае, если 
Эта теорема утверждает, что любой совершенный строгий порядок на конечном множестве равносилен обычному порядку на некотором отрезке натурального ряда. Если же порядок на М не является совершенным, то, очевидно, элементы этого множества нельзя перенумеровать так, чтобы большим номерам соответствовали старшие элементы.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
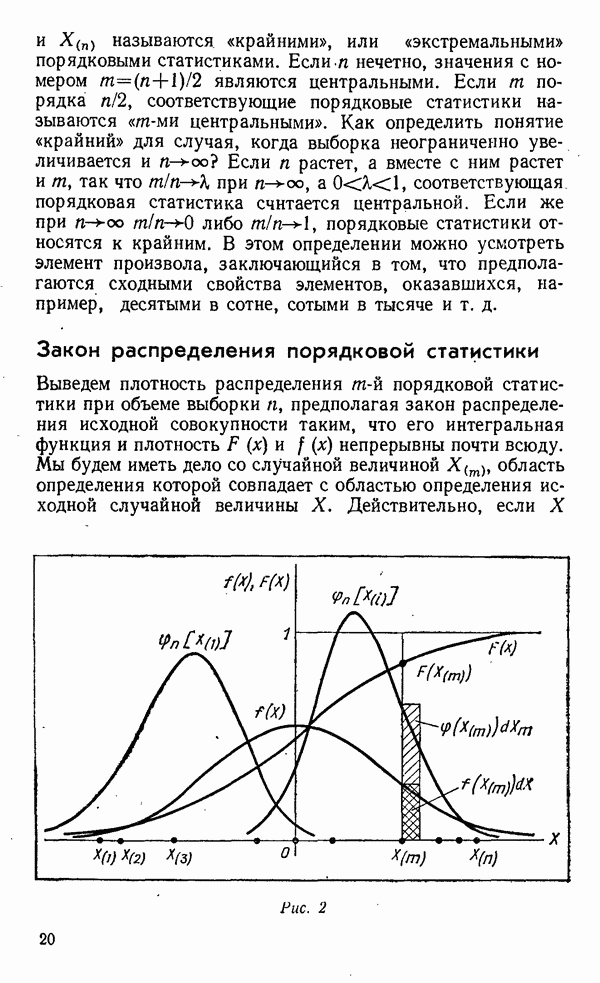
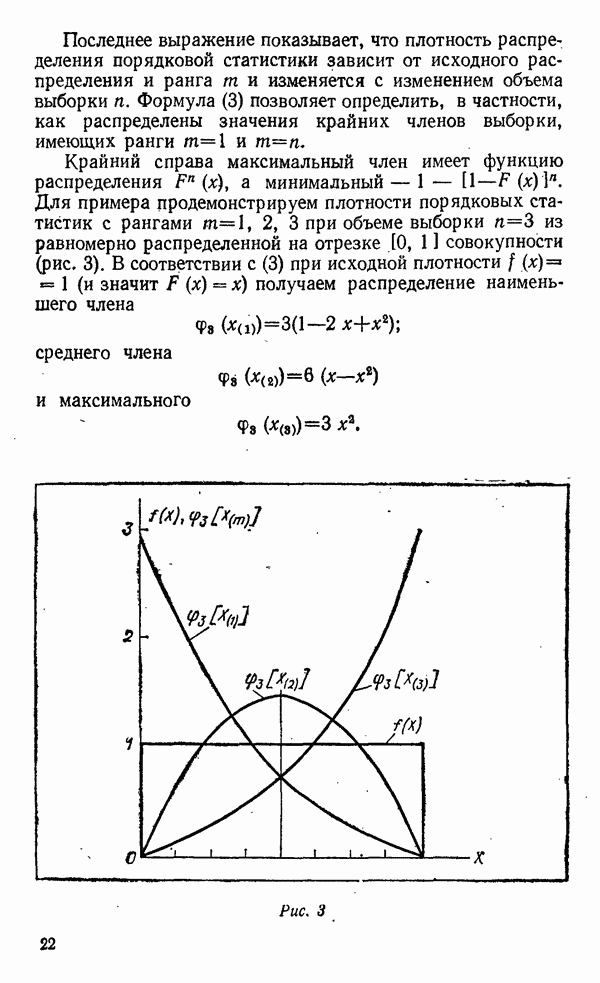
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
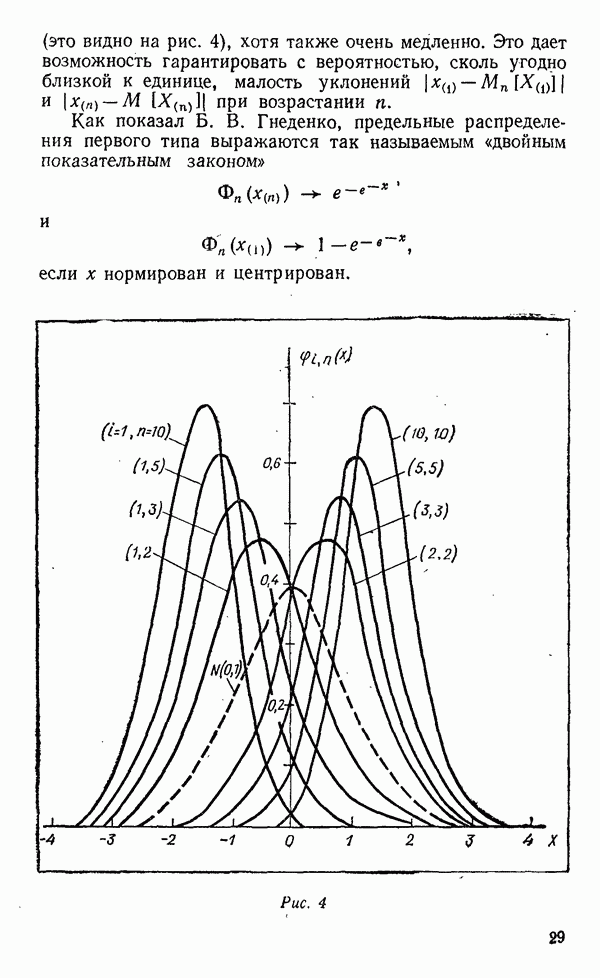
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
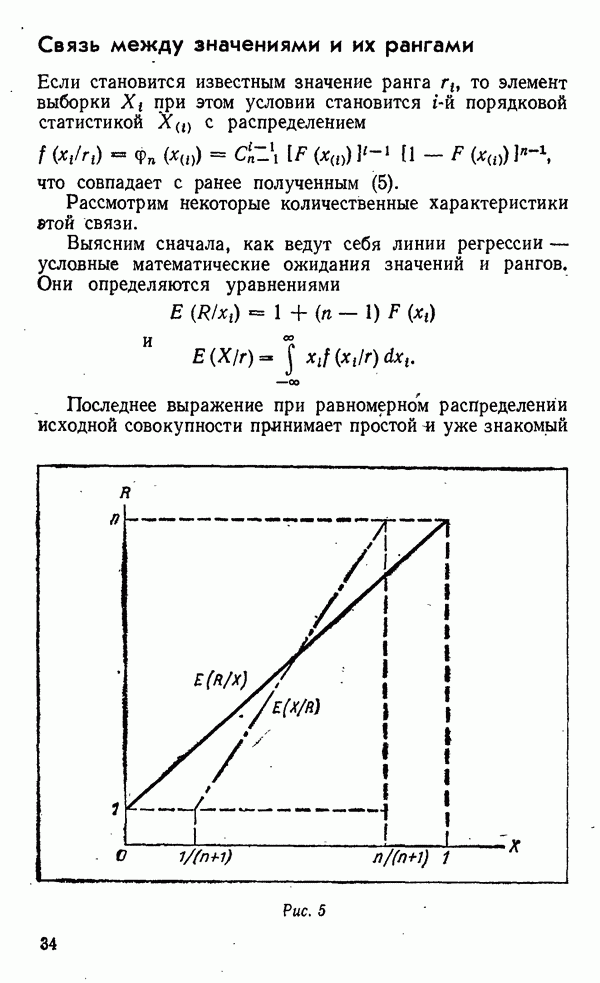
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
- Идентификация объекта с ненаблюдаемым входом
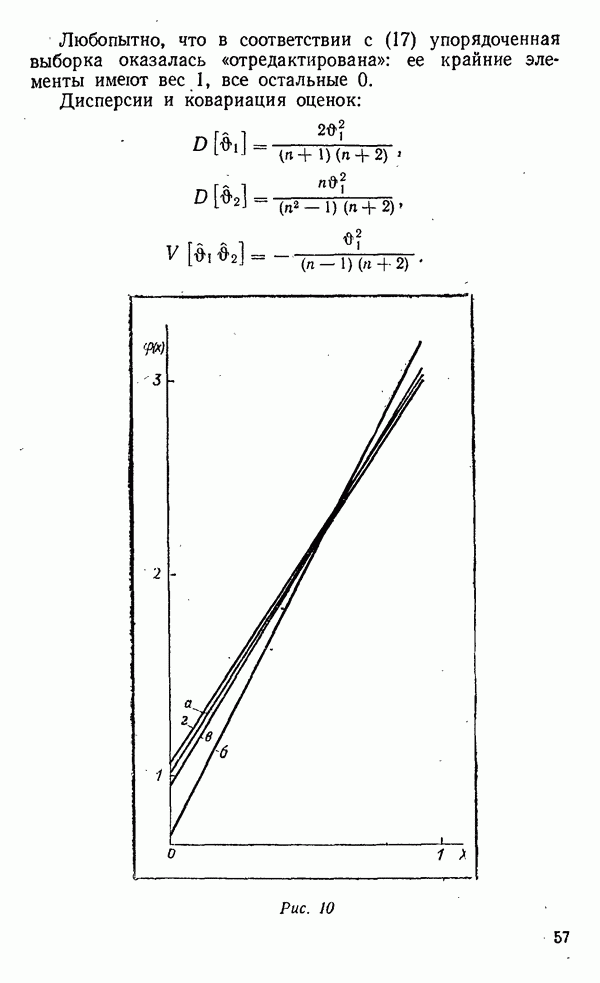
- Безэталонная классификация
- ЛИТЕРАТУРА