| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Ранговая корреляция
Наберем камешков из кучи щебня (камешки, как мы помним, пронумерованы), взвесим их, получив выборку значений  и измерим наибольший линейный размер каждого, образовав выборку значений
и измерим наибольший линейный размер каждого, образовав выборку значений  другой случайной величины
другой случайной величины  максимального линейного размера. По физической сущности объекта ясно, что
максимального линейного размера. По физической сущности объекта ясно, что  статистически связаны — более тяжелый образец в среднем и больший. Мерой связи выступает коэффициент корреляции
статистически связаны — более тяжелый образец в среднем и больший. Мерой связи выступает коэффициент корреляции

оценка которого может быть определена по выборкам 
Мы выяснили, однако, что, упорядочив выборки  и оперируя их рангами
и оперируя их рангами  мы можем в принципе располагать той же информацией, что содержалась и в исходных выборках. Значит ли это,
мы можем в принципе располагать той же информацией, что содержалась и в исходных выборках. Значит ли это,  коэффициент корреляции между случайными величинами
коэффициент корреляции между случайными величинами  отразит степень зависимости
отразит степень зависимости 
Да, дело обстоит именно так. Выясним только, что значит «упорядочим выборки  Ранжировав
Ранжировав  и записав последовательность
и записав последовательность  мы получим случайную перестановку значений вектора К. Попытавшись проделать эту процедуру с конца, мы придем к тому же: ранжированной станет выборка
мы получим случайную перестановку значений вектора К. Попытавшись проделать эту процедуру с конца, мы придем к тому же: ранжированной станет выборка  а последовательность значений
а последовательность значений  превратится в случайную перестановку.
превратится в случайную перестановку.
Поступим следующим образом. Поставим в обеих выборках на места  соответствующие ранги
соответствующие ранги  получим две случайные перестановки
получим две случайные перестановки  и
и  и вычислим коэффициент корреляции йежду ними — ранговый коэффициент корреляции Спирмена.
и вычислим коэффициент корреляции йежду ними — ранговый коэффициент корреляции Спирмена.

Коэффициент этот «устроен» обычно, сравним его с (9). Здесь  выборочные значения случайных величин,
выборочные значения случайных величин,  среднее арифметическое рангов (первых
среднее арифметическое рангов (первых  чисел натурального ряда)
чисел натурального ряда)

 их дисперсия.
их дисперсия.
Есть смысл переписать (10) более компактно

Коэффициент  носит имя психолога Спирмена, который ввел его для обнаружения связи между признаками, не имеющими количественного выражения. Если упорядочения по этим признакам - статистически связаны, коэффициент
носит имя психолога Спирмена, который ввел его для обнаружения связи между признаками, не имеющими количественного выражения. Если упорядочения по этим признакам - статистически связаны, коэффициент  принимает положительные значения, когда большая выраженность одного признака соответствует
принимает положительные значения, когда большая выраженность одного признака соответствует
большему проявлению другого. В противном случае  отрицателен. Так [9], если речь идет об успехах детей в учебе и спорте, можно составить два списка учащихся класса, в которых фамилии пойдут в порядке возрастания успеваемости в учебе и успехов в спорте. Возьмем за основу нумерацию, Данную первым списком. Номера во втором списке окажутся при этом рангами, которые ученики получают при упорядочении по второму признаку. Если между двумя признаками нет никакой зависимости, не будет никакой связи и между номерами в двух списках — в качестве второй нумерации
отрицателен. Так [9], если речь идет об успехах детей в учебе и спорте, можно составить два списка учащихся класса, в которых фамилии пойдут в порядке возрастания успеваемости в учебе и успехов в спорте. Возьмем за основу нумерацию, Данную первым списком. Номера во втором списке окажутся при этом рангами, которые ученики получают при упорядочении по второму признаку. Если между двумя признаками нет никакой зависимости, не будет никакой связи и между номерами в двух списках — в качестве второй нумерации  равными шансами могла бы появиться любая.
равными шансами могла бы появиться любая.
Коэффициент Спирмена наиболее употребителен среди возможных ранговых мер статистической связи вследствие своей простоты, но он далеко не единственный. Применяются еще и «коэффициенты беспорядка» [5]. Пусть значения, рангов  располагаются в натуральном порядке
располагаются в натуральном порядке  а соответствующие ранги К, образующие перестановку
а соответствующие ранги К, образующие перестановку  равны
равны  Естественный метод измерения беспорядка
Естественный метод измерения беспорядка  -рангов, т. е. отклонения
-рангов, т. е. отклонения  от порядка
от порядка  состоит в подсчете числа инверсий между ними. Например, при
состоит в подсчете числа инверсий между ними. Например, при  в
в  -ранжировке 3214 имеются три инверсии, а именно
-ранжировке 3214 имеются три инверсии, а именно  Число таких инверсий, обозначаемое
Число таких инверсий, обозначаемое  может изменяться от О до
может изменяться от О до  Коэффициент беспорядка
Коэффициент беспорядка

заключен в пределах 
Коэффициент  можно «улучшить», если придавать инверсиям различный вес, например в ранжировке 24351 чувствуется, что инверсия 5—1 должна иметь больший вес, чем инверсия 4—3, поскольку она представляет собой более серьезное отклонение от натурального порядка
можно «улучшить», если придавать инверсиям различный вес, например в ранжировке 24351 чувствуется, что инверсия 5—1 должна иметь больший вес, чем инверсия 4—3, поскольку она представляет собой более серьезное отклонение от натурального порядка  Наиболее простой способ взвешивания — «измерение» расстояния между рангами, образующими инверсию; в приведенном только что примере это дало бы соответственна веса 4 и 1 двум инверсиям. Однако использование весов
Наиболее простой способ взвешивания — «измерение» расстояния между рангами, образующими инверсию; в приведенном только что примере это дало бы соответственна веса 4 и 1 двум инверсиям. Однако использование весов  возвращает нас к коэффициенту Спирмена, основанному, как мы видим, на сумме квадратов этих весов.
возвращает нас к коэффициенту Спирмена, основанному, как мы видим, на сумме квадратов этих весов.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
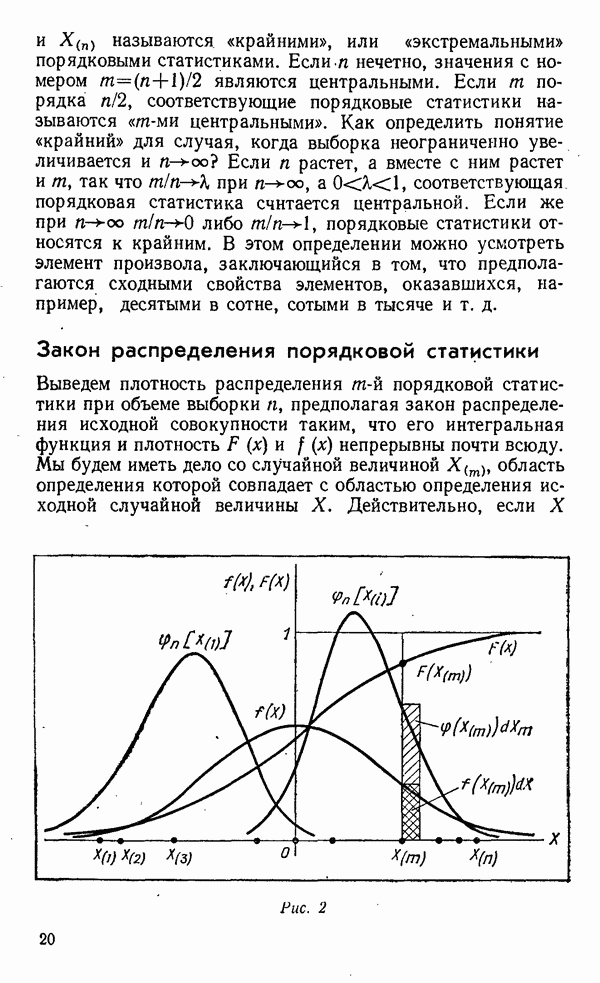
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
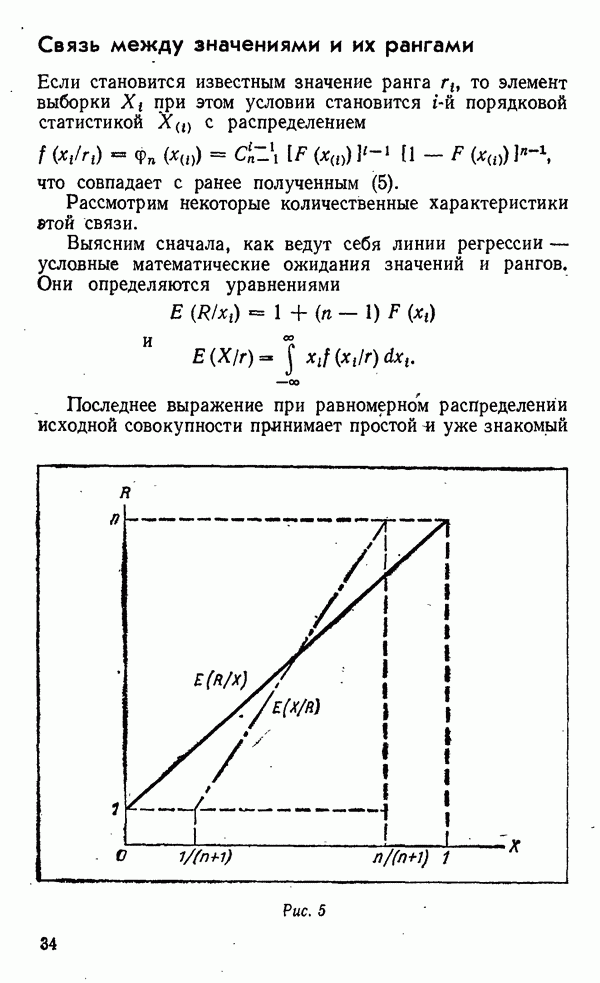
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
- Идентификация объекта с ненаблюдаемым входом
- Безэталонная классификация
- ЛИТЕРАТУРА