| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Цензурирование выборок — общая идея
Среднее арифметическое выборки  являясь оценкой среднего, имеет вид:
являясь оценкой среднего, имеет вид:

Понятно, что вычисление среднего арифметического ранжированной выборки  дает тот же результат
дает тот же результат

Отбрасывание крайних членов выборки (наименьших  и наибольших
и наибольших  выразится в том, что в (12) суммирование будет производиться в пределах
выразится в том, что в (12) суммирование будет производиться в пределах 

что естественно, отразится на свойствах  как оценки среднего.
как оценки среднего.
Выражение (13) можно трактовать, как суммирование порядковых статистик с весами. Наименьшие и наибольшие статистики получили веса, равные нулю, а все остальные — единице. К такому цензурированию приводило основанное на интуиции отбрасывание крайних членов. Гораздо более гибким оказалось взвешивание всех слагаемых (12), приводящее к линейной операции над порядковыми статистиками, когда вычисляется оценка

Наборы коэффициентов  характеризуют степень доверия к значениям
характеризуют степень доверия к значениям  но выбираются не произвольно, а в зависимости от критерия точности оценки, закона распределения совокупности X, объема выборки
но выбираются не произвольно, а в зависимости от критерия точности оценки, закона распределения совокупности X, объема выборки  Укажем следуя
Укажем следуя  некоторые свойства коэффициентов
некоторые свойства коэффициентов  в зависимости от типов оценок
в зависимости от типов оценок 
Во-впервых, часть коэффициентов принимает постоянные и равные значения, а остальные равны нулю. При этом часть порядковых статистик равномерно усредняется, а часть отбрасывается. Если отбрасываются крайние порядковые статистики, говорят что оценки получены по усеченным выборкам. Так могут быть получены выборочная медиана, среднее арифметическое трех или пяти порядковых статистик.
Известна простая и довольно точная оценка математического ожидания — среднее арифметическое двух «наилучших» порядковых статистик, симметрично расположенных относительно медианы:

где  целая часть числа.
целая часть числа.
Оценка, усредняющая все наблюдения, кроме двух крайних  в (13)), имеет вид:
в (13)), имеет вид:

Далее, коэффициенты  могут быть постоянными и зависеть от номера
могут быть постоянными и зависеть от номера  положения наблюдения в вариационном ряду. Так, существует формула
положения наблюдения в вариационном ряду. Так, существует формула

Функция  непрерывна и определена на отрезке
непрерывна и определена на отрезке  Она определяется законом распределения
Она определяется законом распределения  и критерием оценивания. Так, для нормального закона и среднеквадратичного критерия точности При оценивании по усеченной выборке для
и критерием оценивания. Так, для нормального закона и среднеквадратичного критерия точности При оценивании по усеченной выборке для  оценка имеет вид:
оценка имеет вид:

Как отразилось усечение выборки на точности оценки? Дисперсия этой оценки равна  , а оптимальная оценка по полной выборке
, а оптимальная оценка по полной выборке  имеет дисперсию, равную
имеет дисперсию, равную  Таков проигрыш в точности. Выигрыш может быть получен в надежности результата и определяется тем, насколько справедливы сомнения относительно достоверности отброшенных крайних. Если эти сомнения несправедливы, проигрыш в точности ничем не компенсирован.
Таков проигрыш в точности. Выигрыш может быть получен в надежности результата и определяется тем, насколько справедливы сомнения относительно достоверности отброшенных крайних. Если эти сомнения несправедливы, проигрыш в точности ничем не компенсирован.
Отметим любопытный факт. Линейная по отношению к ранжированной выборке Операция  порядковыми статистиками соответствует нелинейному преобразованию над исходной (неупорядоченной) выборкой
порядковыми статистиками соответствует нелинейному преобразованию над исходной (неупорядоченной) выборкой

поскольку уже сама операция упорядочивания выборки нелинейна.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
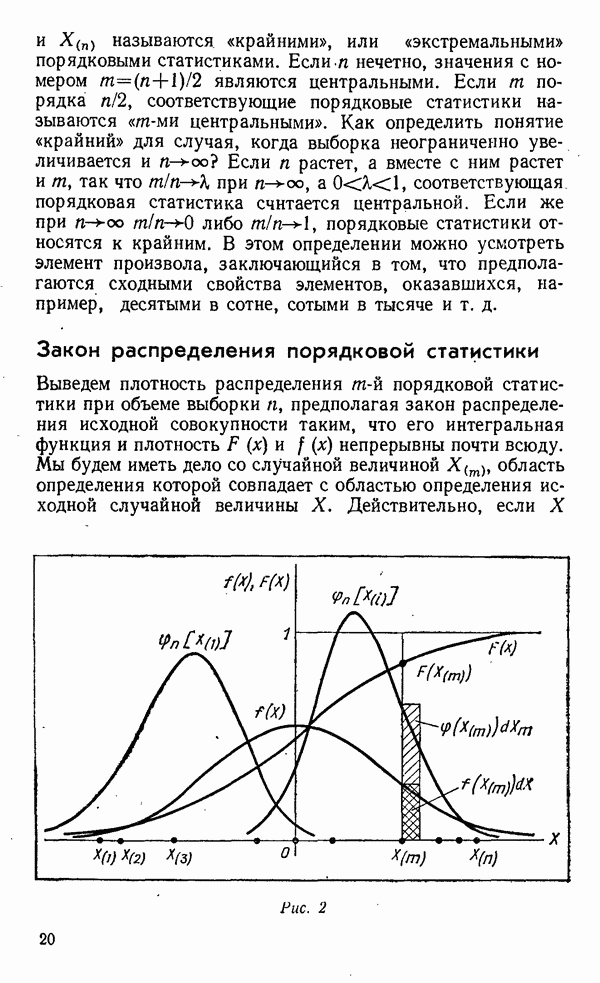
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
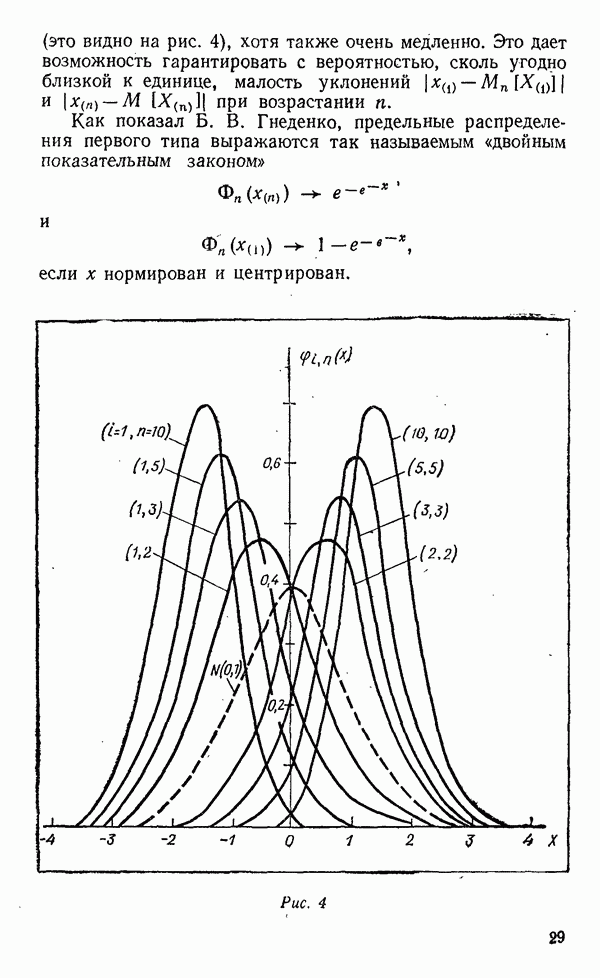
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
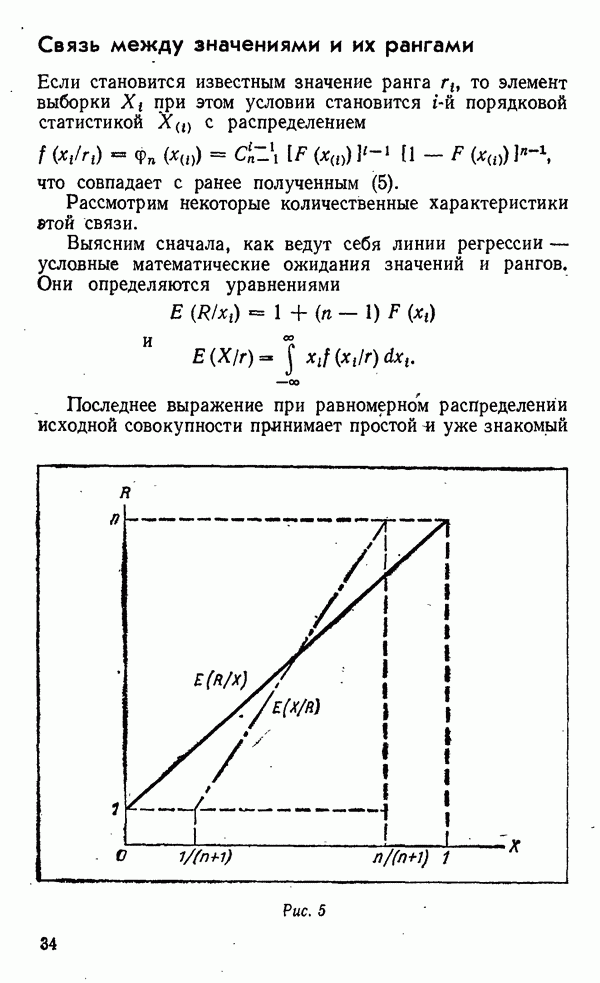
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
- Идентификация объекта с ненаблюдаемым входом
- Безэталонная классификация
- ЛИТЕРАТУРА