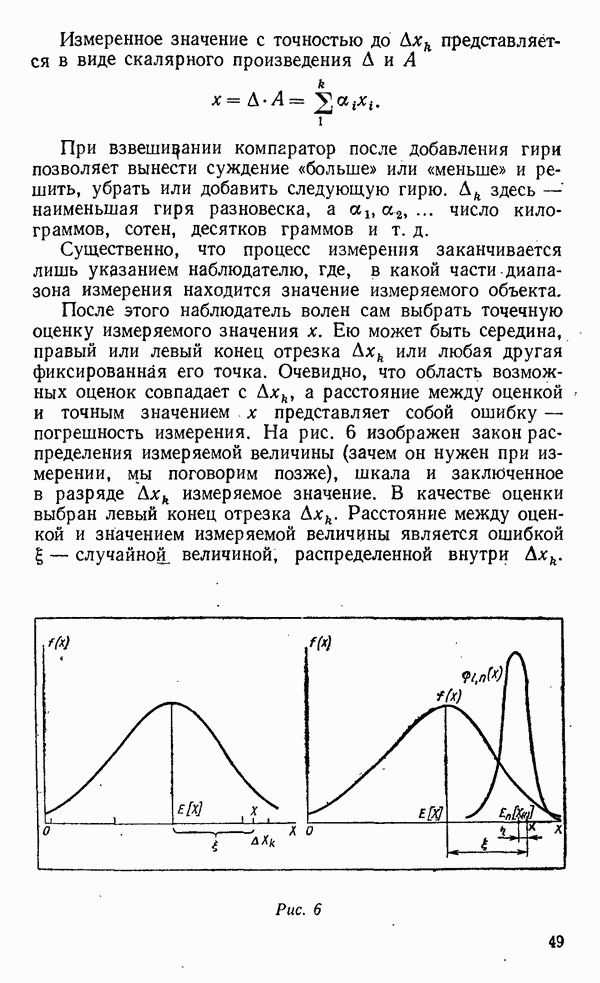
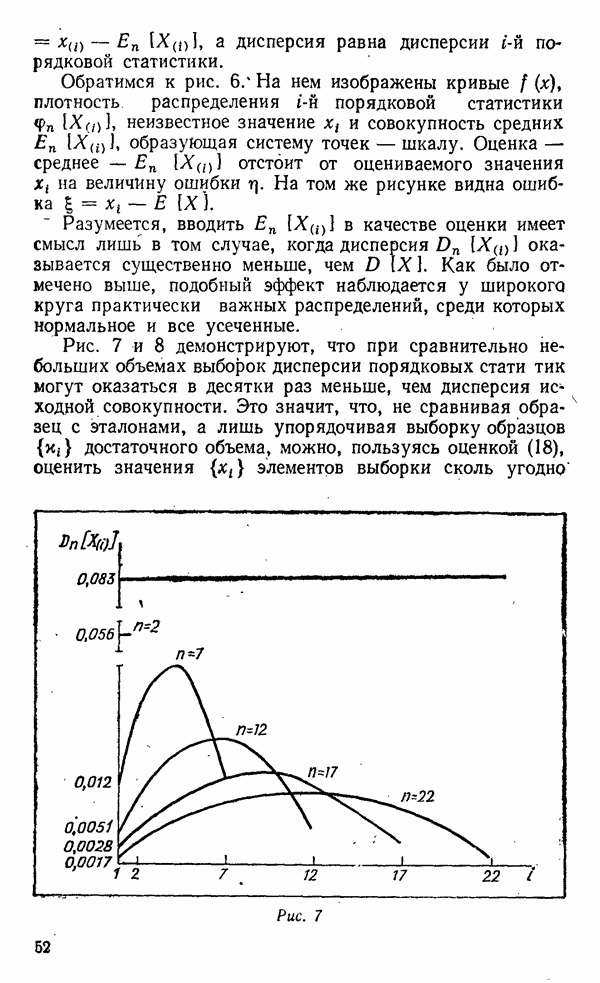
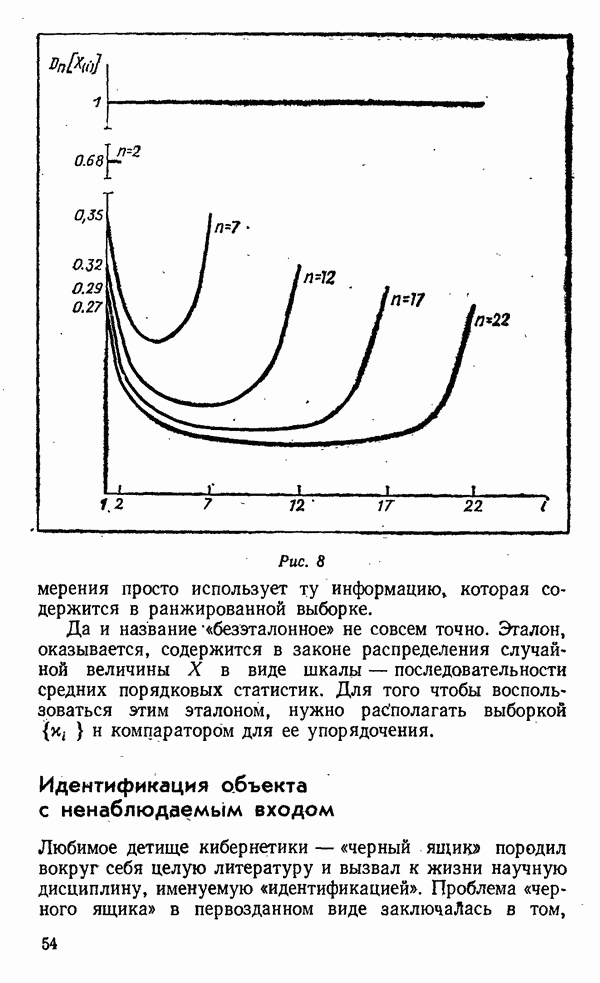
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Идентификация объекта с ненаблюдаемым входом
Любимое детище кибернетики — «черный ящик» породил вокруг себя целую литературу и вызвал к жизни научную дисциплину, именуемую «идентификацией». Проблема «черного ящика» в первозданном виде заключалась в том,
чтобы, подавая на вход некоторого объекта пробные сигналы и наблюдая его реакцию — сигналы на выходе, определить структуру и параметры объекта, узнать, что в «ящике».
Десятилетия изучения проблемы 111] позволили охватить широкий класс идентифицируемых объектов, свести к минимуму необходимую информацию, но оставили в неприкосновенности главный принцип — принцип наблюдаемости входа и выхода.
Между тем рассмотренная выше оценка выборочных значений (18) позволяет поставить новую задачу идентификации: определение неизвестной статической (безынерционной) характеристики звена с ненаблюдаемым входом [10].
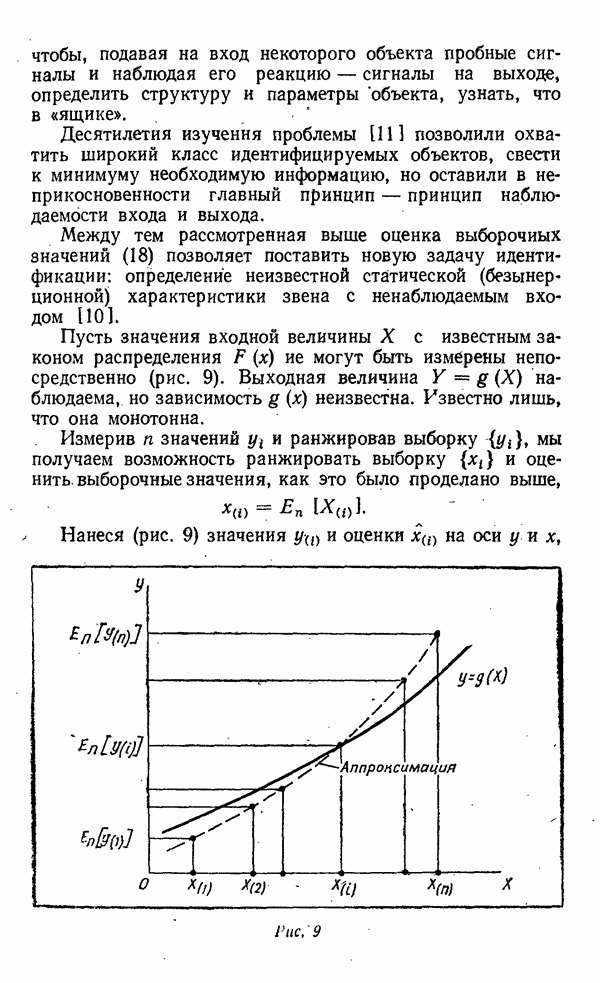
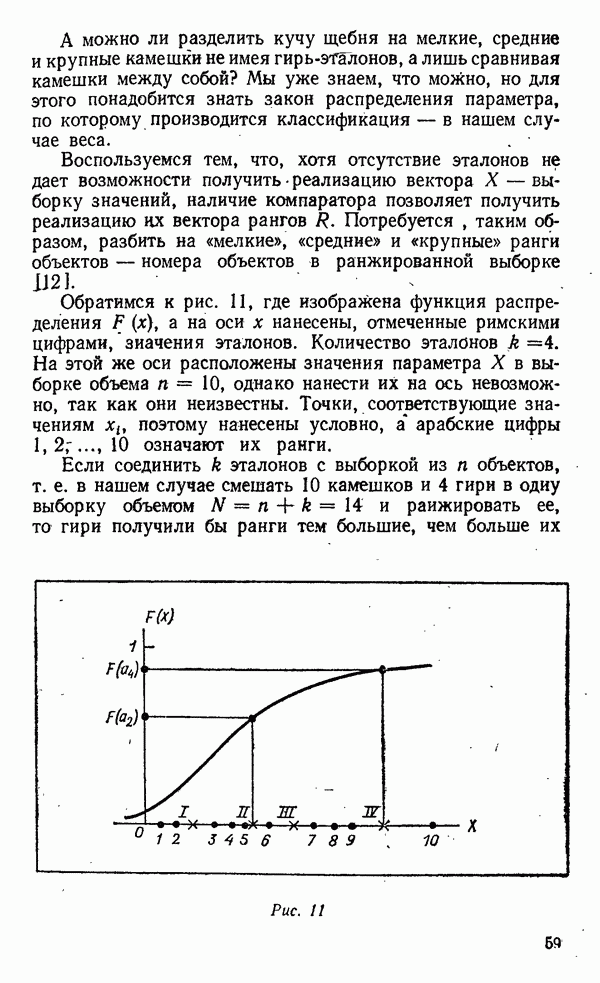
Пусть значения входной величины X с известным законом распределения  не могут быть измерены непосредственно (рис. 9). Выходная величина
не могут быть измерены непосредственно (рис. 9). Выходная величина  наблюдаема, но зависимость
наблюдаема, но зависимость  неизвестна. Известно лишь, что она монотонна.
неизвестна. Известно лишь, что она монотонна.
Измерив  значений
значений  и ранжировав выборку
и ранжировав выборку  мы получаем возможность ранжировать выборку
мы получаем возможность ранжировать выборку  и оценить, выборочные значения, как это было проделано выше,
и оценить, выборочные значения, как это было проделано выше,

Нанеся (рис. 9) значения  и оценки
и оценки  на оси у и х,
на оси у и х,

Рис. 9.
мы сможем тем, или иным способом установить (идентифицировать) зависимость  Проделаем это с помощью метода наименьших квадратов, несколько конкретизировав задачу.
Проделаем это с помощью метода наименьших квадратов, несколько конкретизировав задачу.
Предположим, что зависимость  параметризована, линейна по параметрам и имеет вид:
параметризована, линейна по параметрам и имеет вид:

где  известная функция,
известная функция,  параметры, которые следует найти. Тогда, имея набор упорядоченных наблюдений
параметры, которые следует найти. Тогда, имея набор упорядоченных наблюдений  получаем
получаем 
В этом случае математическое ожидание фактических наблюдений  представляет собой линейные функции искомых параметров и
представляет собой линейные функции искомых параметров и 

Ковариации наблюдений известны с точностью до постоянного множителя Ф?

Нам предстоит найти оценки и неизвестных параметров и 
Напомним, что метод наименьших квадратов требует некоррелированности наблюдений. Это требование, как мы видим, не выполняется — упорядочивание превращает элементы выборки в коррелированные случайные величины. Для преодоления трудности такого рода разработан «обобщенный метод», позволивший обрабатывать коррелированные последовательности.
Выражения для оценок  определяются из системы нормальных уравнений обобщенным методом наименьших квадратов
определяются из системы нормальных уравнений обобщенным методом наименьших квадратов 
Не приводя вывода, дадим окончательные выражения для оценок  и
и  :
:

Оценки определяются лишь крайними элементами выборки. Операция ранжирования в этом случае не нужна, достаточно выбрать наибольший и наименьший элементы.
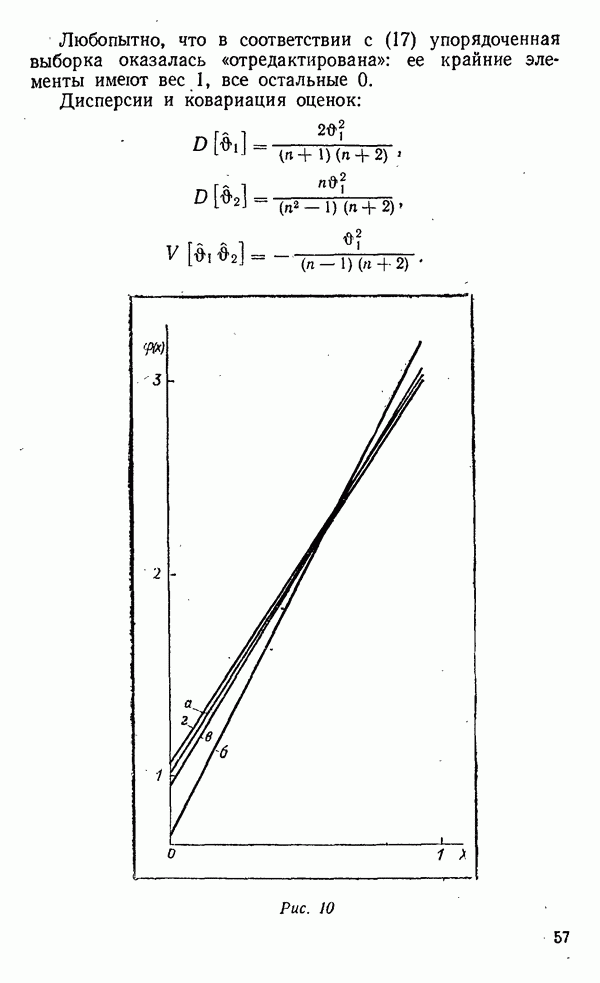
Любопытно, что в соответствии с (17) упорядоченная выборка оказалась «отредактирована»: ее крайние элементы имеют вес 1, все остальные 0.
Дисперсии и ковариация оценок:


Рис. 10
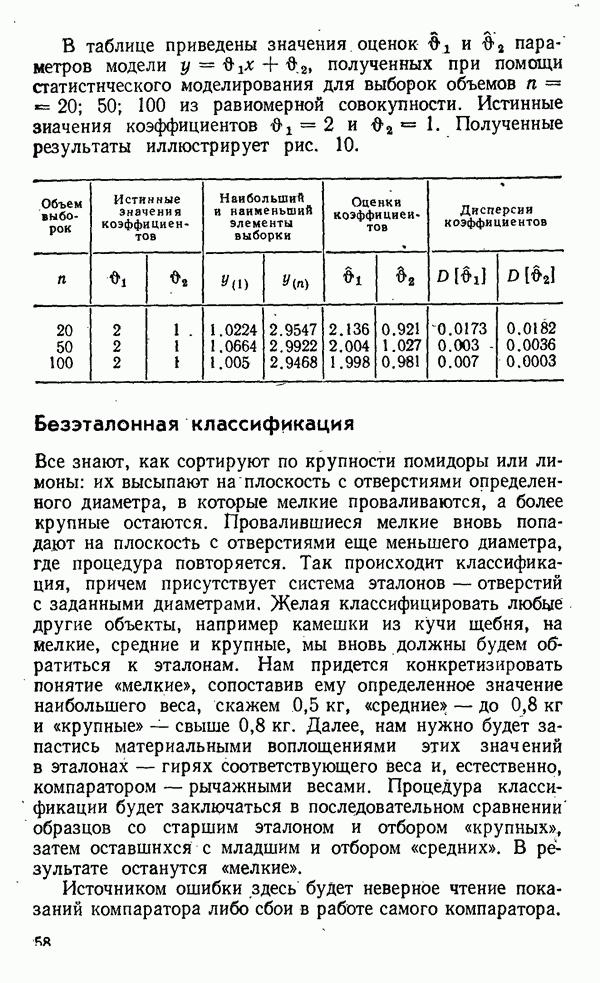
В таблице приведены значения оценок  и параметров модели
и параметров модели  полученных при помощи статистического моделирования для выборок объемов
полученных при помощи статистического моделирования для выборок объемов  из равномерной совокупности. Истинные значения коэффициентов
из равномерной совокупности. Истинные значения коэффициентов  Полученные результаты иллюстрирует рис. 10.
Полученные результаты иллюстрирует рис. 10.

| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
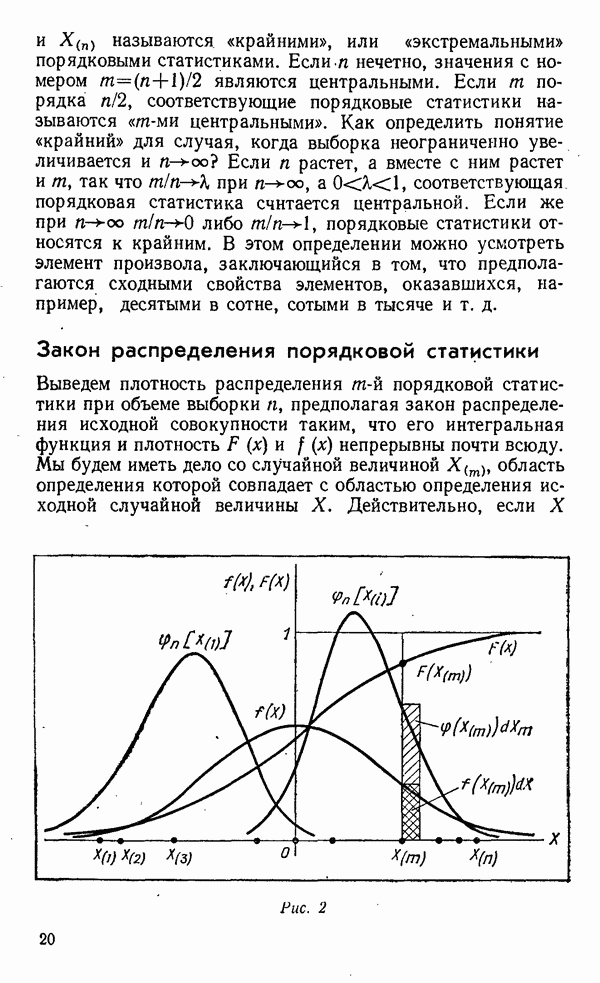
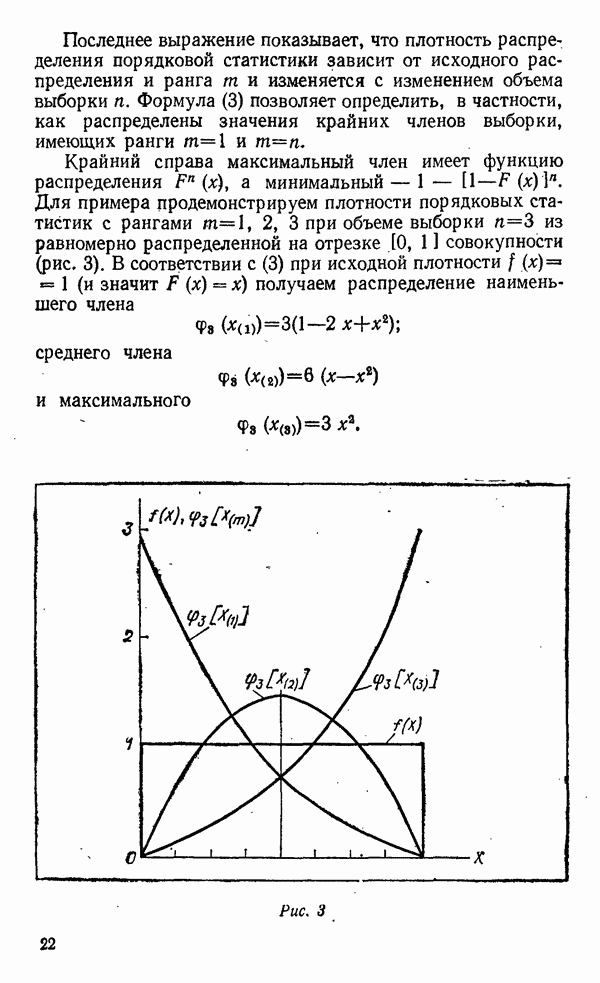
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
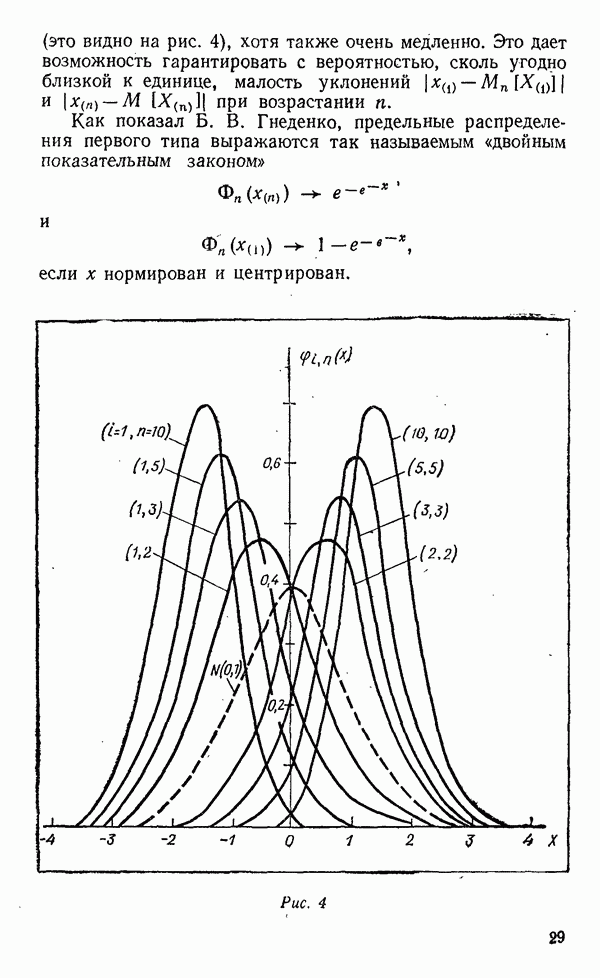
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
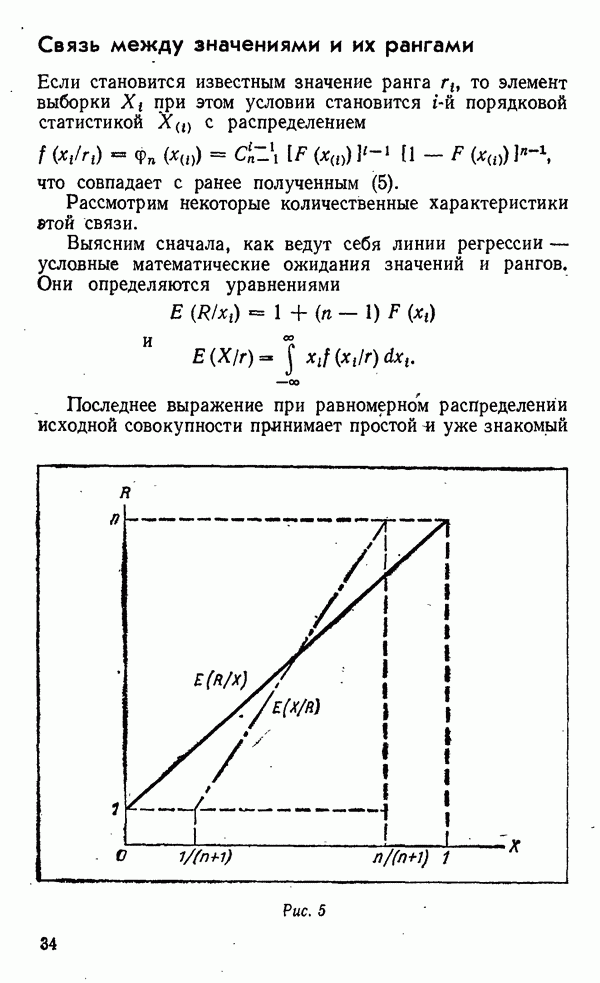
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
- Идентификация объекта с ненаблюдаемым входом
- Безэталонная классификация
- ЛИТЕРАТУРА