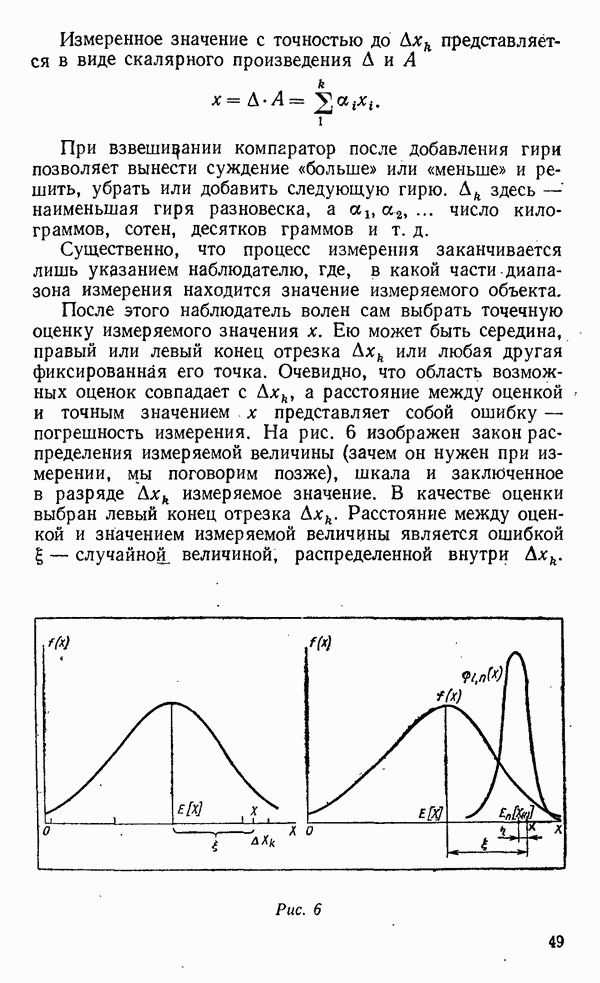
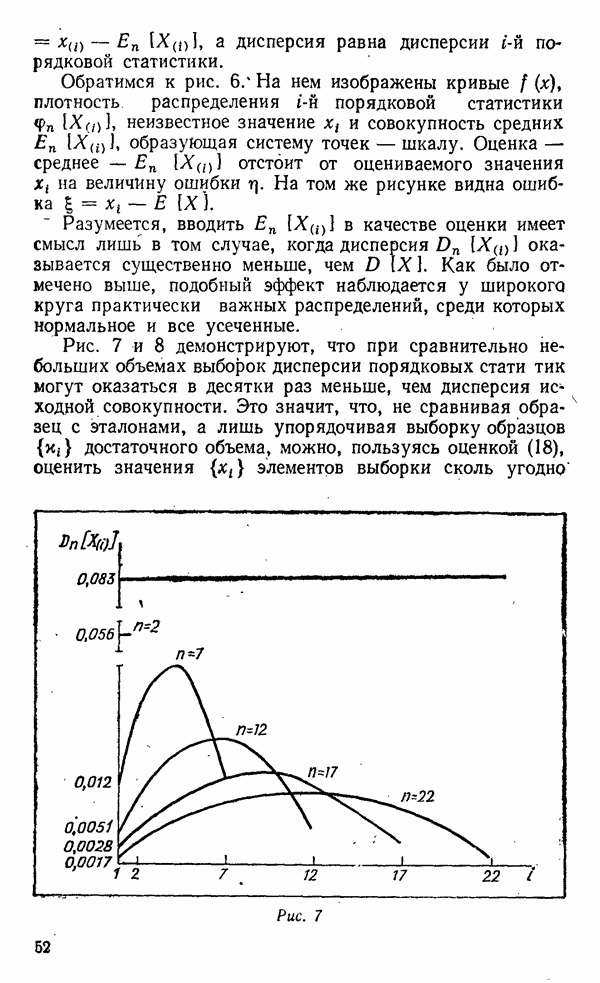
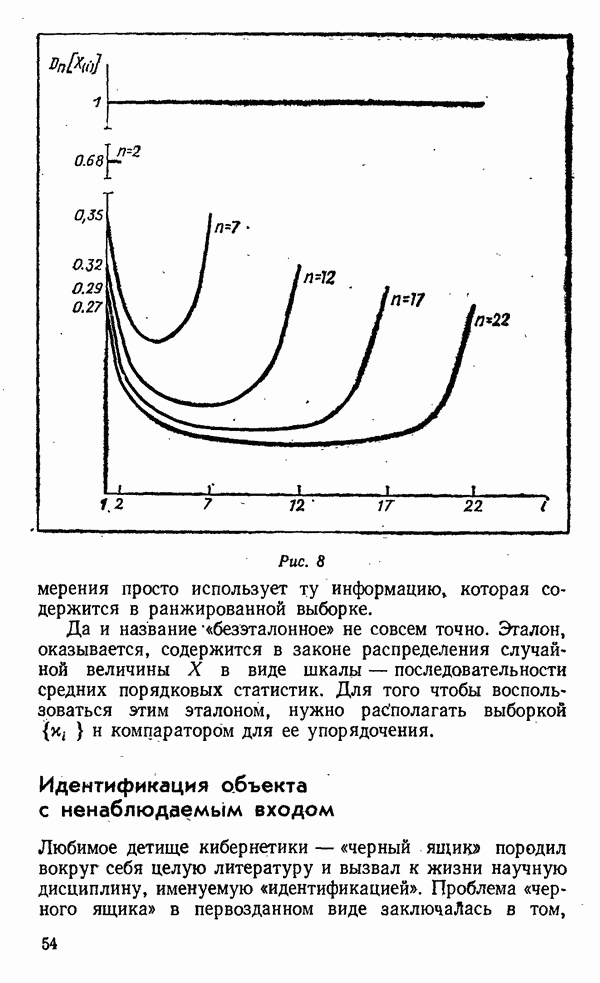
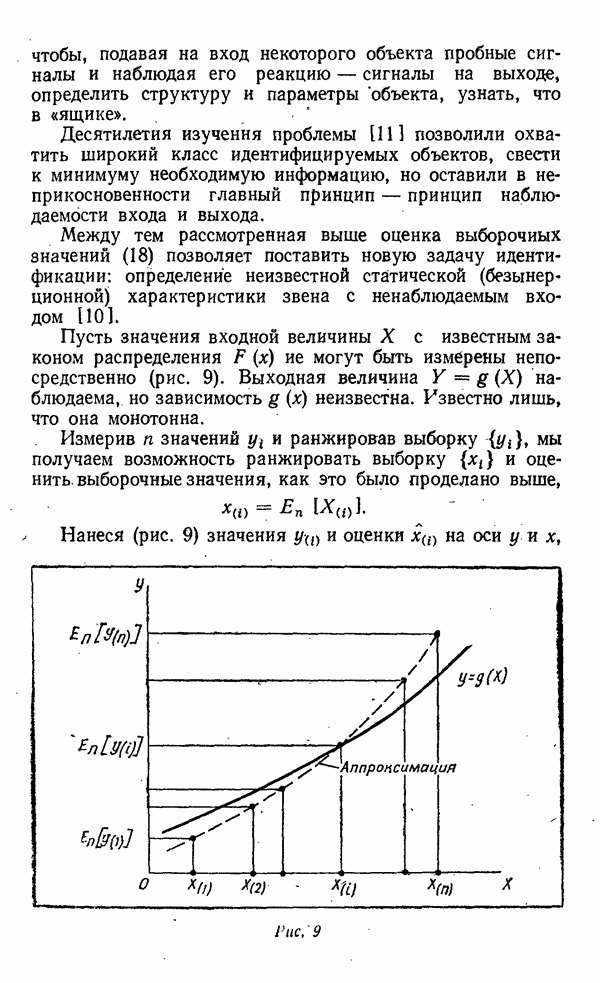
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Распределения крайних значений
Крайние члены выборки представляют большой интерес, поскольку они зачастую играют в группе особую роль. Так, сколько бы раз мы ни растягивали цепь, разорвавшееся звено — крайнее слева в прочностном ряду звеньев. Забеги и заплывы на соревнованиях выделяют сильнейших, которые соревнуются между собой на следующих этапах соревнований. Есть такие экзотические виды спорта, где зачет идет по слабейшему члену команды и побеждает та, которая обзавелась «лучшим худшим».
Рассмотрим вероятностные свойства крайних. Они оказываются весьма интересными.
Если образована выборка объема  то вероятность, что все ее элементы окажутся меньше определенного значения х, очевидно, равна
то вероятность, что все ее элементы окажутся меньше определенного значения х, очевидно, равна  Вероятность
Вероятность  того, что наибольший элемент этой выборки окажется меньше того же значения х, такая же
того, что наибольший элемент этой выборки окажется меньше того же значения х, такая же

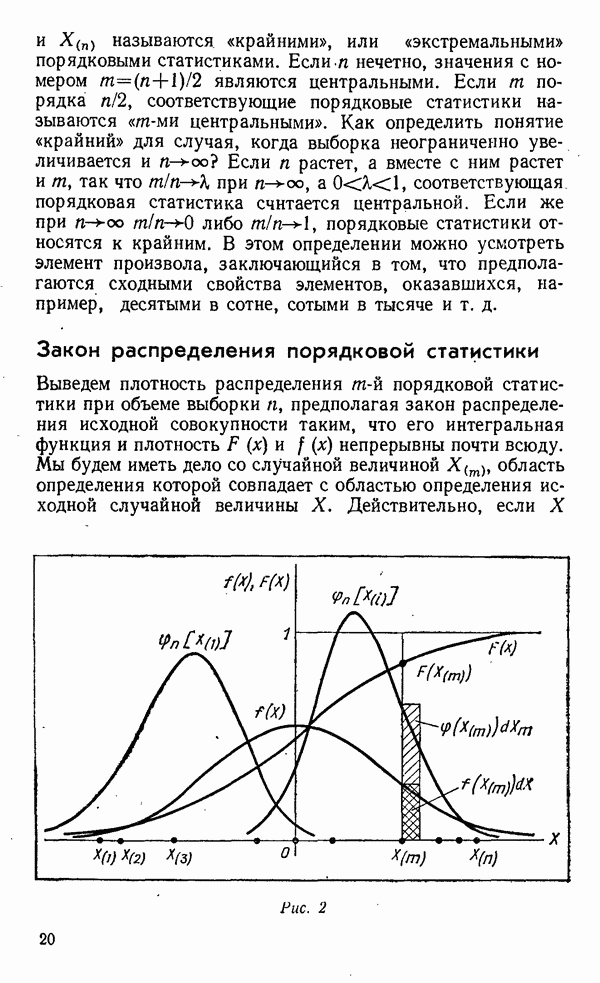
Напомним, что наибольшая наблюдаемая величина в выборке не фиксированное значение, а самостоятельная случайная величина. Свойства функции  зависят от характера закона распределения
зависят от характера закона распределения  в основном в области больших значений х, а так как
в основном в области больших значений х, а так как  велико именно в больших выборках, то, значит, при
велико именно в больших выборках, то, значит, при  Если
Если  заданы тем или иным способом, то
заданы тем или иным способом, то  тем самым уже установлена. При увеличении
тем самым уже установлена. При увеличении  сдвигается вправо и, как оказывается, стремится к асимптотической форме.
сдвигается вправо и, как оказывается, стремится к асимптотической форме.
Рассуждения, аналогичные тем, что привели к (2), позволяют получить вероятность того, что наименьшее значение превзойдет 

Выражения (6) и (7) определяют и функции плотности:

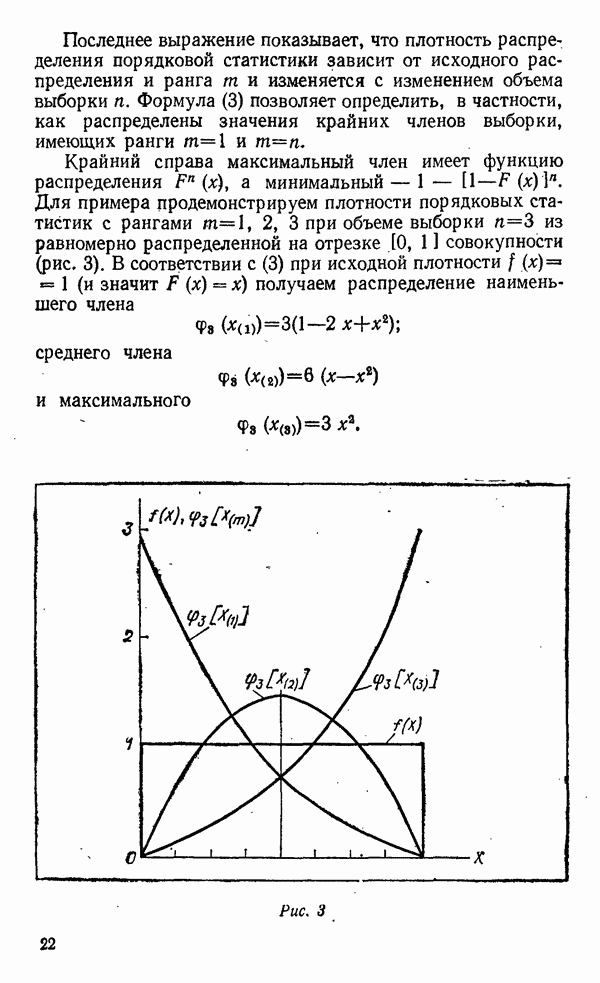
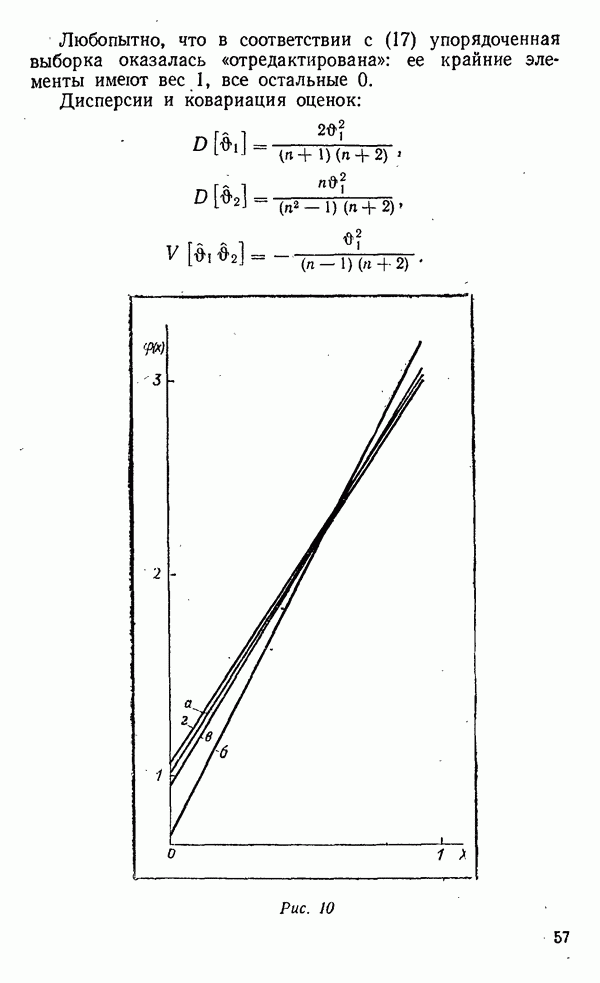
Если плотность исходной. совокупности симметрична, наибольшее и наименьшее значения распределены взаимно симметрично:  так что, располагая распределением наибольшего, можно найти распределение наименьшего значения. Наш пример с равномерным распределением (рис. 3) иллюстрирует это кривыми
так что, располагая распределением наибольшего, можно найти распределение наименьшего значения. Наш пример с равномерным распределением (рис. 3) иллюстрирует это кривыми  и
и
 позволяет исследование экстремальных значений свести к исследованию только наибольшего. Если исходное распределение симметрично относительно нуля, вероятность, что наибольшее значение будет положительным, быстро приближается к единице при увеличении объема выборки.
позволяет исследование экстремальных значений свести к исследованию только наибольшего. Если исходное распределение симметрично относительно нуля, вероятность, что наибольшее значение будет положительным, быстро приближается к единице при увеличении объема выборки.
Закон распределения наибольшего значения (6) можно представить в виде  и проследить за изменением
и проследить за изменением  При больших
При больших  значение
значение  приближается к единице, а показатель экспоненты превращается в неопределенность типа
приближается к единице, а показатель экспоненты превращается в неопределенность типа  и, значит,
и, значит,  определяется характером приближения
определяется характером приближения  к единице. Таким образом, существование асимптотических выражений связано с некоторыми условиями, накладываемыми на исходное распределение при больших значениях.
к единице. Таким образом, существование асимптотических выражений связано с некоторыми условиями, накладываемыми на исходное распределение при больших значениях.
При анализе экстремальных значений вводят новую характеристику крайних: период повторяемости. Если считать, что наблюдения проводятся через равные промежутки времени, число наблюдений приобретает размерность времени, а выражение

называется периодом повторяемости значения, большего или равного х. Период повторяемости представляет собой ожидаемое число наблюдений, после которых появится одно значение, превосходящее х. Функция  удовлетворяет условию
удовлетворяет условию

Период повторяемости неограниченно растет с ростом х.
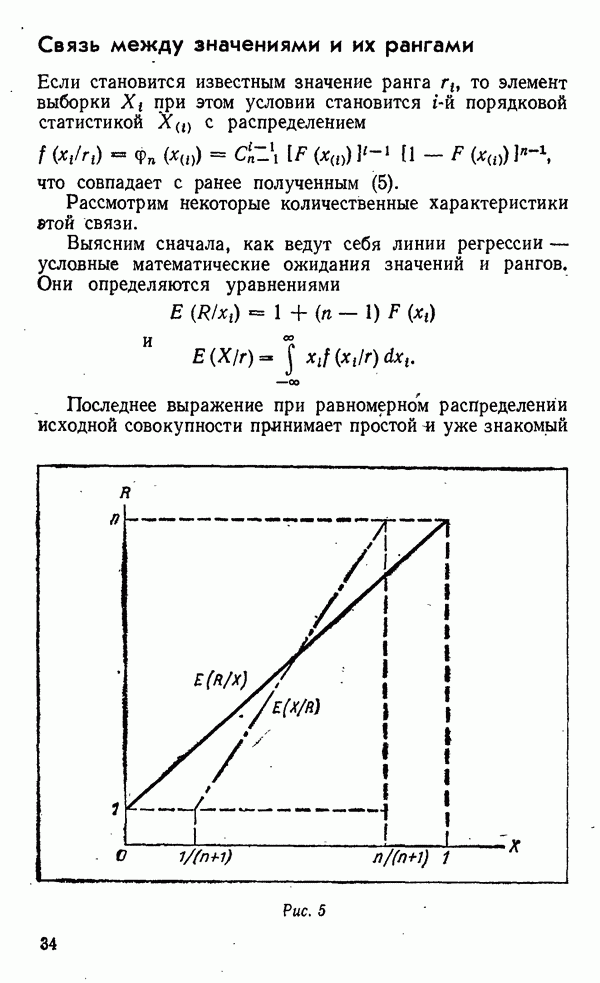
С периодом повторяемости связаны «характеристические» Наибольшее и наименьшее значения

Они представляют собой квантили исходного распределения

По определению ожидаемое число больших  или меньших значений равно единице. С ростом
или меньших значений равно единице. С ростом  растет,
растет,  убывает. Для симметричных распределений
убывает. Для симметричных распределений

Еще одна статистическая функция, важная для анализа экстремальных значений, называемая интенсивностью, определяется выражением

и для характеристических экстремальных значений равна

Эти величины называют экстремальными интенсивностями. С ростом  функции интенсивности, в зависимости от вида закона распределения, ведет себя по-разному: может возрастать, оставаться постоянной или убывать.
функции интенсивности, в зависимости от вида закона распределения, ведет себя по-разному: может возрастать, оставаться постоянной или убывать.
Установлено, что существуют всего три типа асимптотических распределений крайних. Все возможные исходные распределения классифицируются по тому, к распределению какого типа принадлежат их крайние.
К распределению первого типа приводят такие неограниченные исходные, у которых  -вероятность, что значение превзойдет х, сходится к нулю не медленнее, чем
-вероятность, что значение превзойдет х, сходится к нулю не медленнее, чем  . К этой категории принадлежит большинство применяемых на практике распределений — нормальное, экспоненциальное, логарифмически нормальное, логистическое и гамма-распределение.
. К этой категории принадлежит большинство применяемых на практике распределений — нормальное, экспоненциальное, логарифмически нормальное, логистическое и гамма-распределение.
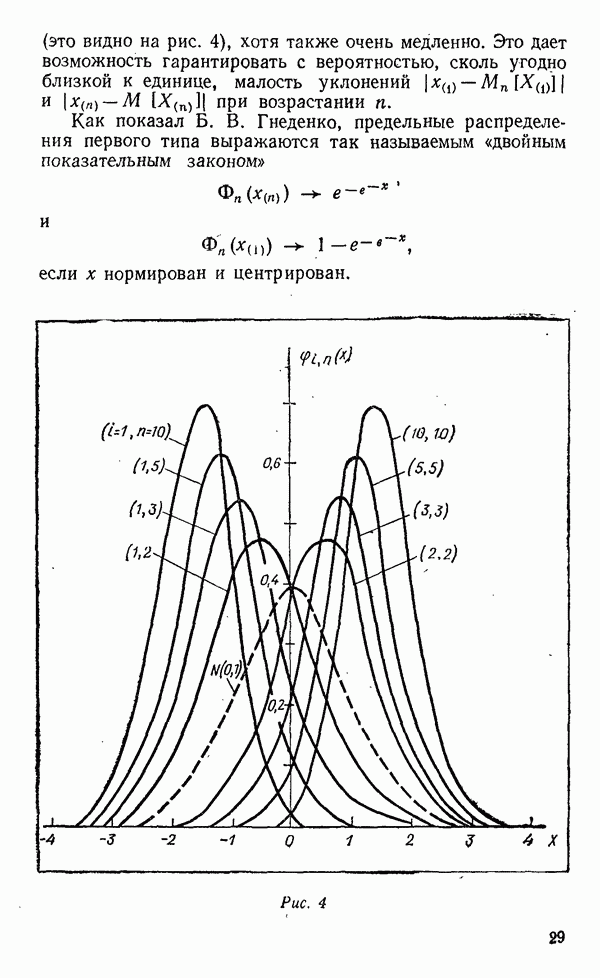
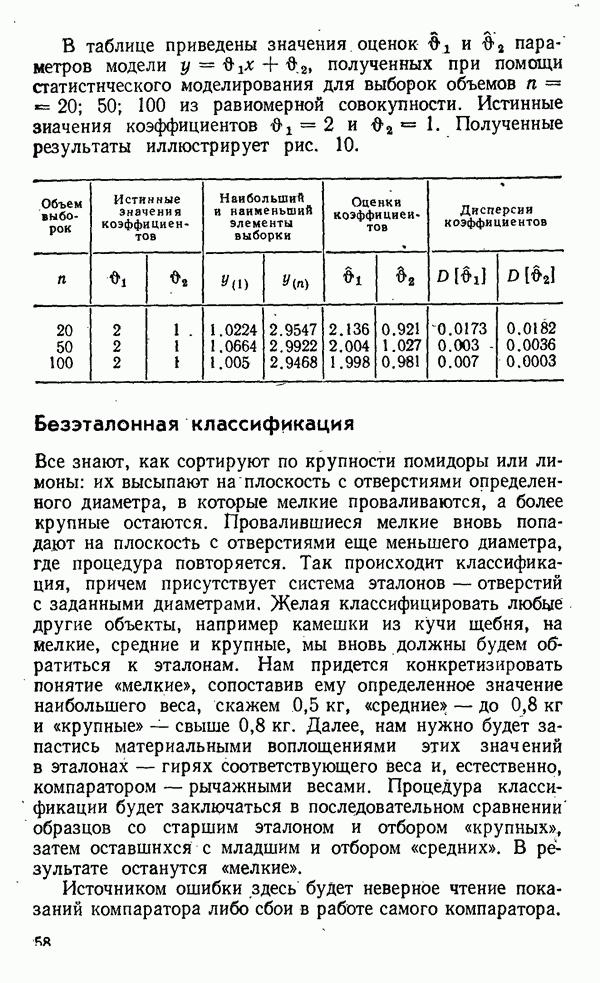
На рис. 4 изображены плотности распределения крайних членов из выборки с нормальным исходным распределением при  Таков же характер изменения плотности крайних и для других законов, приводящих к распределению первого типа. Мы видим, что с увеличением
Таков же характер изменения плотности крайних и для других законов, приводящих к распределению первого типа. Мы видим, что с увеличением  распределение все более тесно концентрируется относительно среднего, в свою очередь неограниченно возрастающего вместе с объемом выборки. Рост крайних происходит медленно, но известно, что при
распределение все более тесно концентрируется относительно среднего, в свою очередь неограниченно возрастающего вместе с объемом выборки. Рост крайних происходит медленно, но известно, что при  максимальный член с вероятностью единица превзойдет любое наперед заданное число. Математическое ожидание крайних чледов будет приближенно выражаться следующим равенством:
максимальный член с вероятностью единица превзойдет любое наперед заданное число. Математическое ожидание крайних чледов будет приближенно выражаться следующим равенством:

Таким образом, «раздвигание границ» выборочного распределения с возрастанием объема выборки происходит крайне медленно, пропорционально  при этом дисперсия крайних членов с ростом
при этом дисперсия крайних членов с ростом  может стремиться к нулю
может стремиться к нулю
(это видно на рис. 4), хотя также очень медленно. Это дает возможность гарантировать с вероятностью, сколь угодно близкой к единице, малость уклонений  при возрастании
при возрастании 
Как показал Б. В. Гнеденко, предельные распределения первого типа выражаются так называемым «двойным показательным законом»

и

если х нормирован и центрирован.
Рис. 4 (см. скан)
Дисперсия наибольшего значения при этом имеет простой вид:

где  экстремальная интенсивность.
экстремальная интенсивность.
Экстремальная интенсивность с ростом  может возрастать, а дисперсия стремиться к нулю (нормальное распределение), оставаться постоянной, как и дисперсия (экспоненциальное и логистическое распределения), или убывать, что влечет за собой рост дисперсии (логарифмически нормальное распределение).
может возрастать, а дисперсия стремиться к нулю (нормальное распределение), оставаться постоянной, как и дисперсия (экспоненциальное и логистическое распределения), или убывать, что влечет за собой рост дисперсии (логарифмически нормальное распределение).
К распределению крайних третьего типа приводят ограниченные исходные распределения. Если распределение ограничено справа,  при
при  (тогда как при
(тогда как при  то при достаточно больших
то при достаточно больших  возможные значения максимального члена будут в основном сконцентрированы в соседстве с точкой
возможные значения максимального члена будут в основном сконцентрированы в соседстве с точкой  в интервале
в интервале  при любом
при любом 
На рис. 3 изображены распределения крайних выборок  из исходной совокупности, подчиненной равномерному распределению. Видно, как кривые плотностей с ростом
из исходной совокупности, подчиненной равномерному распределению. Видно, как кривые плотностей с ростом  приближаются к границам распределения. Дисперсия с ростом
приближаются к границам распределения. Дисперсия с ростом  неограниченно уменьшается.
неограниченно уменьшается.
Асимптотическое распределение имеет вид:

где  нормированное расстояние до границы
нормированное расстояние до границы  а
а 
Существуют распределения, ограниченные с одной стороны и не ограниченные с другой. Так, например, показательное распределение, распределение Рэлея ограничены слева, но не ограничены справа. В выборках из таких исходных совокупностей распределение максимальных значений будет относиться к первому асимптотическому типу, а минимальных — к третьему.
К распределению крайних второго типа приводят неограниченные исходные распределения, плотность которых убывает с ростом  так медленно, что моментов не существует. К таким относятся, например, распределения Коши и Парето. Отметим лишь, что логарифмы наибольших значений, взятых из распределения типа Коши, распределены как наибольшие значения, взятые из распределения экспоненциального типа. Важно также, что с ростом
так медленно, что моментов не существует. К таким относятся, например, распределения Коши и Парето. Отметим лишь, что логарифмы наибольших значений, взятых из распределения типа Коши, распределены как наибольшие значения, взятые из распределения экспоненциального типа. Важно также, что с ростом 
дисперсии крайних не убывают, как в предыдущих случаях, а неограниченно растут.
Вернувшись теперь к нашей модели — куче щебня и ящикам с номерами, по которым раскладывали упорядоченные по весу камни, мы увидим., что если распределение веса камней приводит к распределению крайних I и III типа, то с увеличением  (количество ящиков) весовой состав щебня в них выравнивается — дисперсия убывает. Если бы мы имели дело с распределением II типа, то в ящиках с большими номерами оказались бы очень сильно отличающиеся по весу камни.
(количество ящиков) весовой состав щебня в них выравнивается — дисперсия убывает. Если бы мы имели дело с распределением II типа, то в ящиках с большими номерами оказались бы очень сильно отличающиеся по весу камни.
Статистике крайних посвящена подробная и изустная монография Э. Гумбеля. [6].
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
- Идентификация объекта с ненаблюдаемым входом
- Безэталонная классификация
- ЛИТЕРАТУРА