| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
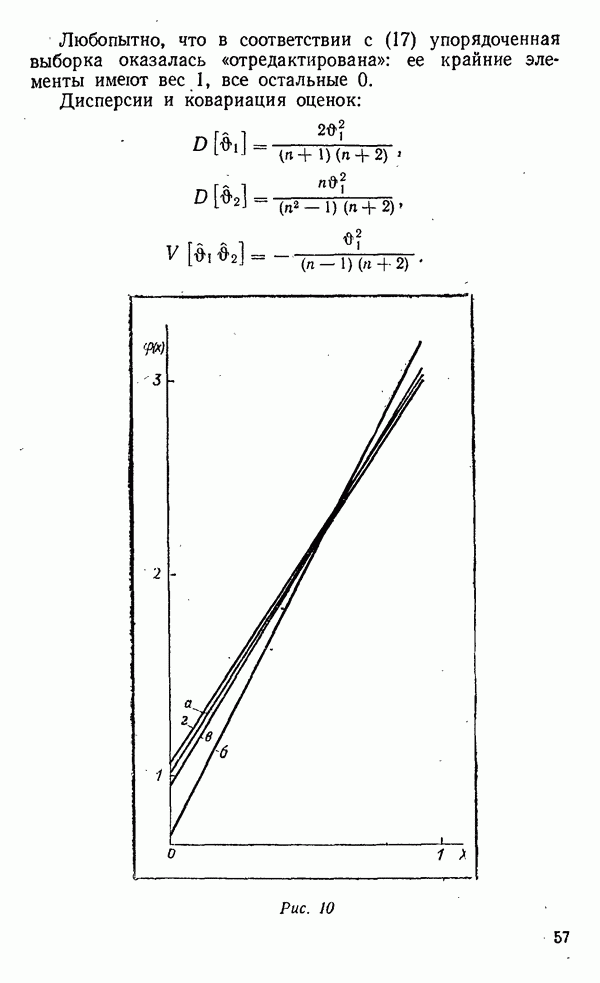
Выборка из трех наблюдений
Изложим, следуя [7], практически важный случай трех наблюдений.
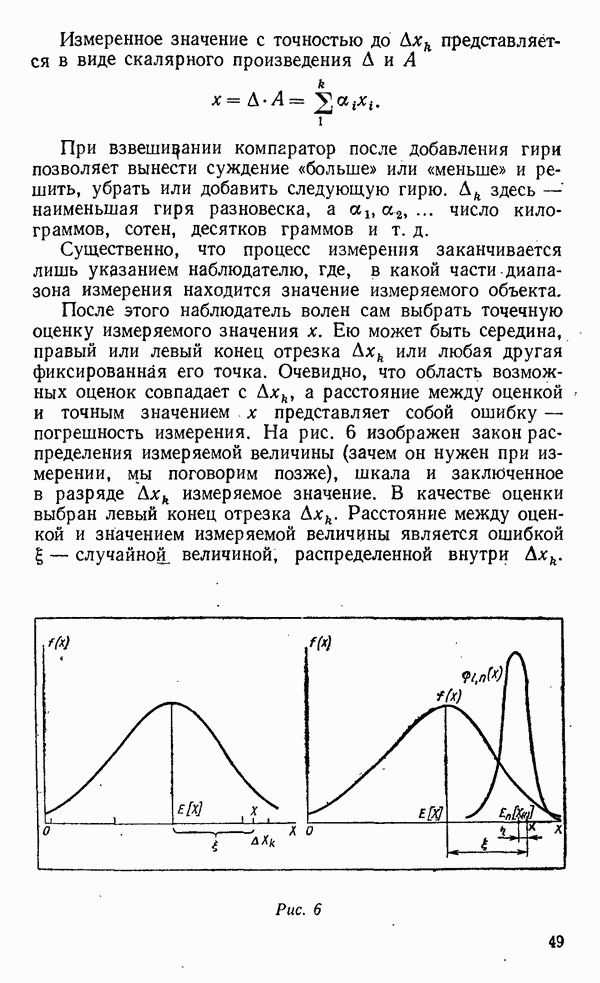
Пусть сделаны три измерения случайной величрны с функцией плотности  Их порядковые статистики
Их порядковые статистики

могут стать основой для вычисления других интересных статистик

которые определяются следующим образом:

Другими словами, наблюдения  лежат ближе друг к другу, а третье
лежат ближе друг к другу, а третье  в стороне от них и может быть наименьшим или наибольшим из всех трех.
в стороне от них и может быть наименьшим или наибольшим из всех трех.
Эти статистики определяются не только своим номером после упорядочения, как порядковые статистики, а представляют собой в некотором смысле их обобщения.
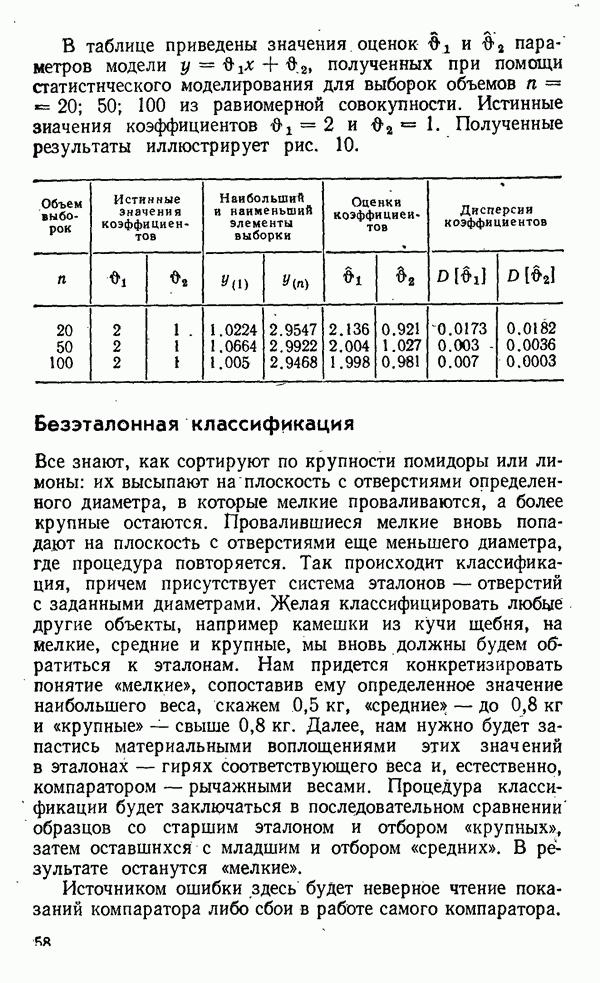
Тройные наблюдения — весьма распространенный в практике экспериментирования прием. Третье измерение иногда делают, чтобы выяснить, какое из первых двух ошибочно. Если при этом два из трех наблюдений хорошо сходятся между собой, у исследователя возникает искушение отвергнуть «отскочившее» третье, как ошиббчное. При этом он полагает, что улучшит результат, если сделает
дополнительное измерение, а худшее отбросит, как если бы его и не было.
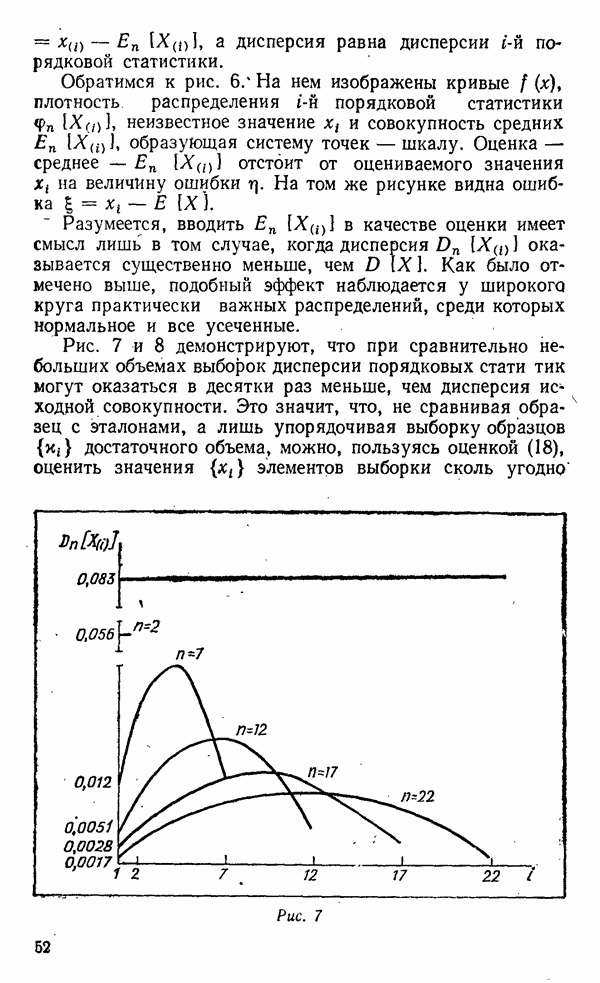
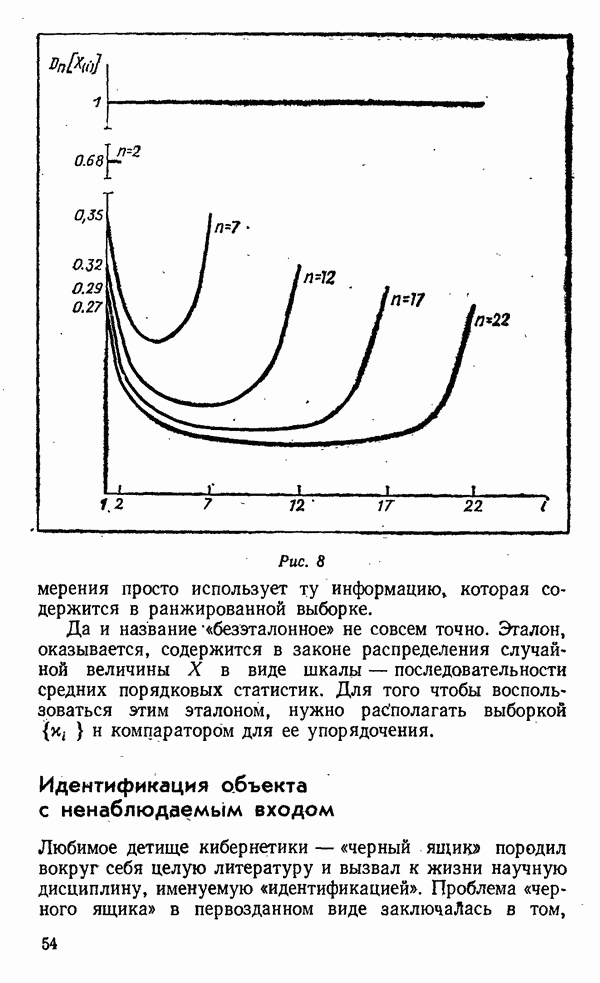
Посмотрим, как влияет такая отбраковка наблюдения на оценки математического ожидания и дисперсии.
Оказывается, что при нормальном и равномерном распределениях пара ближайших друг к другу наблюдений обладает следующими свойствами.
Математическое ожидание разности  составляет менее половины математического ожидания размаха выборки объемом
составляет менее половины математического ожидания размаха выборки объемом  В таком же соотношении находятся среднеквадратичные отклонения этих разностей. Итак, отбрасывание «третьего лишнего» исказило свойство такой важной статистики, как размах. Лучше было бы пользоваться естественной выборкой объема
В таком же соотношении находятся среднеквадратичные отклонения этих разностей. Итак, отбрасывание «третьего лишнего» исказило свойство такой важной статистики, как размах. Лучше было бы пользоваться естественной выборкой объема 
Среднее из двух ближайших  состоятельная оценка математического ожидания, как и среднее из выборки объема
состоятельная оценка математического ожидания, как и среднее из выборки объема  но с несколько большей дисперсией. Особенно интересно, что среднее из двух наиболее расходящихся наблюдений
но с несколько большей дисперсией. Особенно интересно, что среднее из двух наиболее расходящихся наблюдений  служит лучшей оценкой математического ожидания, чем среднее из двух ближайших друг к другу наблюдений.
служит лучшей оценкой математического ожидания, чем среднее из двух ближайших друг к другу наблюдений.
Итак, отбраковка «отскочившего» наблюдения ухудшает свойства и этой статистики.
Это, впрочем, не значит, что отбраковку вообще не следует делать. Отбраковка необходима, если есть основания считать «отскочившее» наблюдение «сорным» — принадлежащим чужому исходному распределению.
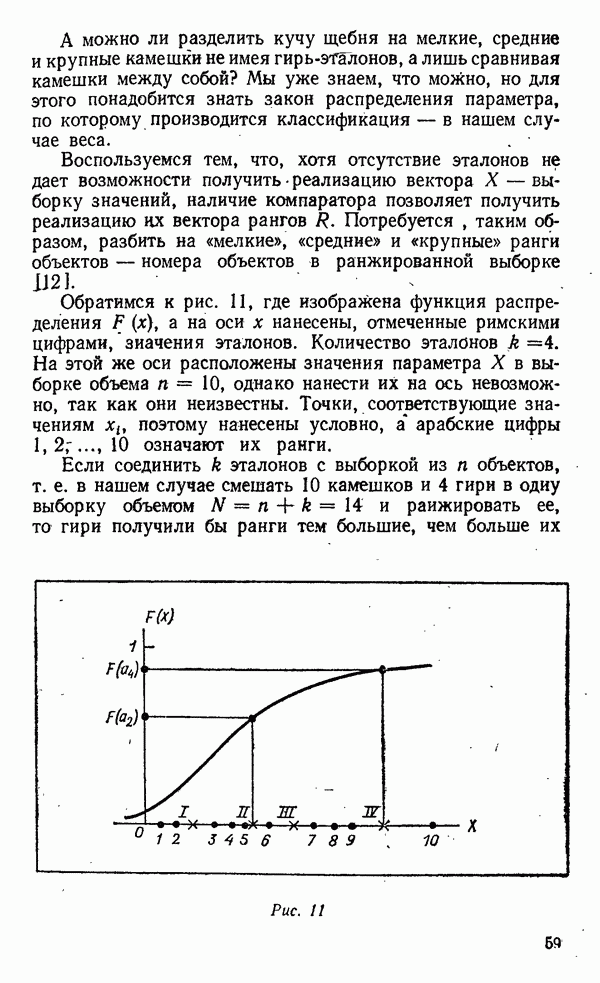
Само по себе «отскочившее» наблюдение  объединяет свойства крайних порядковых статистик
объединяет свойства крайних порядковых статистик  В случае равномерного на
В случае равномерного на  исходного распределения случайная величина
исходного распределения случайная величина  имеет плотность
имеет плотность

равную нормированной сумме плотностей крайних порядковых статистик при  изображенных на рис. 2. Среднее
изображенных на рис. 2. Среднее  т. е. совпадает с
т. е. совпадает с 
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
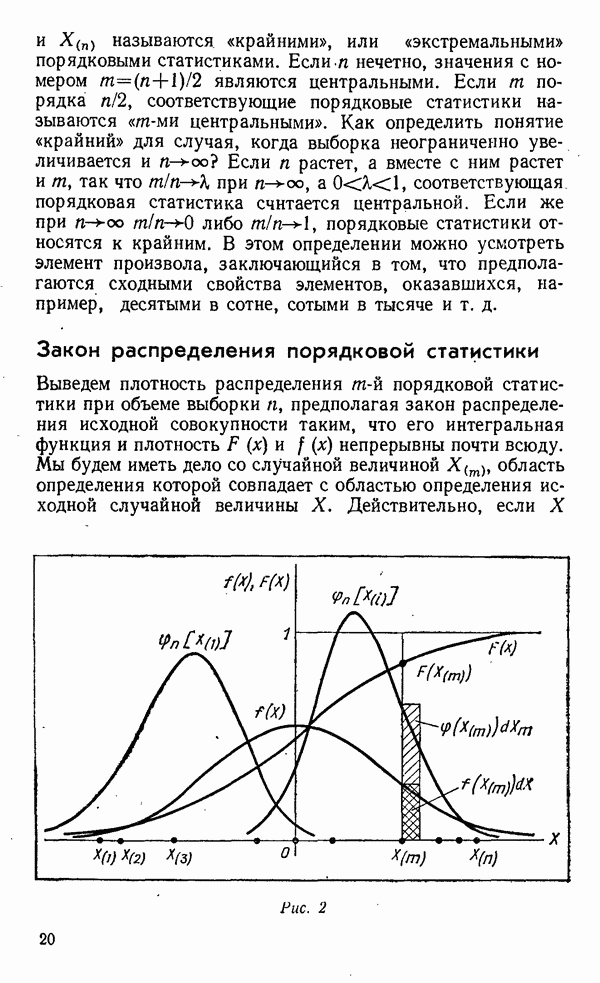
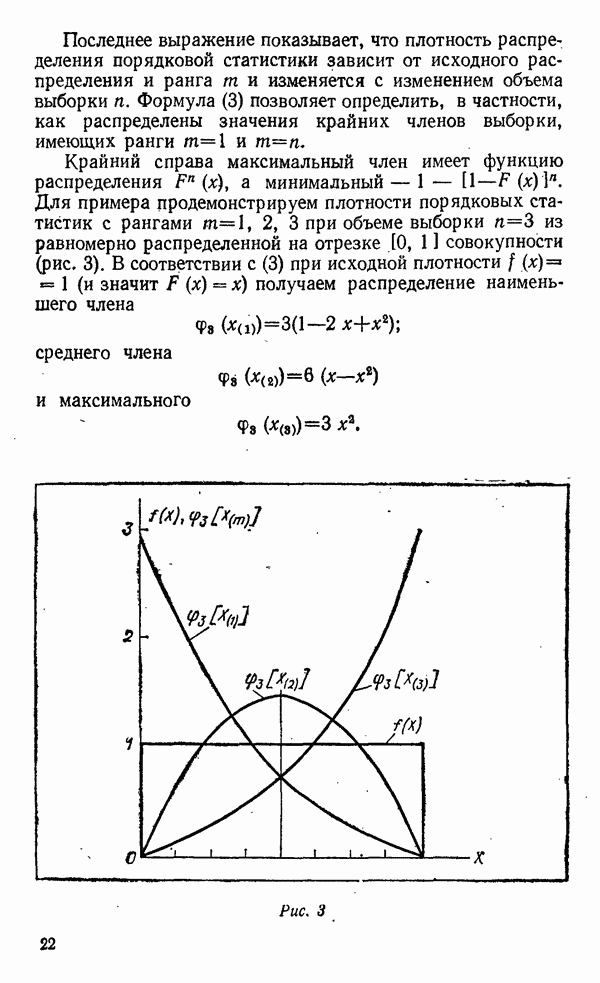
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
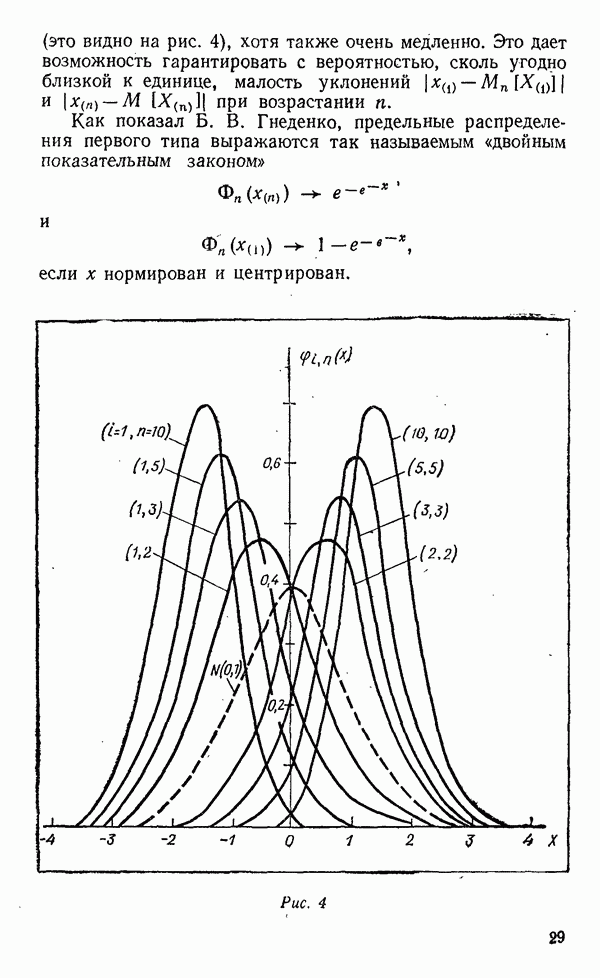
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
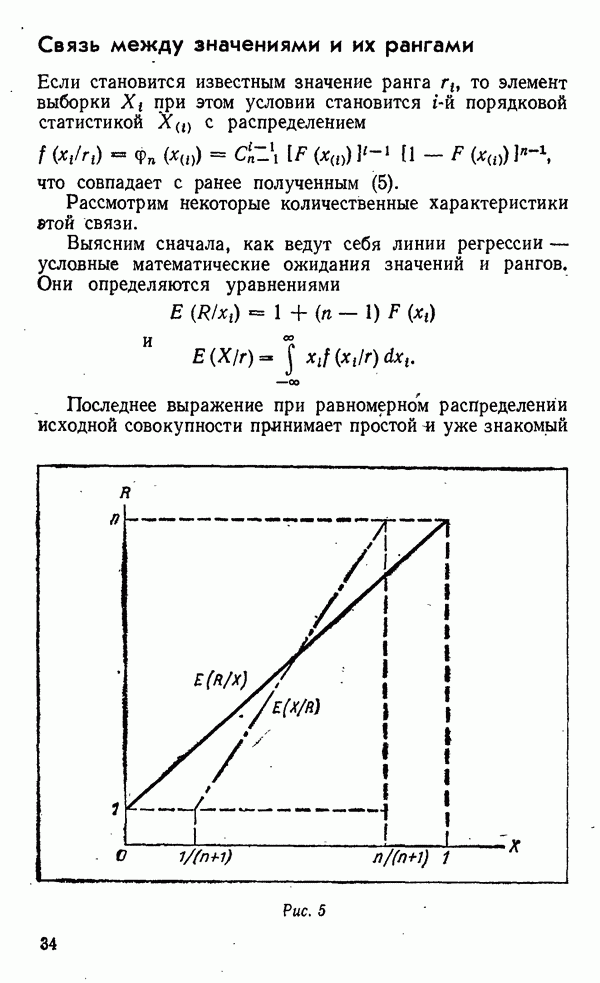
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
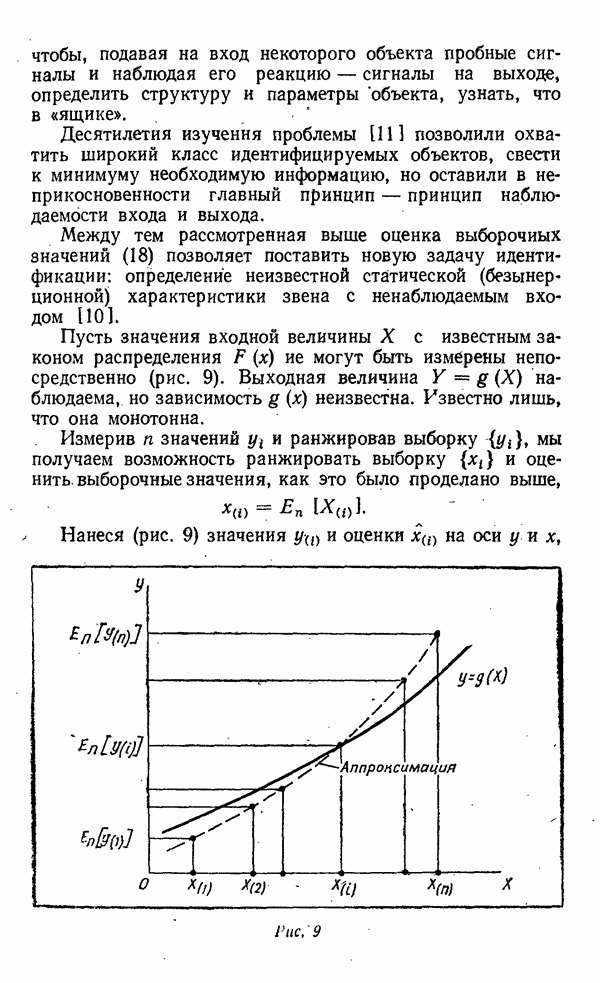
- Идентификация объекта с ненаблюдаемым входом
- Безэталонная классификация
- ЛИТЕРАТУРА