| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Оценки параметров равномерного распределения
Равномерное распределение имеет функцию плотности  где Е — математическое ожидание,
где Е — математическое ожидание,  размах.
размах.
Оценка среднего типа (14) с весовыми коэффициентами для неусеченной выборки имеет вид:

и представляет собой функцию лишь крайних членов выборки. Здесь «усечение» произвел алгоритм выбора весовых коэффициентов, обратив все, кроме крайних, в нули.
Оценка размаха

также зависит лишь от крайних значений. Дисперсия ошибки оценки среднего

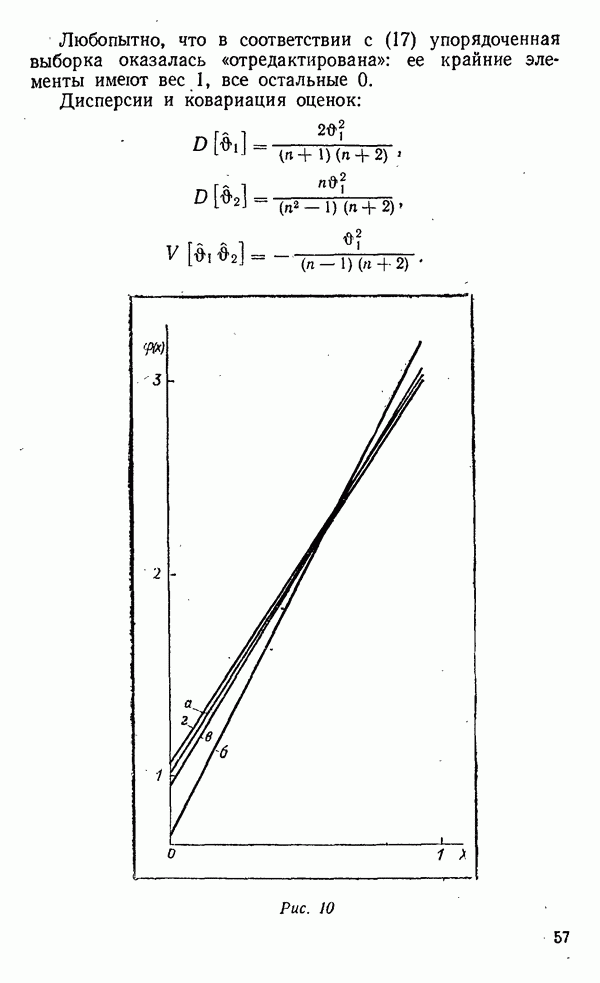
Мы видим, что точность оценки  выше точности выборочного среднего. Напомним, что выборочное среднее — эффективная оценка для математического ожидания нормального распределения. Выражение (17) — нелинейная функция выборки
выше точности выборочного среднего. Напомним, что выборочное среднее — эффективная оценка для математического ожидания нормального распределения. Выражение (17) — нелинейная функция выборки  дающая так называемую «суперэффективную» оценку, оценку, наилучшую среди всех возможных несмещенных оценок.
дающая так называемую «суперэффективную» оценку, оценку, наилучшую среди всех возможных несмещенных оценок.
Если крайние наблюдения приходится отбрасывать  . оценки имеют вид:
. оценки имеют вид:

и

вновь являясь функцией лишь крайних из оставшихся членов.
Мы видим новый по сравнению с нормальным законом распределения эффект — ценность приобрели именно крайние члены, именно они определяют эффективность оценок.
Эффективность оценки  не зависит от того, с какого края и какое количество наблюдений усечено. Эффективность наибольшая, когда при одинаковом общем числе отсутствующих наблюдений с обоих краев усечено их поровну. Для оценки размаха вообще важно знать лишь общий объем отброшенных наблюдений.
не зависит от того, с какого края и какое количество наблюдений усечено. Эффективность наибольшая, когда при одинаковом общем числе отсутствующих наблюдений с обоих краев усечено их поровну. Для оценки размаха вообще важно знать лишь общий объем отброшенных наблюдений.
Очень чувствительны к потере крайних значений оценки начальной а и конечной  точек интервала распределения: у
точек интервала распределения: у

и

Стоит здесь утратить одно или два крайних значения, как точность оценки падает в несколько раз. Наблюдения же с противоположного края выборки не оказывают сколько-нибудь заметного влияния на точность оценки и не могут компенсировать потерю крайних, «с другого берега».
Эти свойства равномерного распределения (и целого класса других) должны предостеречь экспериментаторов от необдуманного отбрасывания крайних наблюдений. Всегда нужно иметь в виду, что правомочность этой процедуры определяется видом закона распределения наблюдаемой в эксперименте случайной величины.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
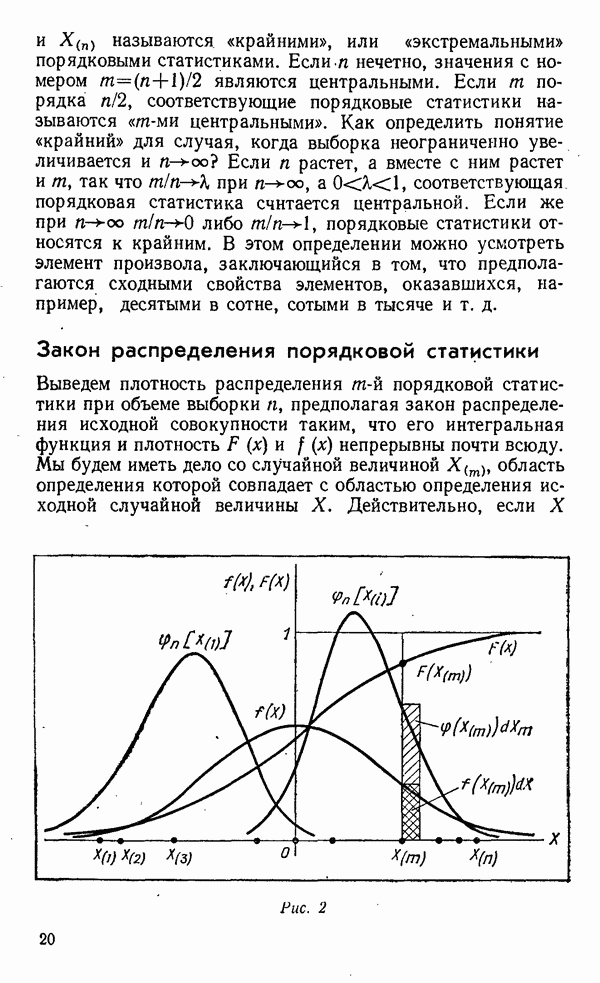
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
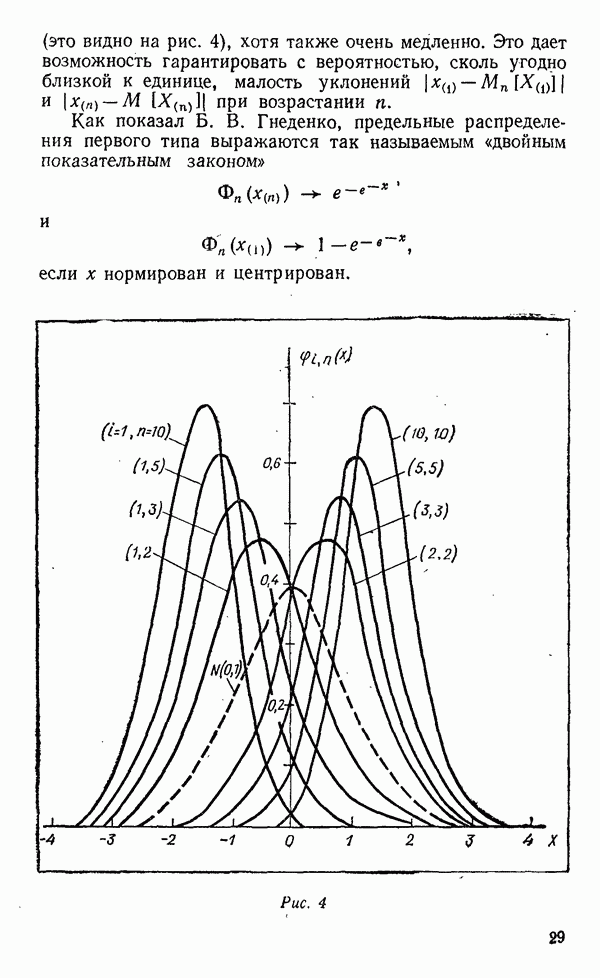
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
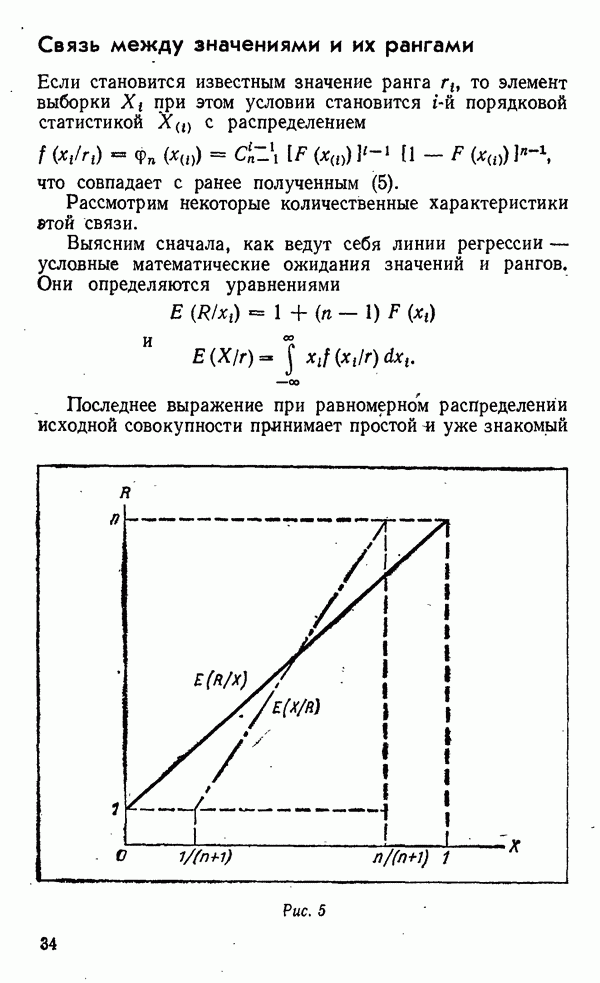
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
- Идентификация объекта с ненаблюдаемым входом
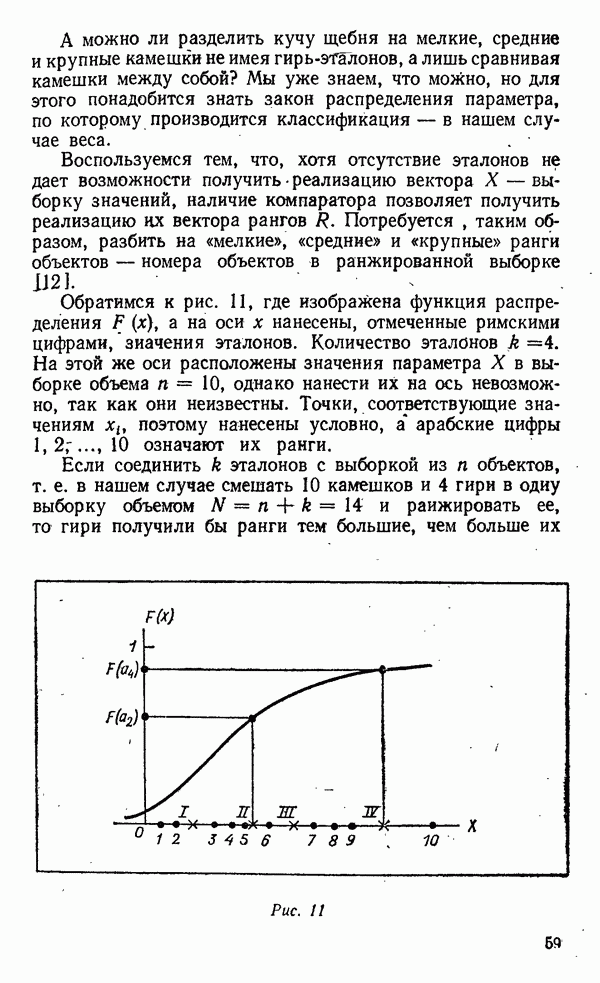
- Безэталонная классификация
- ЛИТЕРАТУРА