| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Как упорядочить выборку?
Нас в дальнейшем будут интересовать выборки, упорядоченные по значениям их элементов.
Условимся для определенности считать все элементы выборки сравнимыми между собой попарно, но несовпадающими по значениям. Это даст возможность говорить о совершенном строгом порядке. Для нумерации упорядоченных элементов будем использовать числа натурального ряда  хотя могли бы в принципе использовать любой другой его отрезок соответствующей длины.
хотя могли бы в принципе использовать любой другой его отрезок соответствующей длины.
Как мы действуем, упорядочивая последовательность чисел? Такой вопрос может поставить человека в тупик, во всяком случае, не подумав, не перечислишь операции, которые приходится проделать, превращая ряд чисел 2, 5, 1,
4, 3, 8 в ранжированную последовательность 1, 2, 3, 4, 5, 8. Да и нужно ли  перечислять? Ведь и так, неосознанно, мы. справляемся с этой задачей!
перечислять? Ведь и так, неосознанно, мы. справляемся с этой задачей!
Формализовать процедуру упорядочения, однако, необходимо, если мы хотим, чтобы эту работу выполняла  Это как раз работа для машины, особенно, если упорядочивать приходится большие массивы чисел. Познакомимся, следуя [3], с некоторыми алгоритмами упорядочивания, именуемыми еще «алгоритмами сортировки»
Это как раз работа для машины, особенно, если упорядочивать приходится большие массивы чисел. Познакомимся, следуя [3], с некоторыми алгоритмами упорядочивания, именуемыми еще «алгоритмами сортировки»
Сортировка выбором.  нужно ранжировать выборку
нужно ранжировать выборку  Выбираем наибольший элемент из
Выбираем наибольший элемент из  и меняем его местами с
и меняем его местами с  затем выбираем наибольший элемент из последовательности
затем выбираем наибольший элемент из последовательности  и меняем его местами с
и меняем его местами с  и т. д. Этот метод требует
и т. д. Этот метод требует  сравнений элементов между собой.
сравнений элементов между собой.
Сортировка попарной перестановкой. При первом просмотре каждое значение х, сравнивается с  пары элементов, для которых справедливо неравенство
пары элементов, для которых справедливо неравенство  меняются местами. Таким образом,
меняются местами. Таким образом,
наибольший элемент попадает в положение  и в последующих просмотрах уже не участвует. Количество сравнений Здесь примерно такое же, как и в первом способе, но вависит от начальных свойств выборки. Так, для выборки 3, 2, 1, 6, 4, 5 сортировка выполняется за три просмотра (при третьем просмотре перестановок нет), а сортировка выборки
и в последующих просмотрах уже не участвует. Количество сравнений Здесь примерно такое же, как и в первом способе, но вависит от начальных свойств выборки. Так, для выборки 3, 2, 1, 6, 4, 5 сортировка выполняется за три просмотра (при третьем просмотре перестановок нет), а сортировка выборки  требует 5 просмотров только ради того, чтобы один последний элемент передвинуть на первое место. Видно, что «более ранжированная» исходная выборка требует меньшего количества просмотров.
требует 5 просмотров только ради того, чтобы один последний элемент передвинуть на первое место. Видно, что «более ранжированная» исходная выборка требует меньшего количества просмотров.
Сортировка объединением именно это и использует. Элементы выборки соединяются попарно, причем меньший элемент ставится на первое место. Затем эти упорядоченные пары объединяются в четверки, четверки ранжируются и объединяются в восьмерки и т. д.
Метод наиболее эффективен, когда объем выборки равен степени двойки:  При этом необходимое количество просмотров равно
При этом необходимое количество просмотров равно  а число сравнений не превосходит
а число сравнений не превосходит 
При  попарное объединение потребует около 10000 сравнений, а сортировка попарной перестановкой потребует их в 50 раз больше.
попарное объединение потребует около 10000 сравнений, а сортировка попарной перестановкой потребует их в 50 раз больше.
Чем оплачивается такая экономия? Метод сортировки объединением требует запоминания промежуточных групп элементов — нужно  ячеек, — а метод попарной перестановки не требует промежуточного запоминания вовсе.
ячеек, — а метод попарной перестановки не требует промежуточного запоминания вовсе.
Эти же алгоритмы или их модификации используются, когда над выборкой требуется совершить какую-либо иную, связанную с упорядочиванием операцию — выбор наименьшего или наибольшего ее члена, элемента, занимающего среднее положение или имеющего определенный номер в упорядоченном ряду.
Нужно сказать, что в попытках формализовать процедуру упорядочения были перепробованы различные методы. Так, например, если смотреть на логическую операцию дизъюнкцию как на выбор максимального значения, а конъюнкции придать смысл выбора минимального значения, то при помощи логических дизъюнктивно-конъюнктивных форм можно описать и процесс ранжирования, и другие процедуры сортировки [4].
Покажем это «а примере выбора срединного значения — медианы выборки, предположив для простоты, что число членов выборки нечетио и что равных значений в выборке нет.
Итак, если объем выборки нечетен,  медианное значение в ранжированной выборке займет место с номером
медианное значение в ранжированной выборке займет место с номером  При этом оно будет больше всех предыдущих и меньше последующих, количество которых одинаково
При этом оно будет больше всех предыдущих и меньше последующих, количество которых одинаково  , и может быть найдено, как
, и может быть найдено, как

Здесь  наибольшие из всевозможных сочетаний элементов по
наибольшие из всевозможных сочетаний элементов по 
Величины  определяются как наименьшие из сочетаний по
определяются как наименьшие из сочетаний по 
Количество  одинаково:
одинаково: 
Пусть  Процедура выделения медианы будет выглядеть так:
Процедура выделения медианы будет выглядеть так:

Или так:

В рассмотренных алгоритмах сортировки мы оперировали с выборками значений  заданных в виде чисел, и имели в качестве элементарной операции операцию сравнения двух элементов выборки
заданных в виде чисел, и имели в качестве элементарной операции операцию сравнения двух элементов выборки  (двух чисел). Сравнение может быть осуществлено путем вычитания
(двух чисел). Сравнение может быть осуществлено путем вычитания  Положительный знак разности влечет вывод
Положительный знак разности влечет вывод  больше, чем
больше, чем  отрицательный приводит к противоположному заключению.
отрицательный приводит к противоположному заключению.
А как производить ранжирование выборки, состоящей не из чиаел, а из объектов  принадлежащих множеству К?
принадлежащих множеству К?
Очевидный путь — измерить  и, определив значения
и, определив значения  оперировать ими, как было показано выше. К сожалению, очевидными путями не всегда удается воспользоваться. Как быть, если измерять объекты и, нельзя? Веда может оказаться, что интересующий нас параметр этих объектов неизмерим в принципе, как неизмерима, например, «сила игры» шахматиста (шахматной программы) или доблесть рыцаря.
оперировать ими, как было показано выше. К сожалению, очевидными путями не всегда удается воспользоваться. Как быть, если измерять объекты и, нельзя? Веда может оказаться, что интересующий нас параметр этих объектов неизмерим в принципе, как неизмерима, например, «сила игры» шахматиста (шахматной программы) или доблесть рыцаря.
Возможен и другой случай, когда параметр объекта нечем измерить из-за отсутствия измерительного прибора.
Так обстоит дело, например, с определением интенсивности аапаха.
Однако мы видели, что алгоритмы сортировки используют значения  для вынесения суждений «больше — меньше» в процессе парных сравнений, а парные сравнения зачастую могут быть произведены и между элементами выборки
для вынесения суждений «больше — меньше» в процессе парных сравнений, а парные сравнения зачастую могут быть произведены и между элементами выборки  непосредственно, без определения их значений.
непосредственно, без определения их значений.
Действительно, если речь идет о «силе игры» — параметре неизмеримом, то процедура типа турнира, основанная на парных взаимодействиях участников, дает материал именно для ранжирования их по значениям неизмеримого параметра.
Другой способ упорядочения — экспертные оценки — особенно эффективен при вынесении решений о парных соотношениях.
Наконец, для непосредственного сравнения объектов могут быть использованы специальные устройства сравнения — компараторы. Так, при ранжировании по весу компараторами могут быть рычажные весы без гирь. Электрические сигналы могут сравниваться между собой, например, на мостовых схемах и т. д.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
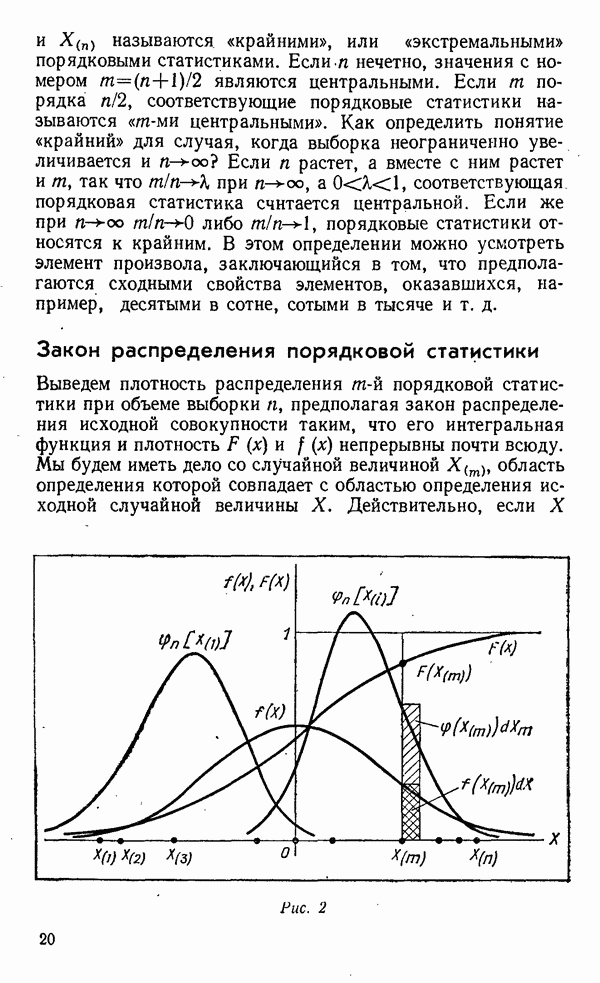
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
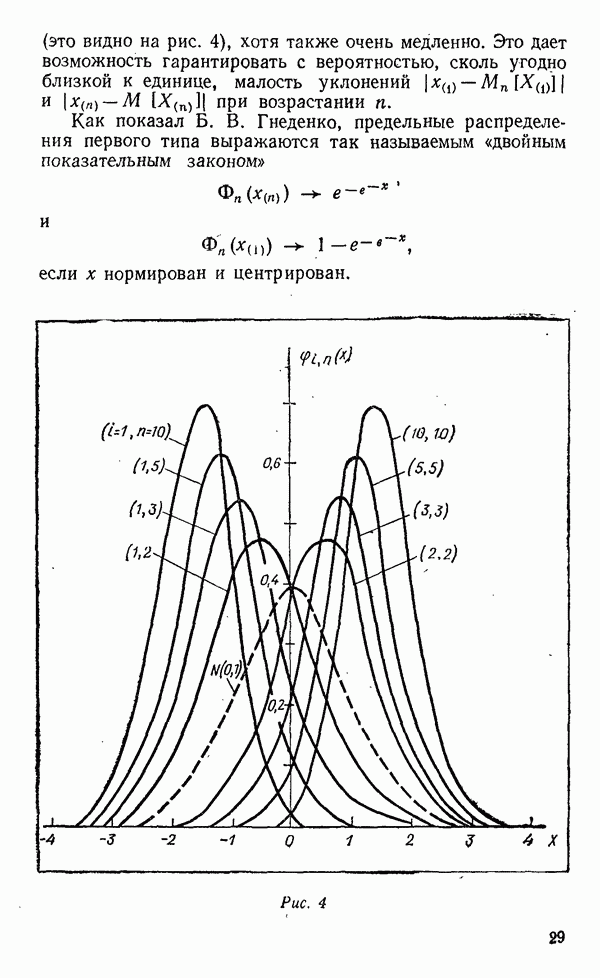
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
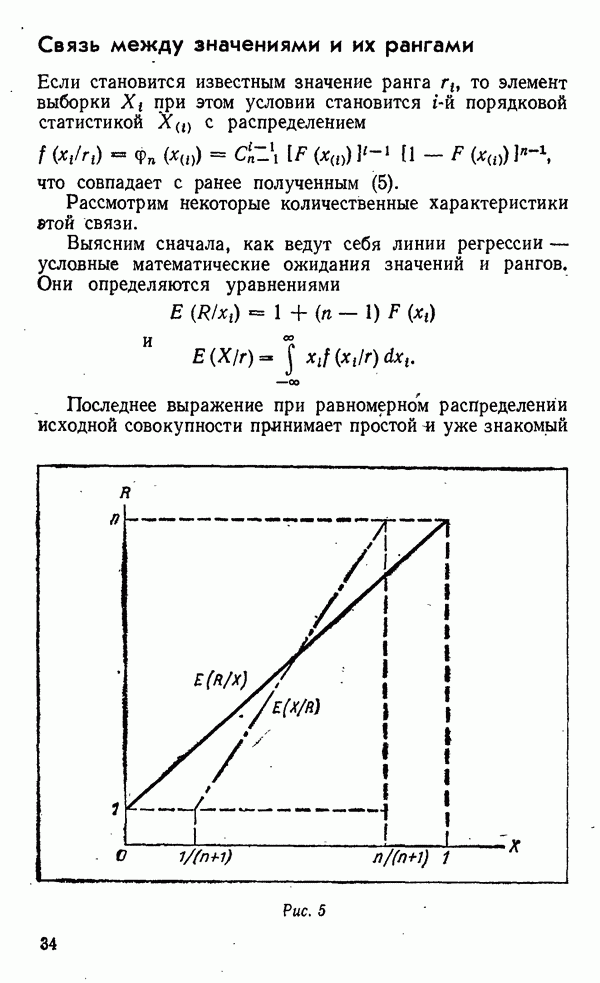
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
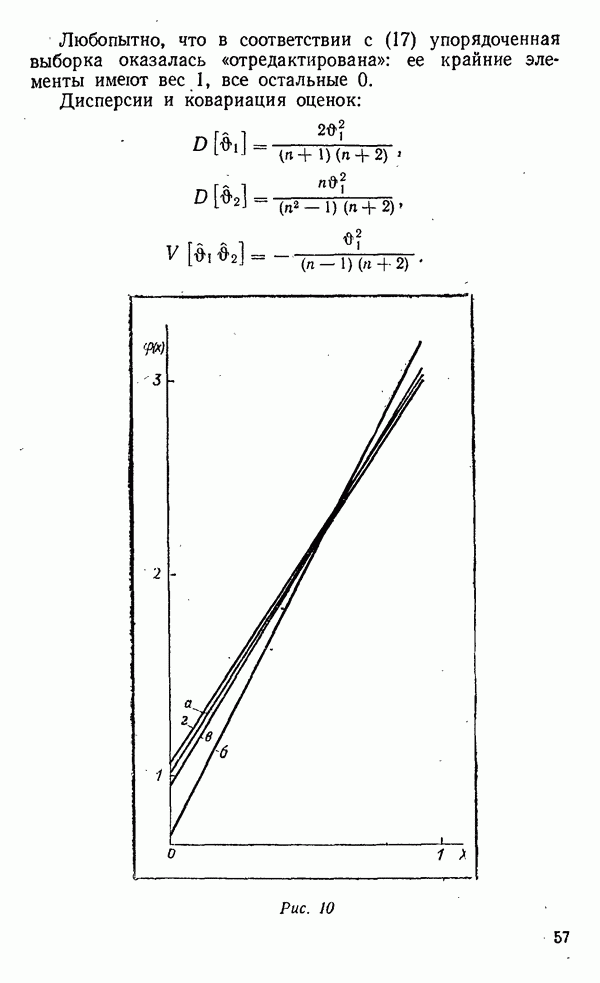
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
- Идентификация объекта с ненаблюдаемым входом
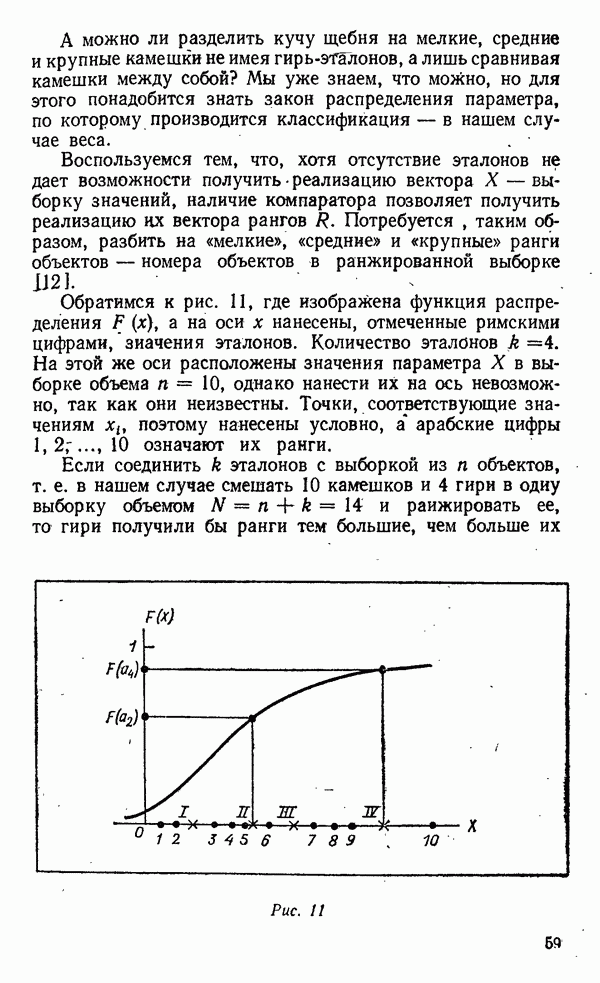
- Безэталонная классификация
- ЛИТЕРАТУРА