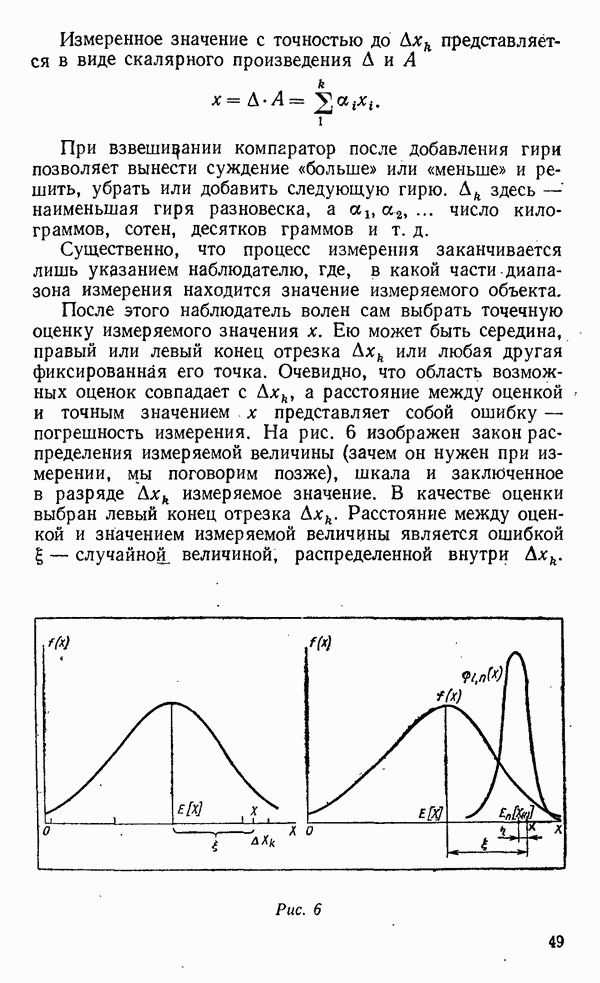
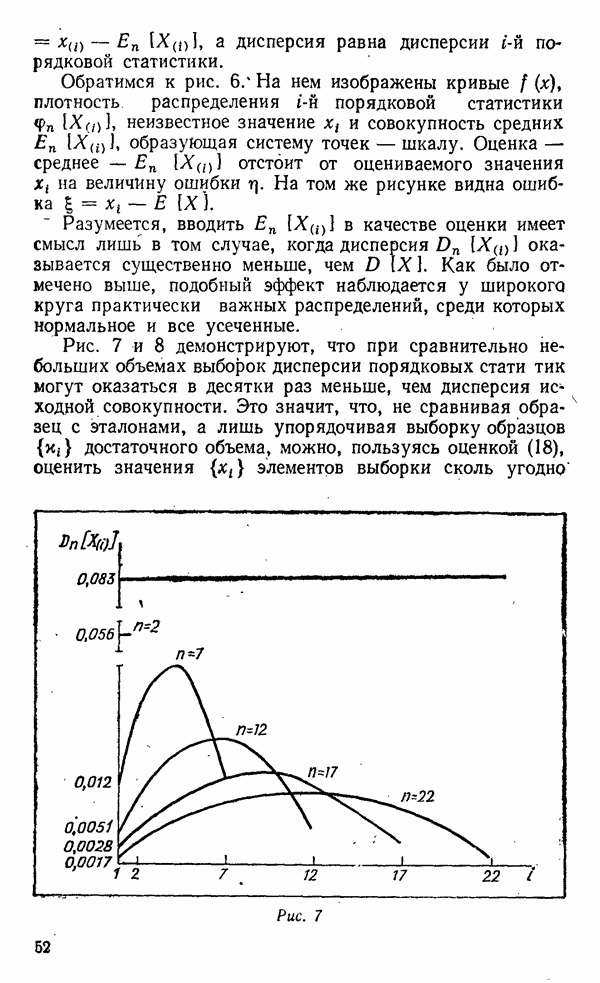
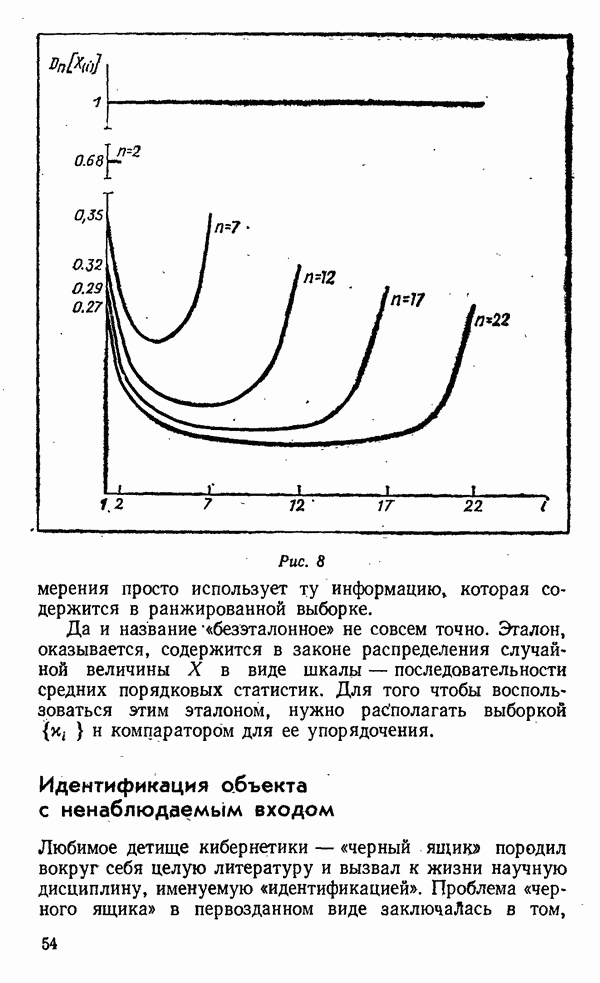
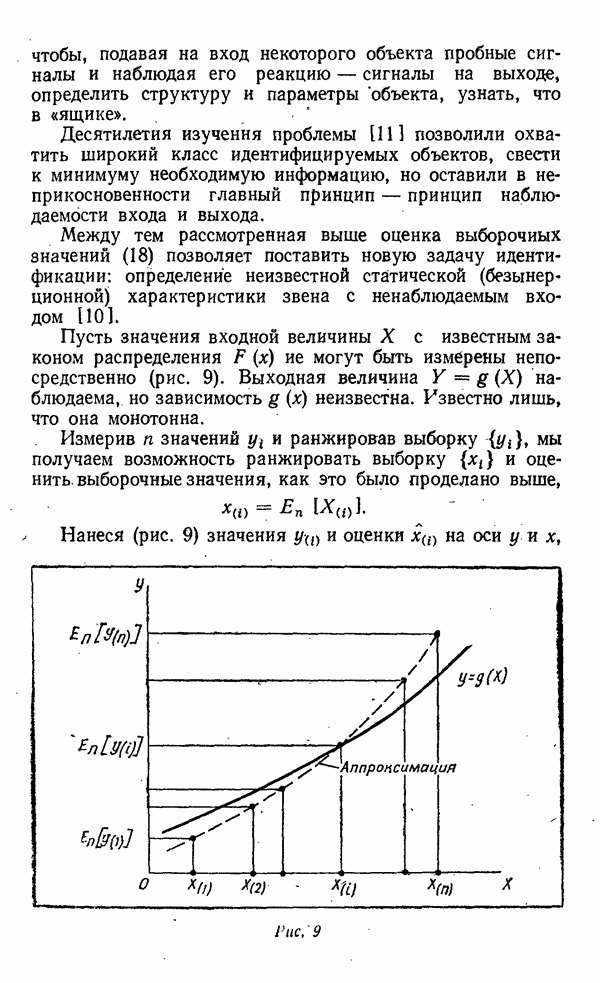
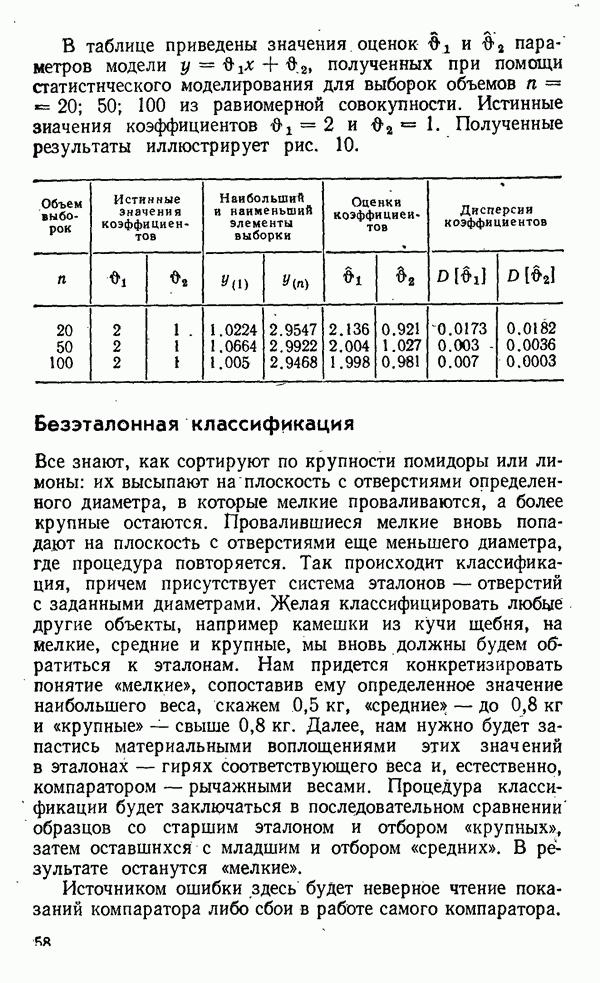
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Безэталонная классификация
Все знают, как сортируют по крупности помидоры или лимоны: их высыпают на плоскость с отверстиями определенного диаметра, в которые мелкие проваливаются, а более крупные остаются. Провалившиеся мелкие вновь попадают на плоскость с отверстиями еще меньшего диаметра, где процедура повторяется. Так происходит классификация, причем присутствует система эталонов — отверстий с заданными диаметрами. Желая классифицировать любые другие объекты, например камешки из кучи щебня, на мелкие, средние и крупные, мы вновь должны будем обратиться к эталонам. Нам придется конкретизировать понятие «мелкие», сопоставив ему определенное значение наибольшего веса, скажем  «средние» — до
«средние» — до  и «крупные» — свыше
и «крупные» — свыше  Далее, нам нужно будет запастись материальными воплощениями этих значений в эталонах — гирях соответствующего веса и, естественно, компаратором — рычажными весами. Процедура классификации будет заключаться в последовательном сравнении образцов со старшим эталоном и отбором «крупных», затем оставшихся с младшим и отбором «средних». В результате останутся «мелкие».
Далее, нам нужно будет запастись материальными воплощениями этих значений в эталонах — гирях соответствующего веса и, естественно, компаратором — рычажными весами. Процедура классификации будет заключаться в последовательном сравнении образцов со старшим эталоном и отбором «крупных», затем оставшихся с младшим и отбором «средних». В результате останутся «мелкие».
Источником ошибки здесь будет неверное чтение показаний компаратора либо сбои в работе самого компаратора.
А можно ли разделить кучу щебня на мелкие, средние и крупные камешки не имея гирь-эталонов, а лишь сравнивая камешки между собой? Мы уже знаем, что можно, но для этого понадобится знать закон распределения параметра, по которому производится классификация — в нашем случае веса.
Воспользуемся тем, что, хотя отсутствие эталонов не дает возможности получить реализацию вектора X — выборку значений, наличие компаратора позволяет получить реализацию  вектора рангов
вектора рангов  Потребуется таким образом, разбить на «мелкие», «средние» и «крупные» ранги объектов — номера объектов в ранжированной выборке
Потребуется таким образом, разбить на «мелкие», «средние» и «крупные» ранги объектов — номера объектов в ранжированной выборке 
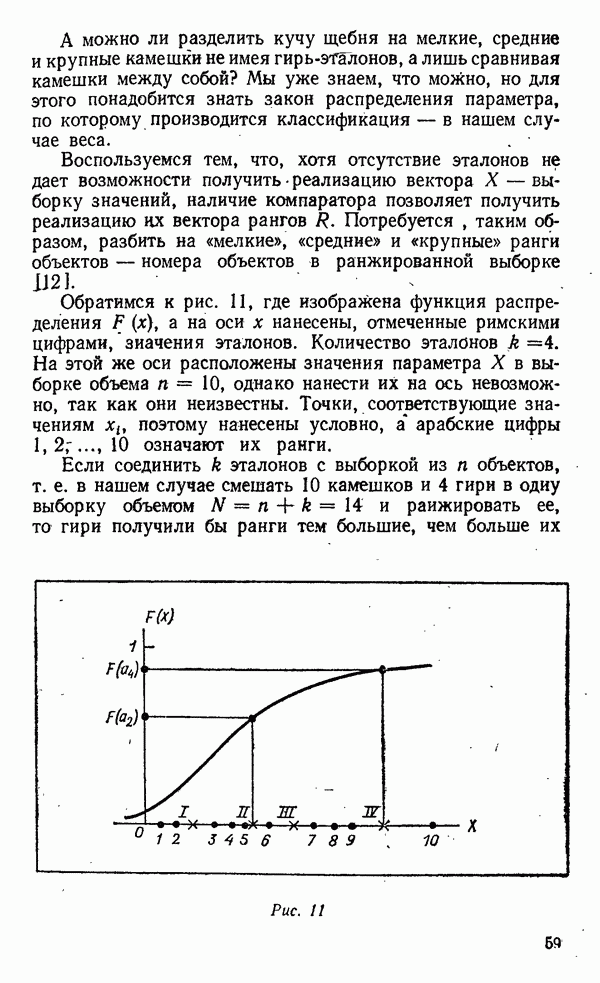
Обратимся к рис. 11, где изображена функция распределения  а на оси х нанесены, отмеченные римскими цифрами, значения эталонов. Количество эталонов
а на оси х нанесены, отмеченные римскими цифрами, значения эталонов. Количество эталонов  На этой же оси расположены значения параметра X в выборке объема
На этой же оси расположены значения параметра X в выборке объема  однако нанести их на ось невозможно, так как они неизвестны. Точки, соответствующие значениям
однако нанести их на ось невозможно, так как они неизвестны. Точки, соответствующие значениям  поэтому нанесены условно, а арабские цифры
поэтому нанесены условно, а арабские цифры  означают их ранги.
означают их ранги.
Если соединить  эталонов с выборкой из
эталонов с выборкой из  объектов, т. е. в нашем случае смешать 10 камешков и 4 гири в одну выборку объемом
объектов, т. е. в нашем случае смешать 10 камешков и 4 гири в одну выборку объемом  и ранжировать ее, то гири получили бы ранги тем большие, чем больше их
и ранжировать ее, то гири получили бы ранги тем большие, чем больше их

Рис. II
вес. Если с этими же гирями смешивать все новые и новые десятки камешков, можно заметить, что ранги гирь варьируют от выборки к выборке тем меньше, чем больше 
Теперь принцип классификации без эталона ясен: нужно, зная  и
и  определить ранги эталонов
определить ранги эталонов  в выборке объемом
в выборке объемом  а затем разбить пространство рангов на
а затем разбить пространство рангов на  область, сравнивая ранги объектов с рангами эталонов. При этом произойдет и классификация объектов по значениям параметра X (по-прежнему неизвестным нам), поскольку, как было показано выше, ранги и соответствующие им выборочные значения связаны тем более тесно, чем больше объем выборки.
область, сравнивая ранги объектов с рангами эталонов. При этом произойдет и классификация объектов по значениям параметра X (по-прежнему неизвестным нам), поскольку, как было показано выше, ранги и соответствующие им выборочные значения связаны тем более тесно, чем больше объем выборки.
Источником ошибок классификации является конечность выборки, не позволяющая точно определять ранги значений эталонов. Задавшись, однако, значениями ошибок первого и второго рода, можно определить необходимый для получения требуемой точности объем выборки.
Итак, закон распределения случайной величины заключает в себе шкалу (эталон), а компаратор, воплощенный в той или иной форме, позволяет эту шкалу построить и использовать для оценивания, идентификации и классификации.
Все это очень интересно, скажет искушенный читатель, но где же взять закон распределения параметра, который неизмерим? Ведь закон распределения строится именно путем обработки большого числа измерений случайной величины. В силу такой точки зрения закон распределения неизмеримого параметра считается неизвестным, а вернее, просто не вызывает интереса у исследователей. Принято считать, что если измерение возможно, он не нужен, а если невозможно — бесполезен. Однако физики знают множество примеров, когда распределение величины известно из теории, а измерение ее выборочного значения невозможно или затруднительно. Так, скорость молекул газа в сосуде подчинена закону распределения Максвелла с известными параметрами, если известны давление и температура.
Точно также без наблюдения за отдельными молекулами можно указать закон распределения их удаления от какой-либо исходной точки при диффузии. Кроме того, существуют величины, неизмеримость которых относительна. Сейчас мы фиксируем скорость бегуна секундомером, а у древних греков не было эталона подходящего масштаба для измерения времени бега на спортивных соревнованиях,
поэтому на олимпиадах древности могла быть зафиксирована лишь последовательность - бегунов на финише — их ранги. Тем не менее каждый бегун обладал определенным значением неизмеримого тогда параметра — скорости. Сейчас эта «величина в себе» объективизировалась так, что известны и ее закон распределения, и мгновенные значения.
Таким образом, безэталониые процедуры могут, с одной стороны, найти область приложения, где законы распределения уже известны, а с другой — стимулировать процесс выяснения этих законов.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
- Идентификация объекта с ненаблюдаемым входом
- Безэталонная классификация
- ЛИТЕРАТУРА