| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
Говоря о представительности выборки, мы обсуждали способы страховки от ошибок путем организации такой процедуры отбора, которая достаточно полно отразила бы в небольшой по объему выборке всю (в принципе бесконечную) генеральную совокупность.
Но вот выборка сформирована, и на ее основе будет сделан статистический вывод, например оценен какой-то параметр распределения генеральной совокупности. Точность при этом будет зависеть, при заданном объеме выборки, от свойств оценки и вида закона распределения. Но быть уверенным в том, что подсчитанная в такой ситуации точность оценки отвечает действительности, можно лишь в том случае, если высока надежность оценки и если мы полностью уверены в представительности и независимости выборки. Действительно, применение мощного математического аппарата, сулящего высокую точность оценок, к ненадежным данным не только бессмысленно, но и опасно, так как порождает необоснованные надежды «замолить грехи» эксперимента. С другой стороны, нерационально результаты надежного эксперимента обрабатывать «на глазок», с низкой точностью. Очевидно, между надежностью данных и точностью обработки существует некоторое оптимальное соотношение. К сожалению, даже относительно выборок, сформированных «по всем правилам», обычно остаются сомнения, причем касаются они, как правило, тех ее членов, которые занимают в вариационном ряду значений крайние места.
Сомнения эти порождаются двумя основными причинами.
Во-первых, нередки - случаи, когда генеральная совокупность, из которой формируется выборка, в принципе неоднородна — представляет собой смесь двух или нескольких совокупностей, отличающихся, например, средними значениями. Ясно, что попадание в выборку нескольких «сорных» значений способно лишь исказить оценку среднего. Поэтому, если бы удалось «узнать» эти «сорные» значения и отбросить их, качество оценки могло бы возрасти. Разумеется, если вместо «Сорных» отбросить «правильные» элементы выборки, перепутав их, точность понизится еще и за счет укорочения выборки.
Во-вторых, измерительные приборы имеют, как правило, наилучшие точностные характеристики в середине
шкалы. Наибольшие и наименьшие результаты измерений могут быть искажены нелинейностью градуировочной характеристики и действием помех, почему и вызывают подозрения относительно их надежности.
В упоминавшейся книге М. Кендалла и А. Стьюарта приводится очень удачный пример эксперимента, в котором происходит отбрасывание крайних (цензурирование выборки).
Пусть производится стрельба по круглой мишени радиуса  и регистрируется расстояние между точками попадания и центром мишени. При
и регистрируется расстояние между точками попадания и центром мишени. При  выстрелах и
выстрелах и  попаданиях разность
попаданиях разность  составляет количество отброшенных (справа!) наблюдений, а уровень
составляет количество отброшенных (справа!) наблюдений, а уровень  является уровнем урезания распределения
является уровнем урезания распределения  В экспериментальной практике исследователи, вначале руководствуясь интуицией, издавна стали просто отбрасывать крайние наблюдения. Этот способ позднее подвергся строгому анализу и получил название «цензурирование выборок». Анализ, как это обычно и бывает при анализе интуитивных предположений, дал количественные оценки эффективности метода и указал границы его применимости. Мы покажем, что результаты анализа, а это бывает редко, продвинулись дальше и смелее интуитивных выводов: оказалось, например, что в некоторых случаях нужно отбрасывать не крайние, а средние наблюдения!
В экспериментальной практике исследователи, вначале руководствуясь интуицией, издавна стали просто отбрасывать крайние наблюдения. Этот способ позднее подвергся строгому анализу и получил название «цензурирование выборок». Анализ, как это обычно и бывает при анализе интуитивных предположений, дал количественные оценки эффективности метода и указал границы его применимости. Мы покажем, что результаты анализа, а это бывает редко, продвинулись дальше и смелее интуитивных выводов: оказалось, например, что в некоторых случаях нужно отбрасывать не крайние, а средние наблюдения!
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
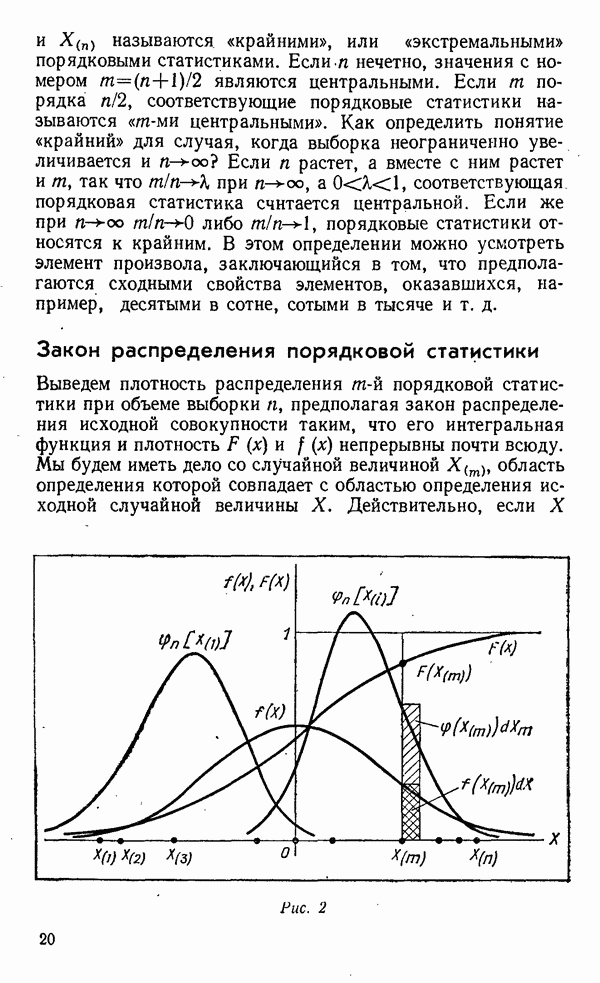
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
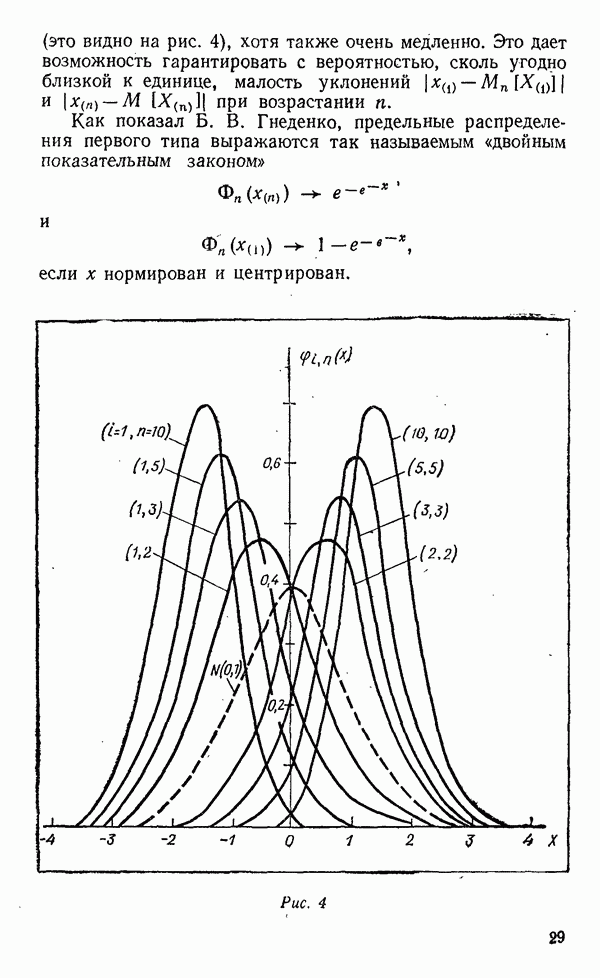
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
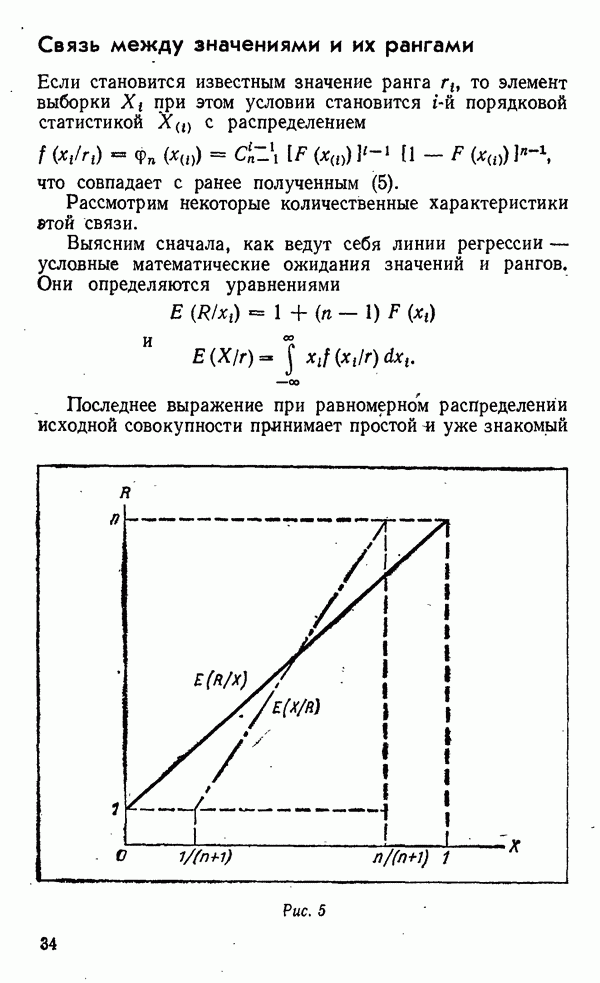
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
- Идентификация объекта с ненаблюдаемым входом
- Безэталонная классификация
- ЛИТЕРАТУРА