| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
В предыдущих разделах было показано, как методы порядковых статистик работают «внутри» статистики, помогая
решать задачи оценивания, проверки гипотез, редактирования наблюдений.
Здесь мы продемонстрируем, как с их помощью могут быть решены некоторые прикладные задачи.
Измерение без эталона
Если мы хотим произвести измерение некоторого параметра, то должны располагать, во-первых, материальным носителем этого параметра — объектом измерения, во-вторых, эталоном — носителем единицы, в которой должен выразиться результат измерения, и, в-третьих, компаратором — устройством, при помощи которого объект измерения будет сравниваться с эталоном.
Так, если измеряемый параметр X — это вес (точнее, масса) тела, то объект измерения должен быть тяготеющей массой. Говорить о весе меридиана, улыбки или квадратного трехчлена бессмысленно. При взвешивании эталоном выступает образцовая мера веса, воплощенная в наборе гирь — разновесок. Значения разновесок образуют шкалу — систему эталонных мер. Компаратором являются привычные нам рычажные весы.
Объект X может быть случайной величиной либо процессом, принимать дискретные либо непрерывные значения.
Систему эталонов представим в виде вектора эталонных мер

где величина  эталона в простейшем случае определяется, как
эталона в простейшем случае определяется, как

Здесь  то, что принято именовать «ценой разряда»;
то, что принято именовать «ценой разряда»;
 основание принятой системы счисления, в которой формируется результат, обычно
основание принятой системы счисления, в которой формируется результат, обычно  либо 2;
либо 2;
 количество разрядов результата измерения;
количество разрядов результата измерения;
 младший разряд результата, имеющий смысл разрешающей способности.
младший разряд результата, имеющий смысл разрешающей способности.
Измерительная процедура заключается в том, что значение измеряемой величины последовательно локализуют в сужающихся областях  образуя результат измерения — число
образуя результат измерения — число 
Измеренное значение с точностью до  представляется в виде скалярного произведения
представляется в виде скалярного произведения 

При взвешивании компгратор после добавления гири позволяет вынести суждение «больше» или «меньше» и решить, убрать или добавить следующую гирю.  здесь — наименьшая гиря разновеска, а
здесь — наименьшая гиря разновеска, а  число килограммов, сотен, десятков граммов и т. д.
число килограммов, сотен, десятков граммов и т. д.
Существенно, что процесс измерения заканчивается лишь указанием наблюдателю, где, в какой части диапазона измерения находится значение измеряемого объекта.
После этого наблюдатель волен сам выбрать точечную оценку измеряемого значения х. Ею может быть середина, правый или левый конец отрезка  или любая другая фиксированная его точка. Очевидно, что область возможных оценок совпадает с
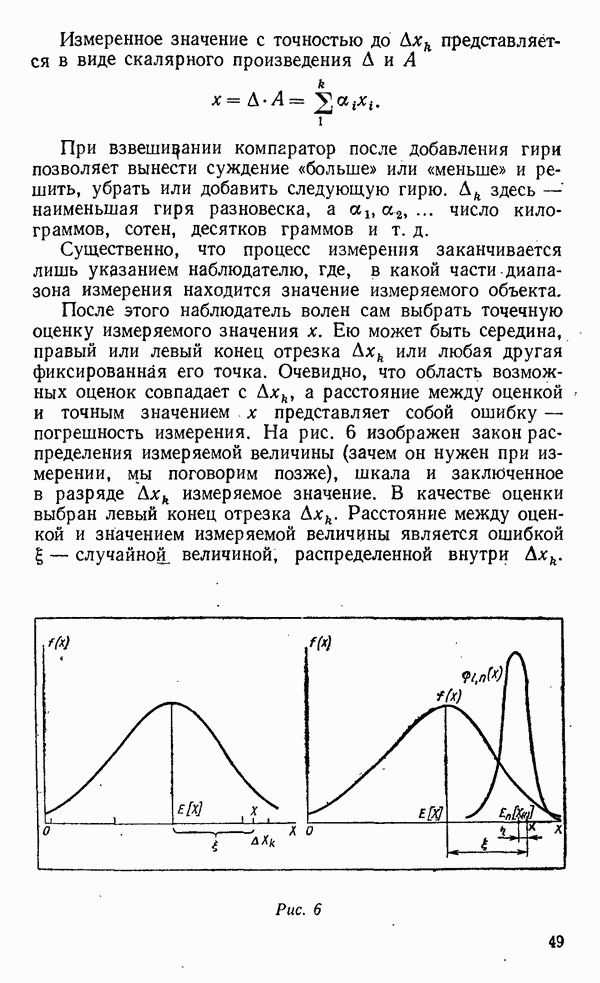
или любая другая фиксированная его точка. Очевидно, что область возможных оценок совпадает с  а расстояние между оценкой и точным значением х представляет собой ошибку — погрешность измерения. На рис. 6 изображен закон распределения измеряемой величины (зачем он нужен при измерении, мы поговорим позже), шкала и заключенное в разряде
а расстояние между оценкой и точным значением х представляет собой ошибку — погрешность измерения. На рис. 6 изображен закон распределения измеряемой величины (зачем он нужен при измерении, мы поговорим позже), шкала и заключенное в разряде  измеряемое значение. В качестве оценки выбран левый конец отрезка
измеряемое значение. В качестве оценки выбран левый конец отрезка  Расстояние между оценкой и значением измеряемой величины является ошибкой
Расстояние между оценкой и значением измеряемой величины является ошибкой  случайной, величиной, распределенной внутри
случайной, величиной, распределенной внутри 

Рис. 6
Как мы видели, закон распределения не учитывался в процессе измерения. Если он известен, то в принципе можно построить оптимальную шкалу и получить ту же разрешающую способность за меньшее число сравнений.
Описанная измерительная процедура является основой для экспериментальной базы точных и естественных наук.
К сожалению, осуществить измерения возможно далеко не всегда. Можно указать две принципиальные причины, по которым измерение не может быть выполнено: отсутствие эталона и невозможность сравнения измеряемой величины с эталоном, пусть даже существующим.
Попытки преодолеть эти трудности привели к различным методам оценивания, называемым «неметрическим шкалированием». Термин «шкалирование» означает получение количественной информации об объекте в тех случаях, когда объективное измерение невозможно.
Ряд научных дисциплин обрел экспериментальную базу, разработав методы интервального неметрического шкалирования, создав, таким образом, суррогат измерения.
Шкалирование или ранжирование при помощи экспертных оценок представляет собой попытку справиться с трудностью второго рода. Подразумевается, что эксперт при этом выступает в роли носителя эталона (шкалы), с которым эвристически соотносит оцениваемую величину. Проводя аналогию между экспертом и измерительным прибором, можно, очевидно, говорить о «разрешающей способности» эксперта. Этот термин характеризует «систему эталонов» — «шкалу», которой вооружены органы чувств или интуиция эксперта, позволяющая ему проводить более или менее тонкие градаций предъявляемых значений величины — от суждений «больше — меньше» до присвоения числовых значений.
Сложнее оценить количественно явления, для которых не существует эталона, даже неформального. Как, например, количественно оценить уже упоминавшиеся «Доблесть рыцаря», «силу игры» футбольной команды или «эвристическую силу» интеллектуальной (шахматной, например) программы?
Если эталона для измерения подобного свойства в принципе не существует, ранжирование объектов по значениям этой величины может в ряде случаев быть осуществлено путем организации специальной процедуры взаимодействия между объектами — процедуры типа игры, поединка, конфликта. При этом подразумевается, что
каждому из соперников присуще значение некоторого параметра — «силы игры» («доблести»), принципиально неизмеримого (иначе не нужбн был бы турнир !), но объективно существующего и подчиненного некоторому закону распределения.
Теория измерений довольно скупо вознаграждает наблюдателя, снабженного прибором, за знание им закона распределения: с его помощью можно лишь несколько улучшить измерительную процедуру, повысив (на практике не намного) разрешающую способность.
Если же прибора нет, а закон  известен, лучшее, что может предпринять наблюдатель, выбрать в качестве оценки любого значения среднее
известен, лучшее, что может предпринять наблюдатель, выбрать в качестве оценки любого значения среднее  что, конечно, представляет собой очень грубую оценку: дисперсия ошибки
что, конечно, представляет собой очень грубую оценку: дисперсия ошибки  равна при этом дисперсии величины X и улучшена быть не может.
равна при этом дисперсии величины X и улучшена быть не может.
Здесь мы продемонстрируем, как, пользуясь свойствами порядковых статистик, можно получить количественные оценки (иногда в принципе сколь угодно точные) величин, для измерения которых не существует эталона, но известен закон распределения и допустимо ранжирование. Применительно к нашему примеру со щебнем это означает, что мы, зная  будем пытаться взвесить отдельные камешки на весах, не имея... гирь!
будем пытаться взвесить отдельные камешки на весах, не имея... гирь!
Обратимся к идее безэталонного измерения  Пусть К-генеральная совокупность образцов к; X — генеральная совокупность присущих им значений х, подчиненная закону
Пусть К-генеральная совокупность образцов к; X — генеральная совокупность присущих им значений х, подчиненная закону 
Образуем выборку из  -образцов
-образцов  и ранжируем ее по параметру X, используя компаратор
и ранжируем ее по параметру X, используя компаратор  Теперь и значения
Теперь и значения  соответствующие образцам образуют вариационный ряд
соответствующие образцам образуют вариационный ряд  Обратим внимание на то, что значения членов этого ряда остаются неизвестными для наблюдателя, причем он хочет оценить их. Элементы ряда
Обратим внимание на то, что значения членов этого ряда остаются неизвестными для наблюдателя, причем он хочет оценить их. Элементы ряда  представляют собой значения порядковых статистик
представляют собой значения порядковых статистик 
В качестве точечной оценки  неизвестного значения, занимающего
неизвестного значения, занимающего  место в вариационном ряду, естественно принять математическое ожидание соответствующей порядковой статистики
место в вариационном ряду, естественно принять математическое ожидание соответствующей порядковой статистики

При этом допускается ошибка, значение которой 
 а дисперсия равна дисперсии
а дисперсия равна дисперсии  порядковой статистики.
порядковой статистики.
Обратимся к рис. 6. На нем изображены кривые  плотность распределения
плотность распределения  порядковой статистики
порядковой статистики  неизвестное значение
неизвестное значение  и совокупность средних
и совокупность средних  образующая систему точек — шкалу. Оценка — среднее —
образующая систему точек — шкалу. Оценка — среднее —  отстоит от оцениваемого значения
отстоит от оцениваемого значения  на величину ошибки
на величину ошибки  На том же рисунке видна ошибка
На том же рисунке видна ошибка 
Разумеется, вводить  в качестве оценки имеет смысл лишь в том случае, когда дисперсия
в качестве оценки имеет смысл лишь в том случае, когда дисперсия  оказывается существенно меньше, чем
оказывается существенно меньше, чем  Как было отмечено выше, подобный эффект наблюдается у широкого круга практически важных распределений, среди которых нормальное и все усеченные.
Как было отмечено выше, подобный эффект наблюдается у широкого круга практически важных распределений, среди которых нормальное и все усеченные.
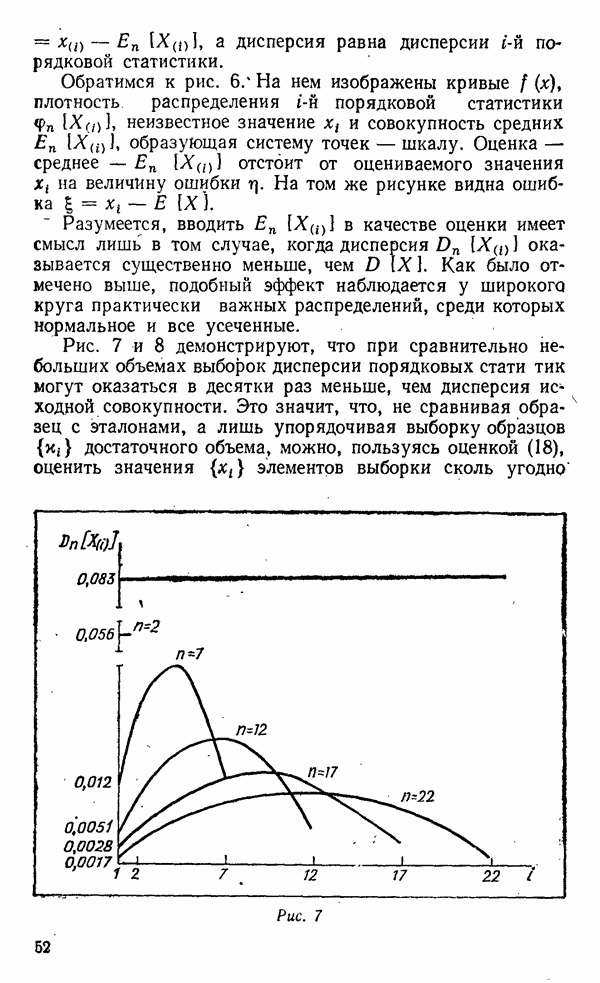
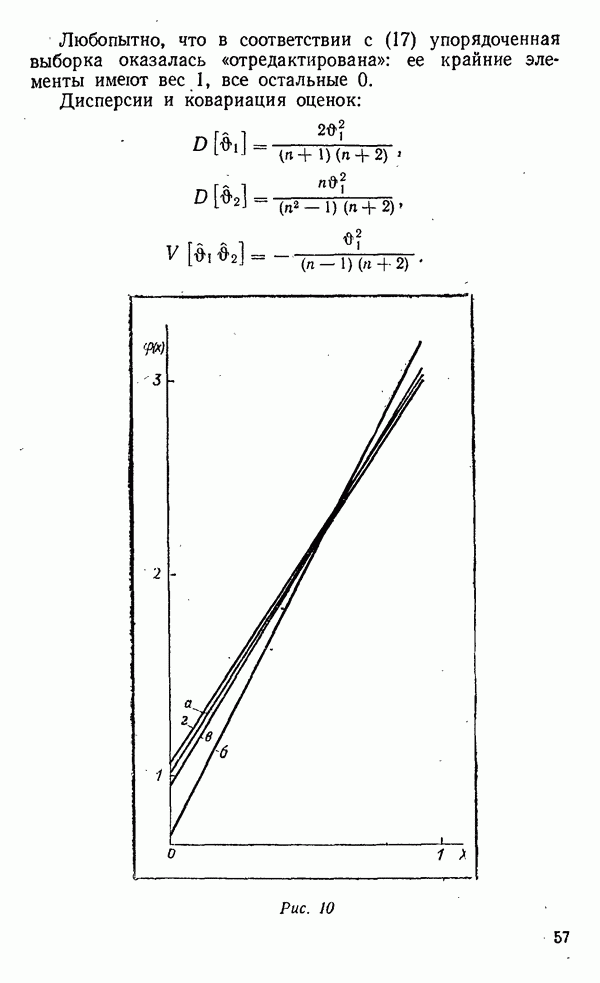
Рис. 7 и 8 демонстрируют, что при сравнительно небольших объемах выборок дисперсии порядковых стати тик могут оказаться в десятки раз меньше, чем дисперсия исходной совокупности. Это значит, что, не сравнивая образец с эталонами, а лишь упорядочивая выборку образцов  достаточного объема, можно, пользуясь оценкой (18), оценить значения
достаточного объема, можно, пользуясь оценкой (18), оценить значения  элементов выборки сколь угодно
элементов выборки сколь угодно

Рис. 7
точно в смысле дисперсии ошибки. Роль системы эталонов, роль шкалы при этом играет множество средних  При ограниченном диапазоне распределения измеряемой величины и неограниченном росте объема выборки
При ограниченном диапазоне распределения измеряемой величины и неограниченном росте объема выборки  расстояние между точками этой «шкалы» (ее «разрешающая способность») неограниченно уменьшается. Точность при таком способе измерений будет ограничиваться чувствительностью компаратора.
расстояние между точками этой «шкалы» (ее «разрешающая способность») неограниченно уменьшается. Точность при таком способе измерений будет ограничиваться чувствительностью компаратора.
Рассмотрим пример. Пусть величина X распределена равномерно в промежутке  Требуется оценить значения элементов выборки объемом
Требуется оценить значения элементов выборки объемом  Среднее
Среднее  а оценка любого выборочного значения средним
а оценка любого выборочного значения средним  приводит к ошибке с дисперсией
приводит к ошибке с дисперсией 
Ранжируем 7 элементов  и, зная закон распределения X, вычислим средние порядковых статистик и, нанося их значения на ось х, образуем шкалу. В нашем случае
и, зная закон распределения X, вычислим средние порядковых статистик и, нанося их значения на ось х, образуем шкалу. В нашем случае

Применяя оценку  приписываем наименьшему из выборки
приписываем наименьшему из выборки  значение
значение  , следующему —
, следующему —  и т. д. до
и т. д. до  Дисперсия ошибки оценивания будет различной для разных членов ранжированной выборки. Для крайних
Дисперсия ошибки оценивания будет различной для разных членов ранжированной выборки. Для крайних  для центрального —
для центрального —  Желая увеличить точность оценивания, следует увеличить выборку
Желая увеличить точность оценивания, следует увеличить выборку 
Как мы видели, ранжирование образцов позволило существенно улучшить точность оценивания присущих им значений, не пользуясь эталоном. Откуда взялась эта дополнительная информация? Не «вечный  двигатель» перед ндми? Вспомним, что ранжируя выборку, упорядочивая ее, мы понижали ее энтропию, «закачивали» в нее информацию. Каждый акт парного сравнения порождал
двигатель» перед ндми? Вспомним, что ранжируя выборку, упорядочивая ее, мы понижали ее энтропию, «закачивали» в нее информацию. Каждый акт парного сравнения порождал
1 бит информации.
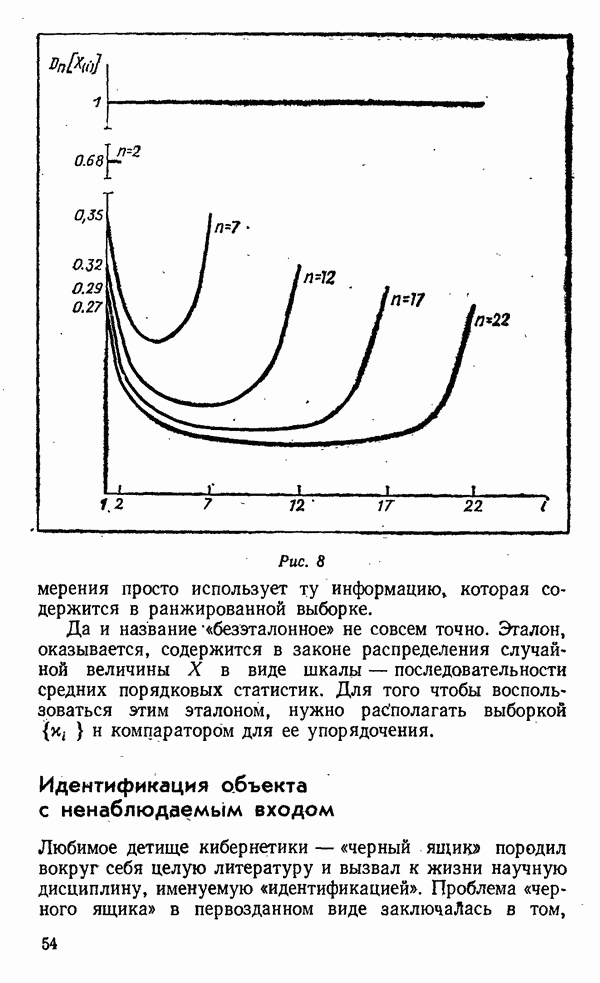
Понижение энтропии упорядоченной выборки по сравнению с неупорядоченной проявилось в том, что ее элементы оказались коррелированными — это было установлено в разделе 2. Далее выяснилось, что ранги — номера элементов в упорядоченной выборке — несут информацию о значениях, причем и степень коррелированности элементов выборки, и количество информации о значениях, заключенной в рангах, увеличивалось с ростом  Таким образом, описанная здесь процедура «безэталонного»
Таким образом, описанная здесь процедура «безэталонного»

Рис. 8
измерения просто использует ту информацию, которая содержится в ранжированной выборке.
Да и название чбезэталонное» не совсем точно. Эталон, оказывается, содержится в законе распределения случайной величины X в виде шкалы — последовательности средних порядковых статистик. Для того чтобы воспользоваться этим эталоном, нужно располагать выборкой  и компаратором для ее упорядочения.
и компаратором для ее упорядочения.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- 1. ОБРАЗОВАНИЕ И УПОРЯДОЧЕНИЕ ВЫБОРКИ
- Как упорядочить выборку?
- Ранжированная выборка — объект с новыми свойствами
- 2. ВЕРОЯТНОСТНЫЕ СВОЙСТВА ПОРЯДКОВОЙ СТАТИСТИКИ
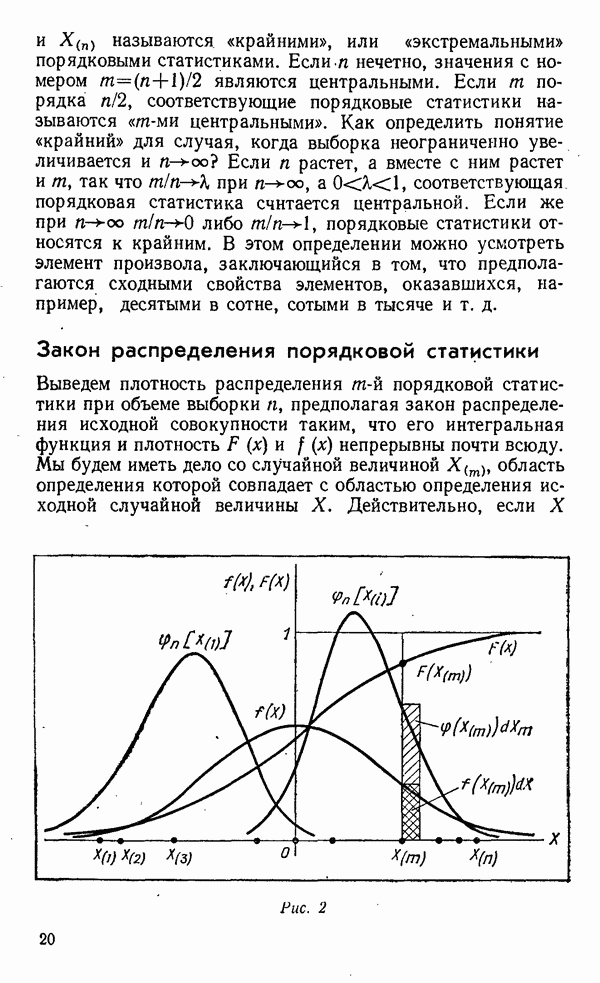
- Закон распределения порядковой статистики
- Числовые характеристики порядковой статистики
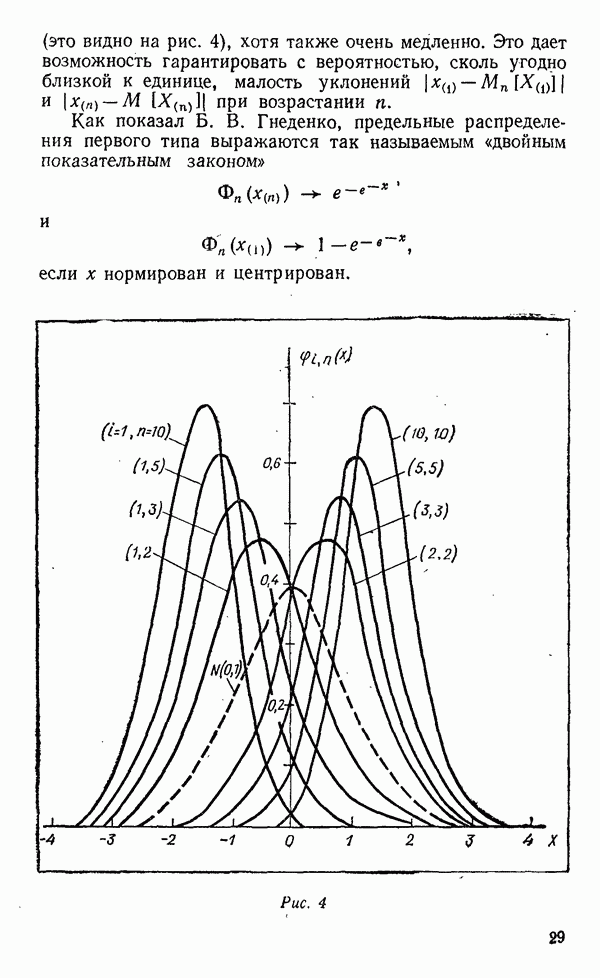
- Распределения при неограниченном увеличении выборки. Распределения центральных значений
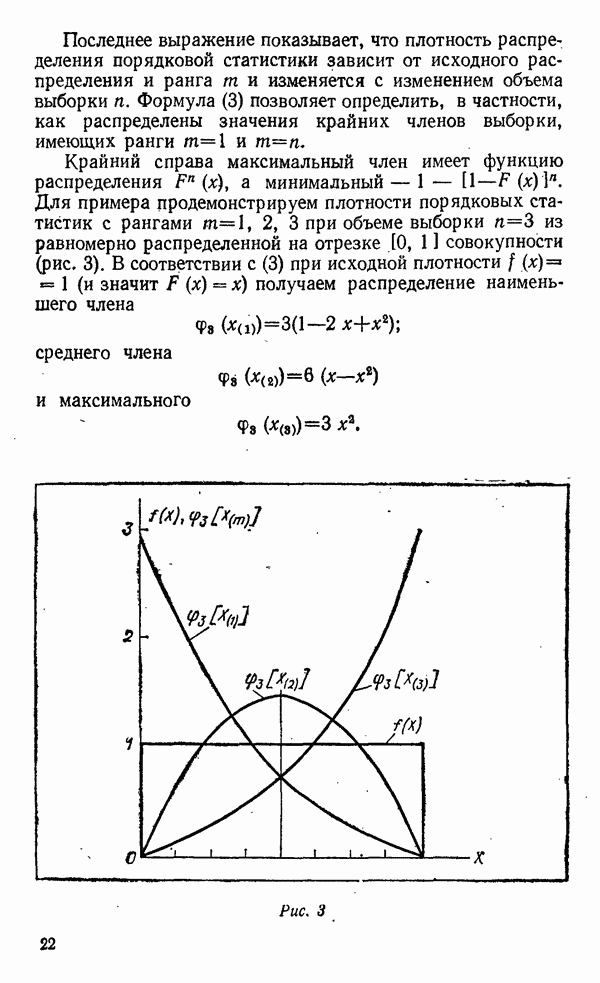
- Распределения крайних значений
- Совместные распределения порядковых статистик
- 3. ВЫБОРОЧНЫЕ ЗНАЧЕНИЯ И РАНГИ
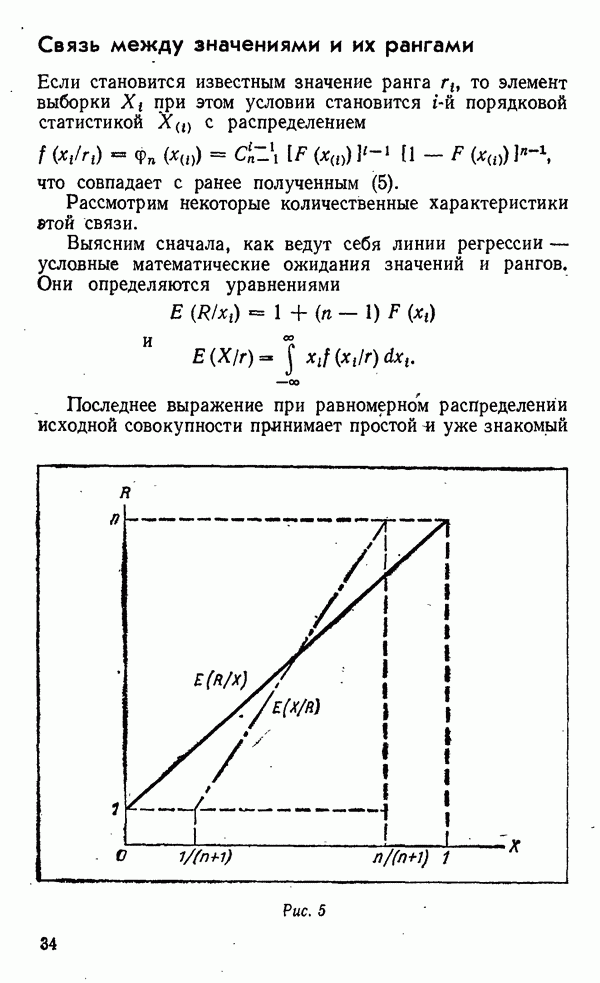
- Связь между значениями и их рангами
- Ранговая корреляция
- 4. УЛУЧШЕНИЕ ОЦЕНОК ПУТЕМ ЦЕНЗУРИРОВАНИЯ ВЫБОРОК
- Цензурирование выборок — общая идея
- Оценки параметров нормального распределения по усеченным выборкам
- Оценки параметров равномерного распределения
- Выборка из трех наблюдений
- 5. БЕЗЭТАЛОННЫЕ ПРОЦЕДУРЫ ИЗМЕРЕНИЯ, ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИИ
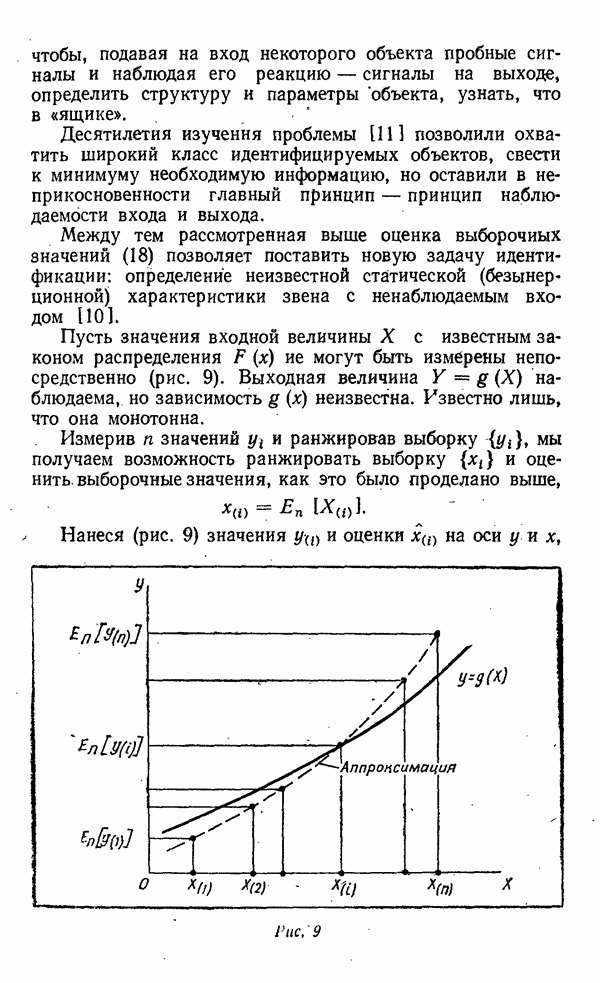
- Идентификация объекта с ненаблюдаемым входом
- Безэталонная классификация
- ЛИТЕРАТУРА