| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
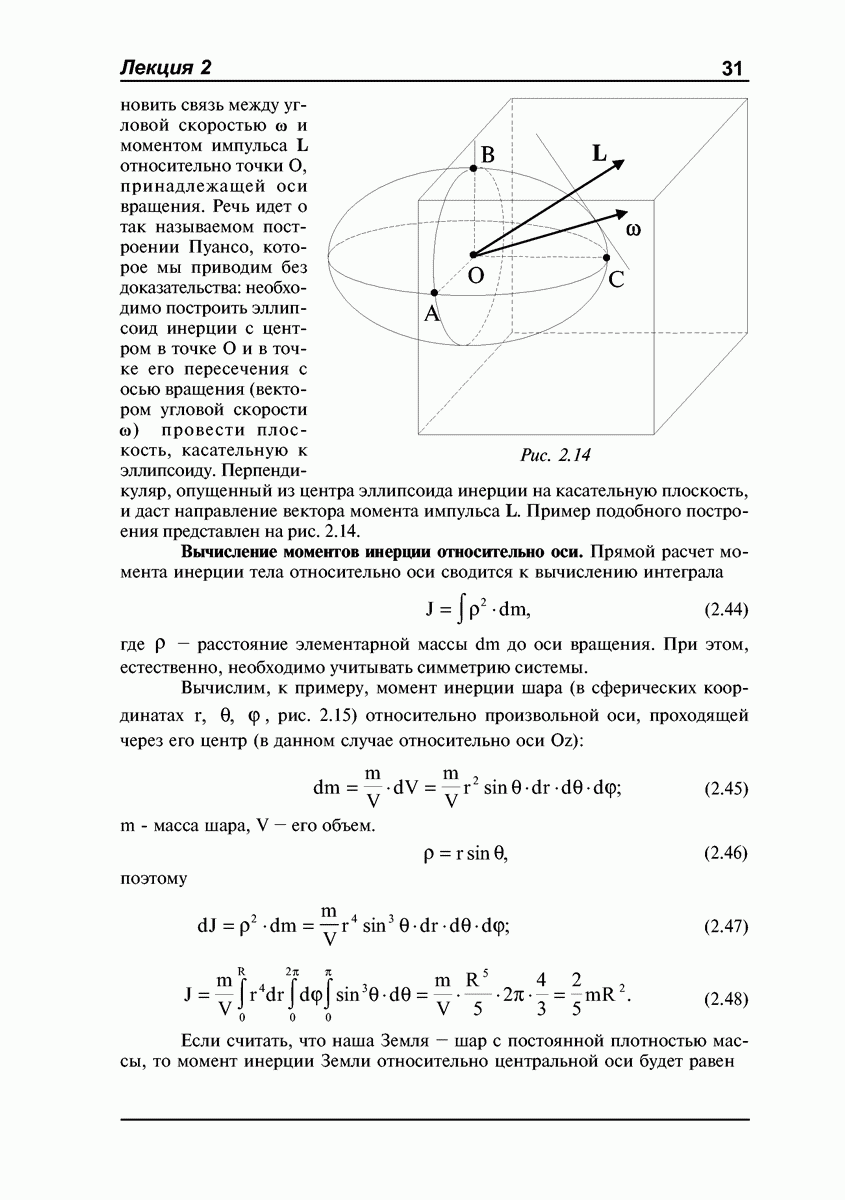
Момент импульса твердого тела относительно оси. Момент инерции относительно оси.
В тех случаях, когда твердое тело вращается вокруг неподвижной оси, обычно оперируют с понятиями момента импульса и момента инерции относительно оси. Момент импульса  относительно оси — это проекция на данную ось момента импульса
относительно оси — это проекция на данную ось момента импульса  определенного относительно некоторой точки О, принадлежащей оси, причем, как оказывается, выбор точки О на оси значения не имеет.
определенного относительно некоторой точки О, принадлежащей оси, причем, как оказывается, выбор точки О на оси значения не имеет.
Действительно, при вычислении  существенно лишь плечо импульса
существенно лишь плечо импульса  относительно оси вращения
относительно оси вращения  (рис. 2.12), то есть кратчайшее расстояние
(рис. 2.12), то есть кратчайшее расстояние  массы
массы  до оси:
до оси:

Здесь учтено, что скорость массы  при вращательном движении
при вращательном движении 

Рис. 2.12
Рассмотрим эту ситуацию более подробно. Пусть оси  на рис. 2.12 — главные оси инерции для точки
на рис. 2.12 — главные оси инерции для точки  — неподвижная в лабораторной системе ось вращения, жестко связанная с телом. Вектор угловой скорости
— неподвижная в лабораторной системе ось вращения, жестко связанная с телом. Вектор угловой скорости  направленный вдоль
направленный вдоль  можно разложить по осям системы координат
можно разложить по осям системы координат 

где  — направляющие косинусы оси
— направляющие косинусы оси  Вектор
Вектор  не совпадает с
не совпадает с  и при вращении тела описывает коническую поверхность, симметричную относительно
и при вращении тела описывает коническую поверхность, симметричную относительно  Вектор
Вектор  также можно разложить по осям системы
также можно разложить по осям системы  причем
причем

где  — главные моменты инерции.
— главные моменты инерции.
Проекция вектора  на ось вращения, или, что то же самое, момент импульса относительно оси
на ось вращения, или, что то же самое, момент импульса относительно оси

где

— момент инерции относительно оси.
Последняя формула позволяет рассчитать момент инерции твердого тела относительно произвольной оси в том случае, если известны главные моменты инерции  и ориентация оси вращения относительно главных осей инерции (углы
и ориентация оси вращения относительно главных осей инерции (углы  Во многих случаях такое вычисление оказывается значительно проще, чем прямой расчет по формуле
Во многих случаях такое вычисление оказывается значительно проще, чем прямой расчет по формуле

(см. (2.31)).
Отметим, что, в соответствии с данным выше определением,  — величина скалярная (проекция вектора
— величина скалярная (проекция вектора  на ось вращения). Вместе с тем можно говорить и о векторе
на ось вращения). Вместе с тем можно говорить и о векторе  рассматривая его как составляющую вектора
рассматривая его как составляющую вектора  вдоль оси:
вдоль оси:

(вектор Р; изображен на рис.  . В рекомендуемых учебных пособиях можно встретить обе трактовки понятия момента импульса относительно оси.
. В рекомендуемых учебных пособиях можно встретить обе трактовки понятия момента импульса относительно оси.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- ЛЕКЦИЯ №1. Кинематика абсолютно твердого тела. Степени свободы. Углы Эйлера. Поступательное движение. Вращение вокруг неподвижной оси. Плоское движение. Движение твердого тела, имеющего одну неподвижную точку. Движение свободного твердого тела.
- Поступательное движение
- Вращение вокруг неподвижной оси
- Плоское движение
- Движение твердого тела с одной неподвижной точкой.
- Движение свободного твердого тела.
- ЛЕКЦИЯ №2. Динамика абсолютно твердого тела. Момент импульса. Тензор инерции. Момент импульса тела относительно оси. Эллипсоид инерции. Вычисление моментов инерции относительно оси. Теорема Гюйгенса-Штейнера. Момент импульса относительно движущегося центра масс.
- Главные оси инерции.
- Момент импульса твердого тела относительно оси. Момент инерции относительно оси.
- Эллипсоид инерции.
- Вычисление моментов инерции относительно оси.
- Теорема Гюйгенса-Штейнера.
- Момент импульса тела относительно движущегося центра масс.
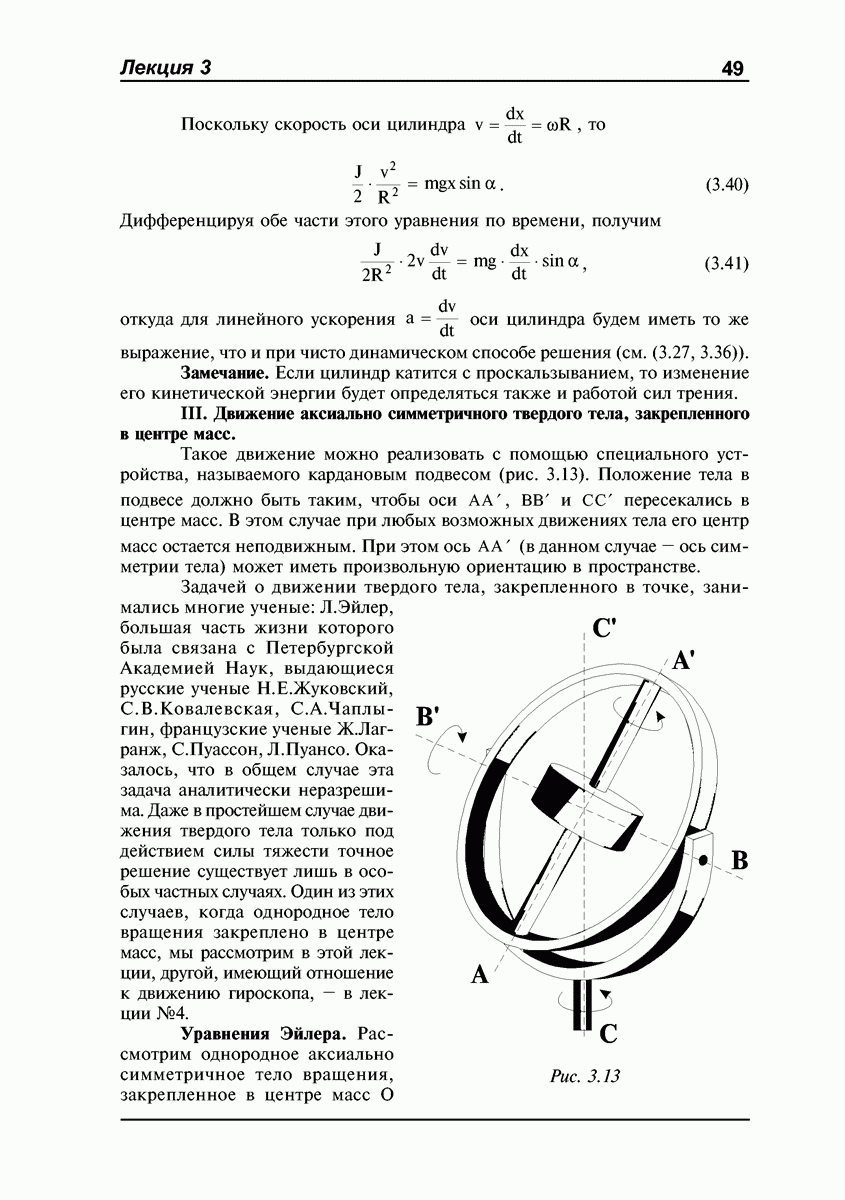
- ЛЕКЦИЯ №3. Динамика абсолютно твердого тела. Уравнение поступательного движения и уравнение моментов. Вращение твердого тела вокруг неподвижной оси. Центр удара. Динамика плоского движения твердого тела. Движение аксиально симметричного твердого тела, закрепленного в центре масс. Уравнения Эйлера.
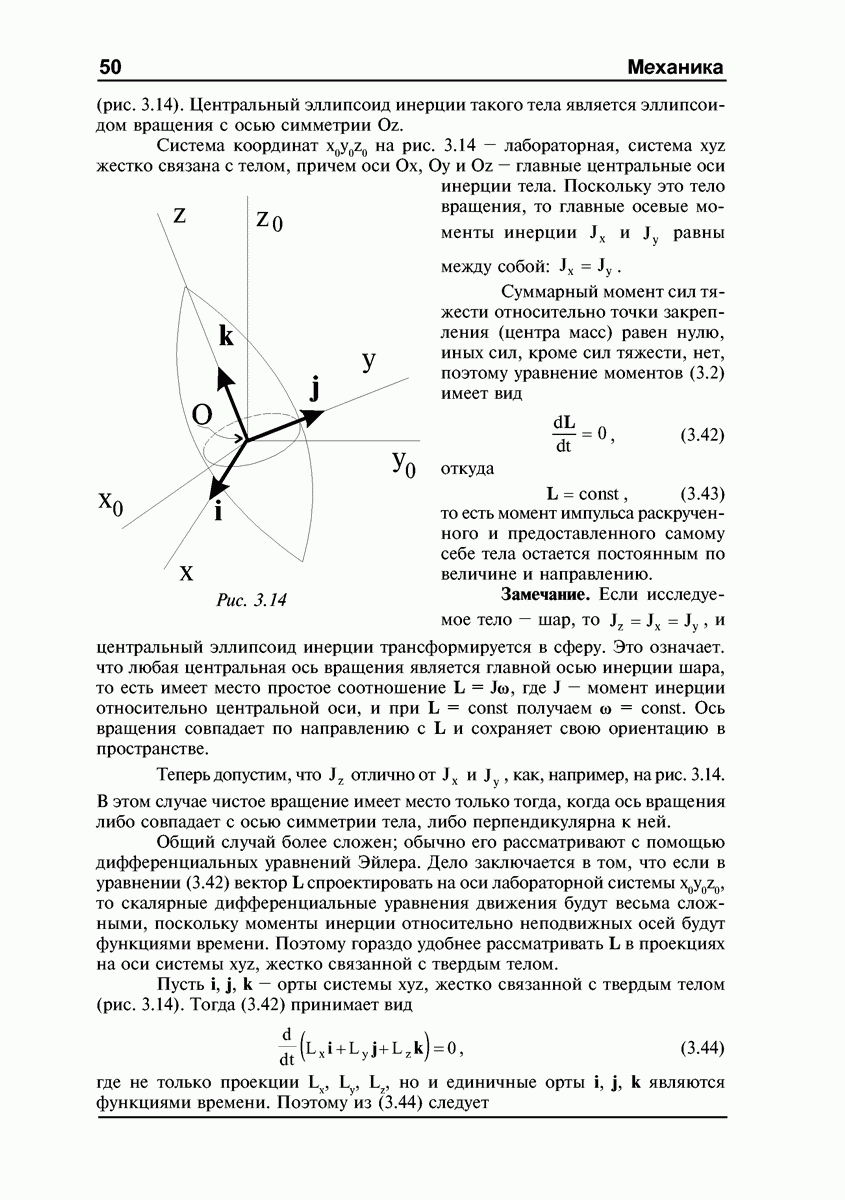
- Уравнения динамики твердого тела. Общий случай.
- Кинетическая энергия вращающегося тела и работа внешних сил (ось вращения неподвижна).
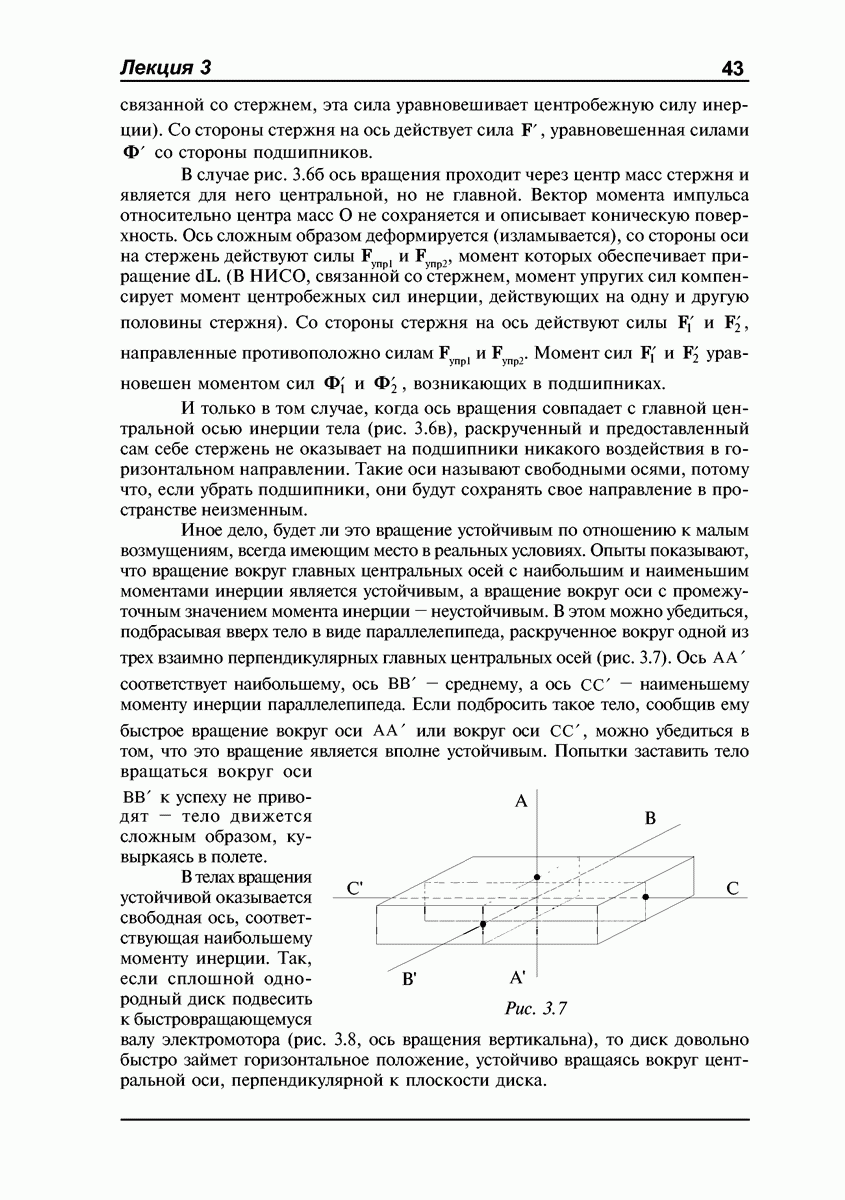
- Свободные оси. Устойчивость свободного вращения.
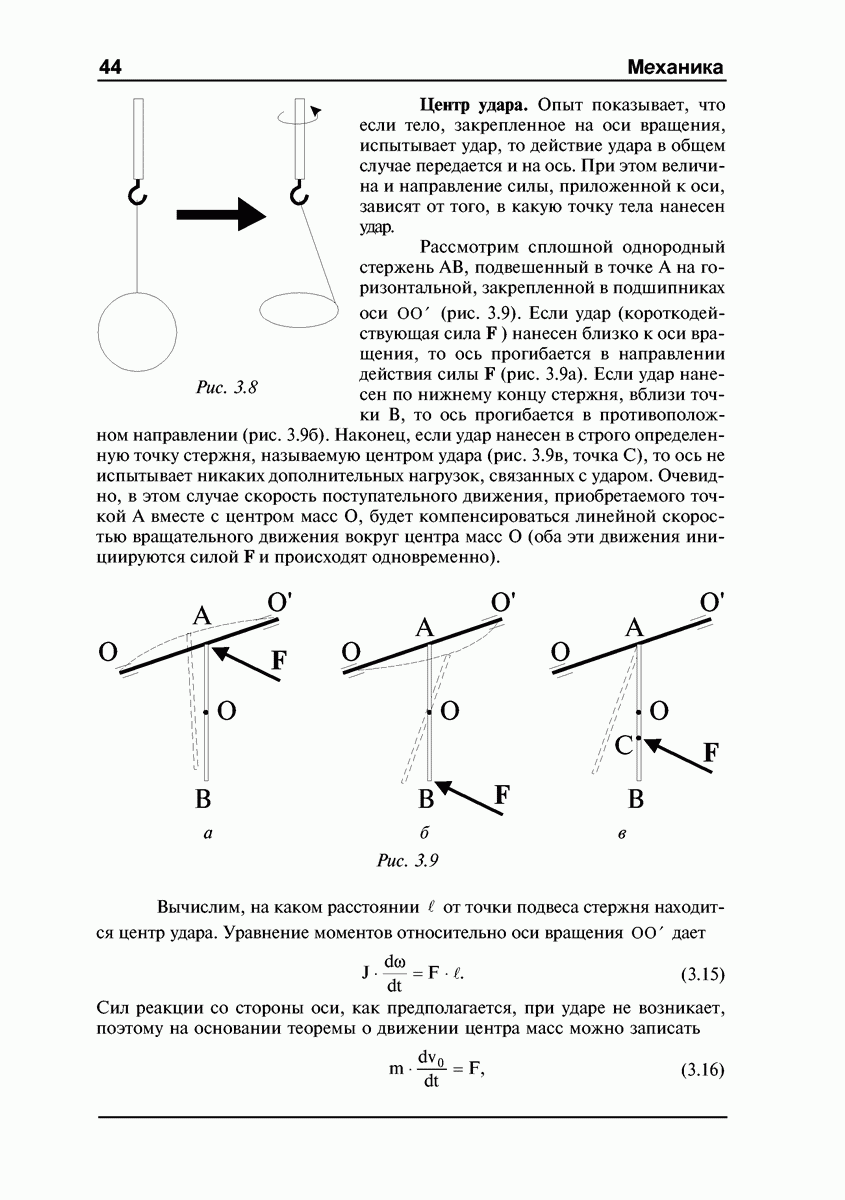
- Центр удара.
- Кинетическая энергия при плоском движении.
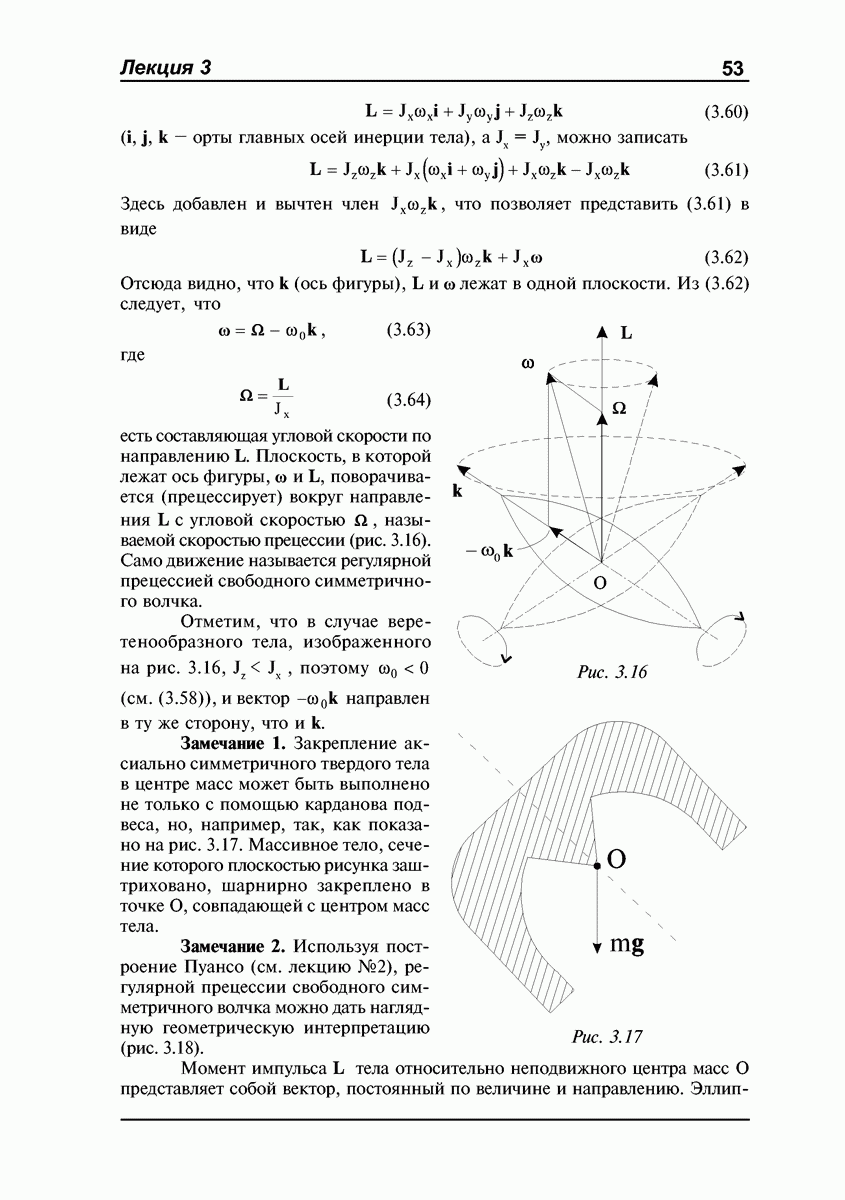
- Уравнения Эйлера.
- ЛЕКЦИЯ №4. Гироскопы. Свободный гироскоп. Прецессия гироскопа под действием внешних сил. Угловая скорость прецессии. Нутации. Гироскопические силы, их природа и проявления.
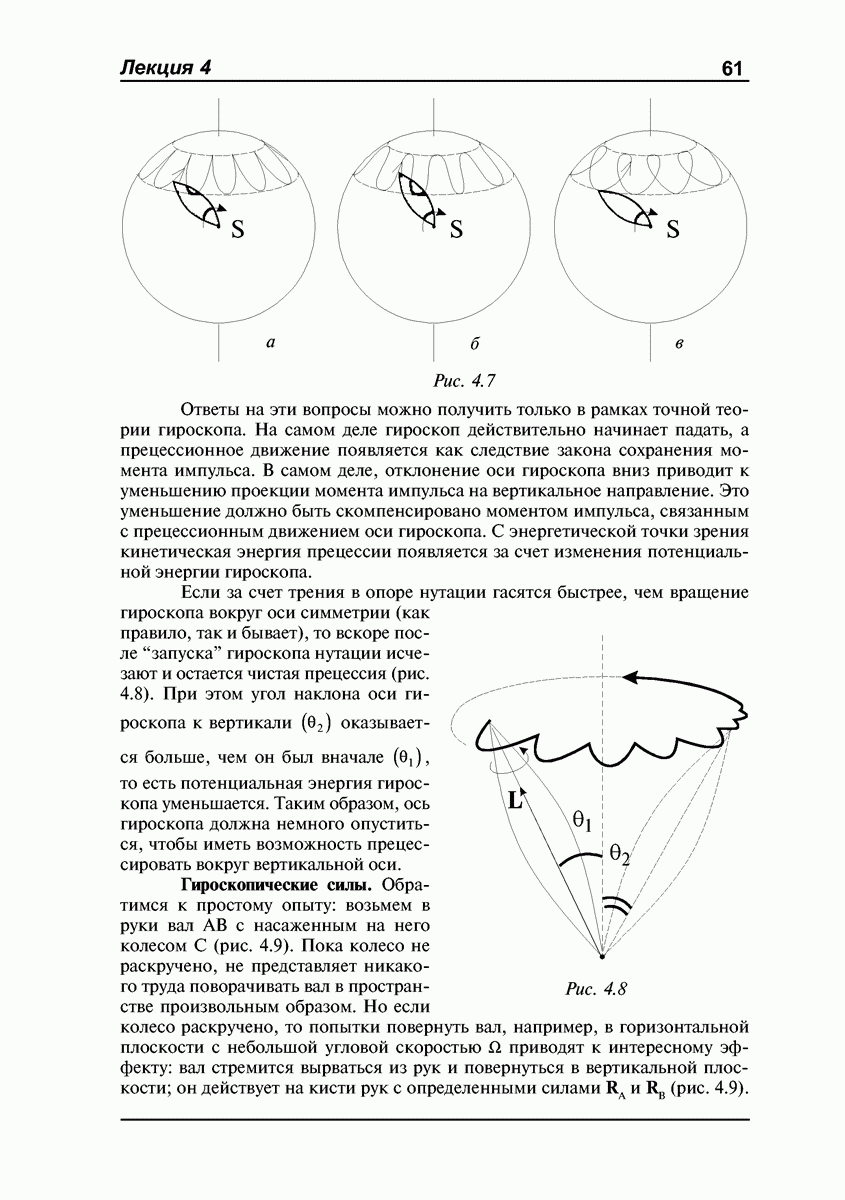
- Свободный гироскоп.
- Прецессия гироскопа под действием внешних сил. Элементарная теория.
- Прецессия гироскопа под действием внешних сил. Отход от элементарной теории. Нутации.
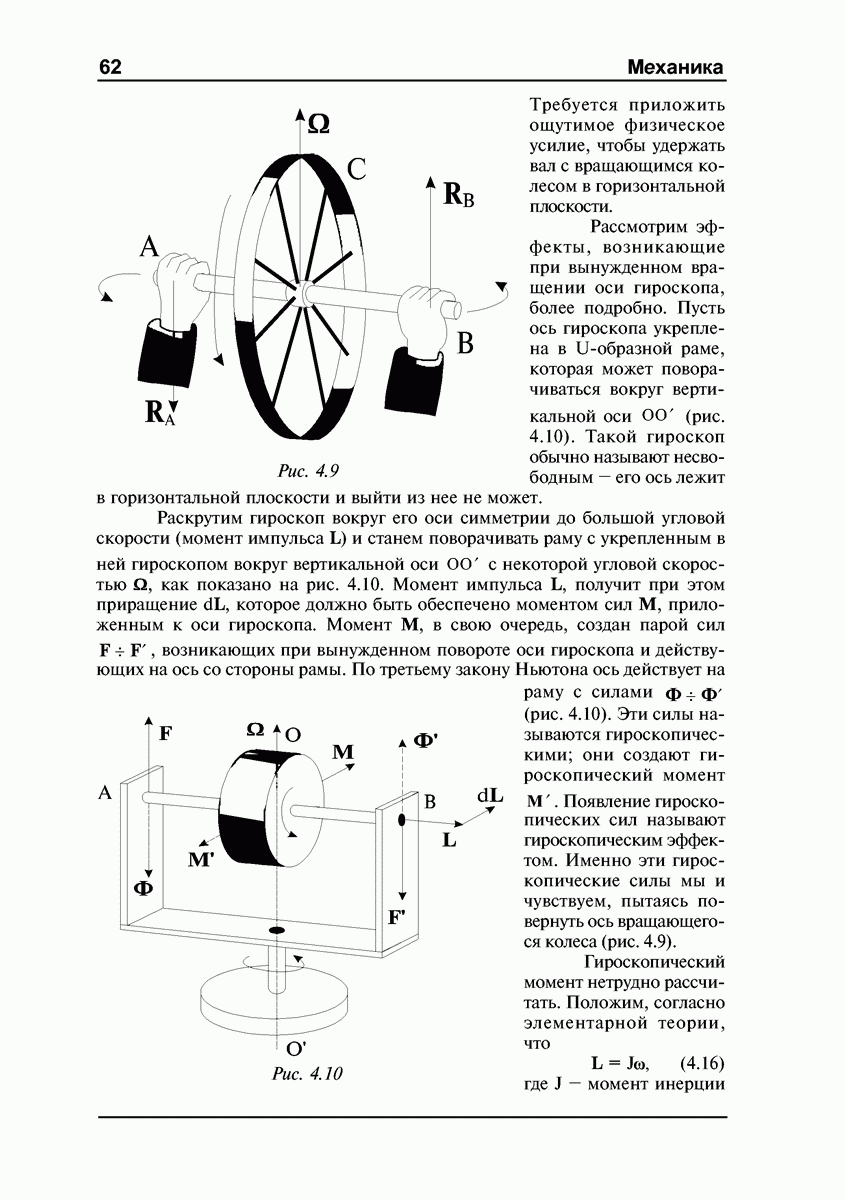
- Гироскопические силы.
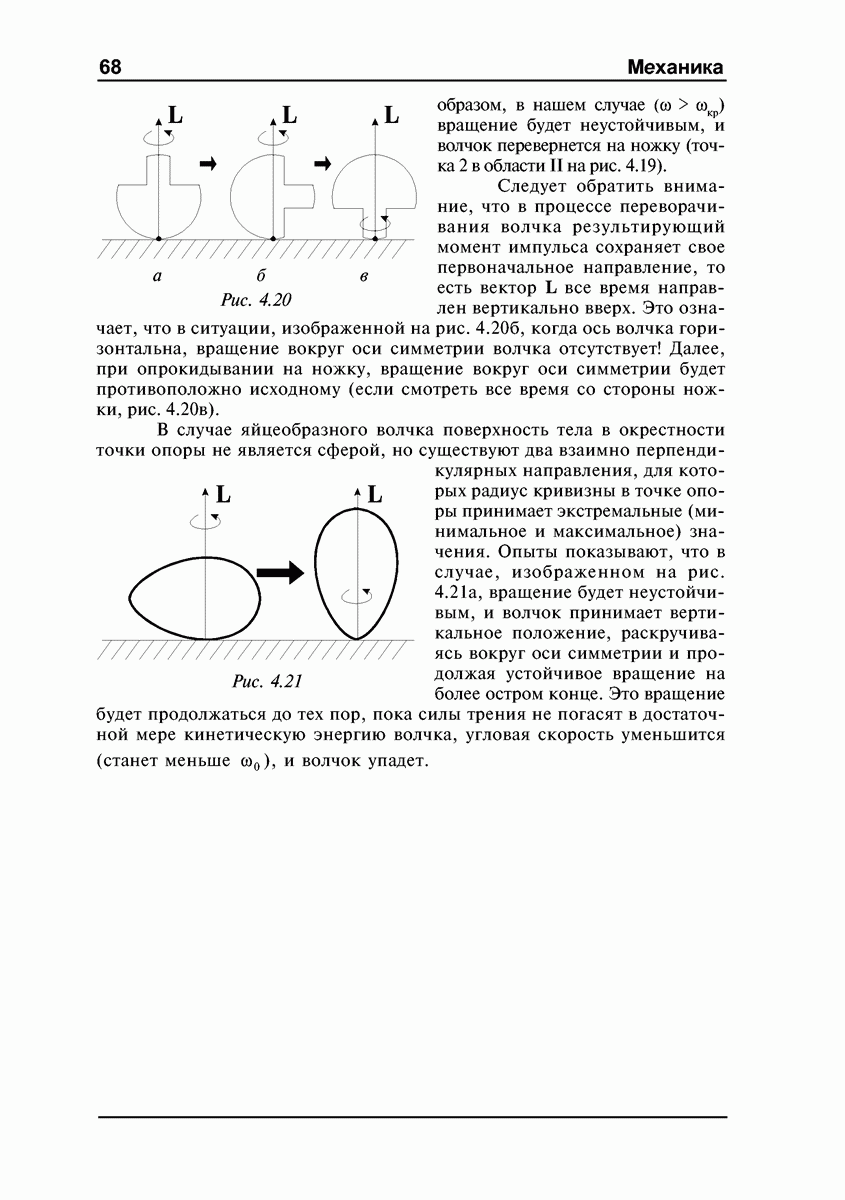
- Волчки.
- ЛИТЕРАТУРА