| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
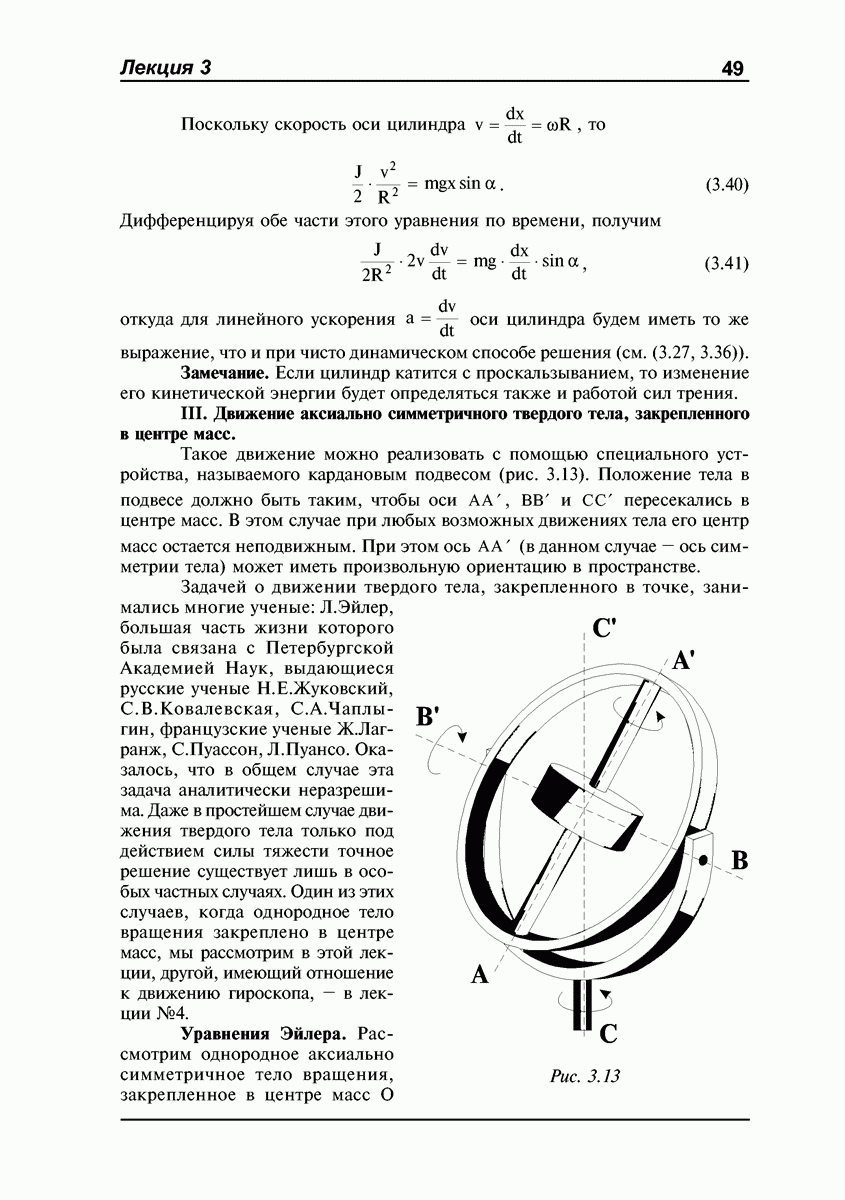
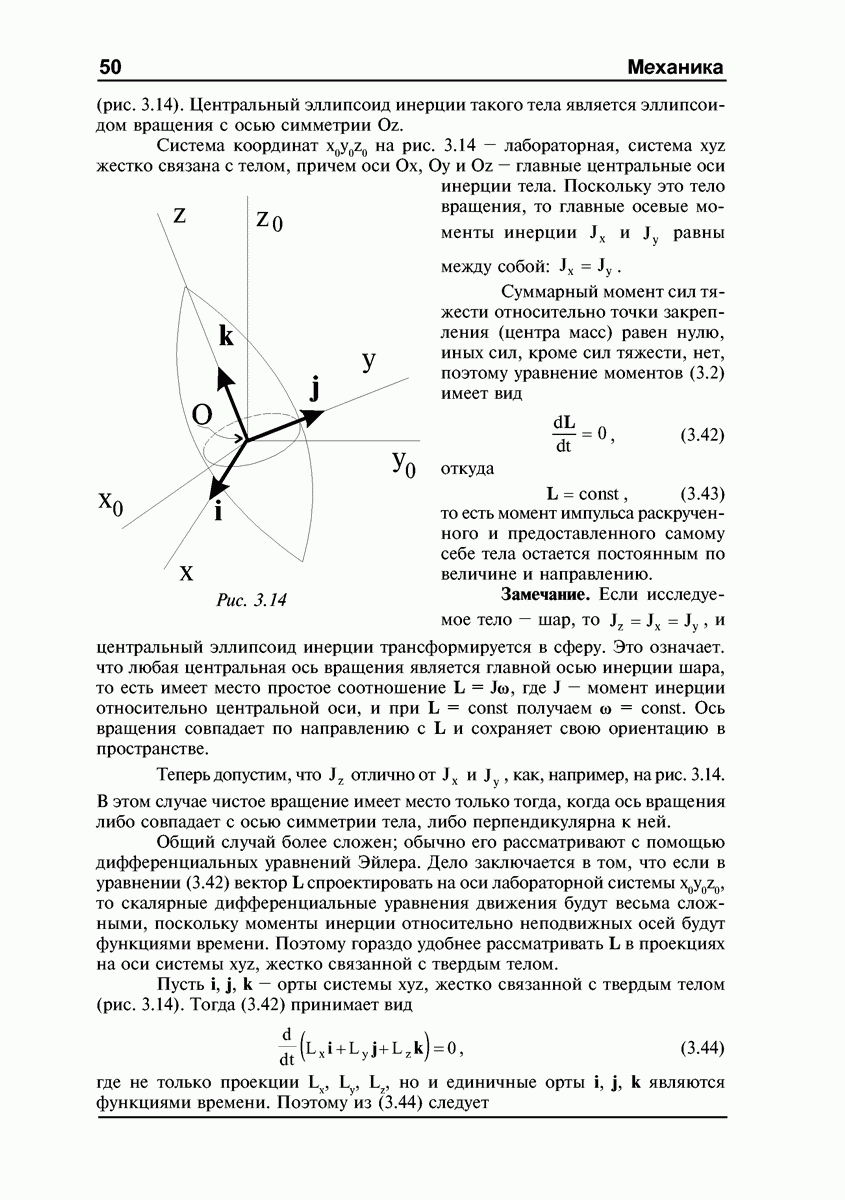
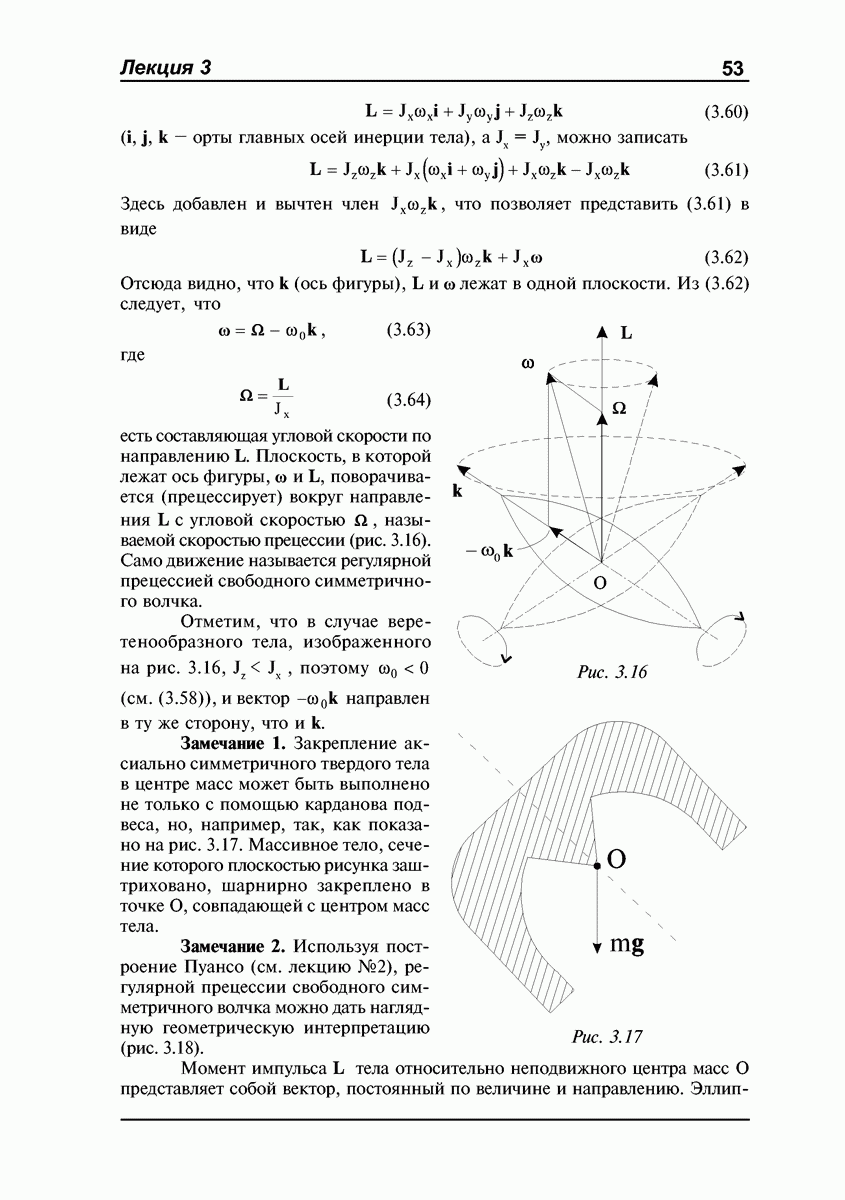
ЛЕКЦИЯ №2. Динамика абсолютно твердого тела. Момент импульса. Тензор инерции. Момент импульса тела относительно оси. Эллипсоид инерции. Вычисление моментов инерции относительно оси. Теорема Гюйгенса-Штейнера. Момент импульса относительно движущегося центра масс.
Задача динамики абсолютно твердого тела — изучить движение тела в зависимости от действующих на него сил. Как следует из предыдущего рассмотрения, произвольное движение твердого тела можно свести к поступательному и вращательному. При поступательном движении траектории всех точек тела одинаковы, и для описания этого движения используются такие понятия, как масса, импульс, сила. При изучении вращательного движения тела этих понятий оказывается недостаточно.
Рассмотрим два цилиндра одинаковой массы и одинаковых размеров, причем один цилиндр, изготовленный из более легкого материала, пусть будет сплошным, а другой, изготовленный из более тяжелого материала, — полым. Опыт показывает, что при соскальзывании с достаточно гладкой наклонной плоскости цилиндры не вращаются и ведут себя совершенно одинаково (рис. 2.1а); в частности, они одновременно достигают основания этой наклонной плоскости. Иное дело, если плоскость шероховатая, и цилиндры скатываются, вращаясь вокруг своей оси (рис. 2.16), — в этом случае быстрее скатывается сплошной цилиндр. Таким образом, при вращательном движении существенно распределение массы относительно оси вращения.
Об этом же свидетельствуют и другие опыты: чем дальше от оси вращения сосредоточена масса тела, тем труднее его раскрутить при воздействии постоянной силой, имеющей одно и то же плечо (рис. 2.2 а,б). Для раскручивания стержней с грузами до угловой скорости  в случае рис. 2.26 требуется большее время, чем в случае рис. 2.2а. В этих же опытах можно показать, что при вращательном движении тела существенную роль играет не сама сила, а ее момент: если перебросить нить на шкив большего радиуса, то раскрутить эти тела
в случае рис. 2.26 требуется большее время, чем в случае рис. 2.2а. В этих же опытах можно показать, что при вращательном движении тела существенную роль играет не сама сила, а ее момент: если перебросить нить на шкив большего радиуса, то раскрутить эти тела

Рис. 2.1

Рис. 2.2
будет легче (рис. 2.2в). Таким образом, для описания вращательного движения тела необходимо ввести новые понятия: момент инерции, момент импульса, момент силы.
Момент импульса. Тензор инерции.
Момент импульса тела относительно неподвижной точки — важнейшее понятие в динамике вращательного движения твердого тела. Он определяется так же, как и для системы материальных точек:

Здесь  — импульс элементарной массы
— импульс элементарной массы  в лабораторной системе
в лабораторной системе  а
а  — радиус-вектор массы
— радиус-вектор массы  началом в той неподвижной точке, относительно которой вычисляется момент импульса тела.
началом в той неподвижной точке, относительно которой вычисляется момент импульса тела.
С учетом постоянства расстояний между точками абсолютно твердого тела вектор момента импульса  удается связать с вектором угловой скорости
удается связать с вектором угловой скорости  .
.
Рассмотрим, к примеру, две одинаковые точечные массы  укрепленные на концах невесомого стержня
укрепленные на концах невесомого стержня  (рис. 2.3). Стержень с массами вращается с угловой скоростью
(рис. 2.3). Стержень с массами вращается с угловой скоростью  вокруг вертикальной оси, проходящей через середину стержня и перпендикулярной ему. В этом случае
вокруг вертикальной оси, проходящей через середину стержня и перпендикулярной ему. В этом случае

Здесь учтено, что  .
.
Существенно, что в этом примере вектор  направлен так же, как и
направлен так же, как и  . К сожалению, так бывает не всегда. В этом можно убедиться на примере, показанном на рис. 2.4. Здесь невесомый стержень
. К сожалению, так бывает не всегда. В этом можно убедиться на примере, показанном на рис. 2.4. Здесь невесомый стержень  с двумя массами
с двумя массами  на концах жестко закреплен на вертикальной оси (в точке О) под некоторым углом а к ней и лежит в плоскости
на концах жестко закреплен на вертикальной оси (в точке О) под некоторым углом а к ней и лежит в плоскости  При вращении стержня вокруг вертикальной оси с угловой скоростью
При вращении стержня вокруг вертикальной оси с угловой скоростью  вектор
вектор  определенный по (2.1), будет находиться в плоскости
определенный по (2.1), будет находиться в плоскости  и составит угол
и составит угол  с осью
с осью  . Система
. Система  введенная в начале лекции 1, жестко связана со стержнем и поворачивается вместе с ним. При этом вектор
введенная в начале лекции 1, жестко связана со стержнем и поворачивается вместе с ним. При этом вектор  остается в плоскости
остается в плоскости  а в лабораторной системе движется по конической поверхности с углом полураствора
а в лабораторной системе движется по конической поверхности с углом полураствора 
Получим выражение для  в случае твердого тела произвольной формы, закрепленного в некоторой точке О.
в случае твердого тела произвольной формы, закрепленного в некоторой точке О.
Пусть  — радиус-вектор элементарной массы
— радиус-вектор элементарной массы  твердого тела, а
твердого тела, а  угловая скорость. Тогда
угловая скорость. Тогда

Рис. 2.3

Рис. 2.4

Векторы  и
и  можно проектировать как на оси лабораторной системы
можно проектировать как на оси лабораторной системы  так и на оси системы
так и на оси системы  жестко связанной с твердым телом (поскольку точка О неподвижна, начала обеих систем можно совместить). Преимущество системы
жестко связанной с твердым телом (поскольку точка О неподвижна, начала обеих систем можно совместить). Преимущество системы  заключается в том, что в ней проекции
заключается в том, что в ней проекции  являются постоянными величинами (в системе
являются постоянными величинами (в системе  они зависят от времени), и выражения для компонент
они зависят от времени), и выражения для компонент  оказываются проще.
оказываются проще.
Итак, в системе 

Тогда, продолжая (2.3), можно записать:

Выражения для проекций момента импульса на оси системы  запишем в следующем виде:
запишем в следующем виде:

или

где  компонент так называемого тензора инерции
компонент так называемого тензора инерции  твердого тела относительно точки О:
твердого тела относительно точки О:

Диагональные элементы тензора  называются осевыми моментами инерции, недиагональные элементы
называются осевыми моментами инерции, недиагональные элементы 
называются центробежными моментами инерции. Обратим внимание, что  Такой тензор называют симметричным.
Такой тензор называют симметричным.
Если координатам  и
и  присвоить номера 1, 2 и 3 соответственно, то (2.9-2.11) можно представить в виде
присвоить номера 1, 2 и 3 соответственно, то (2.9-2.11) можно представить в виде

В символическом виде можно записать так:

Самое главное, что стоит за приведенными выше формулами, заключается в следующем. Девять величин  (из них шесть независимых) определяют однозначную связь между
(из них шесть независимых) определяют однозначную связь между  и
и  причем оказывается, что
причем оказывается, что  вообще говоря, не совпадает по направлению с
вообще говоря, не совпадает по направлению с  (рис. 2.5).
(рис. 2.5).

Рис. 2.5
Итак, мы столкнулись с новым типом величин, имеющим важное значение в физике — тензором. Если для задания скалярной величины необходимо одно число (значение скалярной величины), векторной — три числа (три проекции вектора на оси декартовой системы координат), то для задания тензора необходимы в общем случае 9 чисел. На языке математики тензор — это многокомпонентная величина, характеризующаяся определенным поведением при преобразованиях системы координат (в данном случае компоненты тензора инерции преобразуются как произведения соответствующих координат).
Необходимость введения тензорных величин связана с различного рода анизотропией свойств физических макроскопических объектов. Тензор связывает две векторные величины, которые пропорциональны друг другу по модулю, но в силу анизотропии свойств объекта не совпадают друг с другом по направлению. В случае  и
и  решающую роль играет “анизотропия” формы тела (отсутствие определенной симметрии относительно осей
решающую роль играет “анизотропия” формы тела (отсутствие определенной симметрии относительно осей  ). В других случаях это может быть анизотропия, например, электрических или магнитных свойств вещества. Так, векторы поляризации вещества Р и напряженности электрического поля Е связаны тензором поляризуемости а:
). В других случаях это может быть анизотропия, например, электрических или магнитных свойств вещества. Так, векторы поляризации вещества Р и напряженности электрического поля Е связаны тензором поляризуемости а:  — электрическая постоянная). Это означает, что в силу анизотропии электрических свойств вещество поляризуется “не по полю”, то есть “не по полю” смещаются положительные и отрицательные заряды в молекулах вещества. Примерами других, в общем случае тензорных величин являются диэлектрическая проницаемость и магнитная проницаемость вещества. Важную роль в механике играют тензоры деформаций и напряжений. С этими и другими тензорными величинами вы познакомитесь при изучении соответствующих разделов курса общей физики.
— электрическая постоянная). Это означает, что в силу анизотропии электрических свойств вещество поляризуется “не по полю”, то есть “не по полю” смещаются положительные и отрицательные заряды в молекулах вещества. Примерами других, в общем случае тензорных величин являются диэлектрическая проницаемость и магнитная проницаемость вещества. Важную роль в механике играют тензоры деформаций и напряжений. С этими и другими тензорными величинами вы познакомитесь при изучении соответствующих разделов курса общей физики.
Замечание. Если  и
и  в выражении (2.3) проектировать на оси лабораторной системы
в выражении (2.3) проектировать на оси лабораторной системы  то компоненты тензора
то компоненты тензора  оказались бы
оказались бы
зависящими от времени. Такой подход в принципе возможен; он, в частности, используется в Берклеевском курсе физики [7].
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- ЛЕКЦИЯ №1. Кинематика абсолютно твердого тела. Степени свободы. Углы Эйлера. Поступательное движение. Вращение вокруг неподвижной оси. Плоское движение. Движение твердого тела, имеющего одну неподвижную точку. Движение свободного твердого тела.
- Поступательное движение
- Вращение вокруг неподвижной оси
- Плоское движение
- Движение твердого тела с одной неподвижной точкой.
- Движение свободного твердого тела.
- ЛЕКЦИЯ №2. Динамика абсолютно твердого тела. Момент импульса. Тензор инерции. Момент импульса тела относительно оси. Эллипсоид инерции. Вычисление моментов инерции относительно оси. Теорема Гюйгенса-Штейнера. Момент импульса относительно движущегося центра масс.
- Главные оси инерции.
- Момент импульса твердого тела относительно оси. Момент инерции относительно оси.
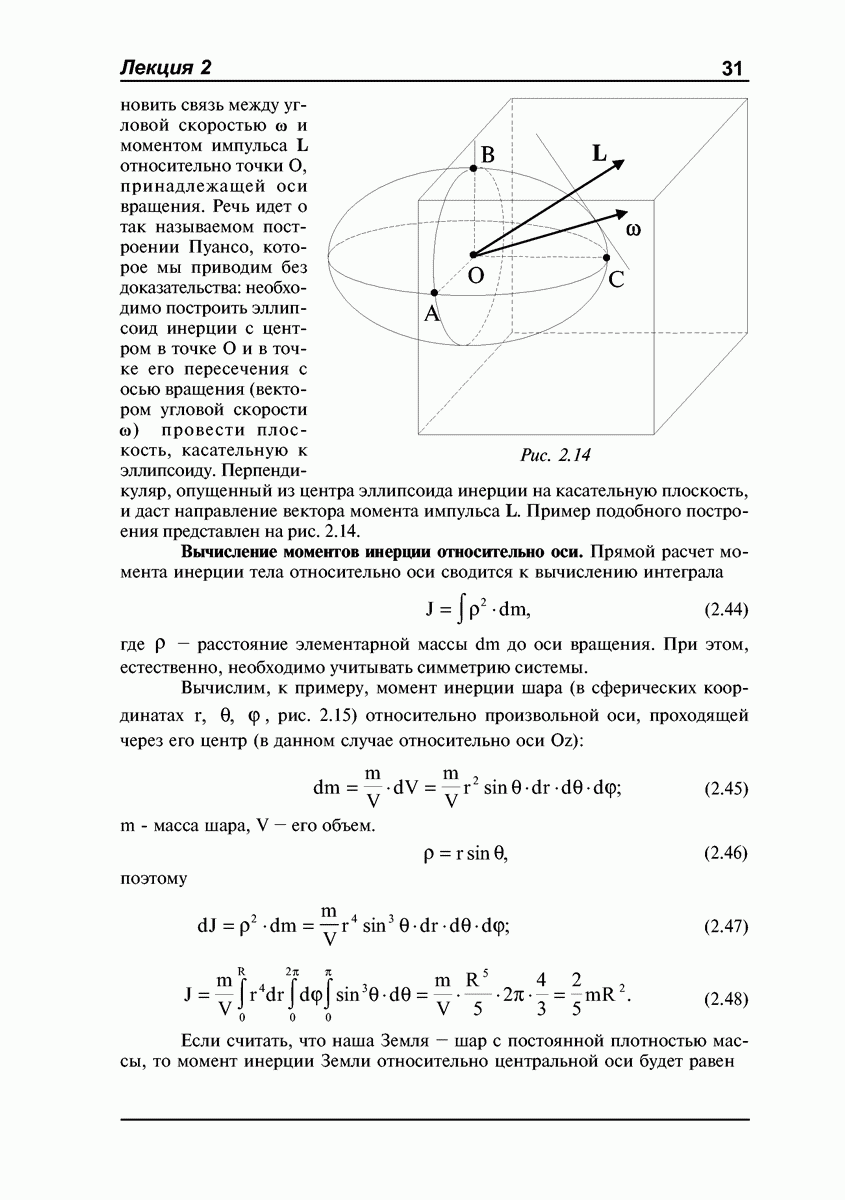
- Эллипсоид инерции.
- Вычисление моментов инерции относительно оси.
- Теорема Гюйгенса-Штейнера.
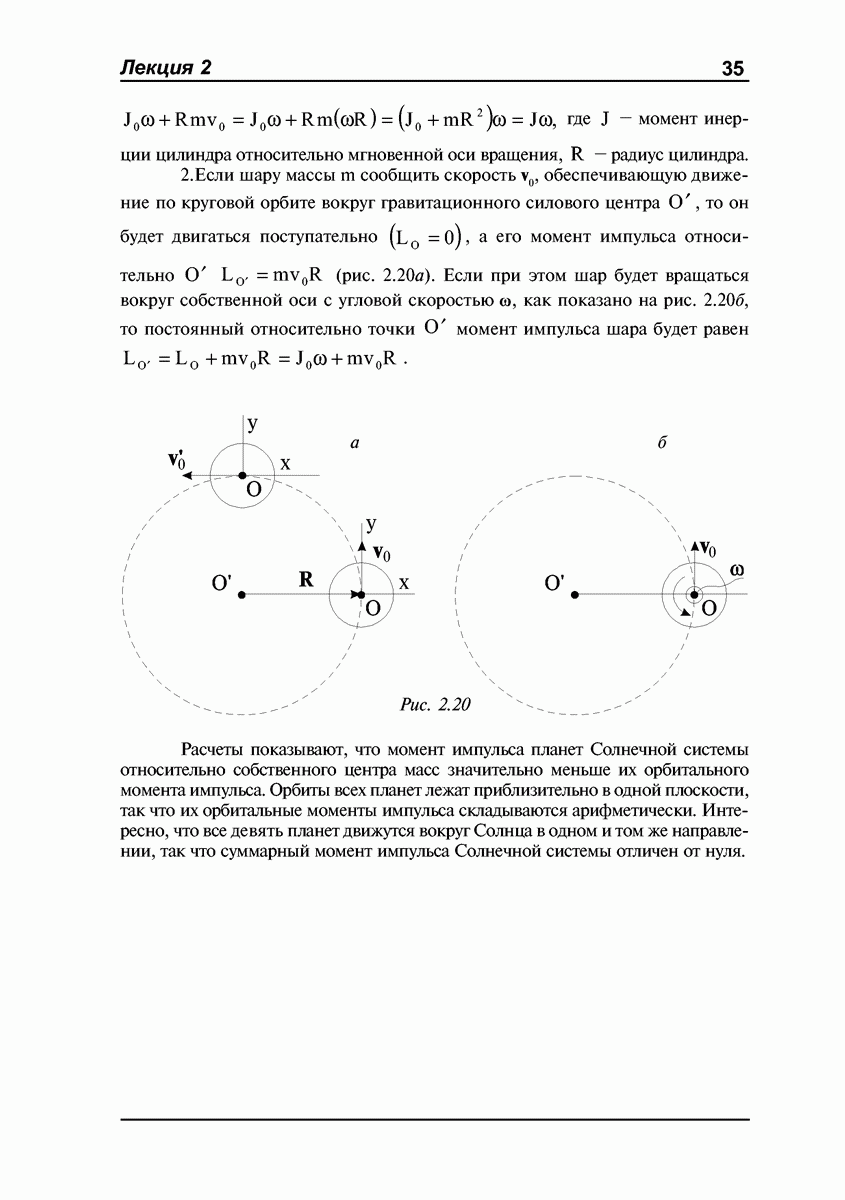
- Момент импульса тела относительно движущегося центра масс.
- ЛЕКЦИЯ №3. Динамика абсолютно твердого тела. Уравнение поступательного движения и уравнение моментов. Вращение твердого тела вокруг неподвижной оси. Центр удара. Динамика плоского движения твердого тела. Движение аксиально симметричного твердого тела, закрепленного в центре масс. Уравнения Эйлера.
- Уравнения динамики твердого тела. Общий случай.
- Кинетическая энергия вращающегося тела и работа внешних сил (ось вращения неподвижна).
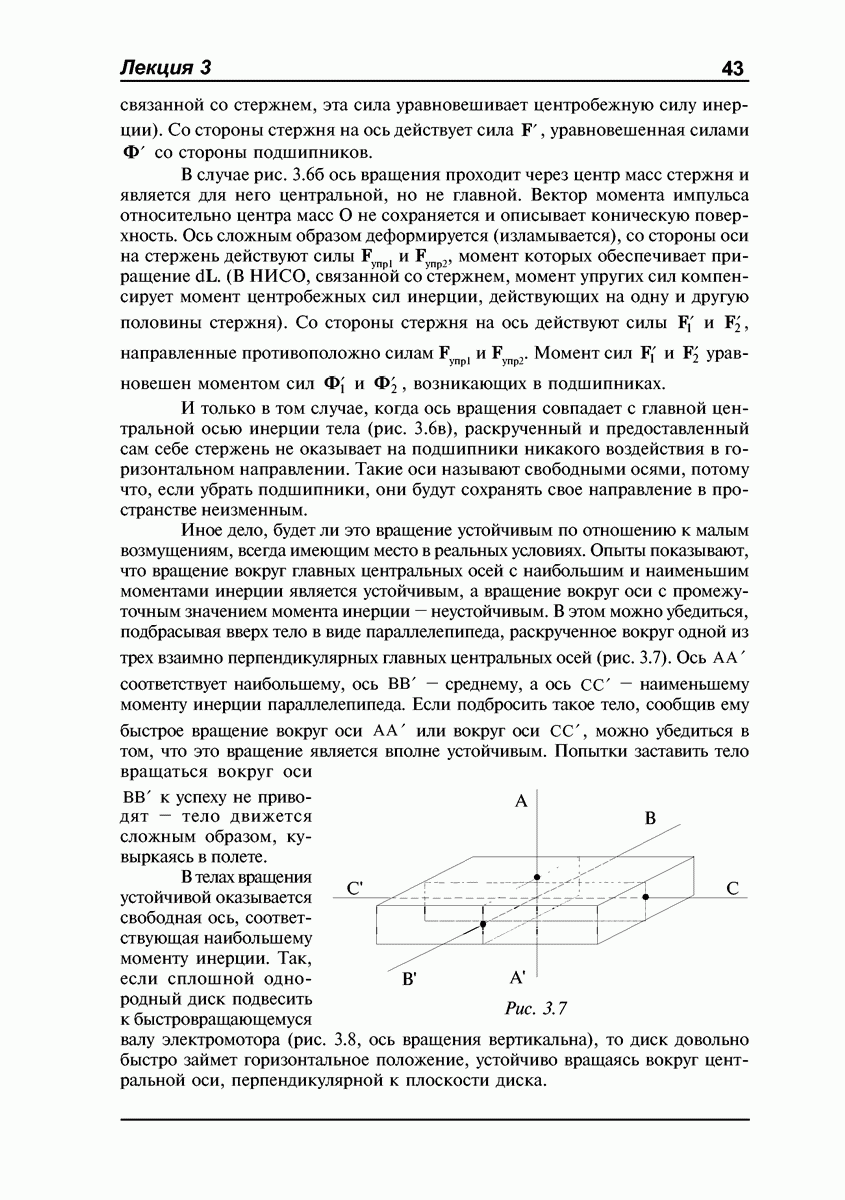
- Свободные оси. Устойчивость свободного вращения.
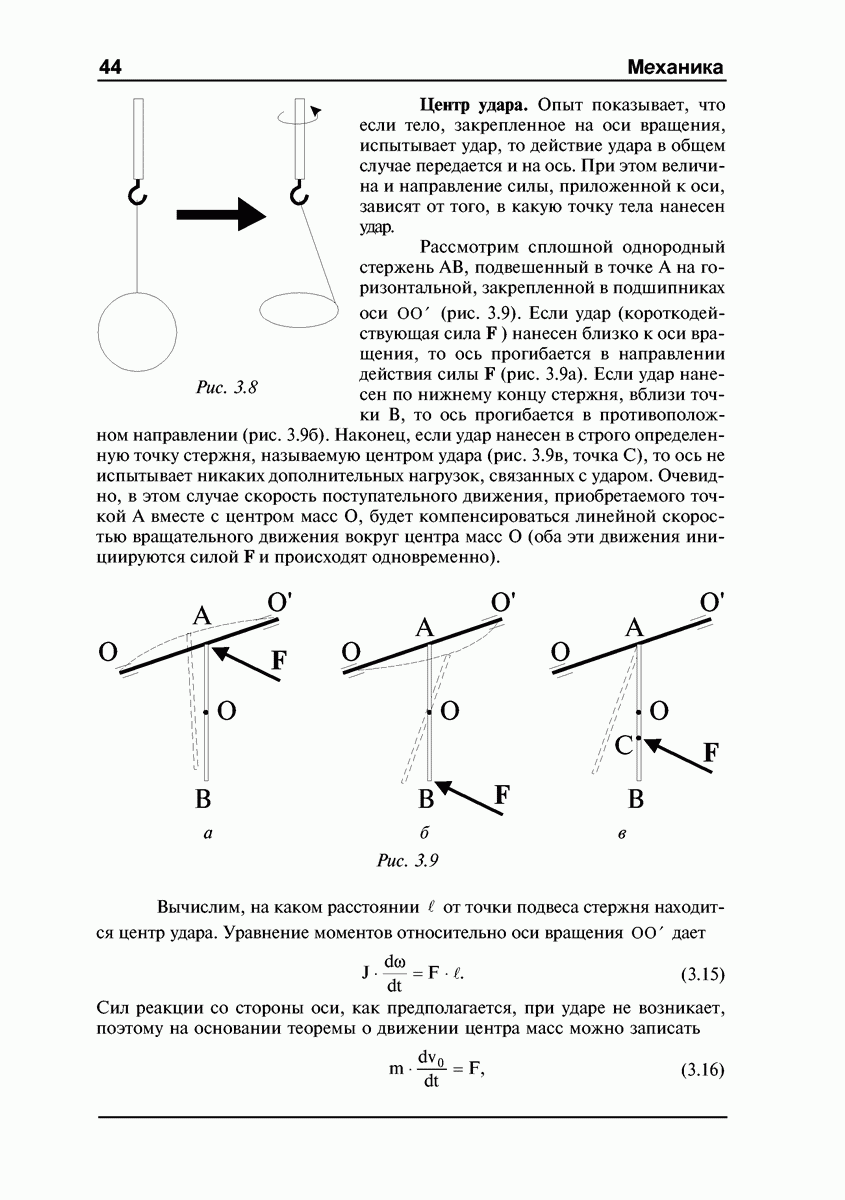
- Центр удара.
- Кинетическая энергия при плоском движении.
- Уравнения Эйлера.
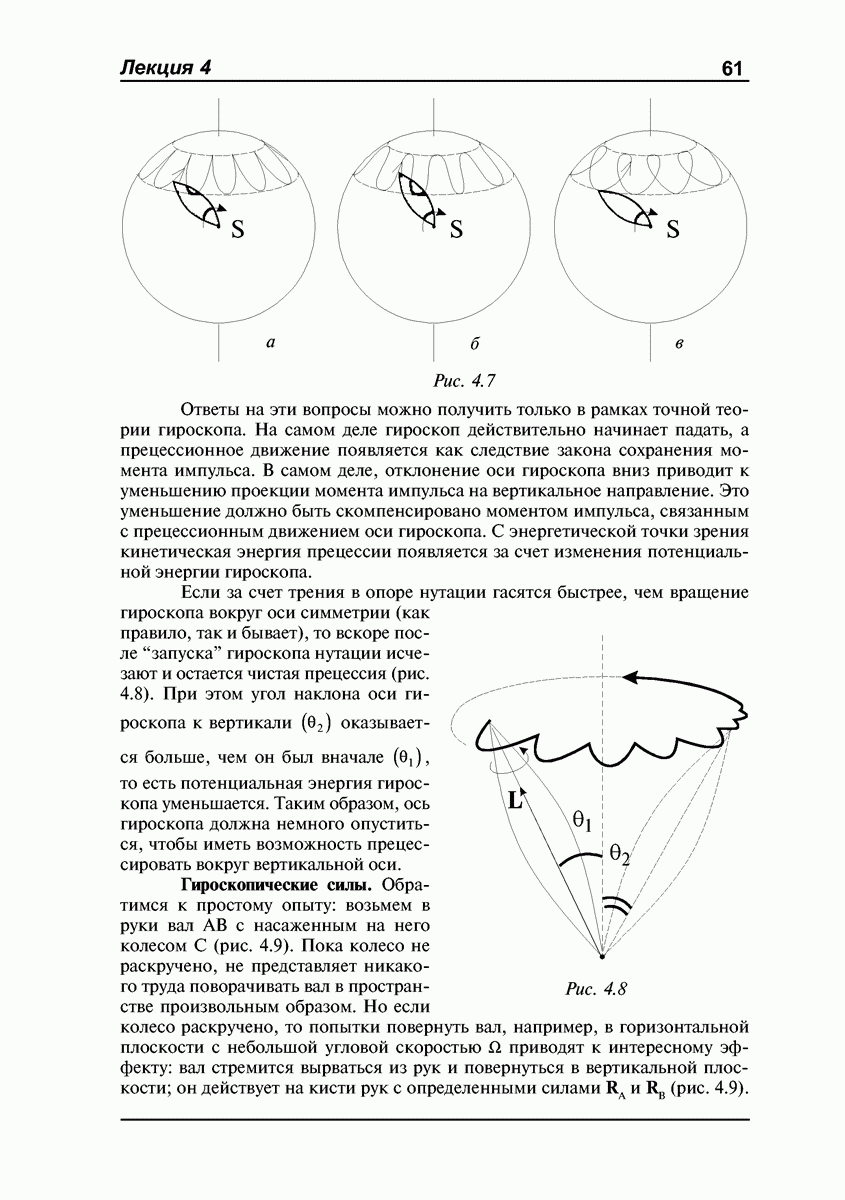
- ЛЕКЦИЯ №4. Гироскопы. Свободный гироскоп. Прецессия гироскопа под действием внешних сил. Угловая скорость прецессии. Нутации. Гироскопические силы, их природа и проявления.
- Свободный гироскоп.
- Прецессия гироскопа под действием внешних сил. Элементарная теория.
- Прецессия гироскопа под действием внешних сил. Отход от элементарной теории. Нутации.
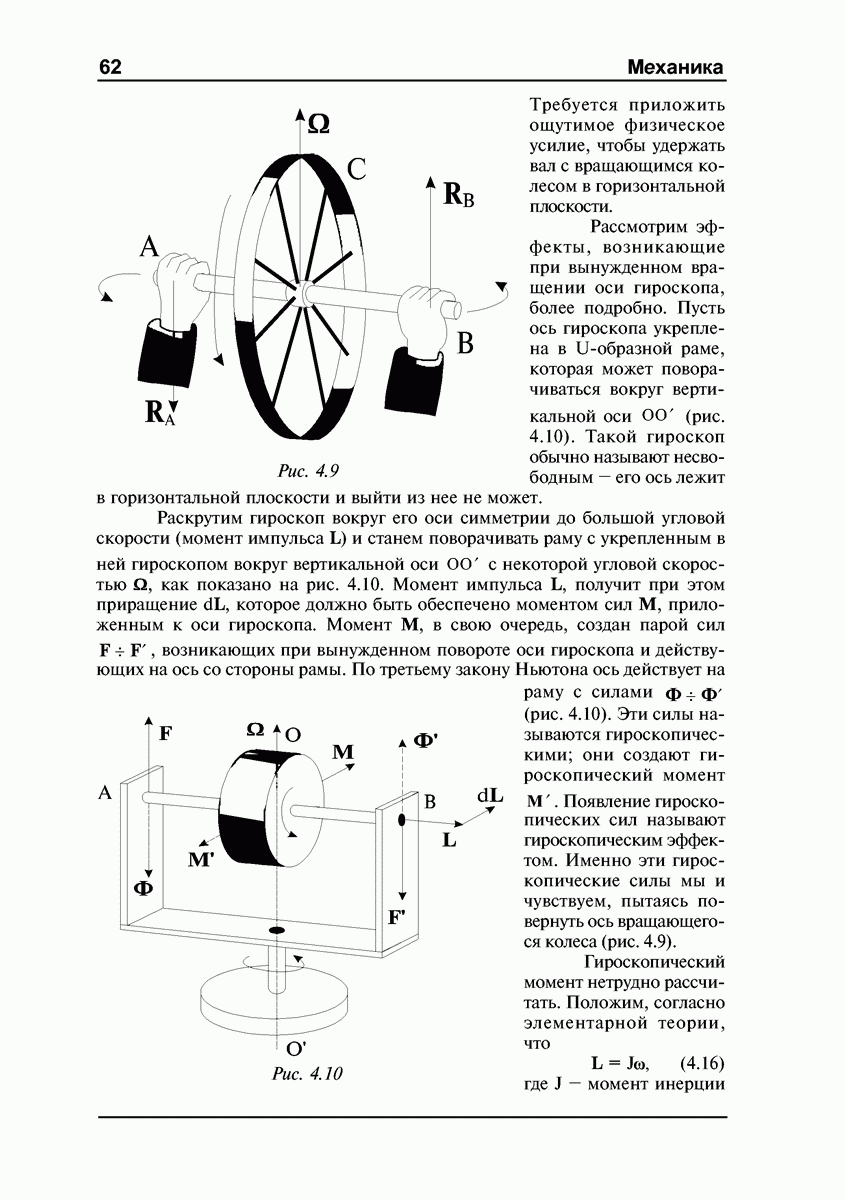
- Гироскопические силы.
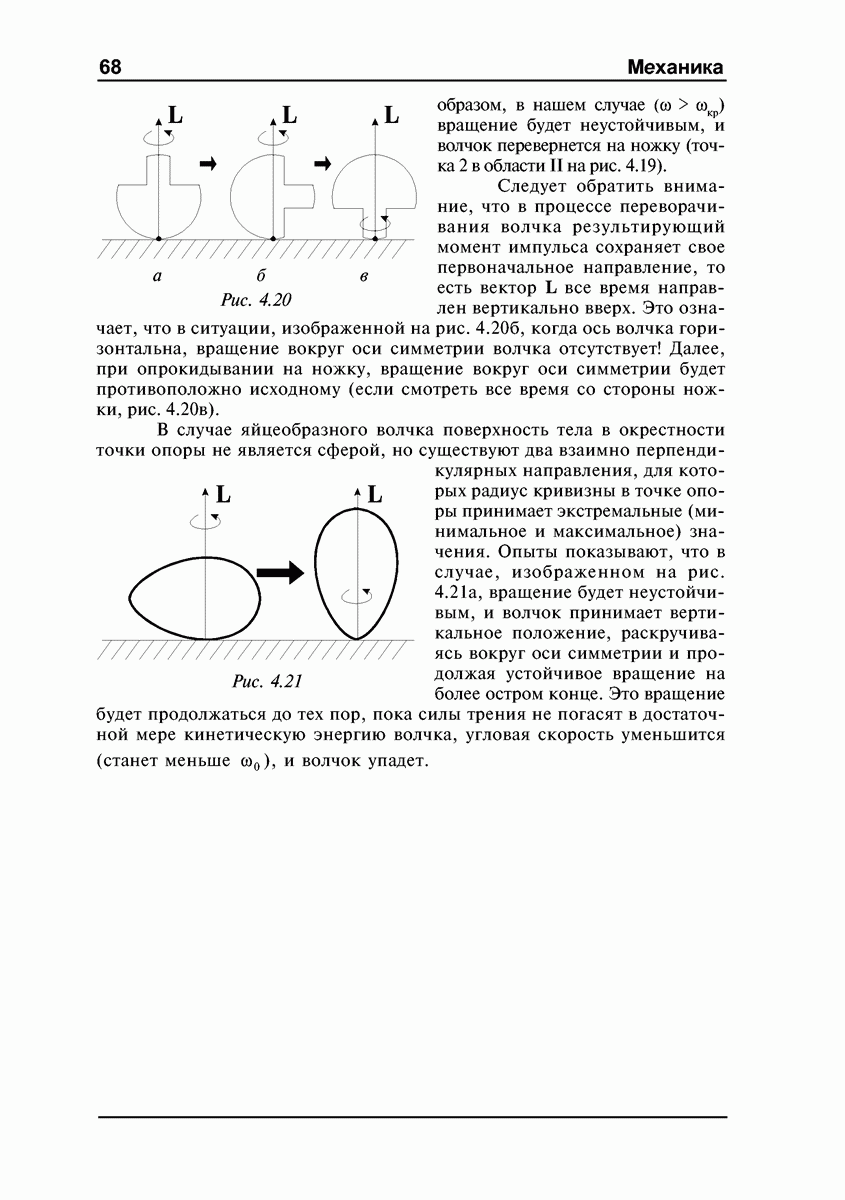
- Волчки.
- ЛИТЕРАТУРА