| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
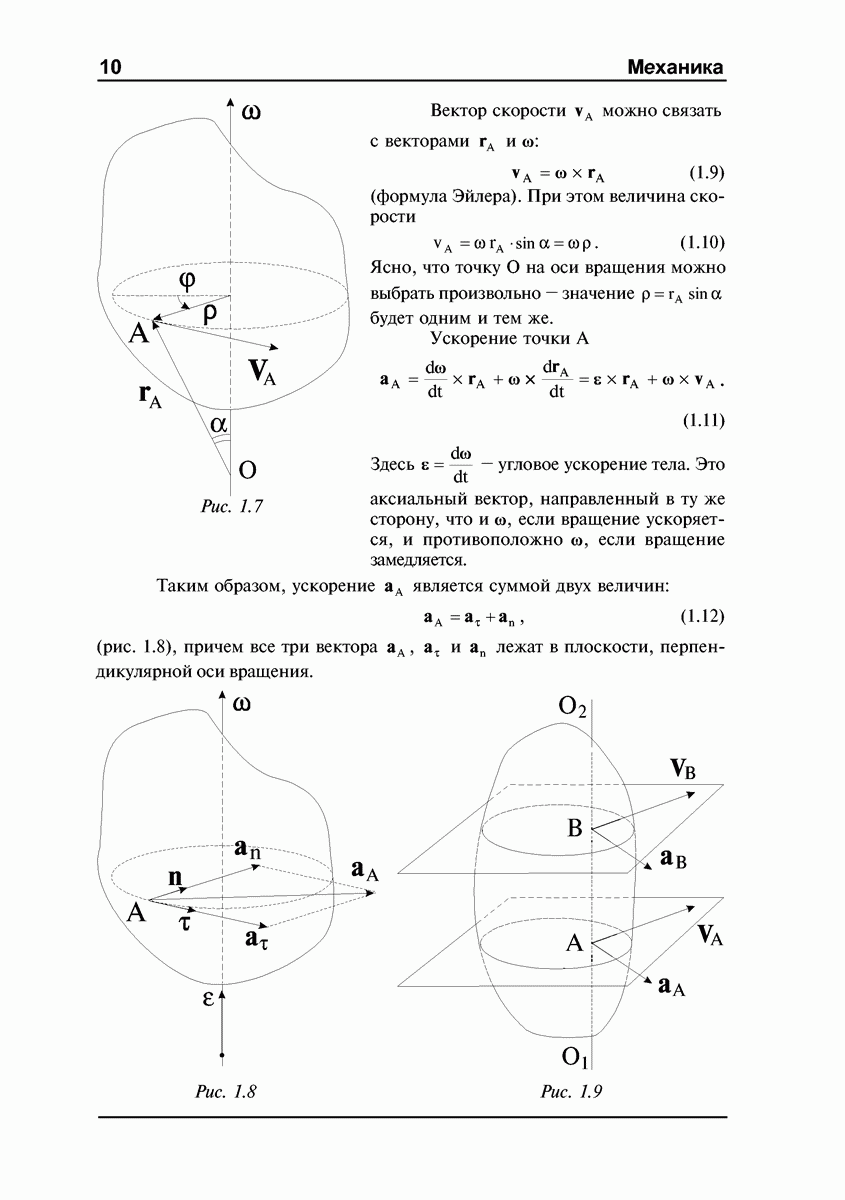
Уравнения Эйлера.
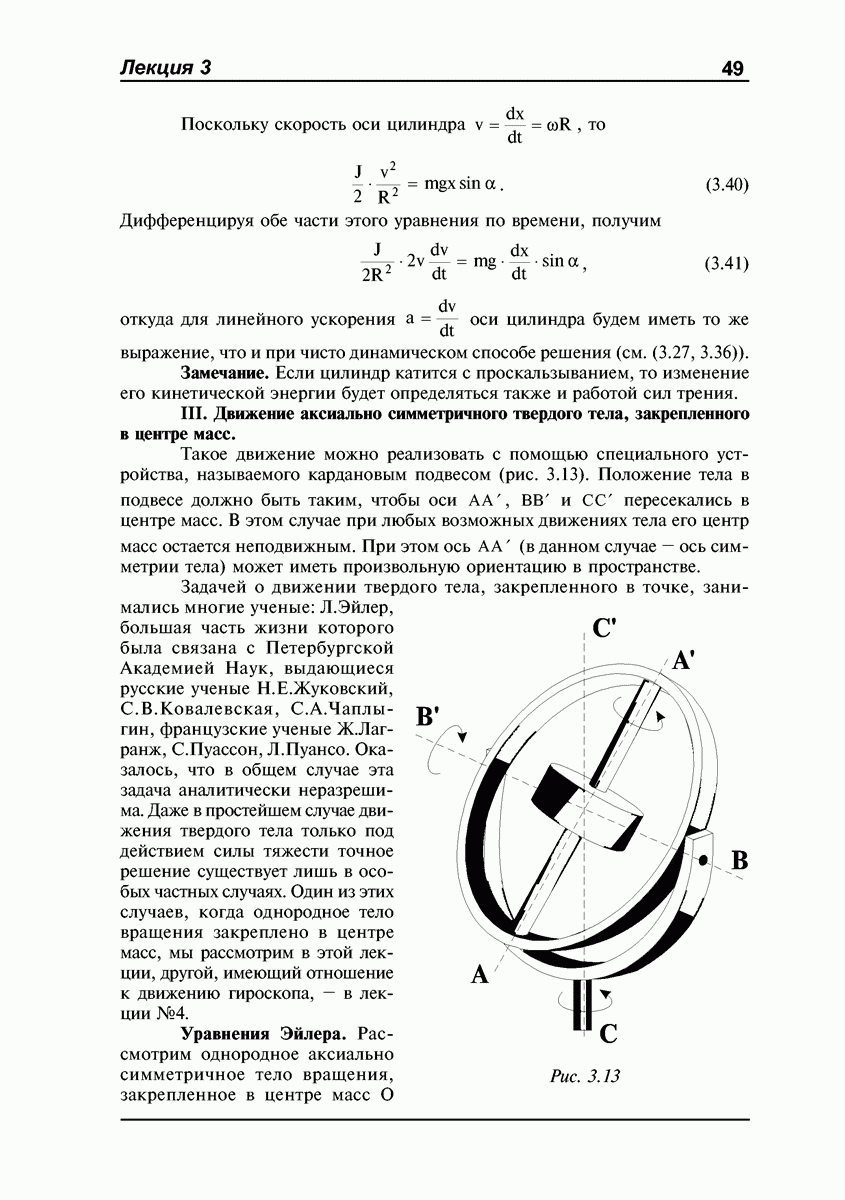
Рассмотрим однородное аксиально симметричное тело вращения, закрепленное в центре масс О

Рис. 3.13
(рис. 3.14). Центральный эллипсоид инерции такого тела является эллипсоидом вращения с осью симметрии 
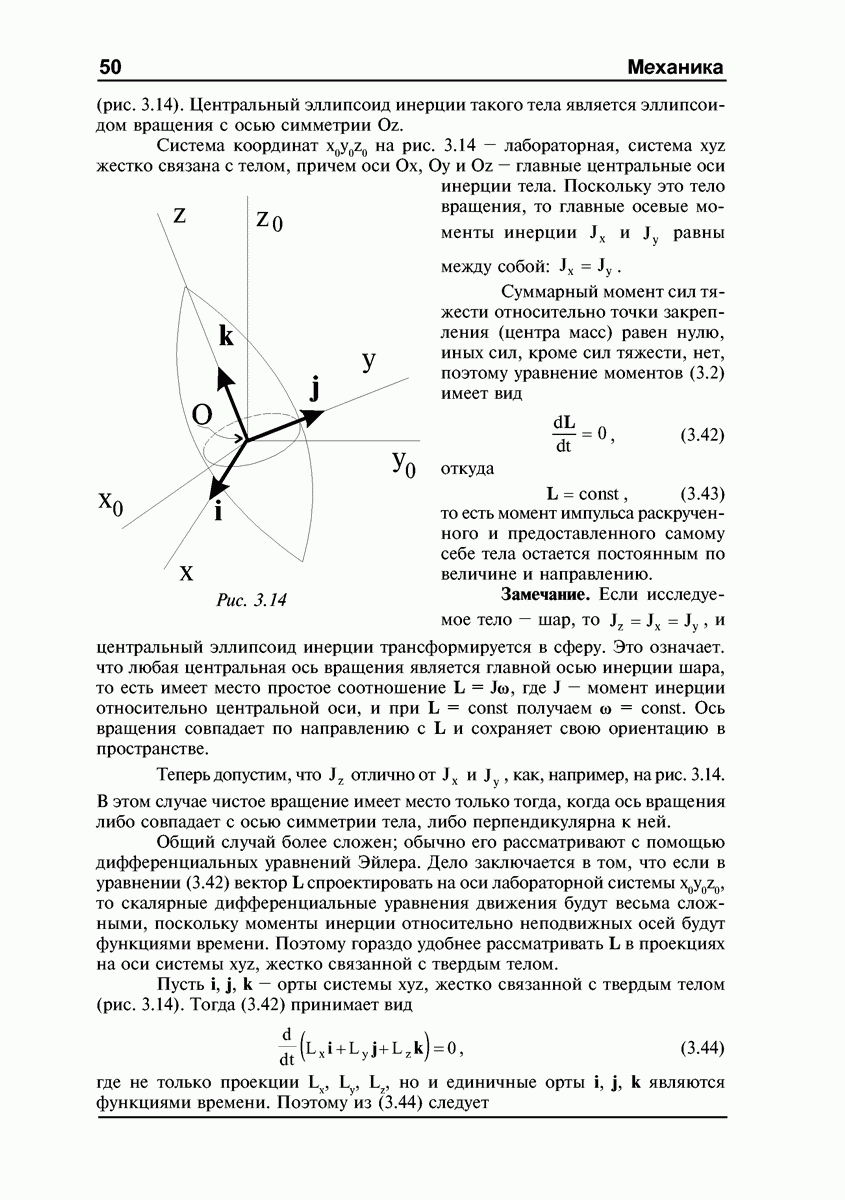
Система координат  на рис. 3.14 — лабораторная, система
на рис. 3.14 — лабораторная, система  жестко связана с телом, причем оси
жестко связана с телом, причем оси  — главные центральные оси инерции тела. Поскольку это тело вращения, то главные осевые моменты инерции
— главные центральные оси инерции тела. Поскольку это тело вращения, то главные осевые моменты инерции  равны между собой:
равны между собой:  .
.
Суммарный момент сил тяжести относительно точки закрепления (центра масс) равен нулю, иных сил, кроме сил тяжести, нет, поэтому уравнение моментов (3.2) имеет вид

откуда

то есть момент импульса раскрученного и предоставленного самому себе тела остается постоянным по величине и направлению.
Замечание. Если исследуемое тело — шар, то  и центральный эллипсоид инерции трансформируется в сферу. Это означает, что любая центральная ось вращения является главной осью инерции шара, то есть имеет место простое соотношение
и центральный эллипсоид инерции трансформируется в сферу. Это означает, что любая центральная ось вращения является главной осью инерции шара, то есть имеет место простое соотношение  где
где  — момент инерции относительно центральной оси, и при
— момент инерции относительно центральной оси, и при  получаем
получаем  Ось вращения совпадает по направлению с
Ось вращения совпадает по направлению с  и сохраняет свою ориентацию в пространстве.
и сохраняет свою ориентацию в пространстве.
Теперь допустим, что  отлично от
отлично от  как, например, на рис. 3.14.
как, например, на рис. 3.14.
В этом случае чистое вращение имеет место только тогда, когда ось вращения либо совпадает с осью симметрии тела, либо перпендикулярна к ней.
Общий случай более сложен; обычно его рассматривают с помощью дифференциальных уравнений Эйлера. Дело заключается в том, что если в уравнении (3.42) вектор  спроектировать на оси лабораторной системы
спроектировать на оси лабораторной системы  то скалярные дифференциальные уравнения движения будут весьма сложными, поскольку моменты инерции относительно неподвижных осей будут функциями времени. Поэтому гораздо удобнее рассматривать
то скалярные дифференциальные уравнения движения будут весьма сложными, поскольку моменты инерции относительно неподвижных осей будут функциями времени. Поэтому гораздо удобнее рассматривать  в проекциях на оси системы
в проекциях на оси системы  жестко связанной с твердым телом.
жестко связанной с твердым телом.
Пусть  — орты системы
— орты системы  жестко связанной с твердым телом (рис. 3.14). Тогда (3.42) принимает вид
жестко связанной с твердым телом (рис. 3.14). Тогда (3.42) принимает вид

где не только проекции  но и единичные орты
но и единичные орты  к являются функциями времени. Поэтому из (3.44) следует
к являются функциями времени. Поэтому из (3.44) следует

Рис. 3.14

Здесь использован символ  чтобы подчеркнуть, что рассматриваются изменения во времени проекций
чтобы подчеркнуть, что рассматриваются изменения во времени проекций  относительно подвижной системы
относительно подвижной системы  — системы, которая, в свою очередь, поворачивается вместе с телом с мгновенной угловой скоростью
— системы, которая, в свою очередь, поворачивается вместе с телом с мгновенной угловой скоростью 
Что касается производных по времени от единичных векторов  то их изменения во времени обусловлены только вращением системы
то их изменения во времени обусловлены только вращением системы  с угловой скоростью
с угловой скоростью  поэтому
поэтому

(см. рис. 3.15). Подставляя эти выражения в (3.45), получим:

Преобразование 

находится в полной аналогии с преобразованием скорости при переходе от неподвижной к вращающейся  системе координат. Существенно, что наблюдатель,
системе координат. Существенно, что наблюдатель,  находящийся в системе
находящийся в системе  фиксирует только относительное изменение
фиксирует только относительное изменение  (член
(член  ). Для наблюдателя в лабораторной системе к относительному изменению
). Для наблюдателя в лабораторной системе к относительному изменению  добавляется его “переносное” изменение, связанное с вращением системы
добавляется его “переносное” изменение, связанное с вращением системы  с мгновенной угловой скоростью
с мгновенной угловой скоростью 

Рис. 3.15
Проецируя векторы  на оси системы
на оси системы  жестко связанной с твердым телом, получим:
жестко связанной с твердым телом, получим:

Поскольку оси  — главные оси инерции для точки закрепления, то
— главные оси инерции для точки закрепления, то  и из
и из  будем иметь следующие уравнения:
будем иметь следующие уравнения:

где  — главные моменты инерции тела. Обычно эти уравнения называют уравнениями Эйлера при отсутствии моментов внешних сил.
— главные моменты инерции тела. Обычно эти уравнения называют уравнениями Эйлера при отсутствии моментов внешних сил.
В частном случае (рис. 3.14 )  и из (3.52-3.54) получаем:
и из (3.52-3.54) получаем:

где введено обозначение

Из (3.57) следует, что  то есть проекция вектора
то есть проекция вектора  на ось симметрии тела остается постоянной. Ясно, что
на ось симметрии тела остается постоянной. Ясно, что  — также постоянная величина. Ее физический смысл становится понятным, если записать решение уравнений (3.55, 3.56):
— также постоянная величина. Ее физический смысл становится понятным, если записать решение уравнений (3.55, 3.56):

где  — проекция вектора
— проекция вектора  на плоскость
на плоскость 
Таким образом, вектор  составляет с осью симметрии тела угол
составляет с осью симметрии тела угол  и вращается вокруг этой оси, как следует из (3.59), с постоянной угловой скоростью
и вращается вокруг этой оси, как следует из (3.59), с постоянной угловой скоростью  . Начальная фаза
. Начальная фаза  этого вращения определяется начальными условиями.
этого вращения определяется начальными условиями.
Посмотрим, как будет выглядеть движение твердого тела в лабораторной системе  Поскольку нам известны значения
Поскольку нам известны значения  то закон движения тела (зависимость углов Эйлера от времени) в принципе может быть получен из кинематических уравнений Эйлера (1.30 - 1.32). Однако это связано с решением в общем случае довольно сложных дифференциальных уравнений, поэтому мы ограничимся качественным рассмотрением движения тела. В силу того, что
то закон движения тела (зависимость углов Эйлера от времени) в принципе может быть получен из кинематических уравнений Эйлера (1.30 - 1.32). Однако это связано с решением в общем случае довольно сложных дифференциальных уравнений, поэтому мы ограничимся качественным рассмотрением движения тела. В силу того, что

( — орты главных осей инерции тела),
— орты главных осей инерции тела),  можно записать
можно записать

Здесь добавлен и вычтен член  что позволяет представить (3.61) в виде
что позволяет представить (3.61) в виде

Отсюда видно, что к (ось фигуры),  и
и  лежат в одной плоскости. Из (3.62) следует, что
лежат в одной плоскости. Из (3.62) следует, что

где

есть составляющая угловой скорости по направлению  Плоскость, в которой лежат ось фигуры,
Плоскость, в которой лежат ось фигуры,  и
и  поворачивается (прецессирует) вокруг направления
поворачивается (прецессирует) вокруг направления  с угловой скоростью
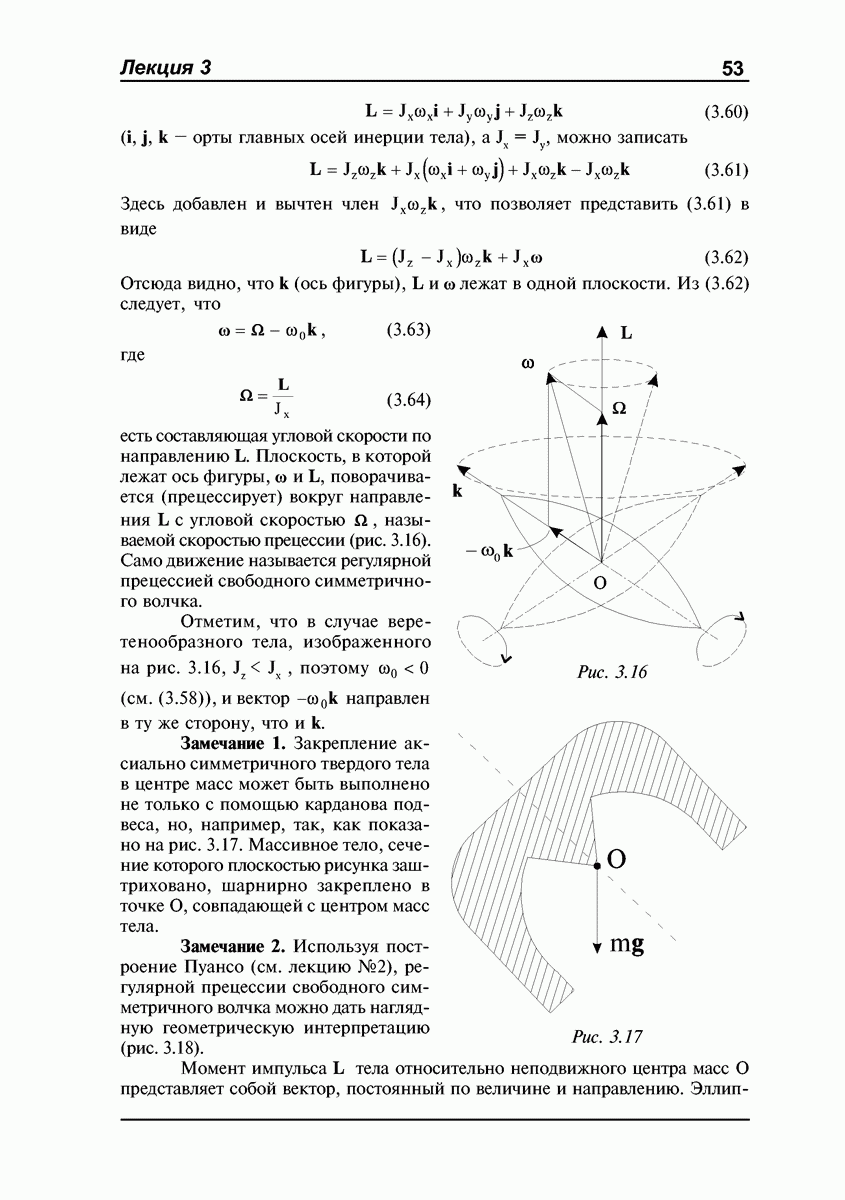
с угловой скоростью  называемой скоростью прецессии (рис. 3.16).
называемой скоростью прецессии (рис. 3.16).
Само движение называется регулярной прецессией свободного симметричного волчка.
Отметим, что в случае веретенообразного тела, изображенного на рис. 3.16,  , поэтому
, поэтому  (см. (3.58)), и вектор
(см. (3.58)), и вектор  направлен в ту же сторону, что и k.
направлен в ту же сторону, что и k.
Замечание 1. Закрепление аксиально симметричного твердого тела в центре масс может быть выполнено не только с помощью карданова подвеса, но, например, так, как показано на рис. 3.17. Массивное тело, сечение которого плоскостью рисунка заштриховано, шарнирно закреплено в точке О, совпадающей с центром масс тела.
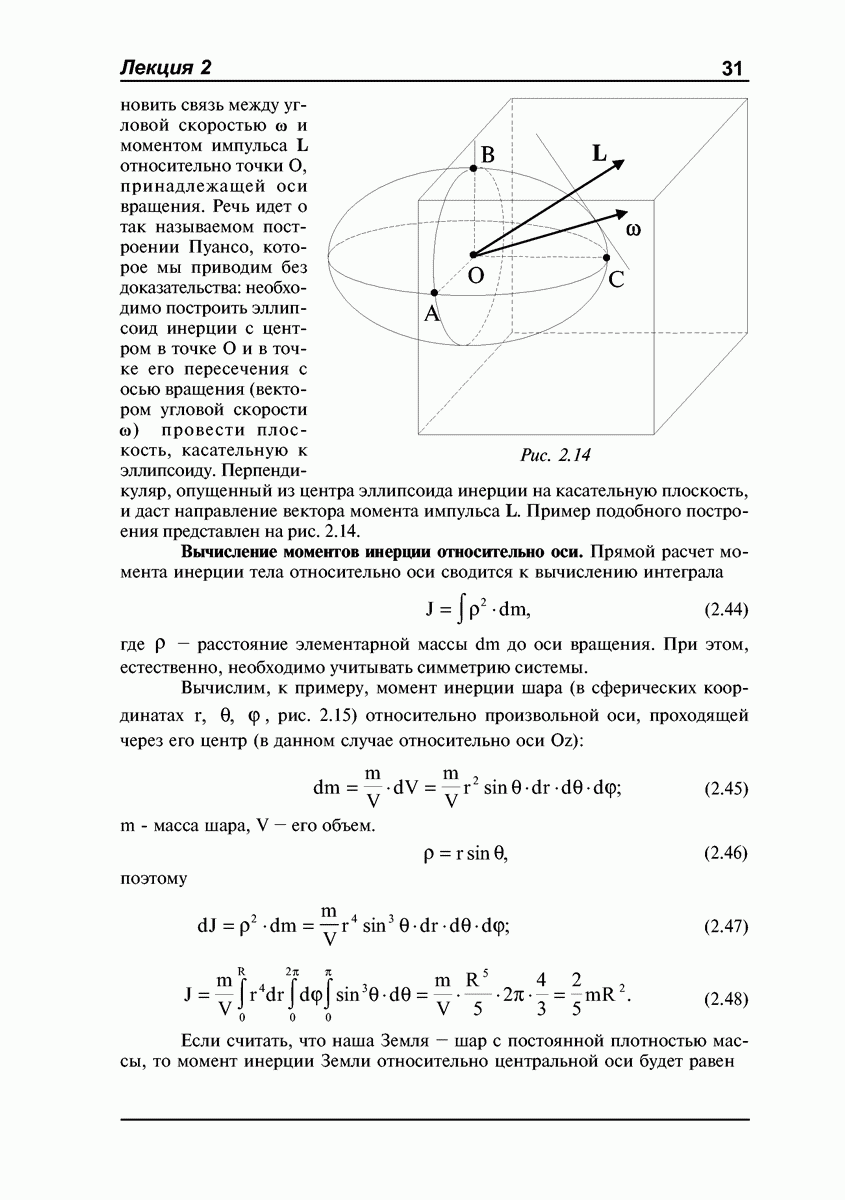
Замечание 2. Используя построение Пуансо (см. лекцию №2), регулярной прецессии свободного симметричного волчка можно дать наглядную геометрическую интерпретацию (рис. 3.18).
Момент импульса  тела относительно неподвижного центра масс О представляет собой вектор, постоянный по величине и направлению.
тела относительно неподвижного центра масс О представляет собой вектор, постоянный по величине и направлению.

Рис. 3.16

Рис. 3.17

Рис. 3.18
Эллипсоид инерции тела с центром в точке О, сечение которого изображено на рис. 3.18, является эллипсоидом вращения. Касательная к эллипсоиду плоскость  проведена через полюс Р пересечения мгновенной угловой скорости со с эллипсоидом; эта плоскость перпендикулярна к вектору
проведена через полюс Р пересечения мгновенной угловой скорости со с эллипсоидом; эта плоскость перпендикулярна к вектору  и в лабораторной системе отсчета сохраняет свое положение неизменным. При регулярной прецессии волчка эллипсоид инерции тела катится по плоскости
и в лабораторной системе отсчета сохраняет свое положение неизменным. При регулярной прецессии волчка эллипсоид инерции тела катится по плоскости  без скольжения, так что геометрическим местом полюсов Р является окружность радиуса
без скольжения, так что геометрическим местом полюсов Р является окружность радиуса  принадлежащая плоскости
принадлежащая плоскости 
Замечание 3. Во избежание путаницы отметим следующее. Описанное выше движение связано с изменением угла прецессии V (см. рис. 1.3), поэтому оно и было названо регулярной прецессией (кинематическое определение). Однако существуют определения прецессии как движения оси симметрии тела под действием момента внешних сил (динамическое определение, см. лекцию №4). Описанное же выше движение с точки зрения динамического определения называют нутацией.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- ЛЕКЦИЯ №1. Кинематика абсолютно твердого тела. Степени свободы. Углы Эйлера. Поступательное движение. Вращение вокруг неподвижной оси. Плоское движение. Движение твердого тела, имеющего одну неподвижную точку. Движение свободного твердого тела.
- Поступательное движение
- Вращение вокруг неподвижной оси
- Плоское движение
- Движение твердого тела с одной неподвижной точкой.
- Движение свободного твердого тела.
- ЛЕКЦИЯ №2. Динамика абсолютно твердого тела. Момент импульса. Тензор инерции. Момент импульса тела относительно оси. Эллипсоид инерции. Вычисление моментов инерции относительно оси. Теорема Гюйгенса-Штейнера. Момент импульса относительно движущегося центра масс.
- Главные оси инерции.
- Момент импульса твердого тела относительно оси. Момент инерции относительно оси.
- Эллипсоид инерции.
- Вычисление моментов инерции относительно оси.
- Теорема Гюйгенса-Штейнера.
- Момент импульса тела относительно движущегося центра масс.
- ЛЕКЦИЯ №3. Динамика абсолютно твердого тела. Уравнение поступательного движения и уравнение моментов. Вращение твердого тела вокруг неподвижной оси. Центр удара. Динамика плоского движения твердого тела. Движение аксиально симметричного твердого тела, закрепленного в центре масс. Уравнения Эйлера.
- Уравнения динамики твердого тела. Общий случай.
- Кинетическая энергия вращающегося тела и работа внешних сил (ось вращения неподвижна).
- Свободные оси. Устойчивость свободного вращения.
- Центр удара.
- Кинетическая энергия при плоском движении.
- Уравнения Эйлера.
- ЛЕКЦИЯ №4. Гироскопы. Свободный гироскоп. Прецессия гироскопа под действием внешних сил. Угловая скорость прецессии. Нутации. Гироскопические силы, их природа и проявления.
- Свободный гироскоп.
- Прецессия гироскопа под действием внешних сил. Элементарная теория.
- Прецессия гироскопа под действием внешних сил. Отход от элементарной теории. Нутации.
- Гироскопические силы.
- Волчки.
- ЛИТЕРАТУРА