| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
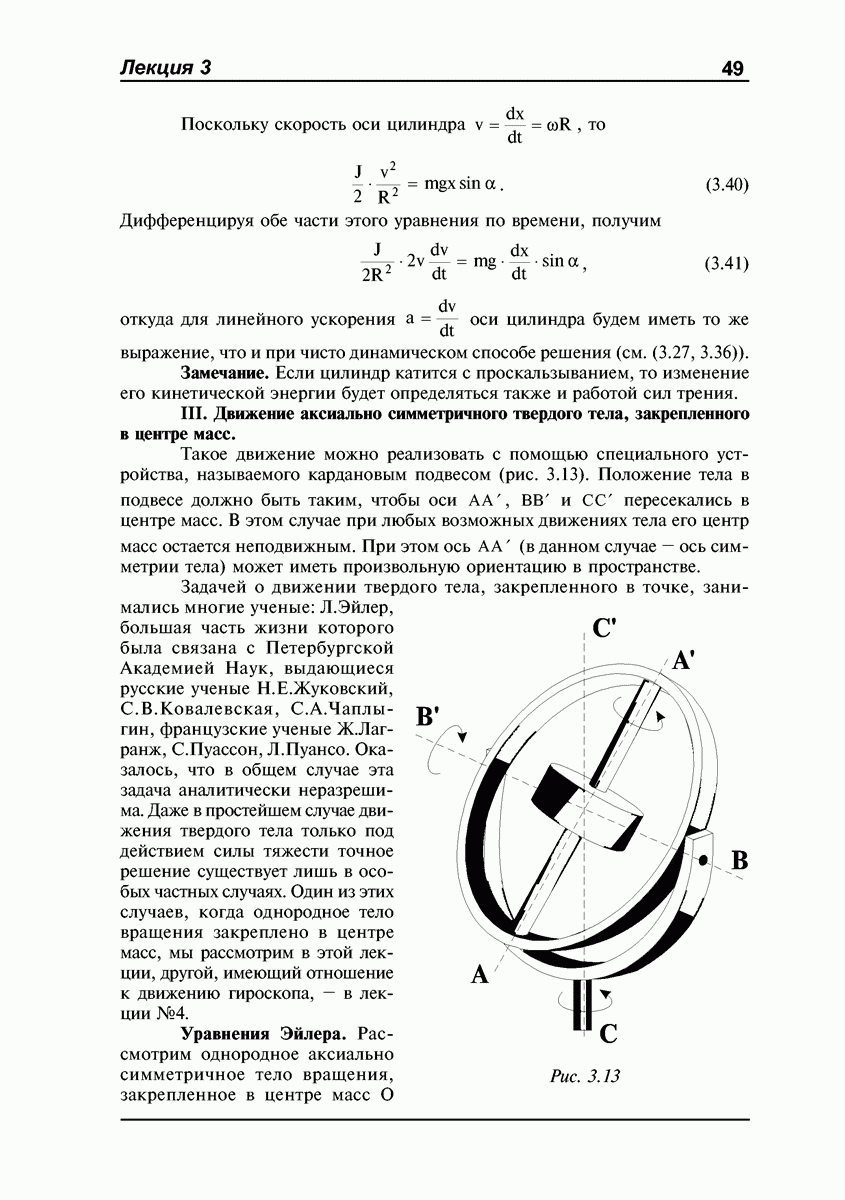
Вращение вокруг неподвижной оси
Если при движении твердого тела какие-либо две его точки все время остаются неподвижными, то через эти точки можно провести прямую, являющуюся неподвижной осью вращения. С таким движением мы сталкиваемся ежедневно, открывая и закрывая дверь в комнату. Очевидно, что в этом случае тело обладает лишь одной степенью свободы, связанной с углом его поворота вокруг оси. При этом все точки тела движутся по окружностям, лежащим в плоскостях, которые перпендикулярны оси вращения; центры окружностей лежат на этой оси.
Существенно, что линейные скорости точек, находящихся на разном расстоянии от оси вращения, разные. В этом можно убедиться, касаясь стальной проволокой вращающегося диска точила (рис. 1.6): чем дальше от оси, тем длиннее сноп искр — тем больше скорость соответствующей точки диска.

Рис. 1.6
При этом также видно, что искры летят по касательной к окружности, описываемой данной точкой диска.
Ясно, что угловое перемещение всех точек твердого тела за одно и то же время будет одинаковым. Это обстоятельство позволяет ввести общую кинематическую характеристику — угловую скорость

 — угол поворота тела за время
— угол поворота тела за время 
Можно ввести вектор элементарного углового перемещения  направленный вдоль оси вращения в соответствии с правилом правого буравчика: если рукоятку буравчика поворачивать в направлении вращения тела, то поступательное перемещение буравчика даст направление
направленный вдоль оси вращения в соответствии с правилом правого буравчика: если рукоятку буравчика поворачивать в направлении вращения тела, то поступательное перемещение буравчика даст направление  Устремляя интервал времени
Устремляя интервал времени  за которое произошло угловое перемещение
за которое произошло угловое перемещение  к нулю, мы получим вектор угловой скорости
к нулю, мы получим вектор угловой скорости

который определяет, во-первых, модуль угловой скорости тела, во-вторых,
— ориентацию оси вращения в пространстве, и в-третьих, — направление вращения тела. Следует подчеркнуть, что  — вектор скользящий в том смысле, что его начало можно совместить с любой точкой, принадлежащей оси вращения.
— вектор скользящий в том смысле, что его начало можно совместить с любой точкой, принадлежащей оси вращения.
Например, для Земли, вращающейся вокруг своей оси с запада на восток, вектор  имеет направление от южного полюса к северному. Величина угловой скорости
имеет направление от южного полюса к северному. Величина угловой скорости

Для сравнения: угловая скорость орбитального движения Земли составляет

Заметим, что период орбитального движения не кратен продолжительности суток, что создает известные трудности в построении календаря (необходимо вводить високосные годы и проч.).
Зная  , легко определить линейную скорость любой точки твердого тела. Введем радиус-вектор
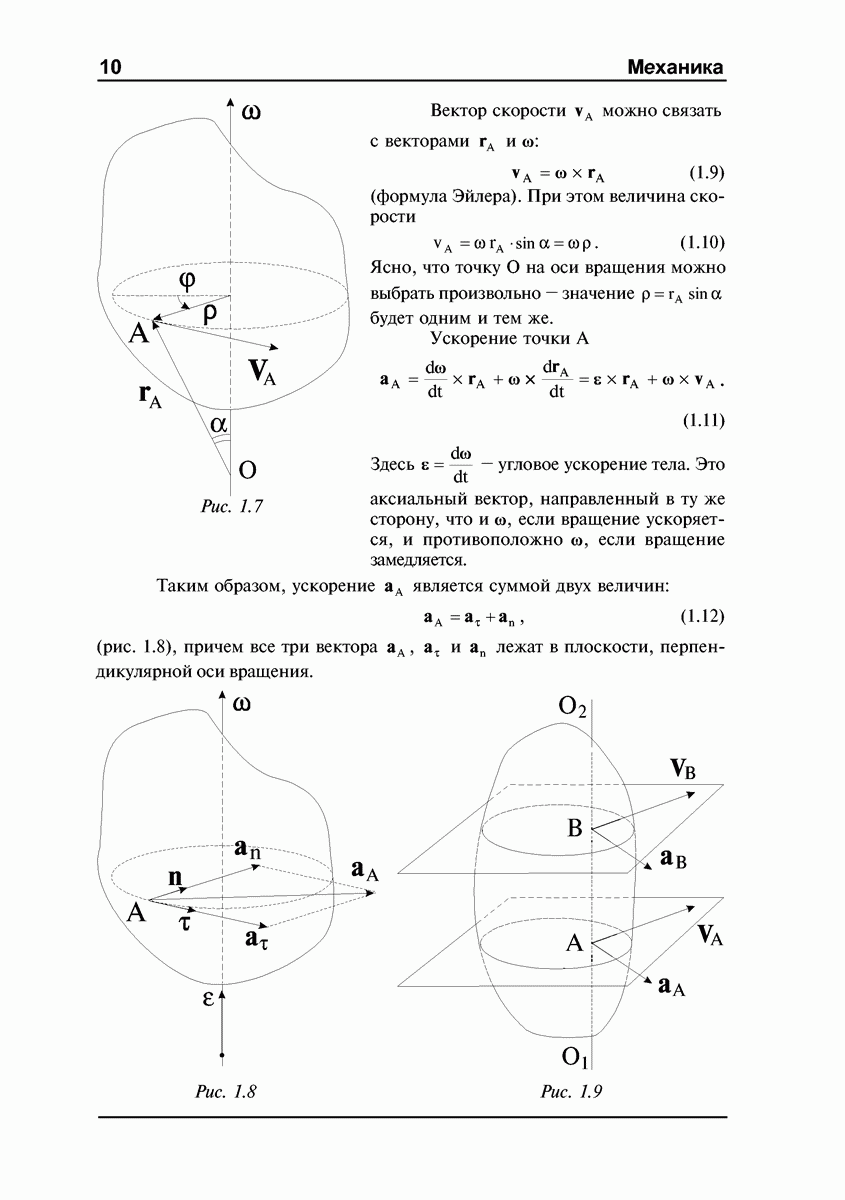
, легко определить линейную скорость любой точки твердого тела. Введем радиус-вектор  некоторой точки А твердого тела, поместив его начало в точку О на оси вращения (рис. 1.7). Вектор
некоторой точки А твердого тела, поместив его начало в точку О на оси вращения (рис. 1.7). Вектор  проведен в точку А от оси вращения, то есть перпендикулярно оси.
проведен в точку А от оси вращения, то есть перпендикулярно оси.

Рис. 1.7
Вектор скорости  можно связать с векторами
можно связать с векторами 

(формула Эйлера). При этом величина скорости

Ясно, что точку О на оси вращения можно выбрать произвольно — значение  будет одним и тем же.
будет одним и тем же.
Ускорение точки А

Здесь  угловое ускорение тела. Это аксиальный вектор, направленный в ту же сторону, что и
угловое ускорение тела. Это аксиальный вектор, направленный в ту же сторону, что и  , если вращение ускоряется, и противоположно
, если вращение ускоряется, и противоположно  , если вращение замедляется.
, если вращение замедляется.
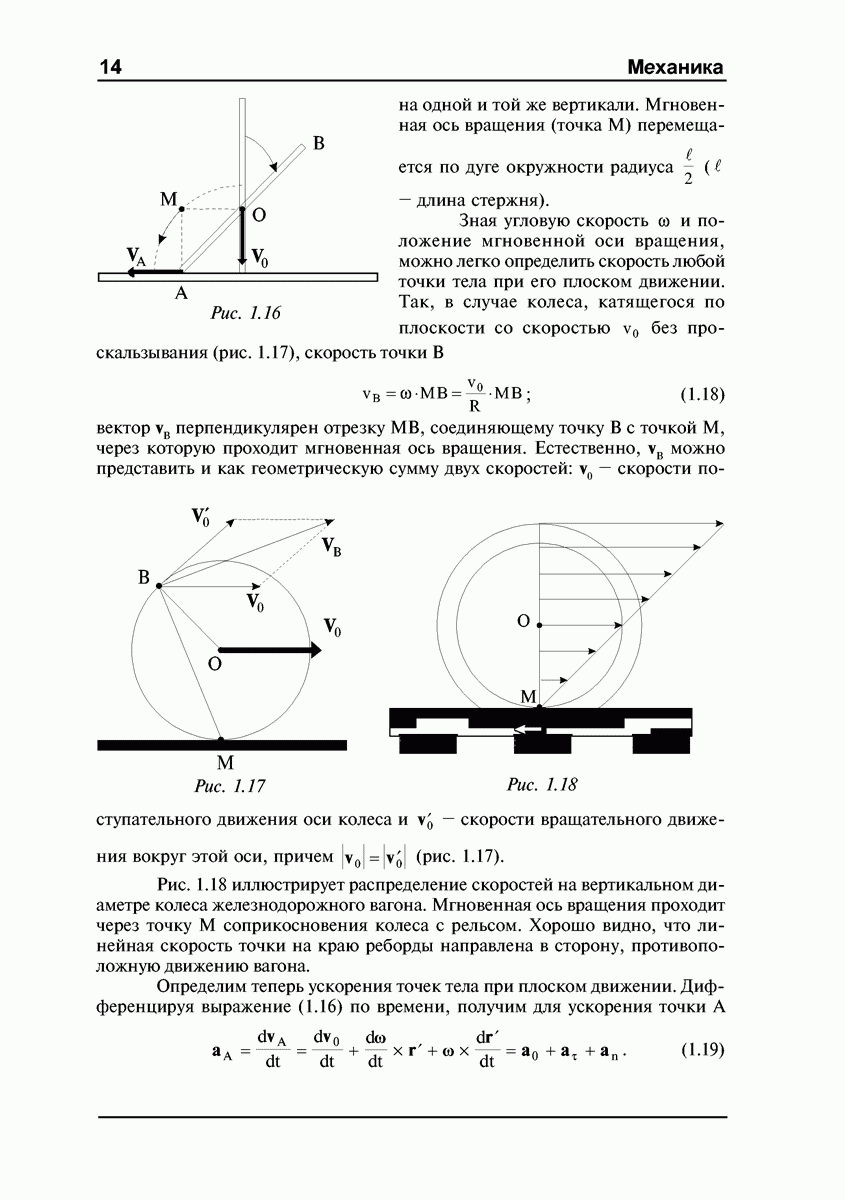
Таким образом, ускорение  является суммой двух величин:
является суммой двух величин:

(рис. 1.8), причем все три вектора  лежат в плоскости, перпендикулярной оси вращения.
лежат в плоскости, перпендикулярной оси вращения.

Рис. 1.8

Рис. 1.9

— это тангенциальное ускорение  — единичный вектор в направлении
— единичный вектор в направлении 

— это центростремительное ускорение  — единичный вектор в направлении к оси вращения). Эти составляющие полного ускорения хорошо известны из кинематики вращательного движения материальной точки.
— единичный вектор в направлении к оси вращения). Эти составляющие полного ускорения хорошо известны из кинематики вращательного движения материальной точки.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- ЛЕКЦИЯ №1. Кинематика абсолютно твердого тела. Степени свободы. Углы Эйлера. Поступательное движение. Вращение вокруг неподвижной оси. Плоское движение. Движение твердого тела, имеющего одну неподвижную точку. Движение свободного твердого тела.
- Поступательное движение
- Вращение вокруг неподвижной оси
- Плоское движение
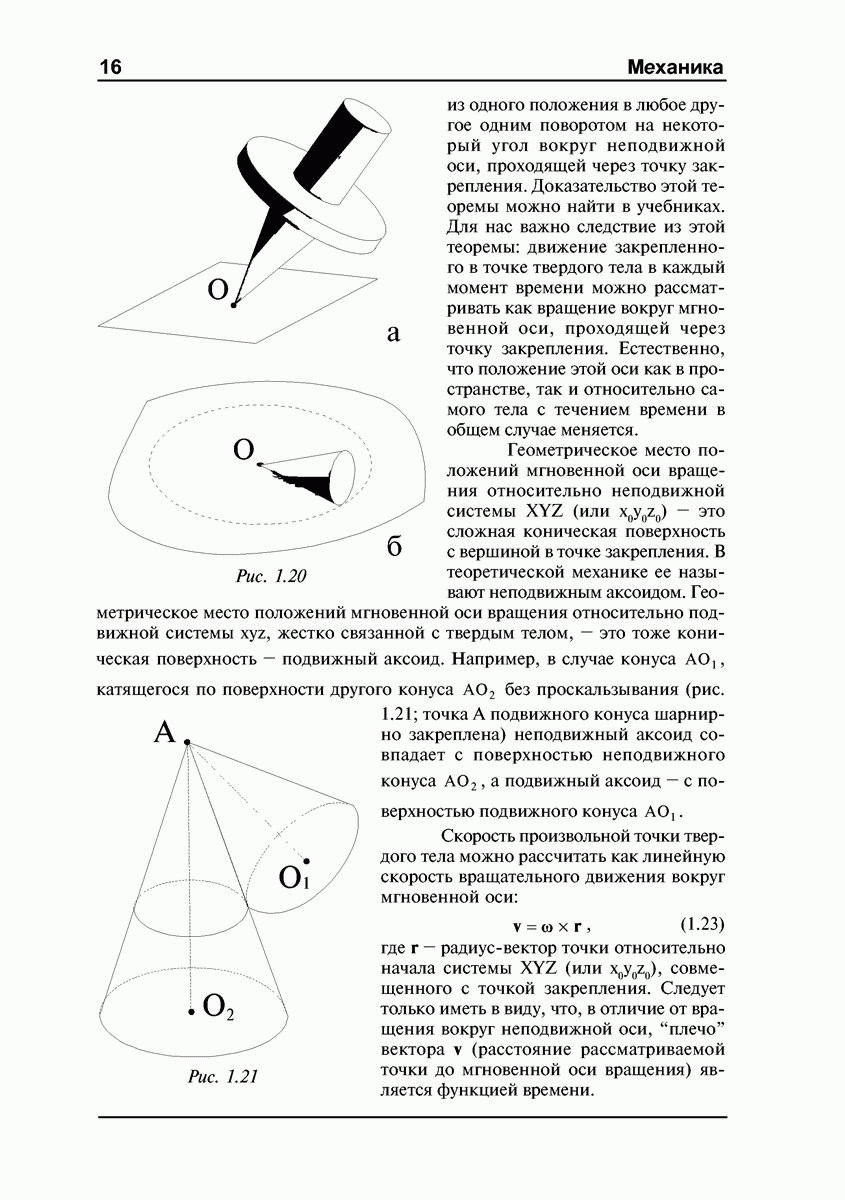
- Движение твердого тела с одной неподвижной точкой.
- Движение свободного твердого тела.
- ЛЕКЦИЯ №2. Динамика абсолютно твердого тела. Момент импульса. Тензор инерции. Момент импульса тела относительно оси. Эллипсоид инерции. Вычисление моментов инерции относительно оси. Теорема Гюйгенса-Штейнера. Момент импульса относительно движущегося центра масс.
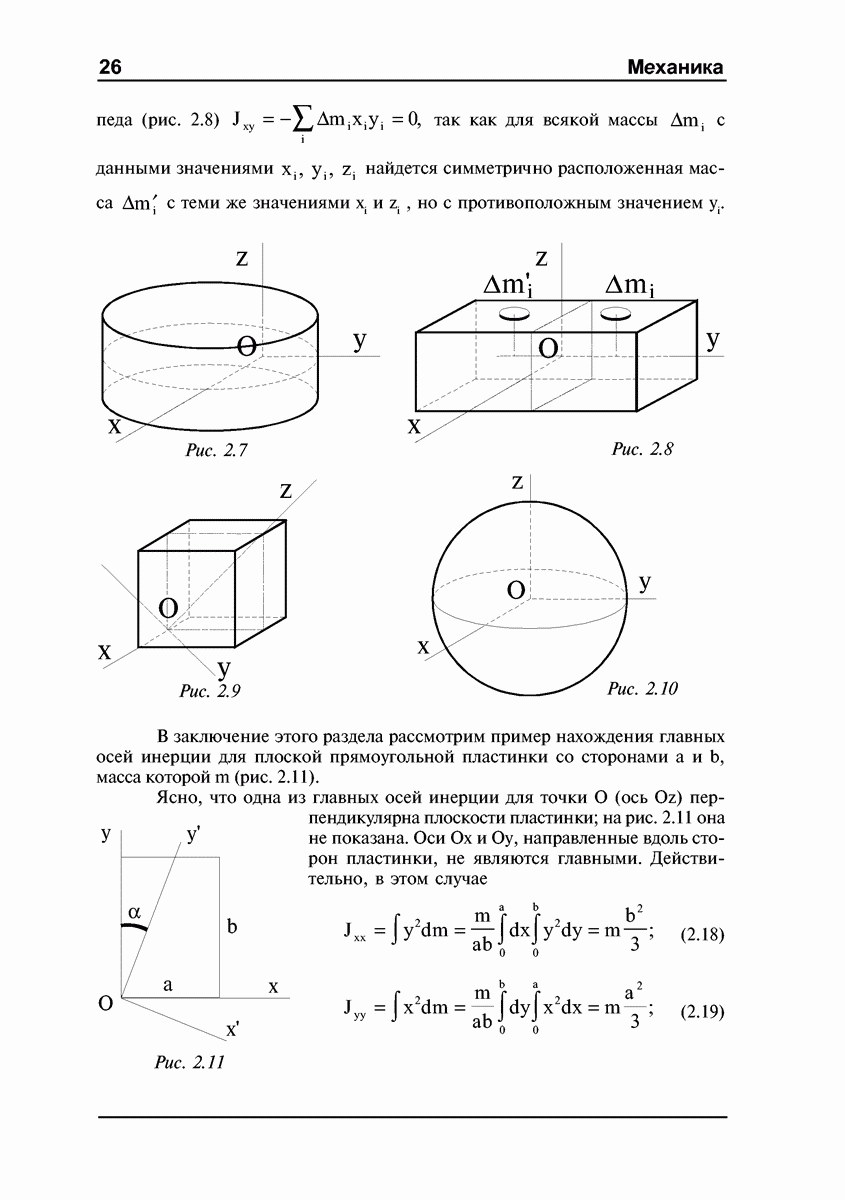
- Главные оси инерции.
- Момент импульса твердого тела относительно оси. Момент инерции относительно оси.
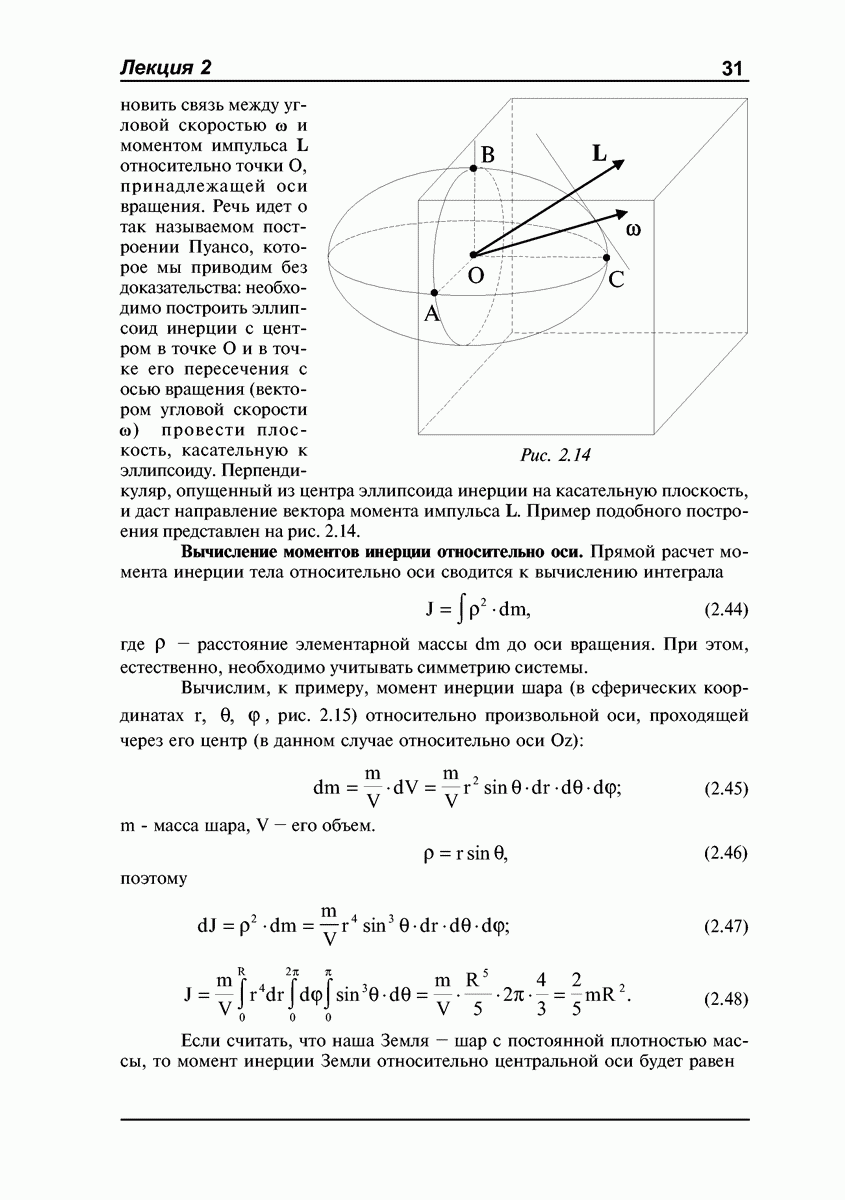
- Эллипсоид инерции.
- Вычисление моментов инерции относительно оси.
- Теорема Гюйгенса-Штейнера.
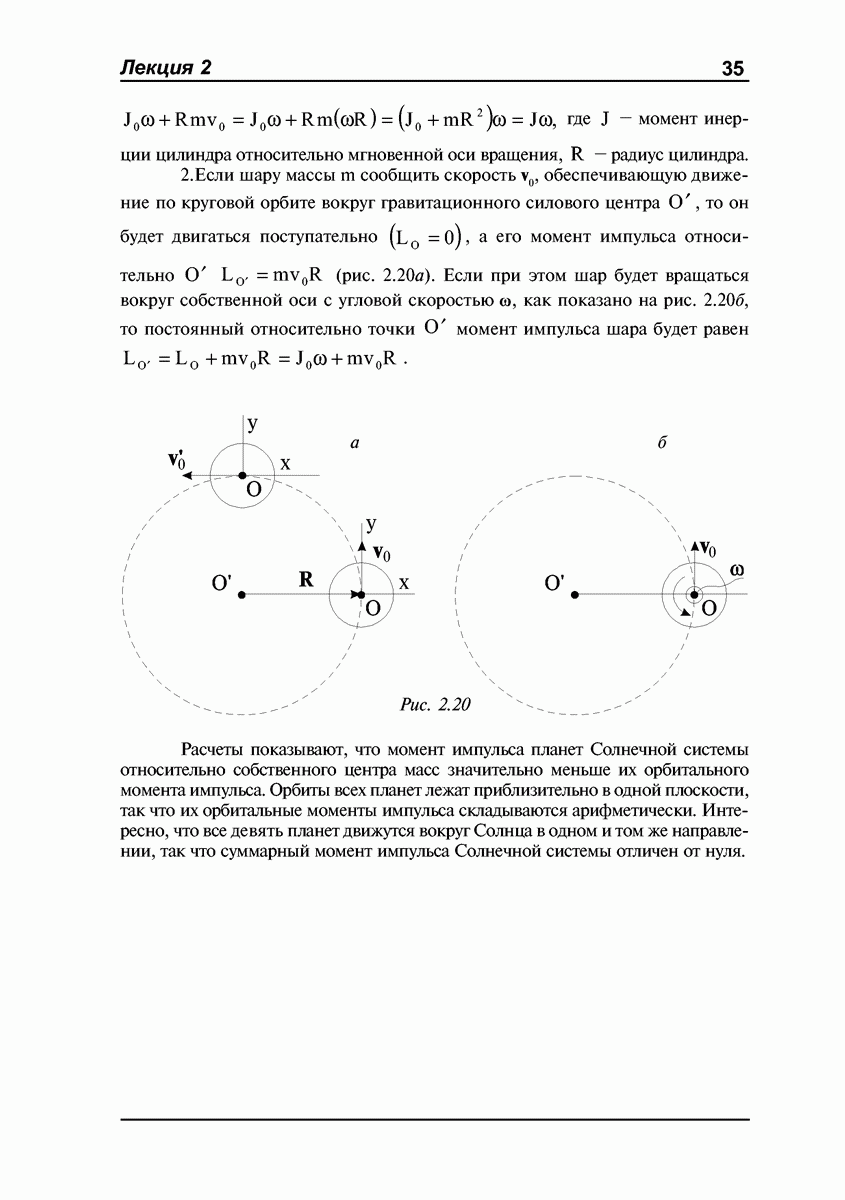
- Момент импульса тела относительно движущегося центра масс.
- ЛЕКЦИЯ №3. Динамика абсолютно твердого тела. Уравнение поступательного движения и уравнение моментов. Вращение твердого тела вокруг неподвижной оси. Центр удара. Динамика плоского движения твердого тела. Движение аксиально симметричного твердого тела, закрепленного в центре масс. Уравнения Эйлера.
- Уравнения динамики твердого тела. Общий случай.
- Кинетическая энергия вращающегося тела и работа внешних сил (ось вращения неподвижна).
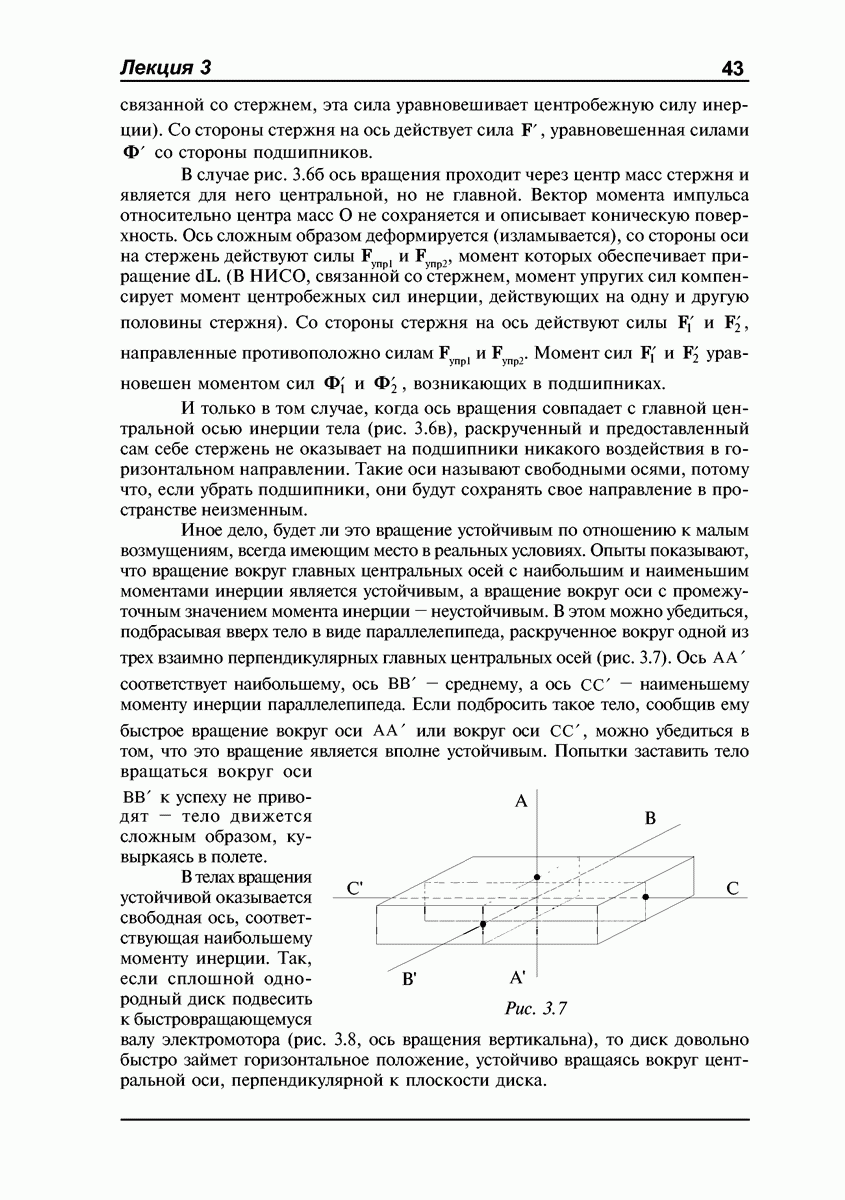
- Свободные оси. Устойчивость свободного вращения.
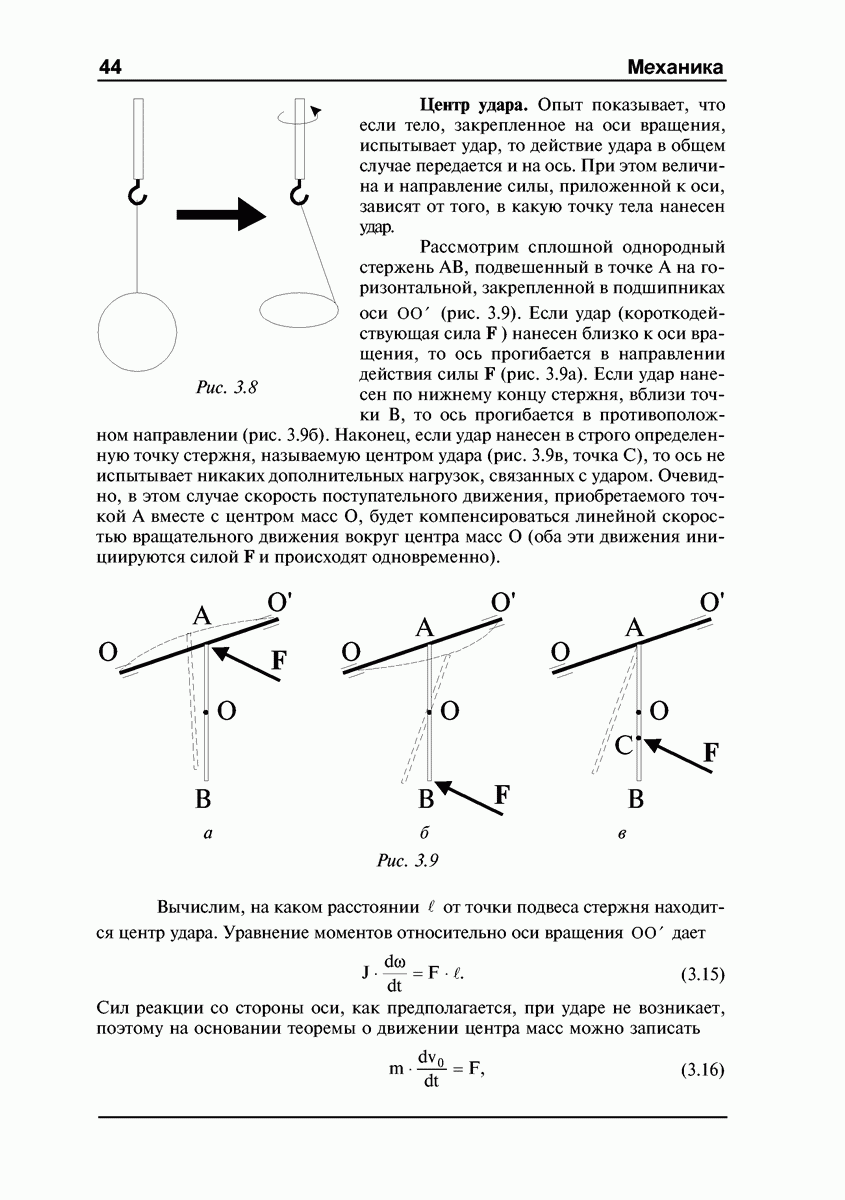
- Центр удара.
- Кинетическая энергия при плоском движении.
- Уравнения Эйлера.
- ЛЕКЦИЯ №4. Гироскопы. Свободный гироскоп. Прецессия гироскопа под действием внешних сил. Угловая скорость прецессии. Нутации. Гироскопические силы, их природа и проявления.
- Свободный гироскоп.
- Прецессия гироскопа под действием внешних сил. Элементарная теория.
- Прецессия гироскопа под действием внешних сил. Отход от элементарной теории. Нутации.
- Гироскопические силы.
- Волчки.
- ЛИТЕРАТУРА