| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Волчки.
Волчки кардинально отличаются от гироскопов тем, что в общем случае они не имеют ни одной неподвижной точки. Произвольное движение волчков имеет весьма сложный характер: будучи раскручены вокруг оси симметрии и поставлены на плоскость, они прецессируют,  по плоскости, выписывая замысловатые фигуры, а иногда даже переворачиваются с одного конца на другой. Не вдаваясь в детали такого необычного поведения волчков, отметим лишь, что немаловажную роль здесь играет сила трения, возникающая в точке соприкосновения волчка и плоскости.
по плоскости, выписывая замысловатые фигуры, а иногда даже переворачиваются с одного конца на другой. Не вдаваясь в детали такого необычного поведения волчков, отметим лишь, что немаловажную роль здесь играет сила трения, возникающая в точке соприкосновения волчка и плоскости.
Кратко остановимся на вопросе об устойчивости вращения симметричного волчка произвольной формы. Опыт показывает, что если симметричный волчок привести во вращение вокруг оси симметрии и установить на плоскость в вертикальном положении, то это вращение в зависимости от

Рис. 4.18
формы волчка и угловой скорости вращения будет либо устойчивым, либо неустойчивым.
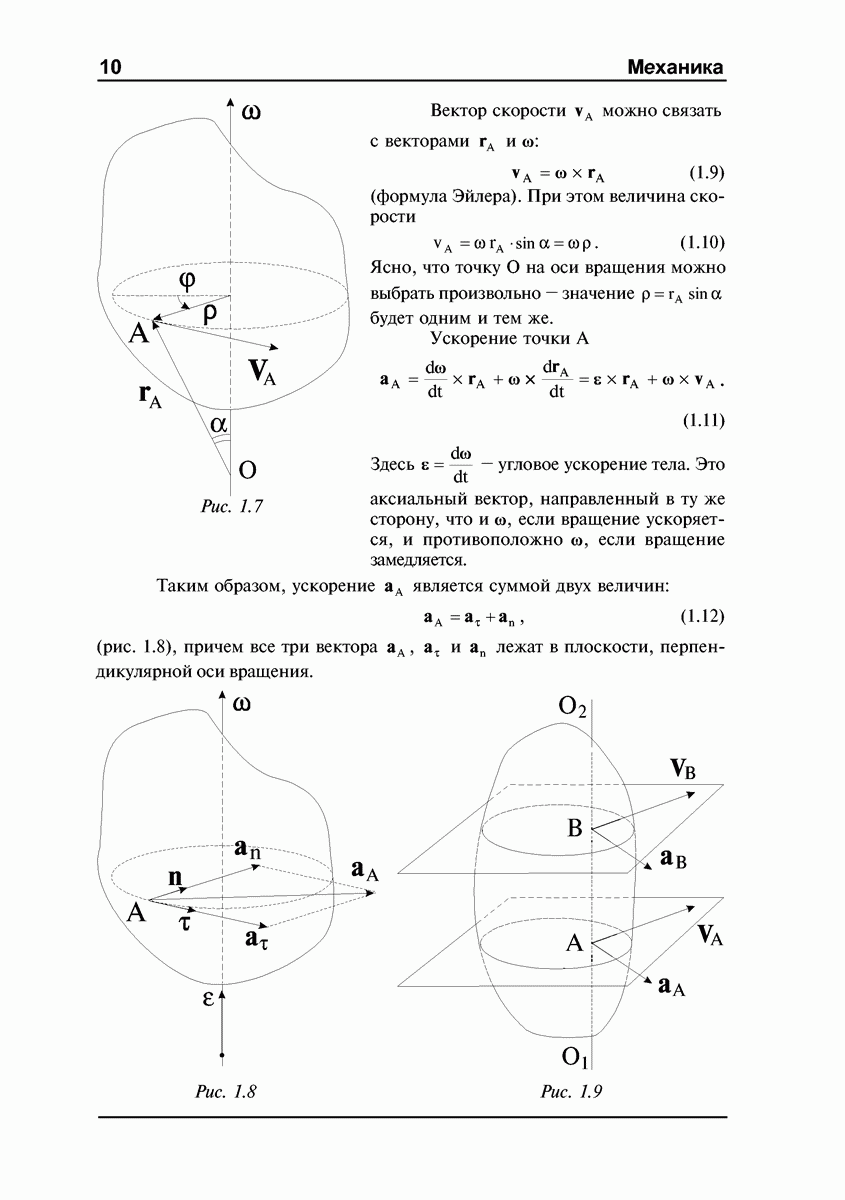
Пусть имеется симметричный волчок, изображенный на рис. 4.18. Введем следующие обозначения: О — центр масс волчка,  — расстояние от центра масс до точки опоры; К — центр кривизны волчка в точке опоры,
— расстояние от центра масс до точки опоры; К — центр кривизны волчка в точке опоры,  — радиус кривизны;
— радиус кривизны;  — момент инерции относительно оси симметрии,
— момент инерции относительно оси симметрии,  — момент инерции относительно главной центральной оси, перпендикулярной оси симметрии.
— момент инерции относительно главной центральной оси, перпендикулярной оси симметрии.
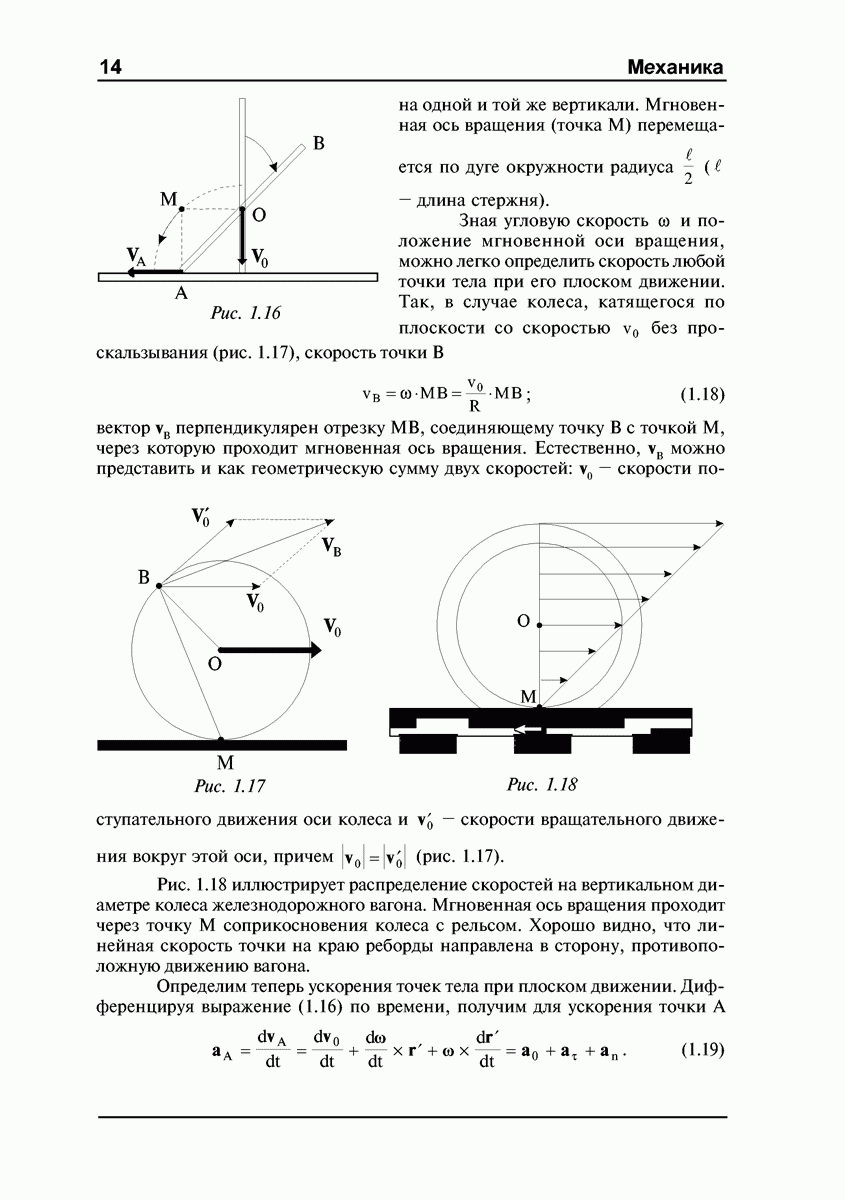
Анализ устойчивости вращения волчка приводит к диаграмме, изображенной на рис. 4.19 [8]. Здесь по оси абсцисс отложено отношение —  а по оси ординат — отношение
а по оси ординат — отношение 
Проведем гиперболу  и прямую
и прямую  Эти линии делят область положительных значении
Эти линии делят область положительных значении  на 4 части.
на 4 части.
Область I соответствует неустойчивому вращению волчка при всех угловых скоростях, область II — устойчивому вращению при достаточно больших угловых скоростях  Область III соответствует устойчивому вращению при малых угловых скоростях
Область III соответствует устойчивому вращению при малых угловых скоростях  область IV — устойчивому вращению при произвольных
область IV — устойчивому вращению при произвольных  Критическая угловая скорость
Критическая угловая скорость  зависит от моментов инерции
зависит от моментов инерции  расстояний
расстояний  и веса тела
и веса тела 

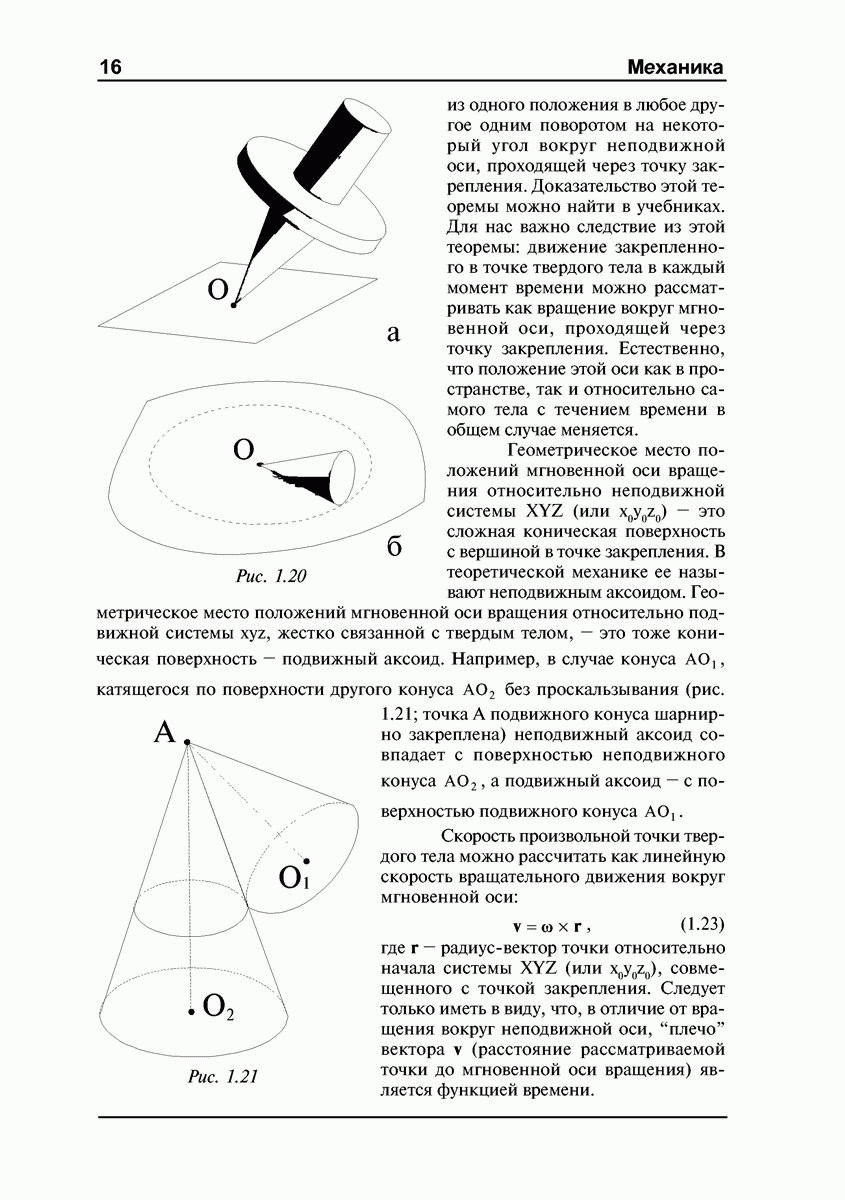
Рассмотрим, например, китайский волчок, раскрученный до  и поставленный на плоскость вертикально, как показано на рис. 4.20 а. Пусть
и поставленный на плоскость вертикально, как показано на рис. 4.20 а. Пусть  Поскольку
Поскольку  то этой ситуации соответствует точка 1 в области III на рис. 4.19, то есть область устойчивого вращения лишь при малых
то этой ситуации соответствует точка 1 в области III на рис. 4.19, то есть область устойчивого вращения лишь при малых 

Рис. 4.19

Рис. 4.20
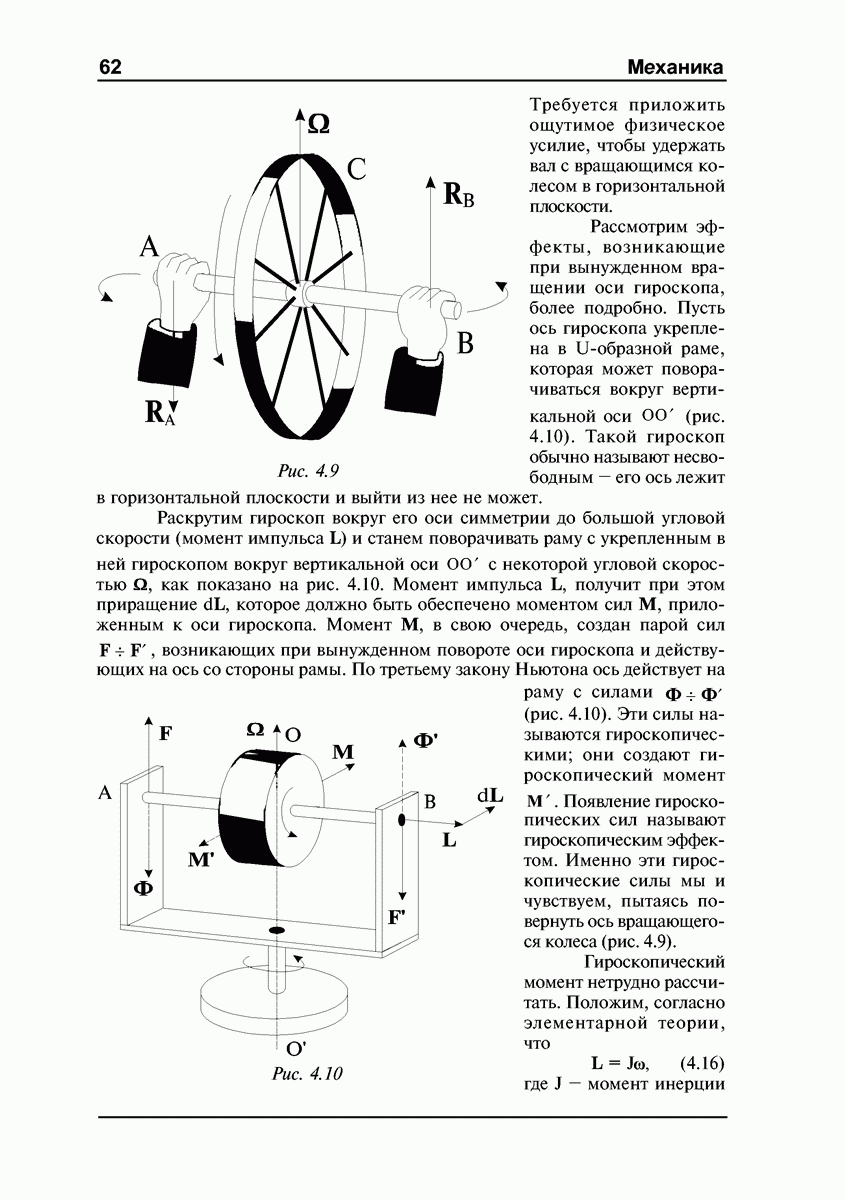
Таким образом, в нашем случае  вращение будет неустойчивым, и волчок перевернется на ножку (точка 2 в области II на рис. 4.19).
вращение будет неустойчивым, и волчок перевернется на ножку (точка 2 в области II на рис. 4.19).
Следует обратить внимание, что в процессе переворачивания волчка результирующий момент импульса сохраняет свое первоначальное направление, то есть вектор  все время направлен вертикально вверх. Это означает, что в ситуации, изображенной на рис. 4.20 б, когда ось волчка горизонтальна, вращение вокруг оси симметрии волчка отсутствует! Далее, при опрокидывании на ножку, вращение вокруг оси симметрии будет противоположно исходному (если смотреть все время со стороны ножки, рис. 4.20 в).
все время направлен вертикально вверх. Это означает, что в ситуации, изображенной на рис. 4.20 б, когда ось волчка горизонтальна, вращение вокруг оси симметрии волчка отсутствует! Далее, при опрокидывании на ножку, вращение вокруг оси симметрии будет противоположно исходному (если смотреть все время со стороны ножки, рис. 4.20 в).
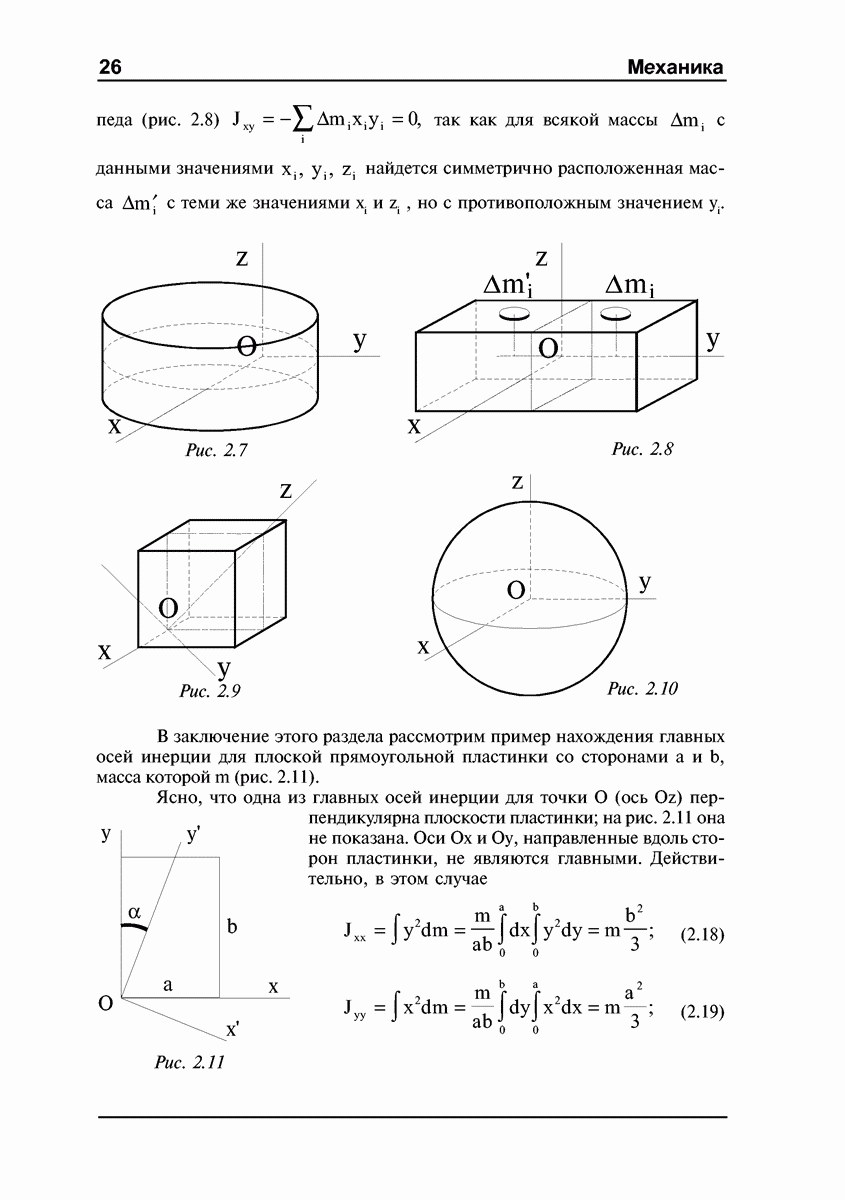
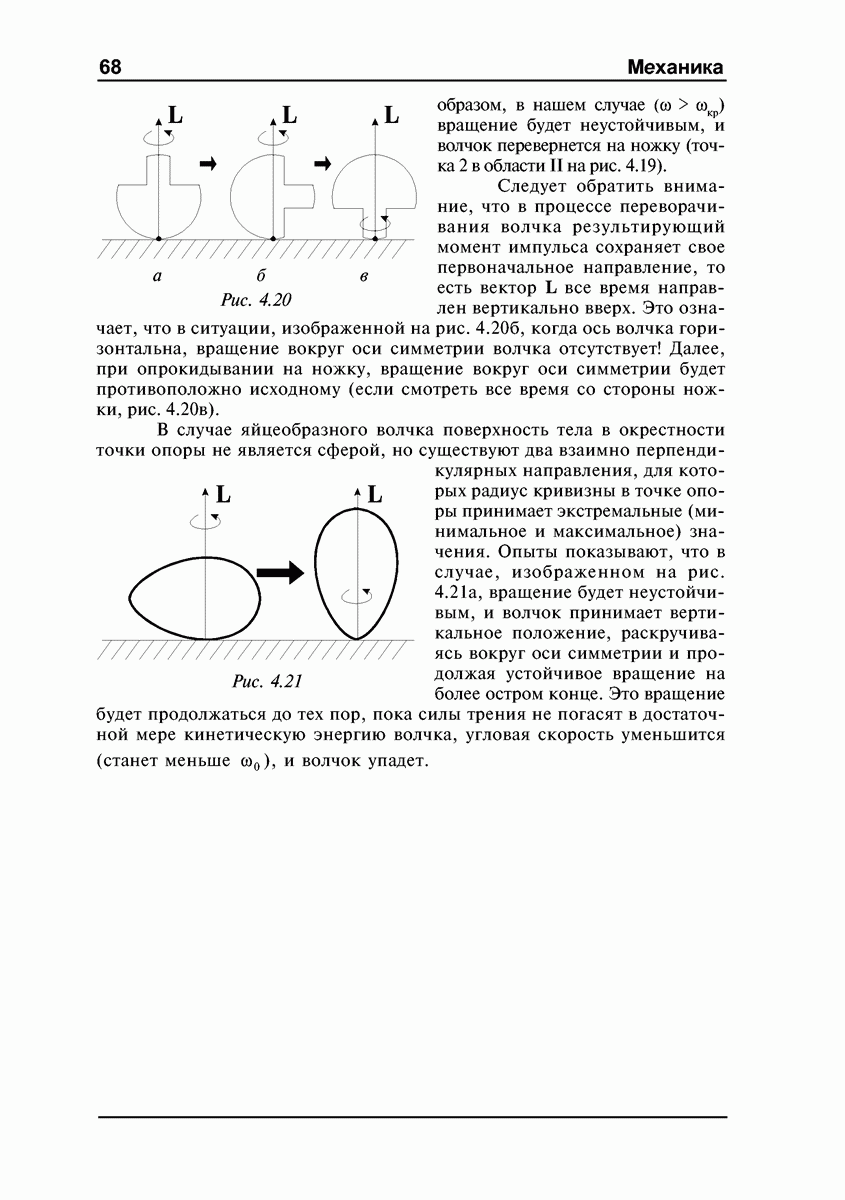
В случае яйцеобразного волчка поверхность тела в окрестности точки опоры не является сферой, но существуют два взаимно перпендикулярных направления, для которых радиус кривизны в точке опоры принимает экстремальные (минимальное и максимальное) значения. Опыты показывают, что в случае, изображенном на рис. 4.21 а, вращение будет неустойчивым, и волчок принимает вертикальное положение, раскручиваясь вокруг оси симметрии и продолжая устойчивое вращение на более остром конце. Это вращение будет продолжаться до тех пор, пока силы трения не погасят в достаточной мере кинетическую энергию волчка, угловая скорость уменьшится (станет меньше  ) и волчок упадет.
) и волчок упадет.

Рис. 4.21
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
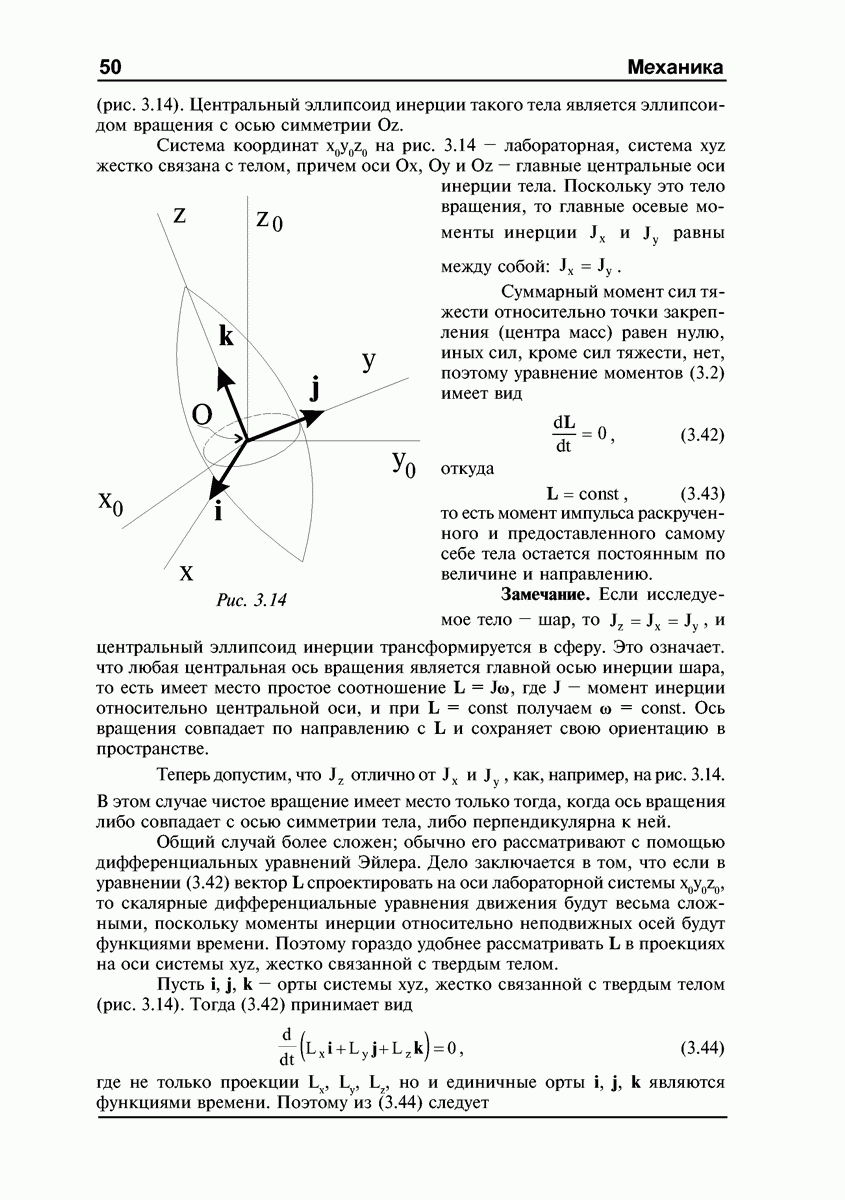
- ЛЕКЦИЯ №1. Кинематика абсолютно твердого тела. Степени свободы. Углы Эйлера. Поступательное движение. Вращение вокруг неподвижной оси. Плоское движение. Движение твердого тела, имеющего одну неподвижную точку. Движение свободного твердого тела.
- Поступательное движение
- Вращение вокруг неподвижной оси
- Плоское движение
- Движение твердого тела с одной неподвижной точкой.
- Движение свободного твердого тела.
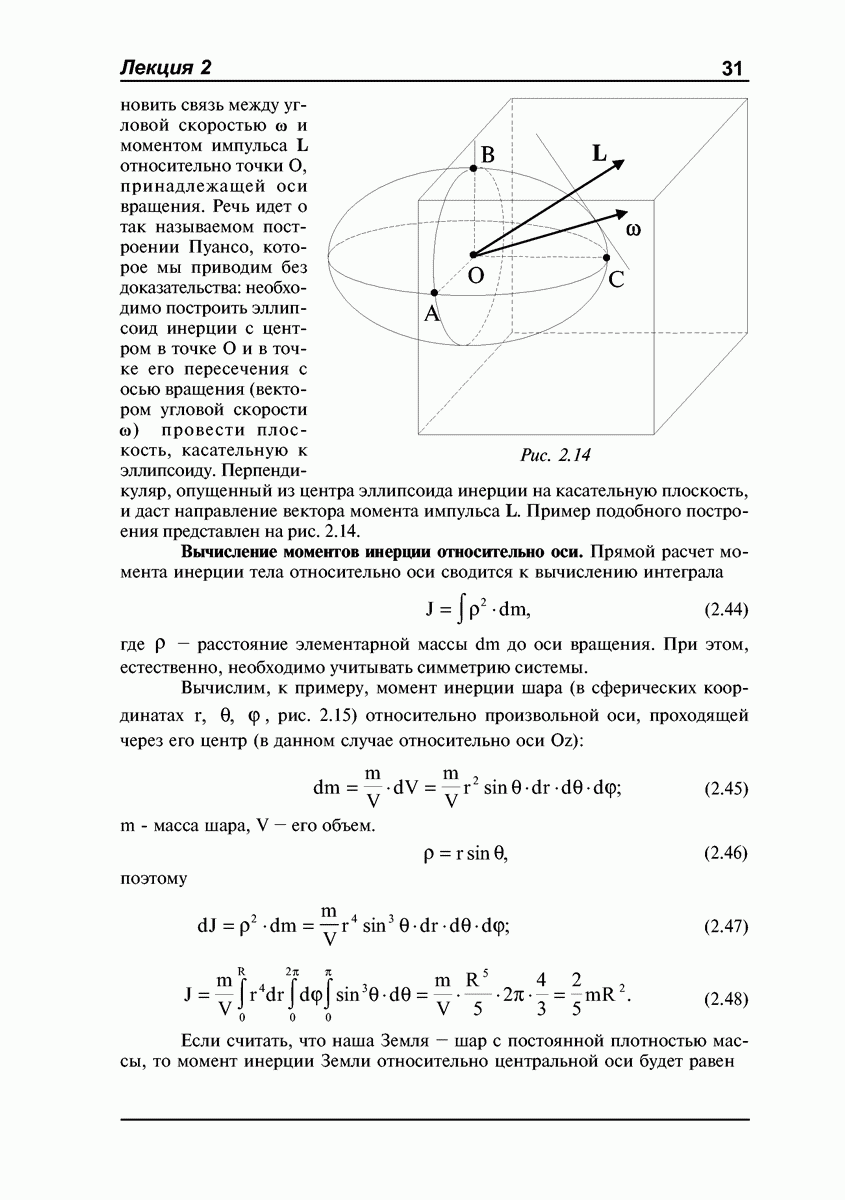
- ЛЕКЦИЯ №2. Динамика абсолютно твердого тела. Момент импульса. Тензор инерции. Момент импульса тела относительно оси. Эллипсоид инерции. Вычисление моментов инерции относительно оси. Теорема Гюйгенса-Штейнера. Момент импульса относительно движущегося центра масс.
- Главные оси инерции.
- Момент импульса твердого тела относительно оси. Момент инерции относительно оси.
- Эллипсоид инерции.
- Вычисление моментов инерции относительно оси.
- Теорема Гюйгенса-Штейнера.
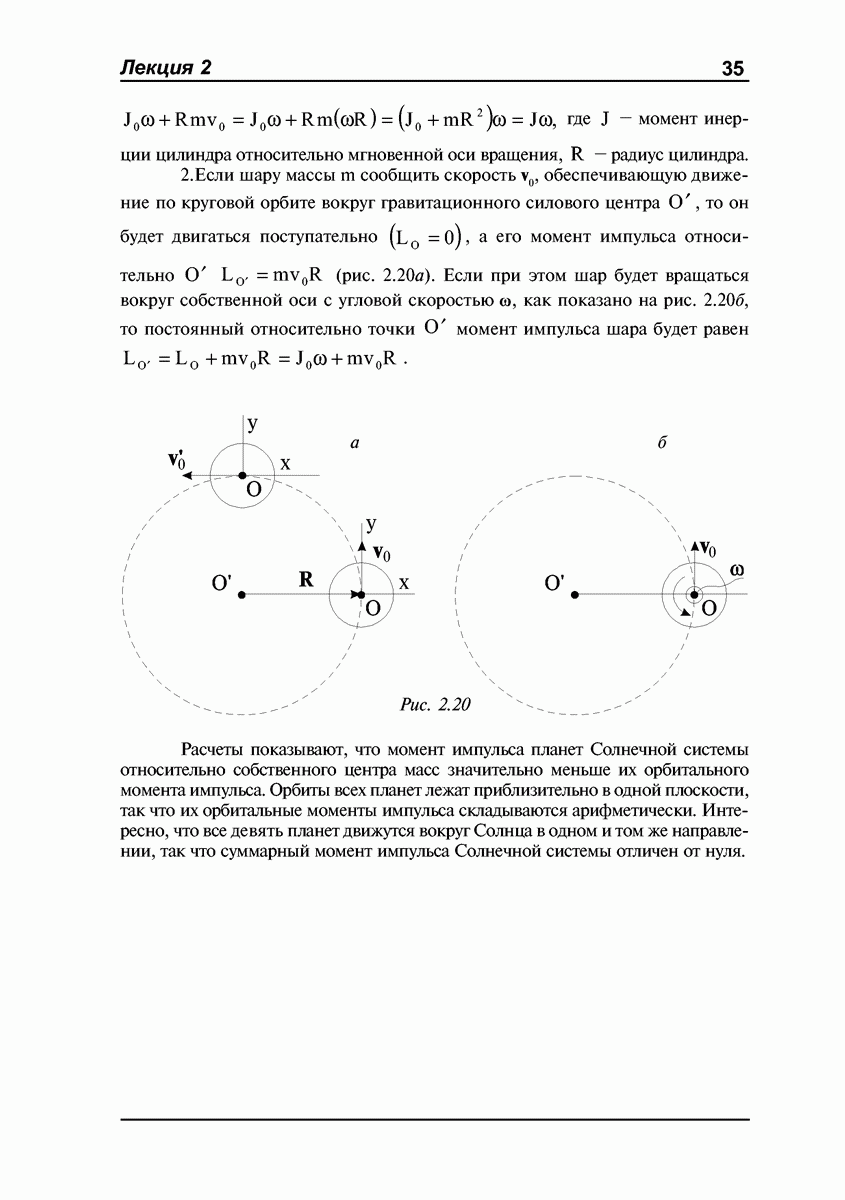
- Момент импульса тела относительно движущегося центра масс.
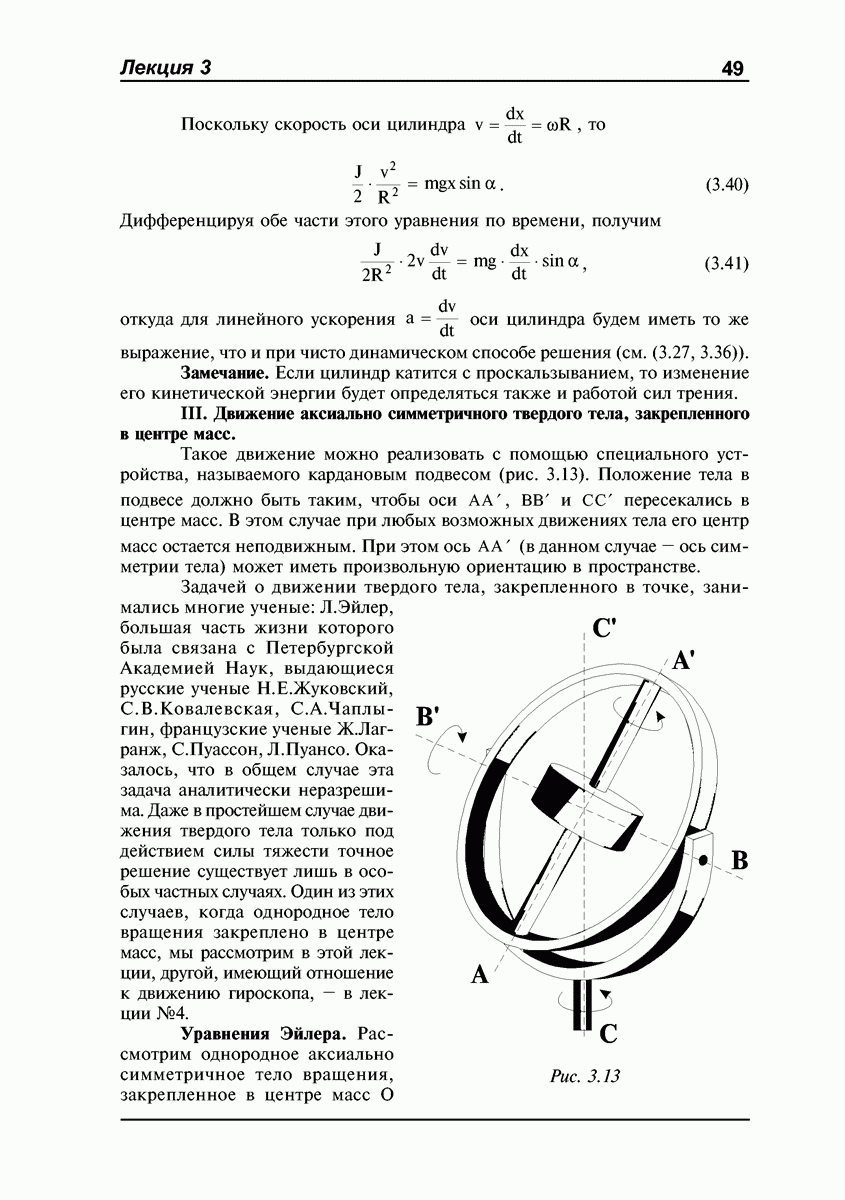
- ЛЕКЦИЯ №3. Динамика абсолютно твердого тела. Уравнение поступательного движения и уравнение моментов. Вращение твердого тела вокруг неподвижной оси. Центр удара. Динамика плоского движения твердого тела. Движение аксиально симметричного твердого тела, закрепленного в центре масс. Уравнения Эйлера.
- Уравнения динамики твердого тела. Общий случай.
- Кинетическая энергия вращающегося тела и работа внешних сил (ось вращения неподвижна).
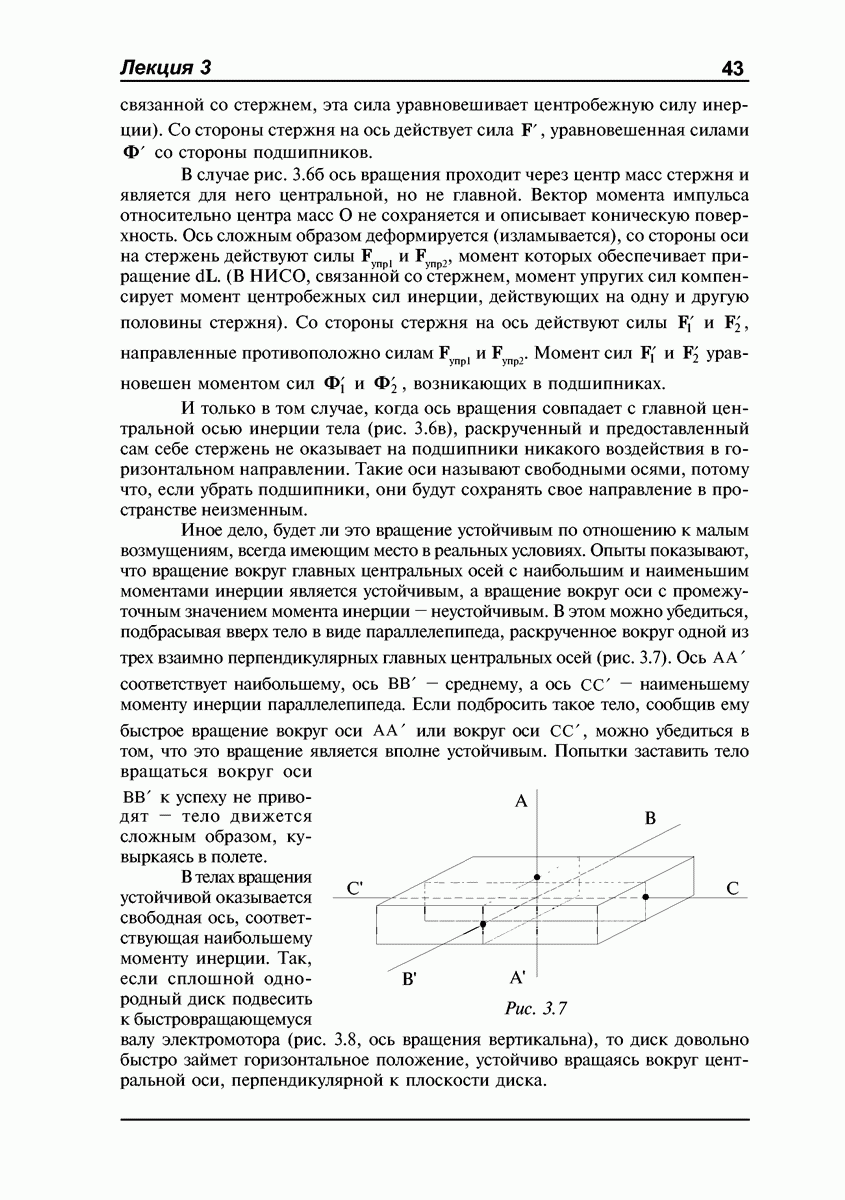
- Свободные оси. Устойчивость свободного вращения.
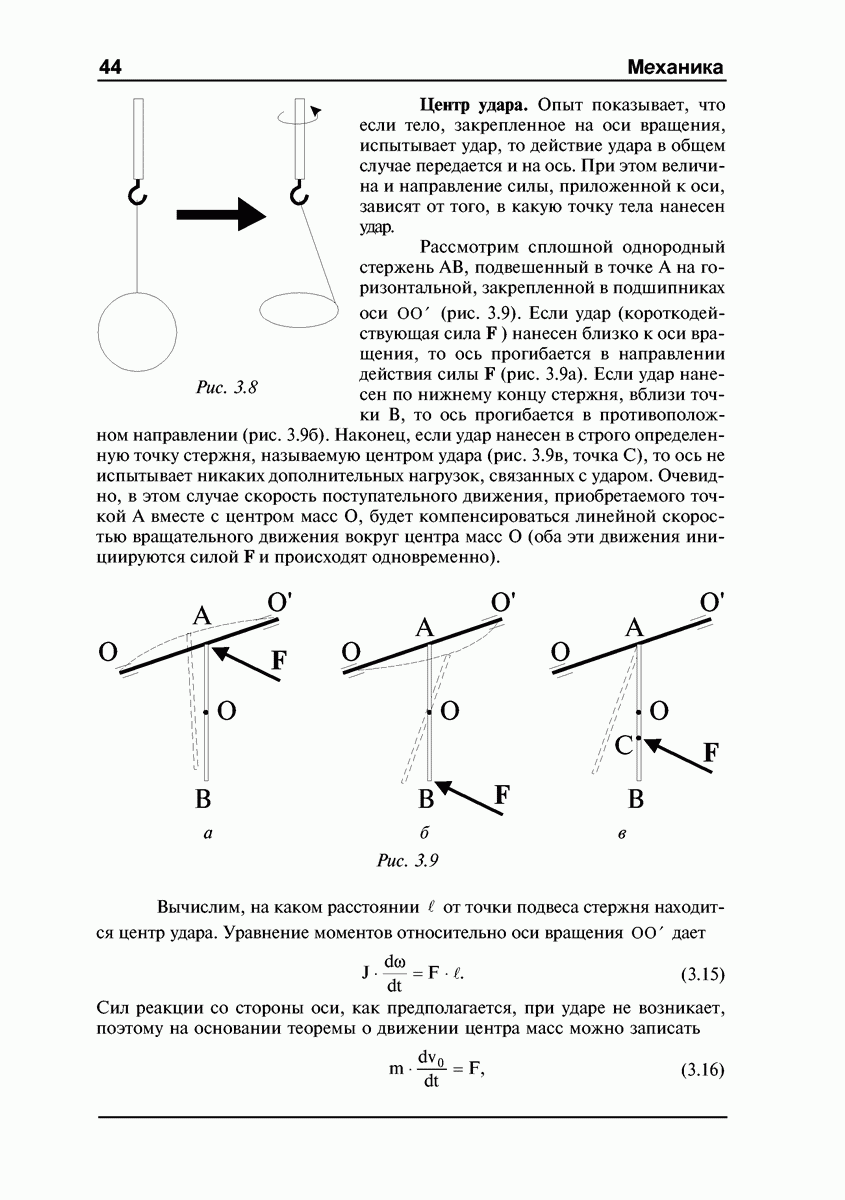
- Центр удара.
- Кинетическая энергия при плоском движении.
- Уравнения Эйлера.
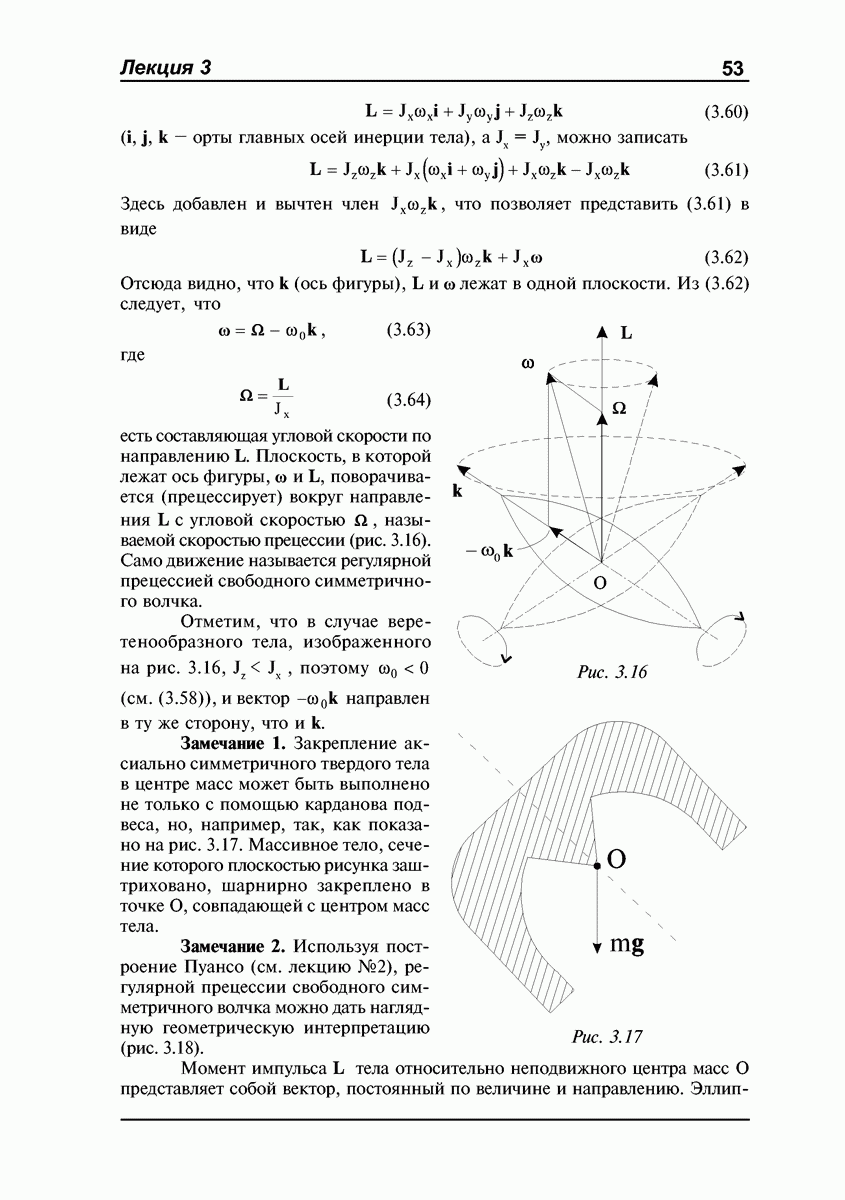
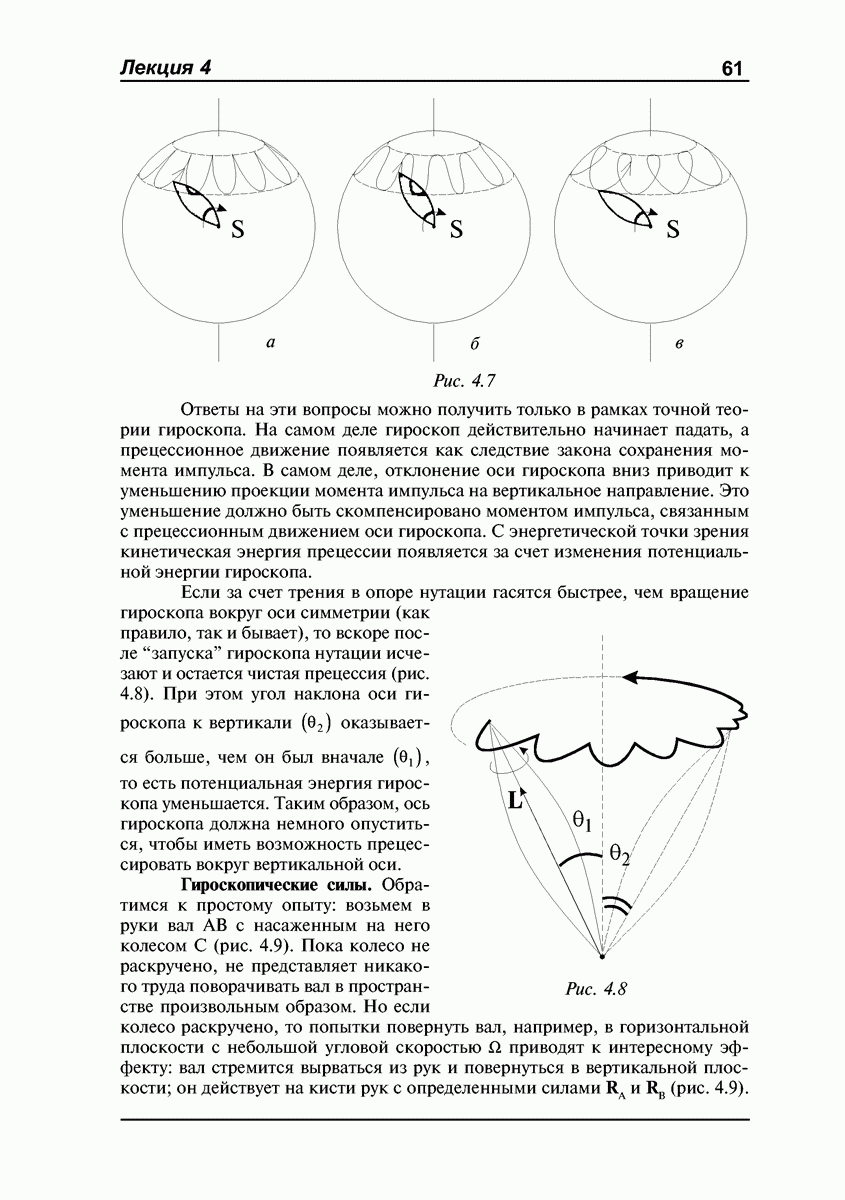
- ЛЕКЦИЯ №4. Гироскопы. Свободный гироскоп. Прецессия гироскопа под действием внешних сил. Угловая скорость прецессии. Нутации. Гироскопические силы, их природа и проявления.
- Свободный гироскоп.
- Прецессия гироскопа под действием внешних сил. Элементарная теория.
- Прецессия гироскопа под действием внешних сил. Отход от элементарной теории. Нутации.
- Гироскопические силы.
- Волчки.
- ЛИТЕРАТУРА