| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
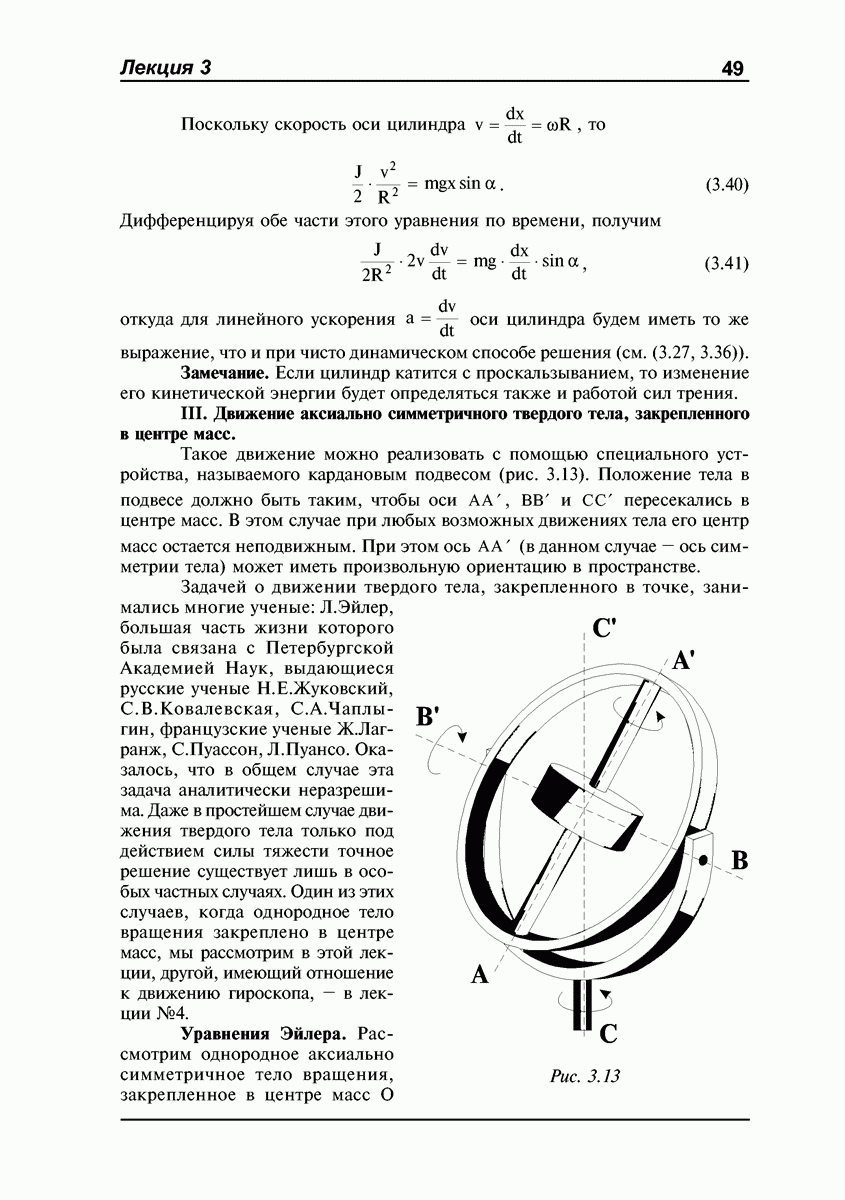
ЛЕКЦИЯ №1. Кинематика абсолютно твердого тела. Степени свободы. Углы Эйлера. Поступательное движение. Вращение вокруг неподвижной оси. Плоское движение. Движение твердого тела, имеющего одну неподвижную точку. Движение свободного твердого тела.
Механика твердого тела — один из наиболее трудных разделов курса. Как и механика материальной точки, он состоит из двух основных частей: кинематики и динамики.
Задача кинематики — дать способы описания движения твердого тела и, исходя из закона его движения, определить положение, скорость и ускорение любой точки тела в любой момент времени. В общем случае это довольно сложная задача — в этом можно убедиться, покрутив в руках, например, книгу или ручку. Конечно, всякое тело можно представить как систему материальных точек и попробовать применить к нему приемы, известные из кинематики точки. На первый взгляд, это не упрощает ситуацию — не выписывать же законы движения для всех физически малых частей, на которые можно разбить тело, пусть даже их будет и конечное число!
Облегчающее обстоятельство кроется в самих словах “твердое тело”. Твердое — значит практически недеформируемое. Опыт показывает, что если на какой-либо достаточно твердый предмет подействовать силой и заставить его двигаться, то расстояния между любыми его точками останутся неизменными. Хотя, конечно, под действием приложенных сил в теле возникнут внутренние напряжения, причина которых — деформации отдельных его частей. Но если мы говорим о твердом теле, то эти деформации оказываются настолько малыми, что незаметны для глаза, и от них можно отвлечься. В итоге мы приходим к идеализированной модели абсолютно твердого тела (в дальнейшем — просто твердого тела), которое совершенно не способно деформироваться, хотя под действием внешних сил в нем могут возникать определенные внутренние усилия.
Таким образом, твердое тело можно рассматривать как систему материальных точек, относительные положения которых остаются неизменными. Другими словами, все макроскопические элементы такого тела неподвижны в системе координат, жестко связанной с телом. Именно это обстоятельство позволяет значительно упростить решение кинематических задач и конкретизировать многие общие понятия (импульс, момент импульса, энергия), введенные ранее при рассмотрении системы материальных точек.
Степени свободы. Углы Эйлера.
Двигаясь в пространстве, твердое тело обладает определенными степенями свободы.
Число степеней свободы — это число независимых величин, которые необходимо задать для того, чтобы однозначно определить положение тела в пространстве. В разных ситуациях число степеней свободы твердого тела может быть различным. Если диск, не вращаясь, может скользить вдоль неподвижной в данной системе отсчета оси (рис. 1.1а), то в данной системе отсчета он, очевидно, обладает только одной степенью свободы — положение диска однозначно определяется, скажем, координатой х его центра, отсчитываемой вдоль оси. Но если диск, кроме того, может еще и вращаться (рис. 1.16),

Рис. 1.1
то он приобретает еще одну степень свободы — к координате  добавляется угол
добавляется угол  поворота диска вокруг оси. Если ось с диском зажата в рамке, которая может поворачиваться вокруг вертикальной оси (рис. 1.1в), то число степеней свободы становится равным трем — к
поворота диска вокруг оси. Если ось с диском зажата в рамке, которая может поворачиваться вокруг вертикальной оси (рис. 1.1в), то число степеней свободы становится равным трем — к  добавляется угол
добавляется угол  поворота рамки.
поворота рамки.
Коробка, которая может перемещаться по поверхности стола (рис. 1.2), также обладает тремя степенями свободы — для однозначного определения ее положения можно задать, например, координаты  ее центра и угол
ее центра и угол  между одним из ребер коробки и краем стола.
между одним из ребер коробки и краем стола.
Каково же число степеней свободы твердого тела в самом общем случае?
Для того, чтобы однозначно задать положение твердого тела в пространстве, надо зафиксировать три его точки, не лежащие на одной прямой. Одна материальная точка имеет три степени свободы (три декартовы координаты  Две материальные точки, жестко связанные между собой, имеют 3 + 3 - 1 = 5 степеней свободы. В этом случае координаты точек
Две материальные точки, жестко связанные между собой, имеют 3 + 3 - 1 = 5 степеней свободы. В этом случае координаты точек  не являются независимыми величинами, так как имеется уравнение связи
не являются независимыми величинами, так как имеется уравнение связи

где  — расстояние между точками.
— расстояние между точками.
Таким образом, в общем случае для твердого тела получаем 3 + 3 + 3 -3 = 6 степеней свободы. При этом имеются три уравнения связи, выражающие постоянство расстояний между каждой парой точек.
Шесть параметров, соответствующих шести степеням свободы твердого тела, можно задавать по-разному. В дальнейшем мы будем пользоваться тремя различными декартовыми системами координат:
1. Лабораторная система 
2. Система  начало которой связано с некоторой точкой О твердого тела, а оси остаются параллельными осям лабораторной системы
начало которой связано с некоторой точкой О твердого тела, а оси остаются параллельными осям лабораторной системы 

Рис. 1.2
то есть система  движется вместе с точкой О твердого тела относительно системы
движется вместе с точкой О твердого тела относительно системы  поступательно.
поступательно.
3. Система  начало которой находится в той же точке О, что и начало системы
начало которой находится в той же точке О, что и начало системы  а оси жестко связаны с твердым телом.
а оси жестко связаны с твердым телом.
Тогда шести степеням свободы тела будут соответствовать, во-первых, три координаты точки О (в лабораторной системе XYZ), а во-вторых, — три угла  однозначно определяющие положение системы
однозначно определяющие положение системы  относительно
относительно  Эти углы называются углами Эйлера.
Эти углы называются углами Эйлера.
Их смысл ясен из рис. 1.3, где  — линия пересечения плоскостей
— линия пересечения плоскостей  при этом нижнее основание твердого тела (прямоугольного параллелепипеда) лежит в плоскости
при этом нижнее основание твердого тела (прямоугольного параллелепипеда) лежит в плоскости  Обычно их называют так:
Обычно их называют так:  — угол собственного вращения (с изменением этого угла связан поворот твердого тела вокруг оси z),
— угол собственного вращения (с изменением этого угла связан поворот твердого тела вокруг оси z),  — угол прецессии (поворот вокруг
— угол прецессии (поворот вокруг  с сохранением угла
с сохранением угла  между осями
между осями  ),
),  — угол нутации (отклонение тела от оси
— угол нутации (отклонение тела от оси  ).
).
Примеры с диском на оси и коробкой (рис. 1.1, 1.2) показывают, что сложное движение того или иного тела может быть представлено как суперпозиция достаточно простых движений: поступательного перемещения и поворота (вращения) вокруг оси. В дальнейшем, следуя принципу “от простого к сложному”, мы рассмотрим 5 типов движения твердого тела, исчерпывающих все встречающиеся на практике случаи:
— поступательное движение;
— вращение вокруг неподвижной оси;
— плоское, или плоско-параллельное движение;
— движение твердого тела с одной неподвижной точкой (такое движение иногда называют сферическим);
— движение свободного, то есть незакрепленного твердого тела.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- ЛЕКЦИЯ №1. Кинематика абсолютно твердого тела. Степени свободы. Углы Эйлера. Поступательное движение. Вращение вокруг неподвижной оси. Плоское движение. Движение твердого тела, имеющего одну неподвижную точку. Движение свободного твердого тела.
- Поступательное движение
- Вращение вокруг неподвижной оси
- Плоское движение
- Движение твердого тела с одной неподвижной точкой.
- Движение свободного твердого тела.
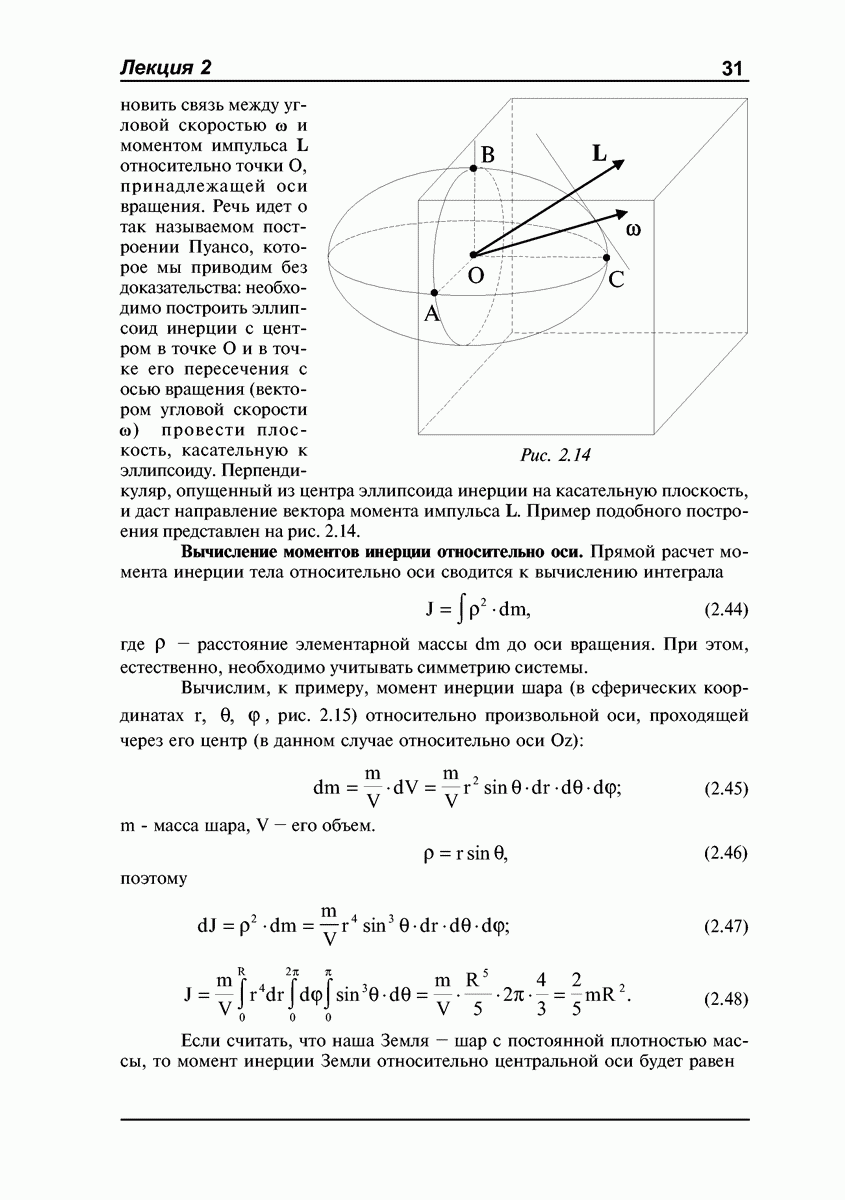
- ЛЕКЦИЯ №2. Динамика абсолютно твердого тела. Момент импульса. Тензор инерции. Момент импульса тела относительно оси. Эллипсоид инерции. Вычисление моментов инерции относительно оси. Теорема Гюйгенса-Штейнера. Момент импульса относительно движущегося центра масс.
- Главные оси инерции.
- Момент импульса твердого тела относительно оси. Момент инерции относительно оси.
- Эллипсоид инерции.
- Вычисление моментов инерции относительно оси.
- Теорема Гюйгенса-Штейнера.
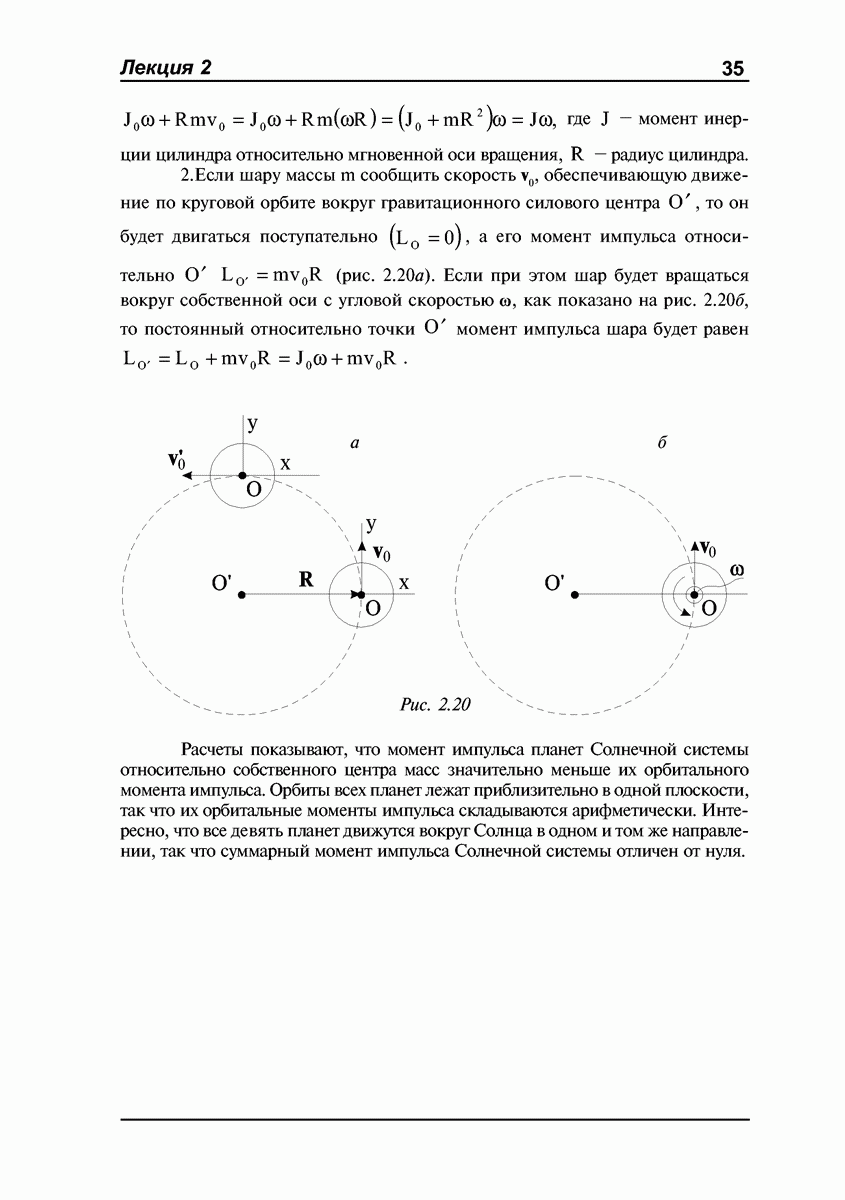
- Момент импульса тела относительно движущегося центра масс.
- ЛЕКЦИЯ №3. Динамика абсолютно твердого тела. Уравнение поступательного движения и уравнение моментов. Вращение твердого тела вокруг неподвижной оси. Центр удара. Динамика плоского движения твердого тела. Движение аксиально симметричного твердого тела, закрепленного в центре масс. Уравнения Эйлера.
- Уравнения динамики твердого тела. Общий случай.
- Кинетическая энергия вращающегося тела и работа внешних сил (ось вращения неподвижна).
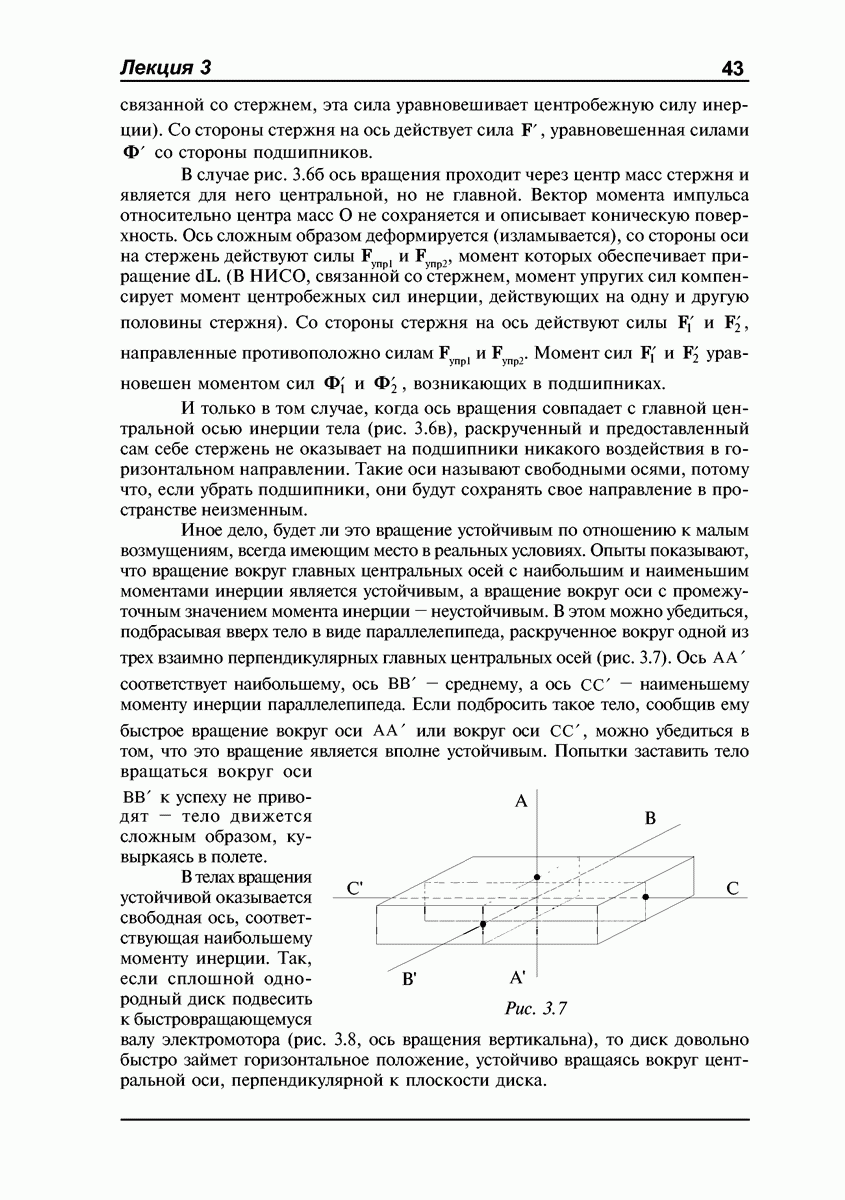
- Свободные оси. Устойчивость свободного вращения.
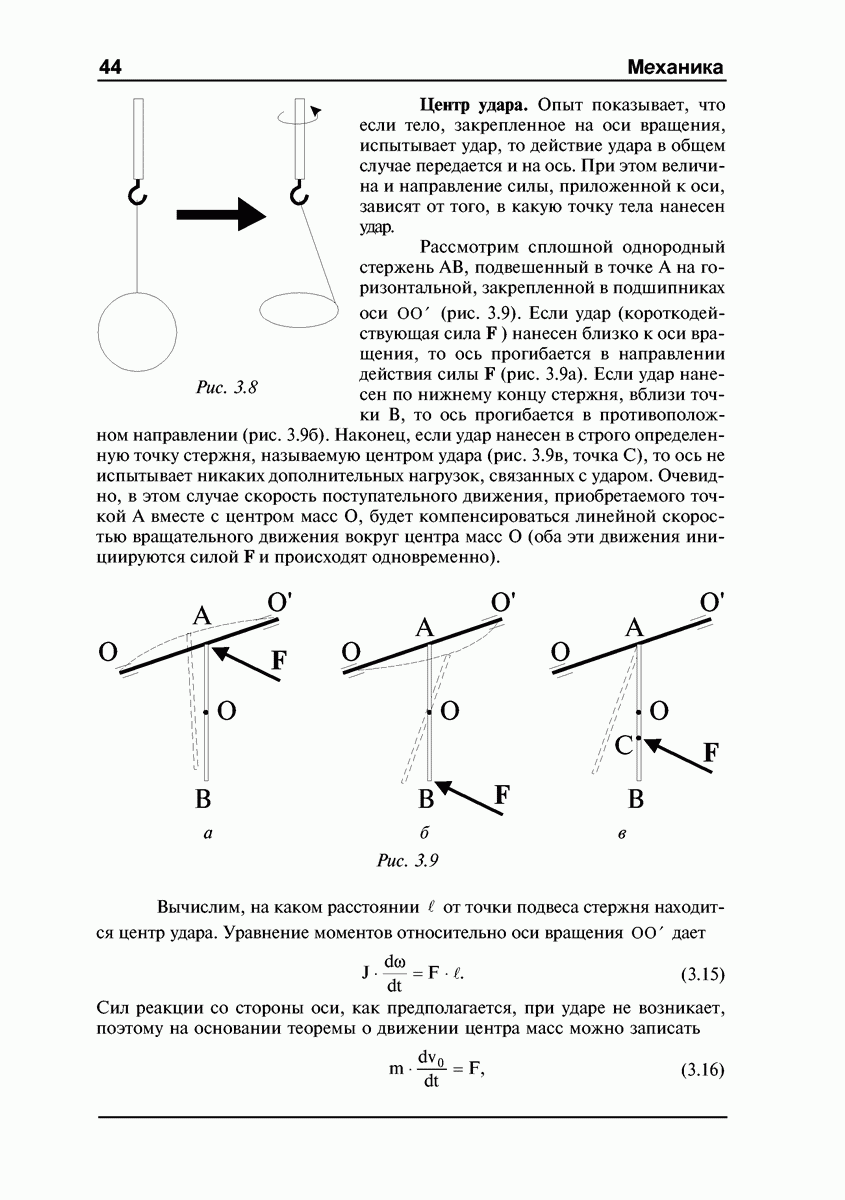
- Центр удара.
- Кинетическая энергия при плоском движении.
- Уравнения Эйлера.
- ЛЕКЦИЯ №4. Гироскопы. Свободный гироскоп. Прецессия гироскопа под действием внешних сил. Угловая скорость прецессии. Нутации. Гироскопические силы, их природа и проявления.
- Свободный гироскоп.
- Прецессия гироскопа под действием внешних сил. Элементарная теория.
- Прецессия гироскопа под действием внешних сил. Отход от элементарной теории. Нутации.
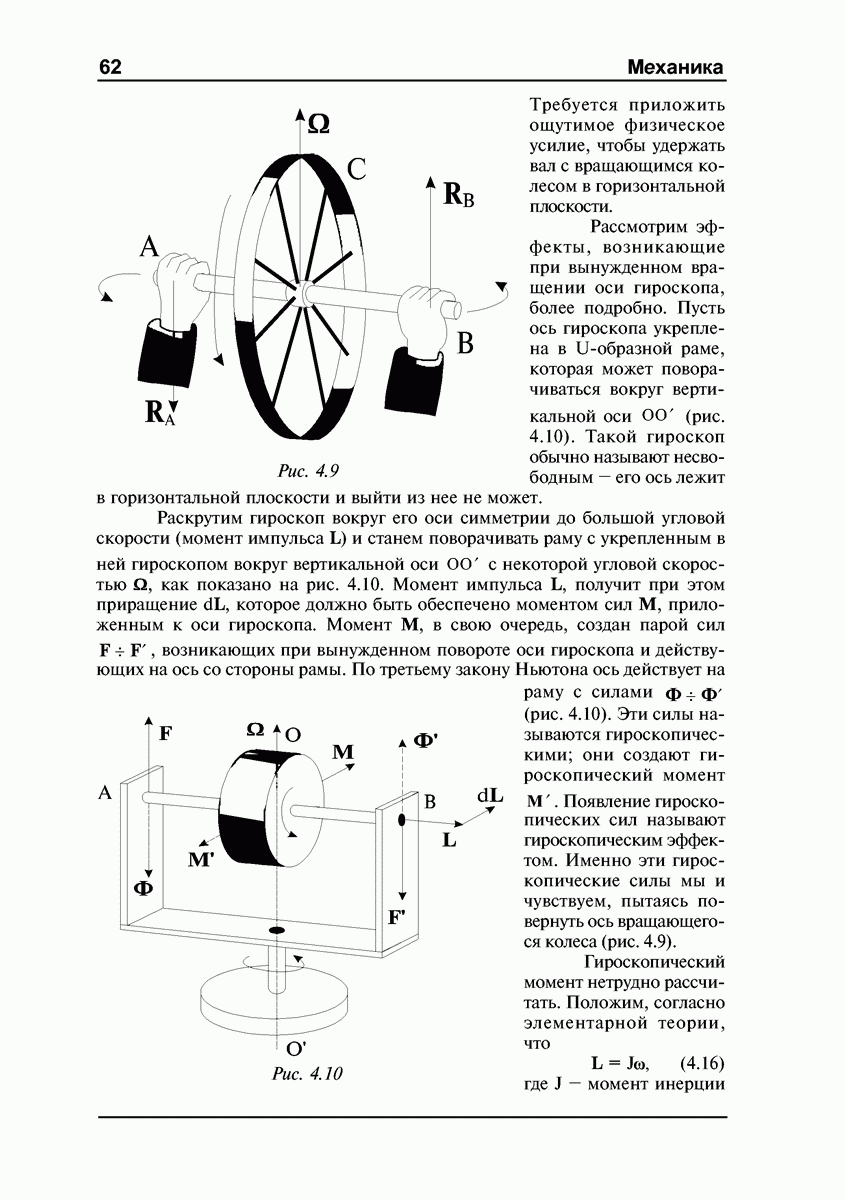
- Гироскопические силы.
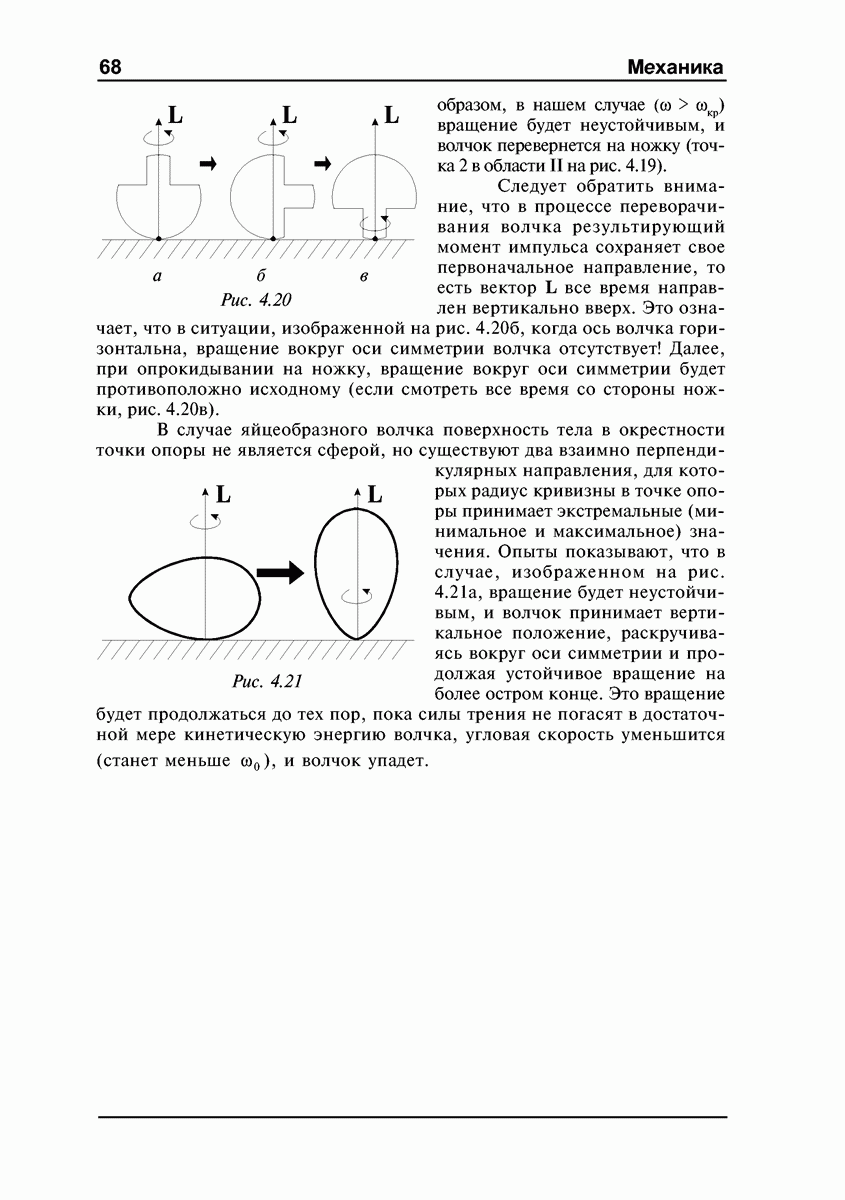
- Волчки.
- ЛИТЕРАТУРА