| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
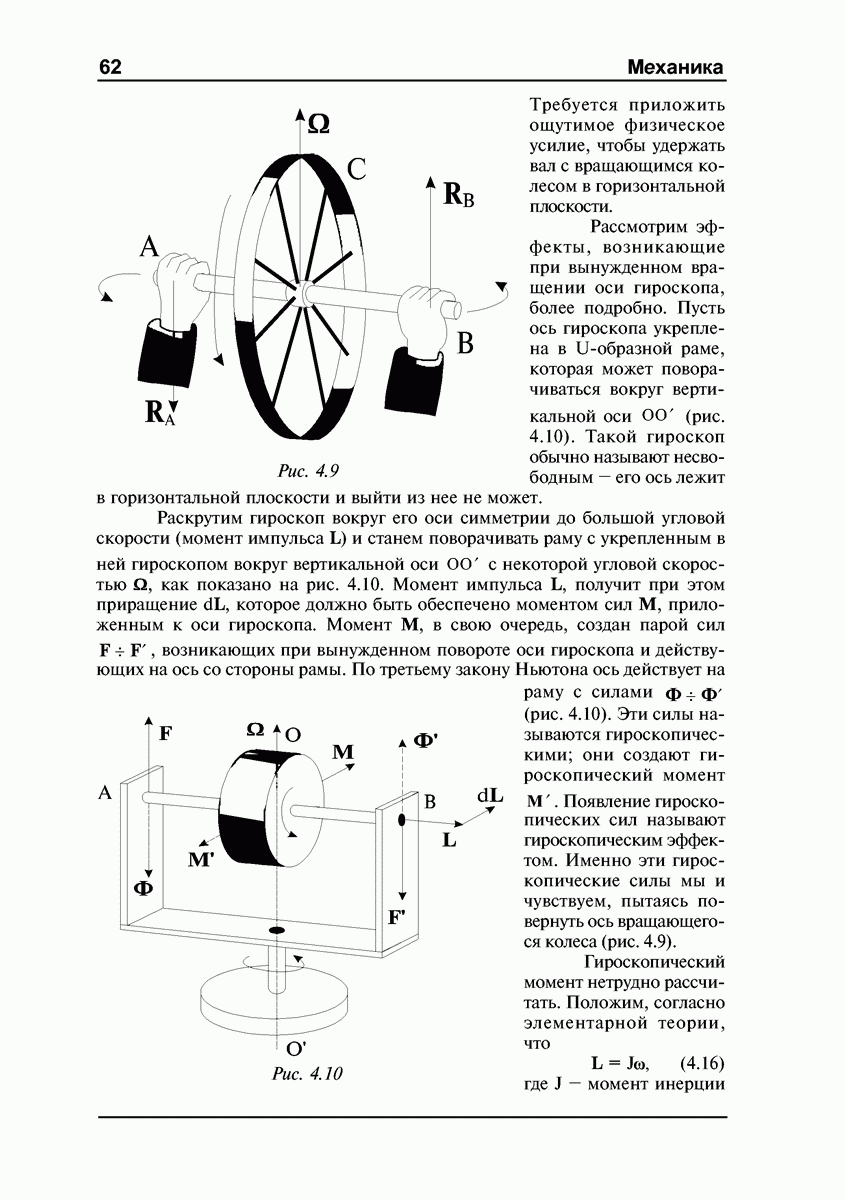
Прецессия гироскопа под действием внешних сил. Элементарная теория.
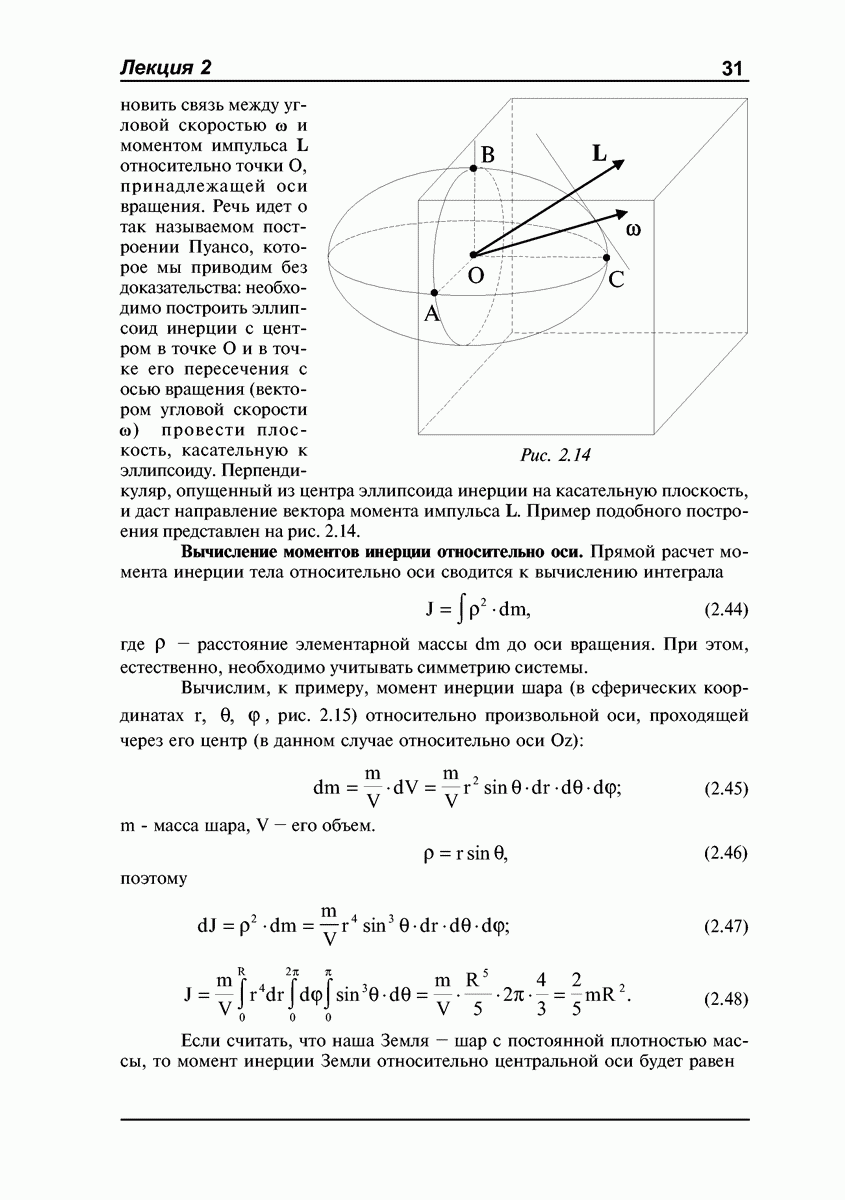
Рассмотрим теперь ситуацию, когда к оси гироскопа приложена сила, линия действия которой не проходит через точку закрепления. Опыты показывают, что в этом случае гироскоп ведет себя весьма необычным образом.
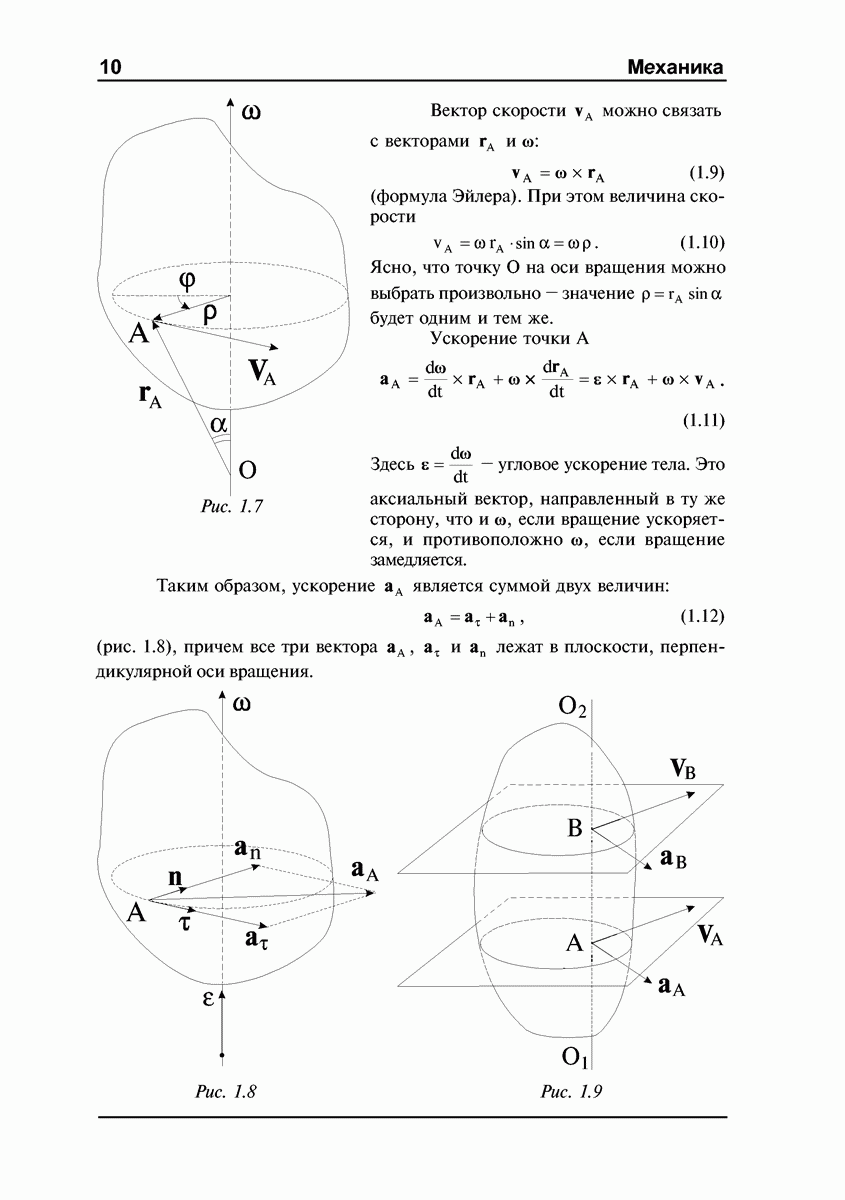
Если к оси шарнирно закрепленного в точке О гироскопа (рис. 4.3) прикрепить пружину и тянуть за нее вверх с силой  то ось гироскопа будет перемещаться не в направлении силы, а перпендикулярно к ней, вбок. Это движение называется прецессией гироскопа под действием внешней силы.
то ось гироскопа будет перемещаться не в направлении силы, а перпендикулярно к ней, вбок. Это движение называется прецессией гироскопа под действием внешней силы.
Опытным путем можно установить, что угловая скорость прецессии зависит не только от величины силы  (рис. 4.3), но и от того, к какой точке оси гироскопа эта сила приложена: с увеличением
(рис. 4.3), но и от того, к какой точке оси гироскопа эта сила приложена: с увеличением  и ее плеча
и ее плеча  относительно точки закрепления О скорость прецессии увеличивается. При этом оказывается, что чем сильнее раскручен гироскоп, тем меньше угловая скорость прецессии при данных
относительно точки закрепления О скорость прецессии увеличивается. При этом оказывается, что чем сильнее раскручен гироскоп, тем меньше угловая скорость прецессии при данных 
В качестве силы  вызывающей прецессию, может выступать сила тяжести, если точка закрепления гироскопа
вызывающей прецессию, может выступать сила тяжести, если точка закрепления гироскопа

Рис. 4.3

Рис. 4.4
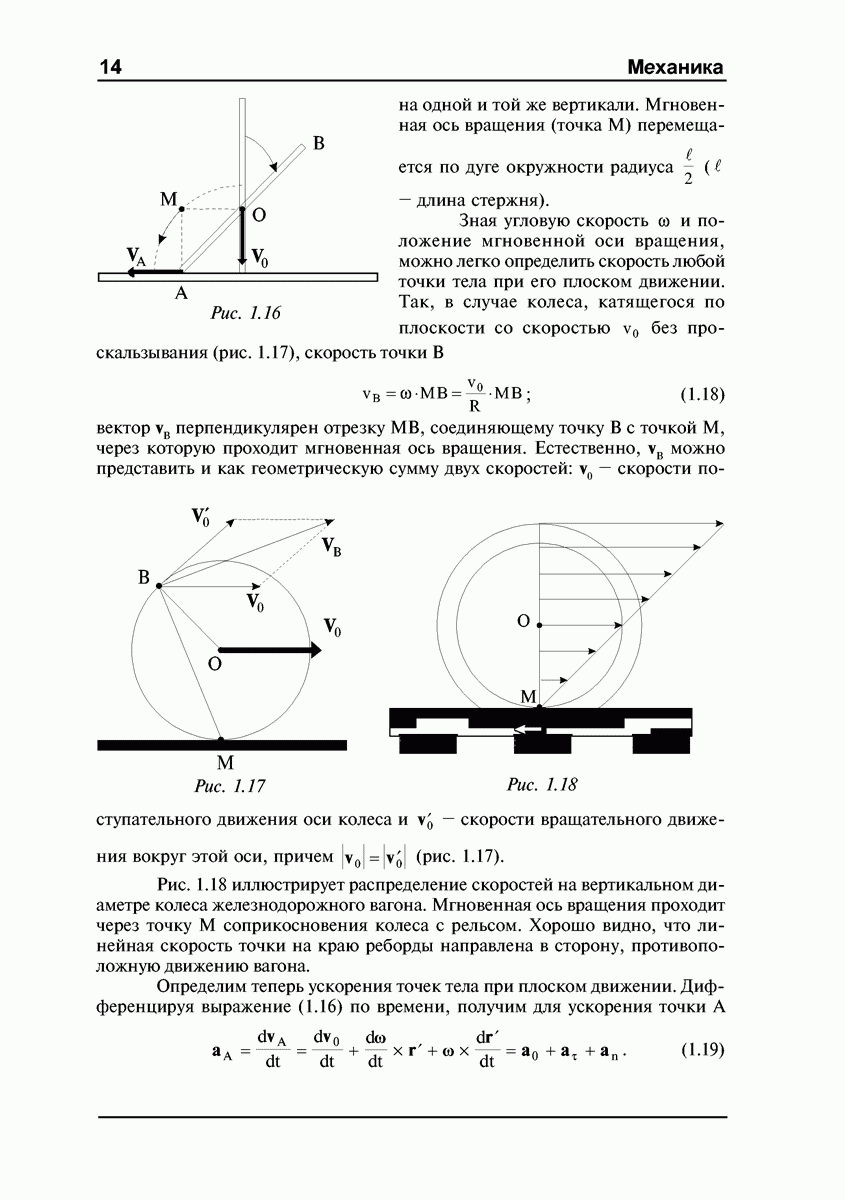
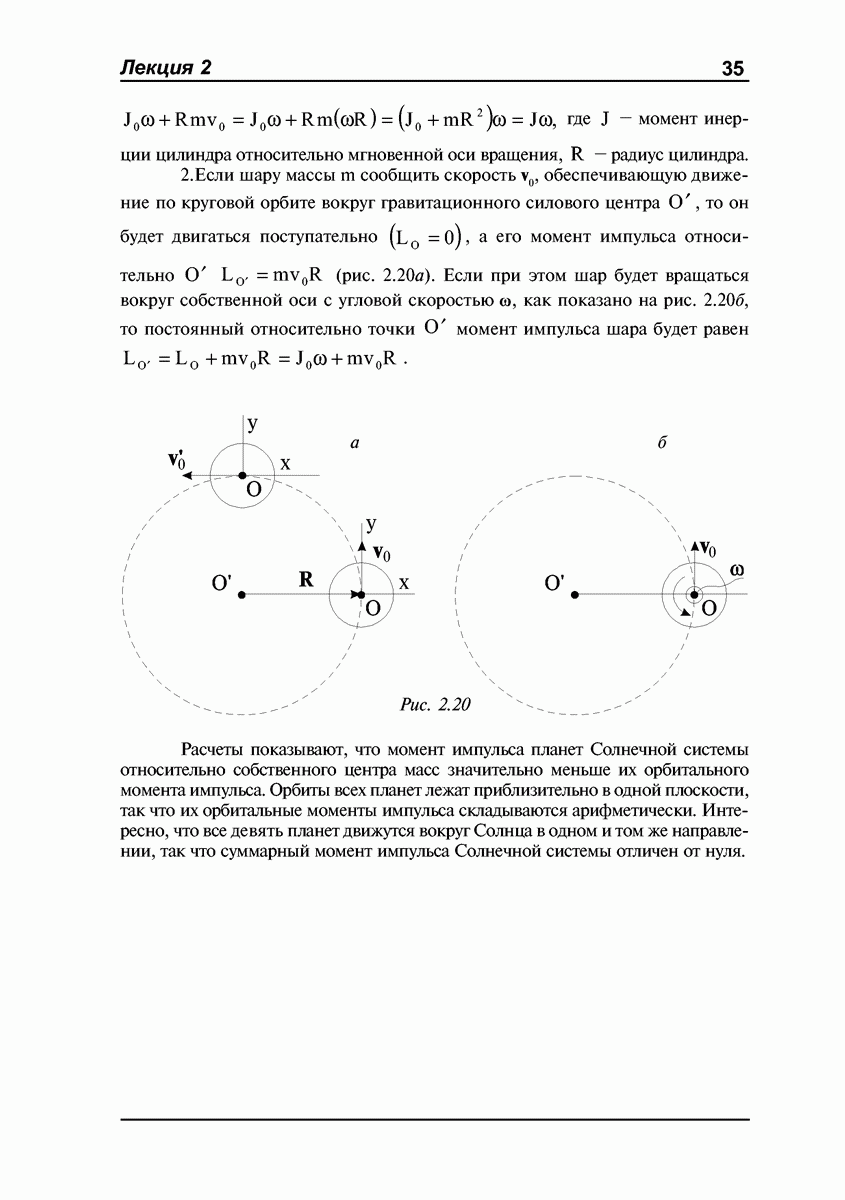
не совпадает с центром масс. Так, если стержень с быстро вращающимся диском подвесить на нитке (рис. 4.4), то он не опускается вниз, как это можно было бы предположить, а совершает прецессионное движение вокруг нитки. Наблюдение прецессии гироскопа под действием силы тяжести в некотором смысле даже удобнее — линия действия силы “автоматически” смещается вместе с осью гироскопа, сохраняя свою ориентацию в пространстве.
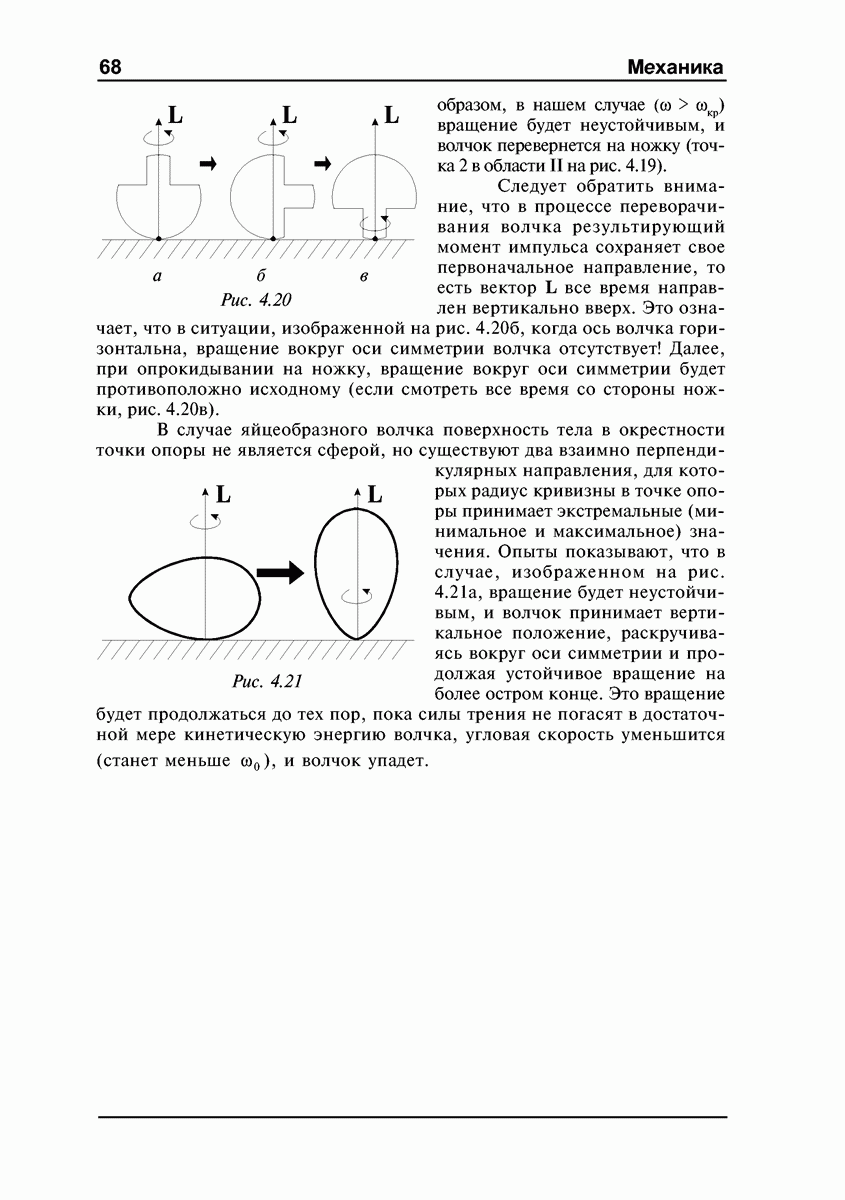
Можно привести и другие примеры прецессии — например, движение оси хорошо известной детской игрушки — юлы с заостренным концом (рис. 4.5). Юла, раскрученная вокруг своей оси и поставленная на горизонтальную плоскость слегка наклонно, начинает прецессировать вокруг вертикальной оси под действием силы тяжести (рис. 4.5).
Точное решение задачи о движении гироскопа в поле внешних сил довольно сложно. Однако, выражение для угловой скорости прецессии можно легко получить в рамках так называемой элементарной теории гироскопа. В этой теории делается допущение, что мгновенная угловая скорость вращения гироскопа и его момент импульса направлены вдоль оси симметрии гироскопа. Другими словами, предполагается, что угловая скорость вращения гироскопа вокруг своей оси значительно больше угловой скорости прецессии:

так что вкладом в  обусловленным прецессионным движением гироскопа, можно пренебречь. В этом приближении момент импульса гироскопа, очевидно, равен
обусловленным прецессионным движением гироскопа, можно пренебречь. В этом приближении момент импульса гироскопа, очевидно, равен

где  момент инерции относительно оси симметрии.
момент инерции относительно оси симметрии.
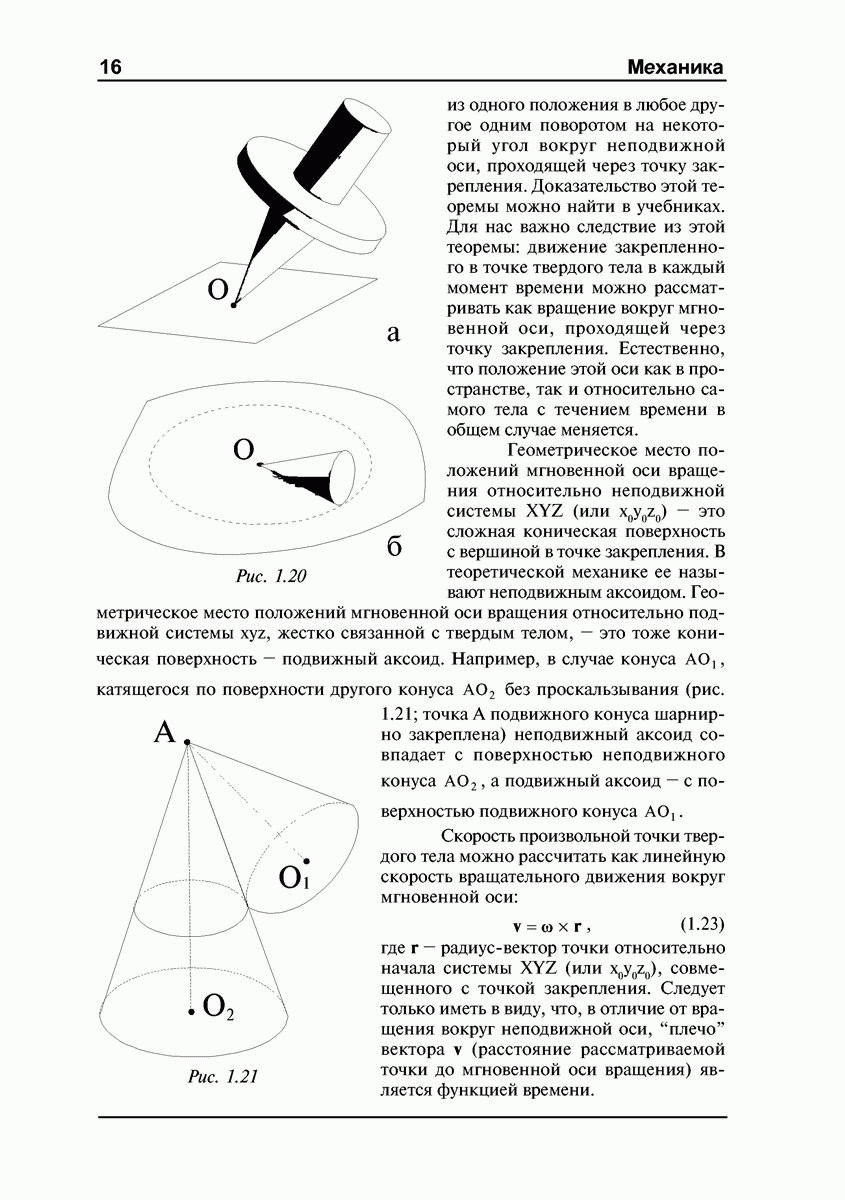
Итак, рассмотрим тяжелый симметричный гироскоп, у которого неподвижная точка  (точка опоры о подставку) не совпадает с центром масс О (рис. 4.6).
(точка опоры о подставку) не совпадает с центром масс О (рис. 4.6).
Момент силы тяжести относительно точки 


Рис. 4.5

Рис. 4.6
где  — угол между вертикалью и осью симметрии гироскопа. Вектор М направлен по нормали к плоскости, в которой лежат ось симметрии гироскопа и вертикаль, проведенная через точку
— угол между вертикалью и осью симметрии гироскопа. Вектор М направлен по нормали к плоскости, в которой лежат ось симметрии гироскопа и вертикаль, проведенная через точку  (рис. 4.6). Сила реакции опоры проходит через
(рис. 4.6). Сила реакции опоры проходит через  и ее момент относительно этой точки равен нулю.
и ее момент относительно этой точки равен нулю.
Изменение момента импульса  определяется выражением
определяется выражением

При этом и  и ось волчка прецессируют вокруг вертикального направления с угловой скоростью
и ось волчка прецессируют вокруг вертикального направления с угловой скоростью 
Еще раз подчеркнем: делается допущение, что выполнено условие (4.5) и что  постоянно направлен вдоль оси симметрии гироскопа. Из рис. 4.6 следует, что
постоянно направлен вдоль оси симметрии гироскопа. Из рис. 4.6 следует, что

В векторном виде

Сравнивая (4.8) и (4.10), получаем следующую связь между моментом силы М, моментом импульса  и угловой скоростью прецессии
и угловой скоростью прецессии 

Это соотношение позволяет определить направление прецессии при заданном направлении вращения волчка вокруг своей оси.
Обратим внимание, что М определяет угловую скорость прецессии, а не угловое ускорение, поэтому мгновенное «выключение» М приводит к мгновенному же исчезновению прецессии, то есть прецессионное движение является безынерционным.
Сила, вызывающая прецессионное движение, может иметь любую природу. Для поддержания этого движения важно, чтобы вектор момента силы  поворачивался вместе с осью гироскопа. Как уже было отмечено, в случае силы тяжести это достигается автоматически. При этом из (4.11) с учетом того, что в нашем приближении справедливо соотношение (4.6), можно получить:
поворачивался вместе с осью гироскопа. Как уже было отмечено, в случае силы тяжести это достигается автоматически. При этом из (4.11) с учетом того, что в нашем приближении справедливо соотношение (4.6), можно получить:

Отсюда для угловой скорости прецессии получаем

Следует отметить, что  не зависит от угла
не зависит от угла  наклона оси гироскопа и обратно пропорциональна
наклона оси гироскопа и обратно пропорциональна  что хорошо согласуется с опытными данными.
что хорошо согласуется с опытными данными.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- ЛЕКЦИЯ №1. Кинематика абсолютно твердого тела. Степени свободы. Углы Эйлера. Поступательное движение. Вращение вокруг неподвижной оси. Плоское движение. Движение твердого тела, имеющего одну неподвижную точку. Движение свободного твердого тела.
- Поступательное движение
- Вращение вокруг неподвижной оси
- Плоское движение
- Движение твердого тела с одной неподвижной точкой.
- Движение свободного твердого тела.
- ЛЕКЦИЯ №2. Динамика абсолютно твердого тела. Момент импульса. Тензор инерции. Момент импульса тела относительно оси. Эллипсоид инерции. Вычисление моментов инерции относительно оси. Теорема Гюйгенса-Штейнера. Момент импульса относительно движущегося центра масс.
- Главные оси инерции.
- Момент импульса твердого тела относительно оси. Момент инерции относительно оси.
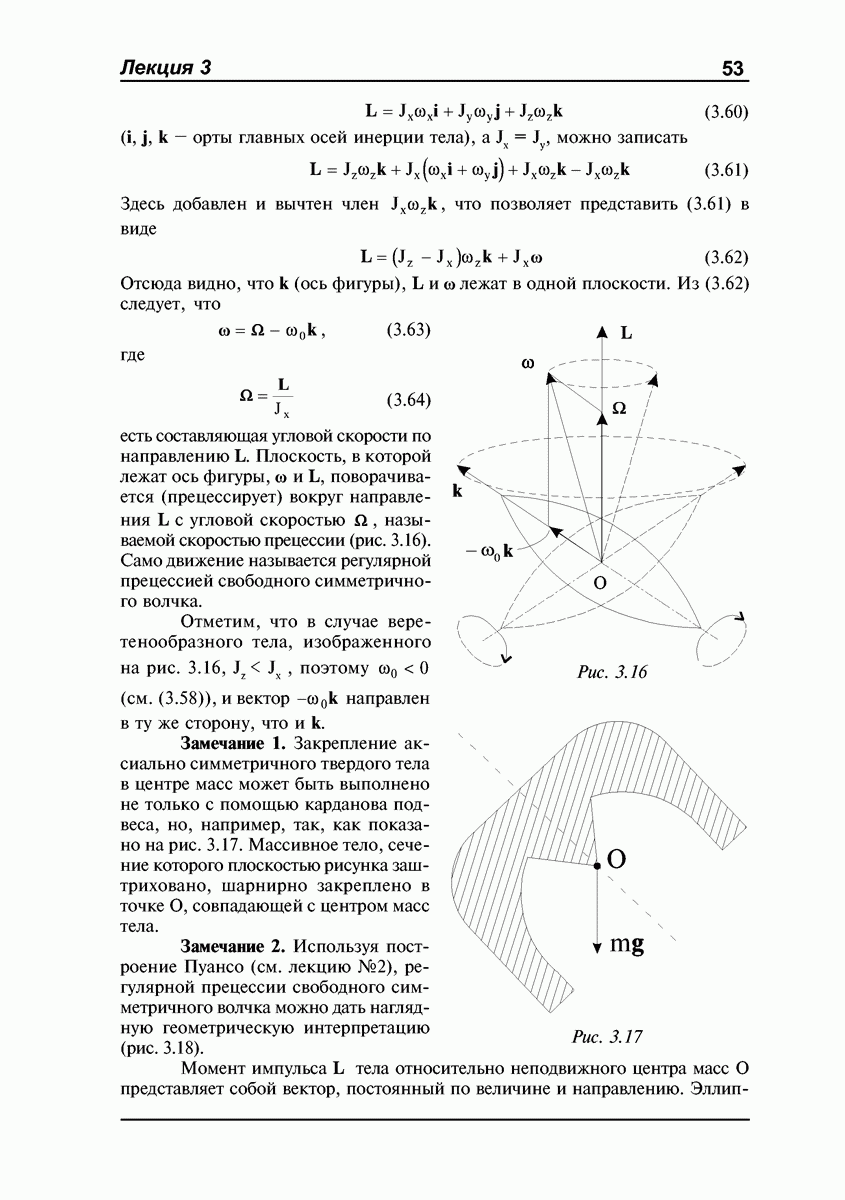
- Эллипсоид инерции.
- Вычисление моментов инерции относительно оси.
- Теорема Гюйгенса-Штейнера.
- Момент импульса тела относительно движущегося центра масс.
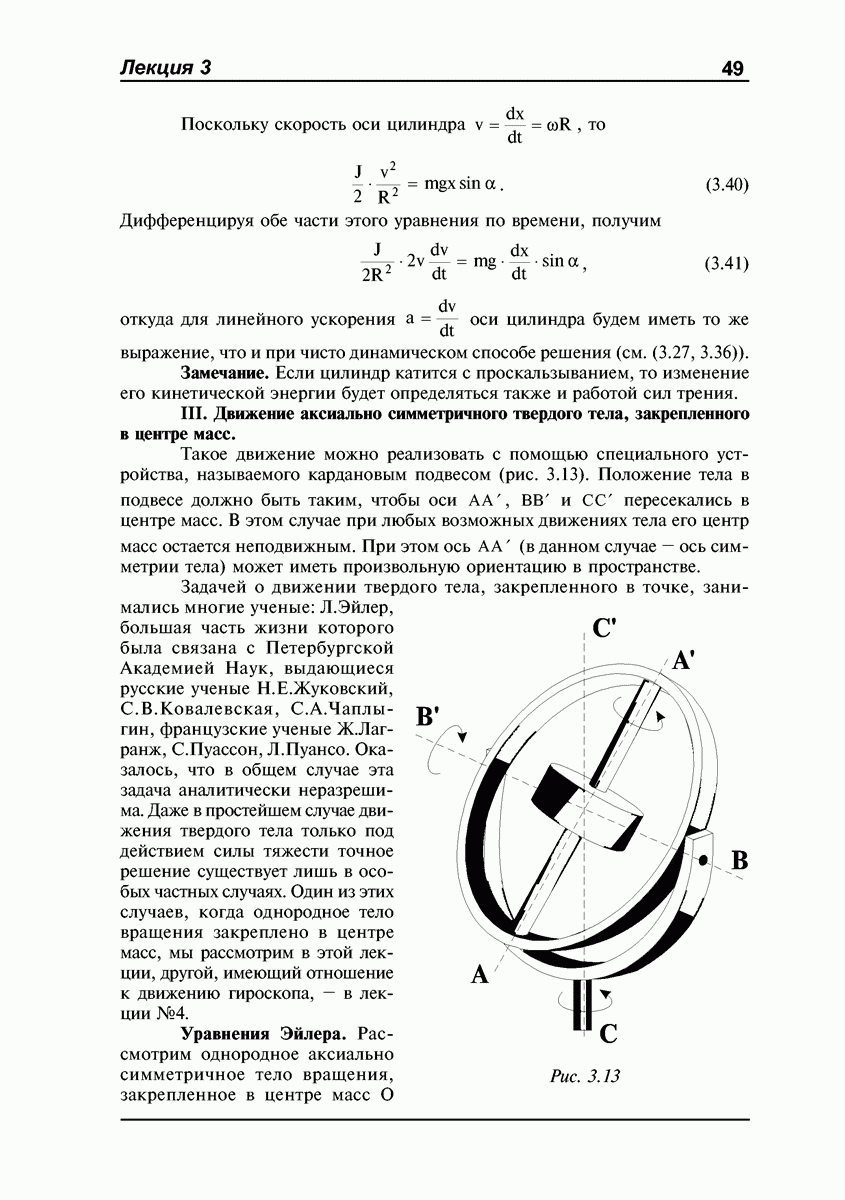
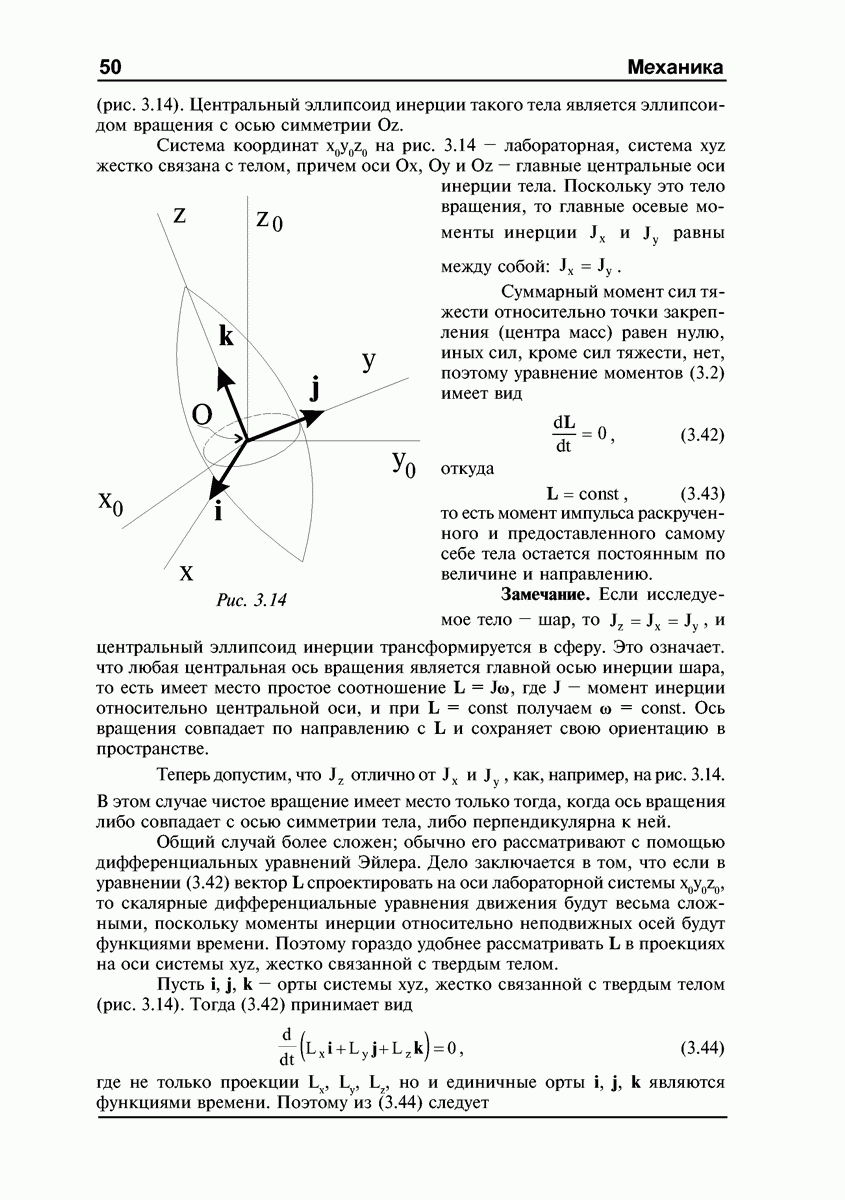
- ЛЕКЦИЯ №3. Динамика абсолютно твердого тела. Уравнение поступательного движения и уравнение моментов. Вращение твердого тела вокруг неподвижной оси. Центр удара. Динамика плоского движения твердого тела. Движение аксиально симметричного твердого тела, закрепленного в центре масс. Уравнения Эйлера.
- Уравнения динамики твердого тела. Общий случай.
- Кинетическая энергия вращающегося тела и работа внешних сил (ось вращения неподвижна).
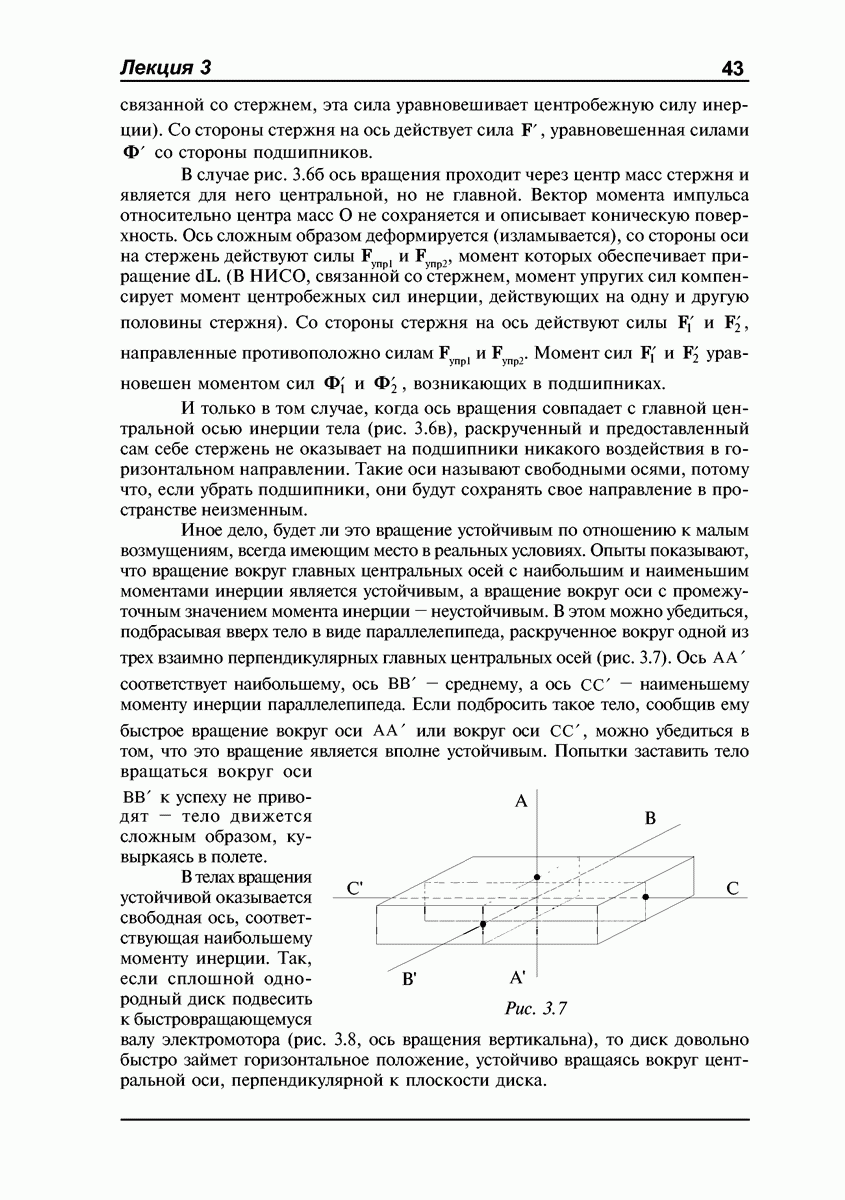
- Свободные оси. Устойчивость свободного вращения.
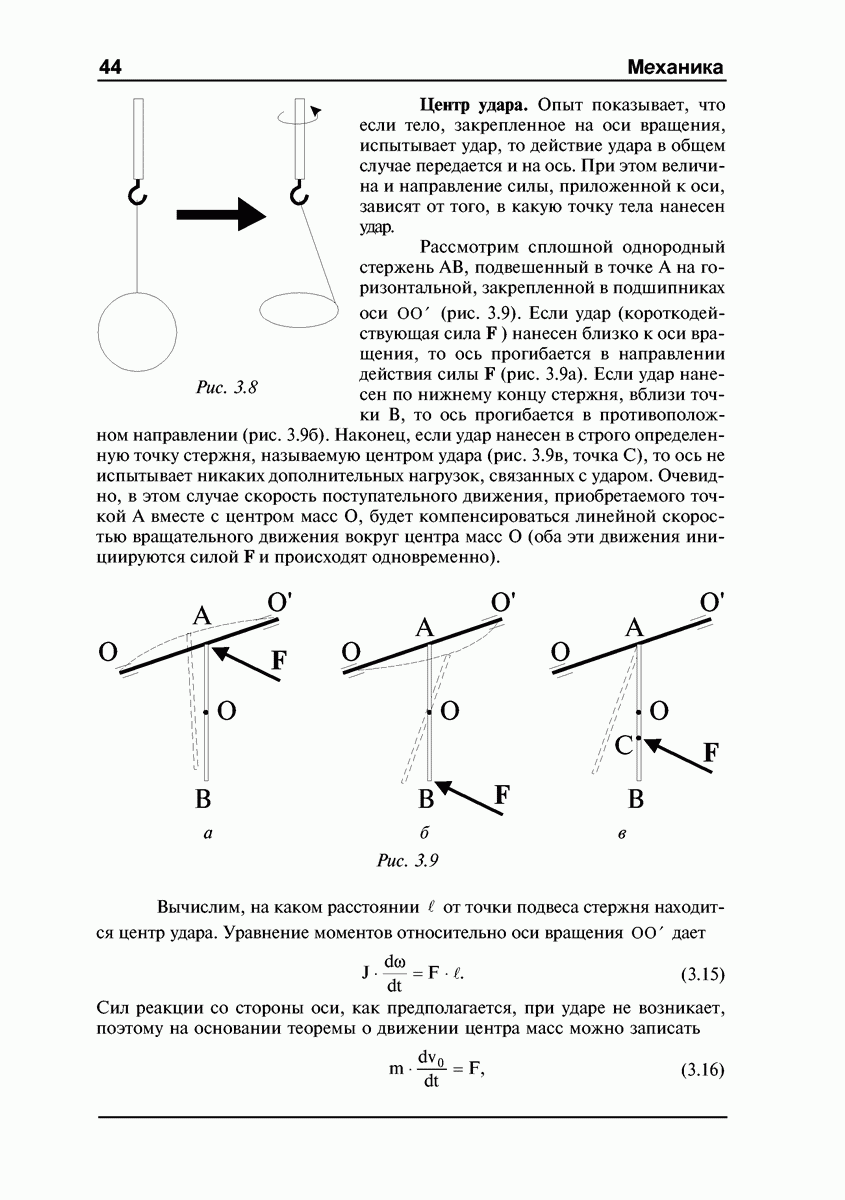
- Центр удара.
- Кинетическая энергия при плоском движении.
- Уравнения Эйлера.
- ЛЕКЦИЯ №4. Гироскопы. Свободный гироскоп. Прецессия гироскопа под действием внешних сил. Угловая скорость прецессии. Нутации. Гироскопические силы, их природа и проявления.
- Свободный гироскоп.
- Прецессия гироскопа под действием внешних сил. Элементарная теория.
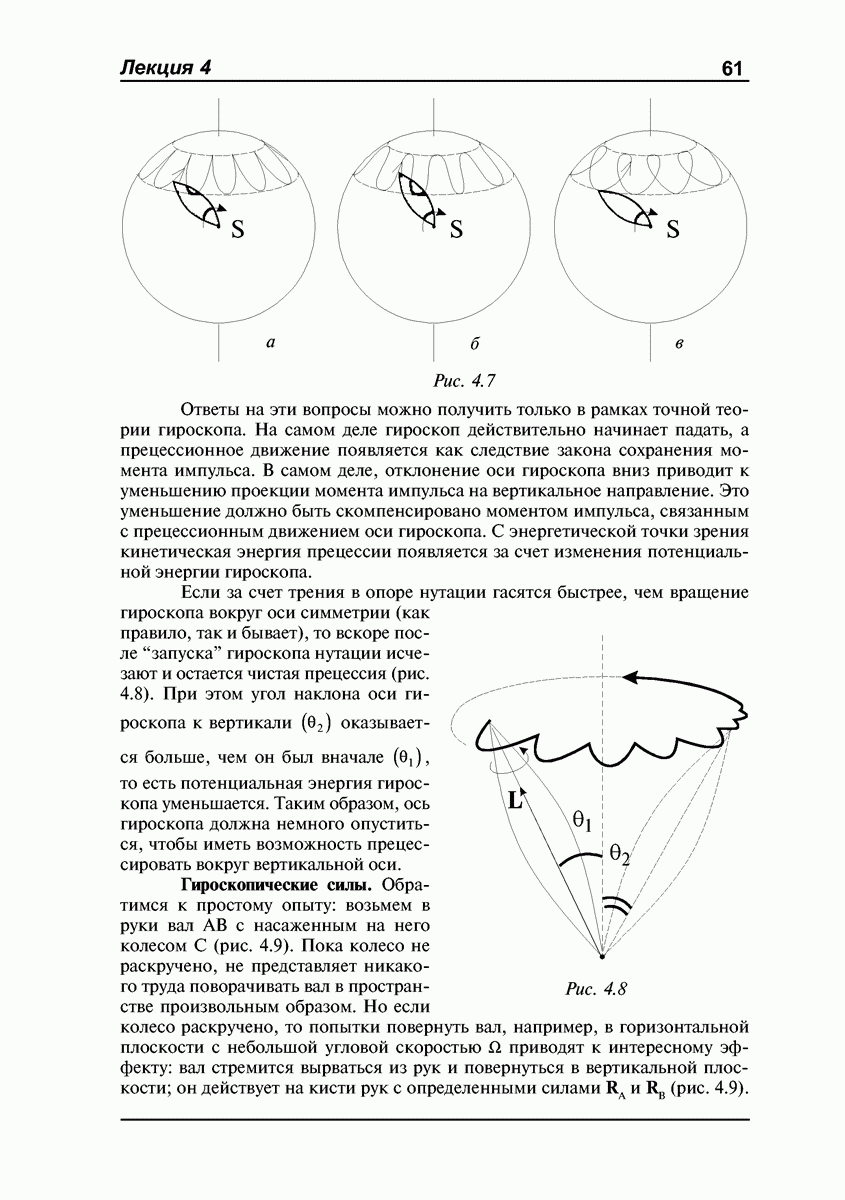
- Прецессия гироскопа под действием внешних сил. Отход от элементарной теории. Нутации.
- Гироскопические силы.
- Волчки.
- ЛИТЕРАТУРА