| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
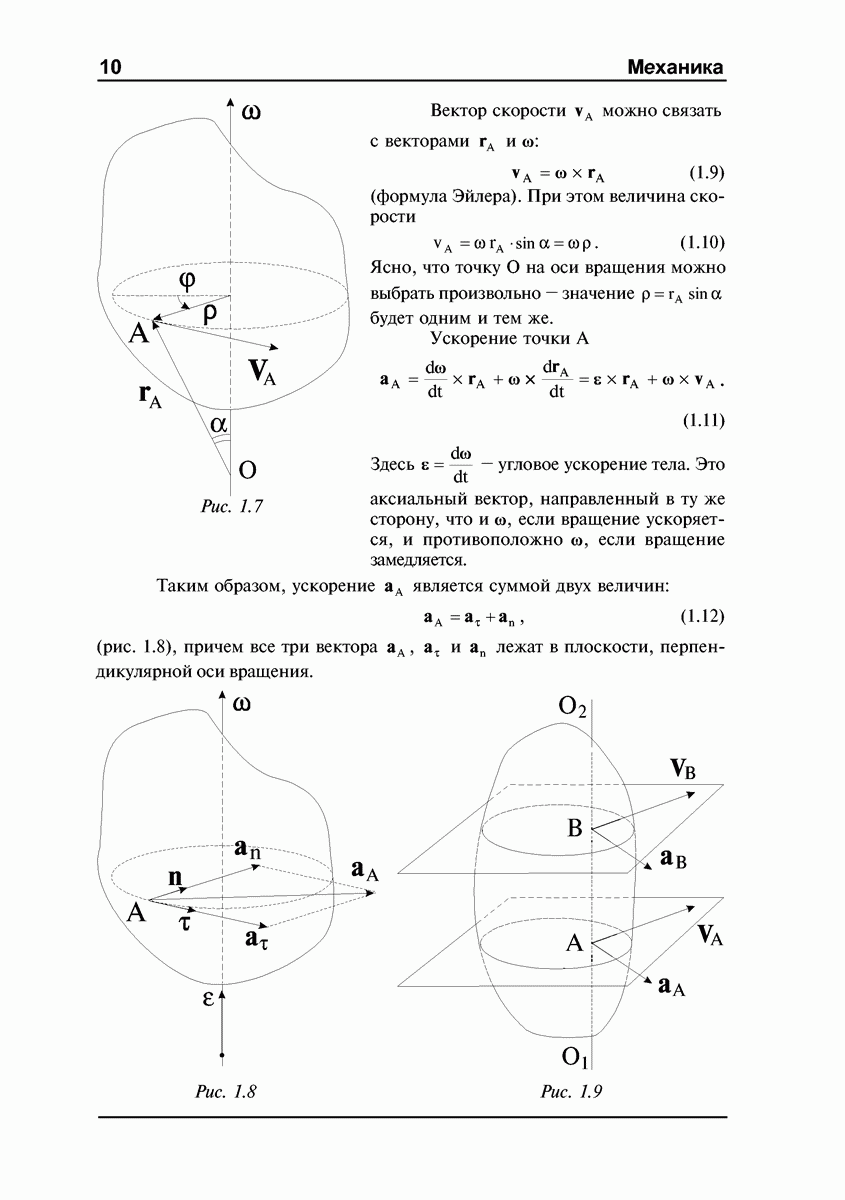
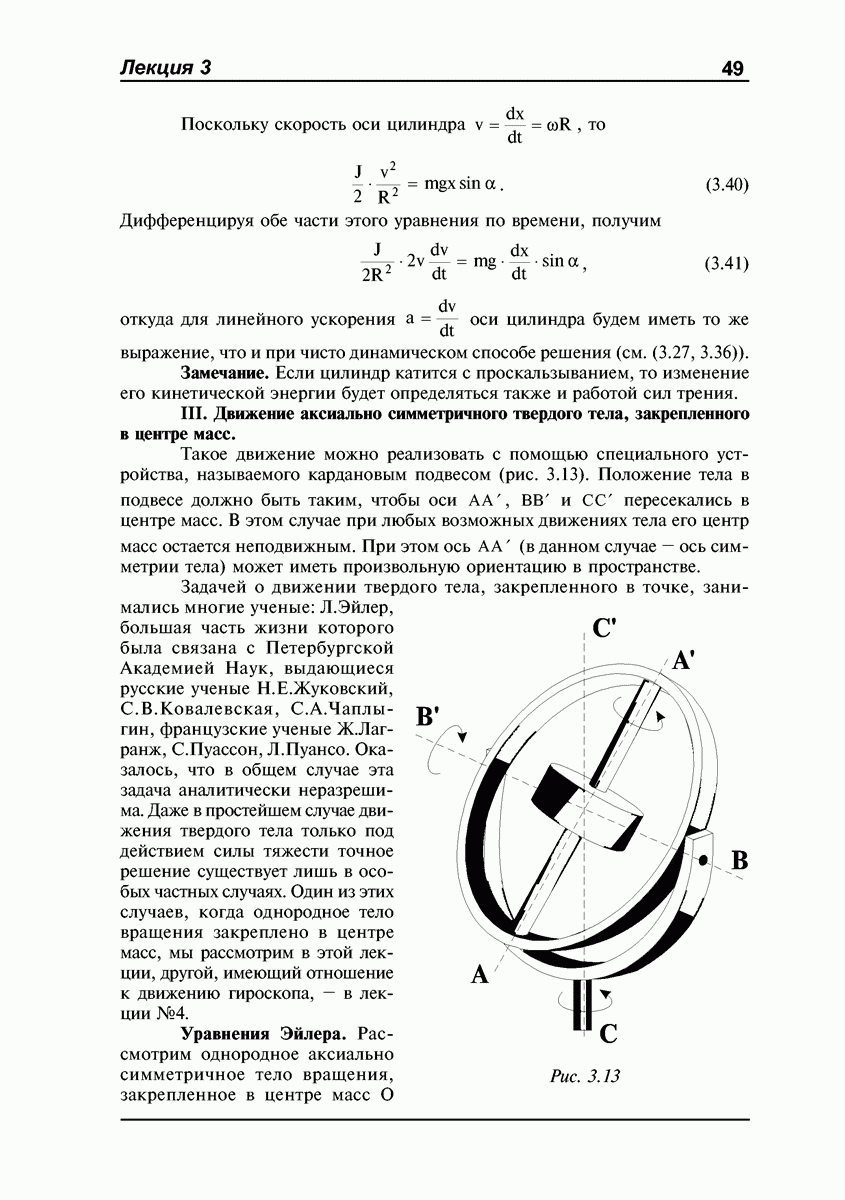
Движение твердого тела с одной неподвижной точкой.
Примеры таких тел показаны на рис. 1.20: волчок с шарнирно закрепленным острием  конус, катающийся по плоскости без проскальзывания (б). В этом случае тело имеет три степени свободы — начала систем
конус, катающийся по плоскости без проскальзывания (б). В этом случае тело имеет три степени свободы — начала систем  и
и  введенных в начале лекции, можно совместить с точкой закрепления, а для описания движения тела использовать три угла Эйлера:
введенных в начале лекции, можно совместить с точкой закрепления, а для описания движения тела использовать три угла Эйлера:

Для твердого тела с одной неподвижной точкой справедлива теорема Эйлера: твердое тело, закрепленное в одной точке, может быть переведено

Рис. 1.20
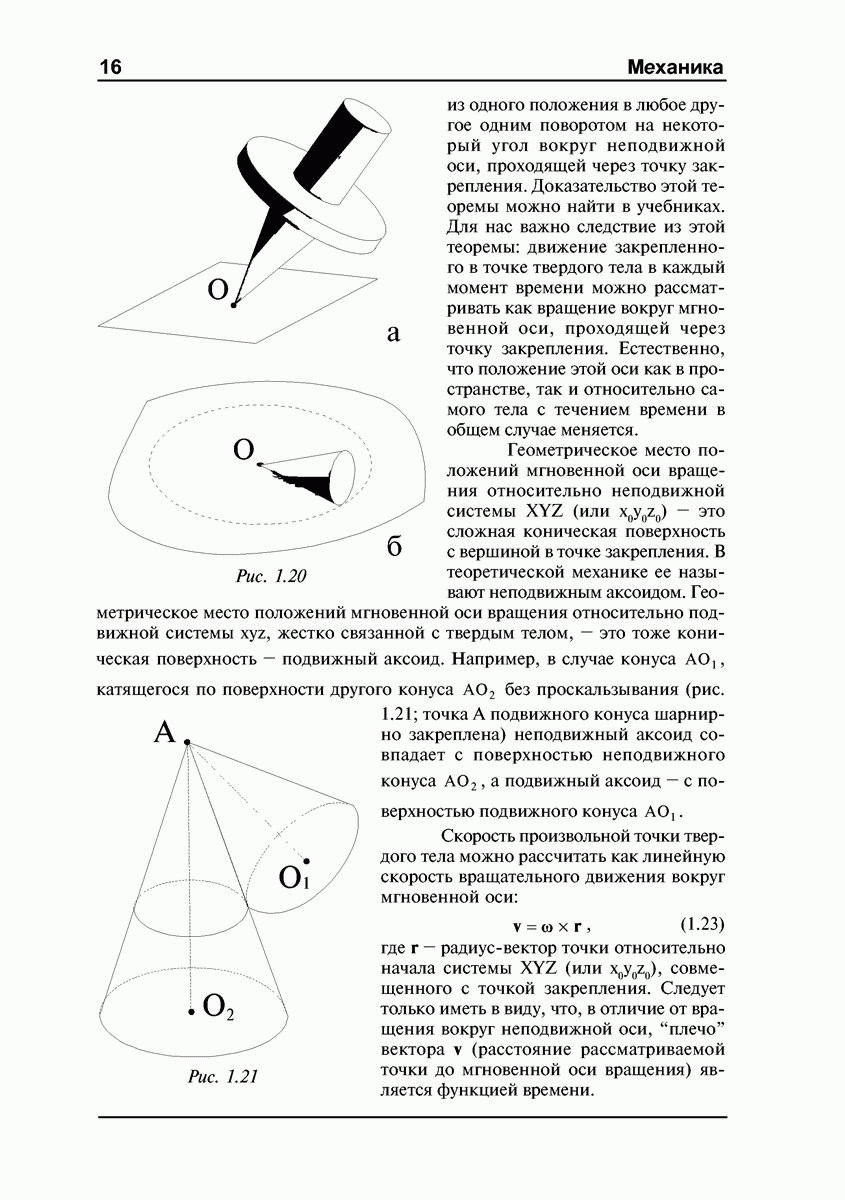
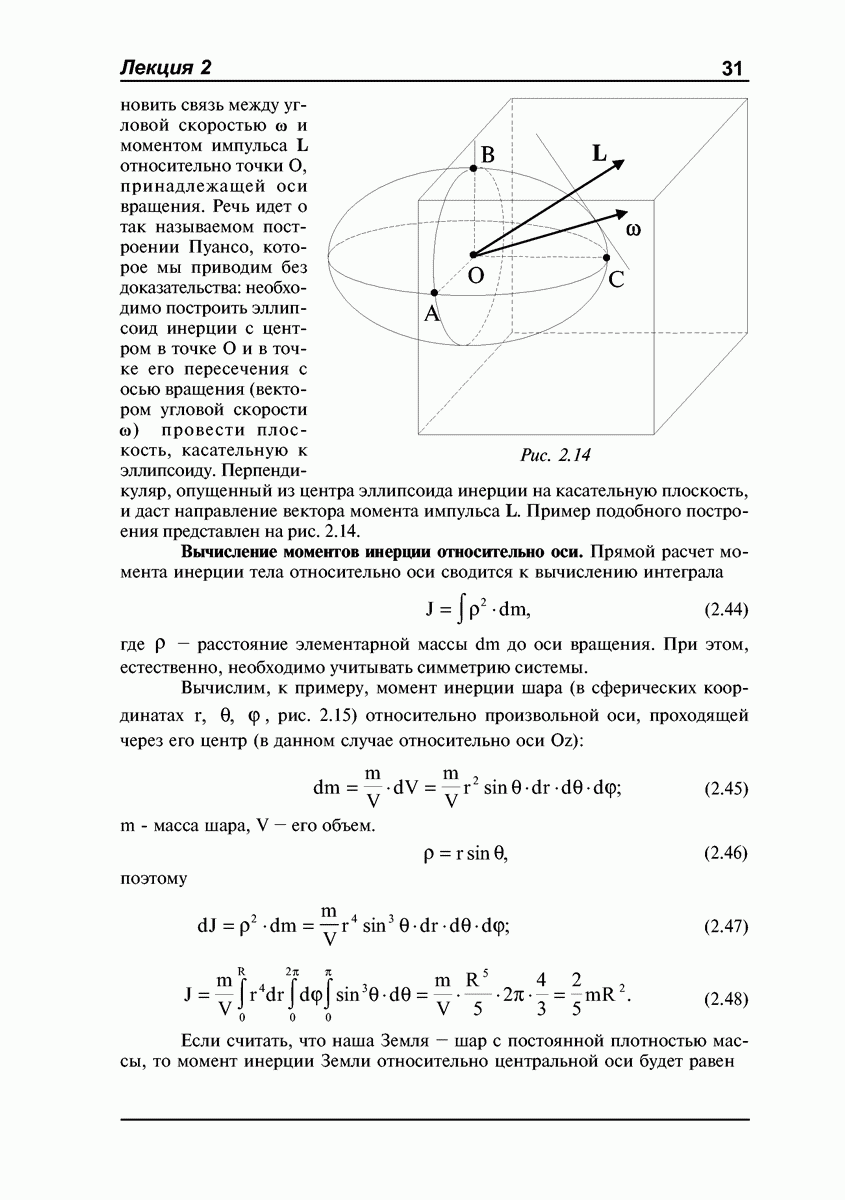
из одного положения в любое другое одним поворотом на некоторый угол вокруг неподвижной оси, проходящей через точку закрепления. Доказательство этой теоремы можно найти в учебниках. Для нас важно следствие из этой теоремы: движение закрепленного в точке твердого тела в каждый момент времени можно рассматривать как вращение вокруг мгновенной оси, проходящей через точку закрепления. Естественно, что положение этой оси как в пространстве, так и относительно самого тела с течением времени в общем случае меняется.
Геометрическое место положений мгновенной оси вращения относительно неподвижной системы  (или
(или  ) — это сложная коническая поверхность с вершиной в точке закрепления. В теоретической механике ее называют неподвижным аксоидом. Геометрическое место положений мгновенной оси вращения относительно подвижной системы
) — это сложная коническая поверхность с вершиной в точке закрепления. В теоретической механике ее называют неподвижным аксоидом. Геометрическое место положений мгновенной оси вращения относительно подвижной системы  жестко связанной с твердым телом, — это тоже коническая поверхность — подвижный аксоид. Например, в случае конуса
жестко связанной с твердым телом, — это тоже коническая поверхность — подвижный аксоид. Например, в случае конуса  катящегося по поверхности другого конуса
катящегося по поверхности другого конуса  без проскальзывания (рис. 1.21; точка А подвижного конуса шарнирно закреплена) неподвижный аксоид совпадает с поверхностью неподвижного конуса
без проскальзывания (рис. 1.21; точка А подвижного конуса шарнирно закреплена) неподвижный аксоид совпадает с поверхностью неподвижного конуса  а подвижный аксоид — с поверхностью подвижного конуса
а подвижный аксоид — с поверхностью подвижного конуса 
Скорость произвольной точки твердого тела можно рассчитать как линейную скорость вращательного движения вокруг мгновенной оси:

где  — радиус-вектор точки относительно начала системы
— радиус-вектор точки относительно начала системы  (или
(или  совмещенного с точкой закрепления. Следует только иметь в виду, что, в отличие от вращения вокруг неподвижной оси, “плечо” вектора
совмещенного с точкой закрепления. Следует только иметь в виду, что, в отличие от вращения вокруг неподвижной оси, “плечо” вектора  (расстояние рассматриваемой точки до мгновенной оси вращения) является функцией времени.
(расстояние рассматриваемой точки до мгновенной оси вращения) является функцией времени.

Рис. 1.21
Ускорение произвольной точки твердого тела

состоит из двух частей: ускорения, связанного с неравномерностью вращения (изменением о по величине и направлению)

и центростремительного (нормального) ускорения

где  — радиус-вектор, проведенный от мгновенной оси вращения в рассматриваемую точку. Здесь следует помнить, что угловое ускорение
— радиус-вектор, проведенный от мгновенной оси вращения в рассматриваемую точку. Здесь следует помнить, что угловое ускорение  связано с изменением угловой скорости не только по величине, но и по направлению, так что
связано с изменением угловой скорости не только по величине, но и по направлению, так что  не перпендикулярны друг другу.
не перпендикулярны друг другу.
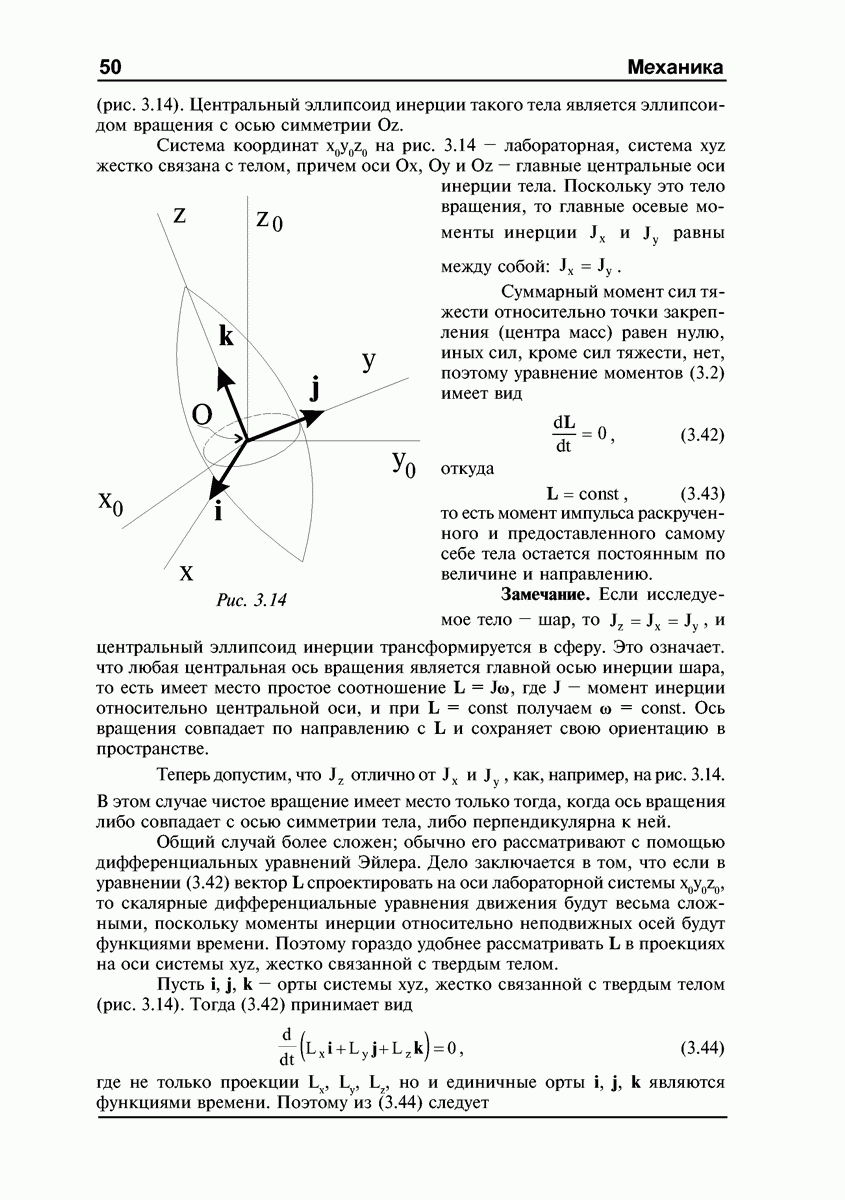
Проекции вектора мгновенной угловой скорости о на оси системы  жестко связанной с твердым телом, можно выразить через углы Эйлера
жестко связанной с твердым телом, можно выразить через углы Эйлера  (см. рис. 1.3) и их производные по времени
(см. рис. 1.3) и их производные по времени  Действительно, вектор
Действительно, вектор  можно представить в виде суммы трех составляющих:
можно представить в виде суммы трех составляющих:

Здесь  — единичные векторы вдоль осей
— единичные векторы вдоль осей  соответственно,
соответственно,  — единичный вектор вдоль линии узлов
— единичный вектор вдоль линии узлов  (на рис. 1.3 эти орты не показаны). Определим проекции векторов
(на рис. 1.3 эти орты не показаны). Определим проекции векторов  входящих в (1.27), на оси системы
входящих в (1.27), на оси системы  (см. рис. 1.3):
(см. рис. 1.3):

Из (1.27 - 1.30) получим:

Уравнения  называются кинематическими уравнениями Эйлера. Они, в частности, позволяют определить величину и направление вектора мгновенной угловой скорости со, если закон движения тела задан в виде (1.22).
называются кинематическими уравнениями Эйлера. Они, в частности, позволяют определить величину и направление вектора мгновенной угловой скорости со, если закон движения тела задан в виде (1.22).

Рис. 1.22
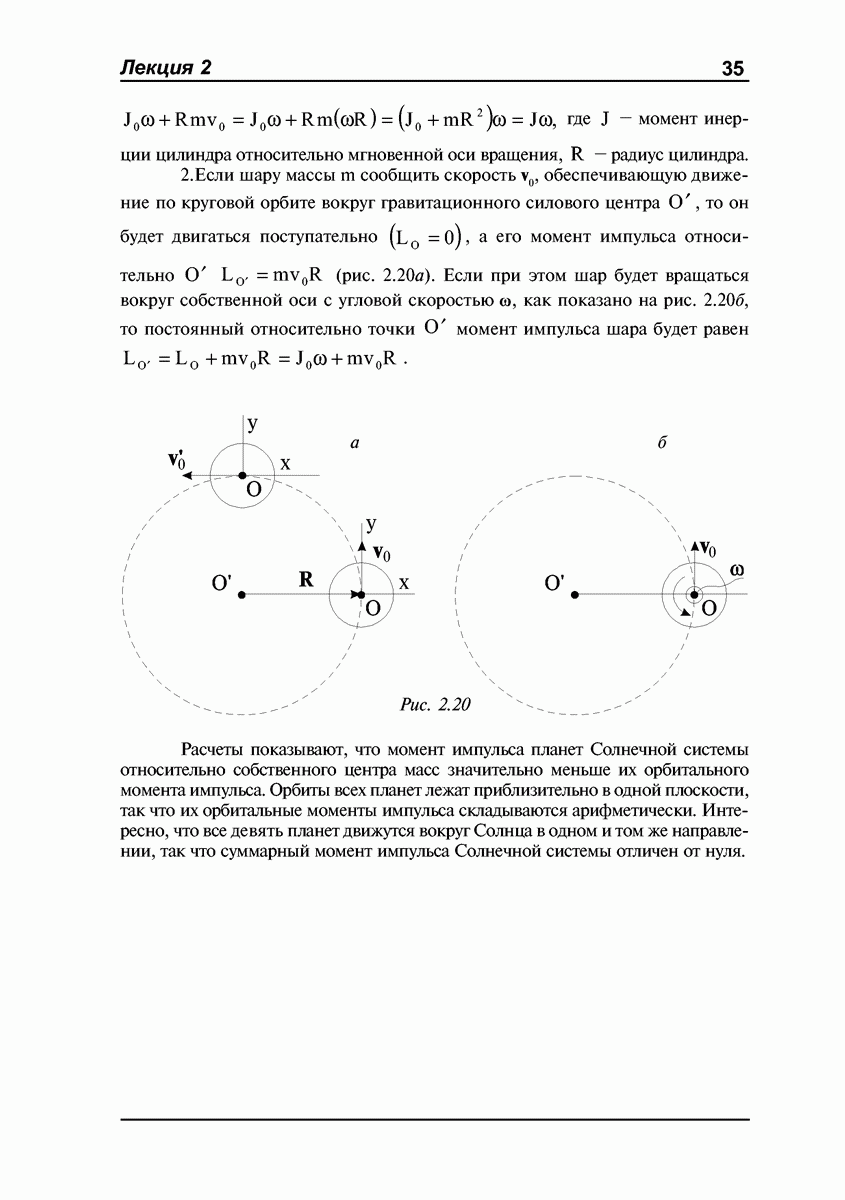
В ряде случаев вращение тела с закрепленной точкой вокруг мгновенной оси удобно представить как суперпозицию двух вращений вокруг пересекающихся осей. В случае, изображенном на рис. 1.22, вершина конуса шарнирно закреплена в точке О; ось конуса горизонтальна, а основание конуса катится без проскальзывания по горизонтальной плоскости  . Вектор угловой скорости со направлен вдоль мгновенной оси вращения
. Вектор угловой скорости со направлен вдоль мгновенной оси вращения  (скорость точек О и М равна нулю); при движении конуса мгновенная ось вращения изменяет свое положение, описывая некоторую коническую поверхность с вершиной в точке О. Абсолютное вращение конуса с угловой скоростью
(скорость точек О и М равна нулю); при движении конуса мгновенная ось вращения изменяет свое положение, описывая некоторую коническую поверхность с вершиной в точке О. Абсолютное вращение конуса с угловой скоростью  можно представить в виде суммы
можно представить в виде суммы

где  угловая скорость относительного вращения конуса вокруг собственной оси симметрии,
угловая скорость относительного вращения конуса вокруг собственной оси симметрии,  — угловая скорость переносного вращения самой оси конуса вокруг вертикали. Если задана
— угловая скорость переносного вращения самой оси конуса вокруг вертикали. Если задана  то
то

где  — угол полураствора конуса,
— угол полураствора конуса,  — радиус основания конуса,
— радиус основания конуса,  — его высота.
— его высота.
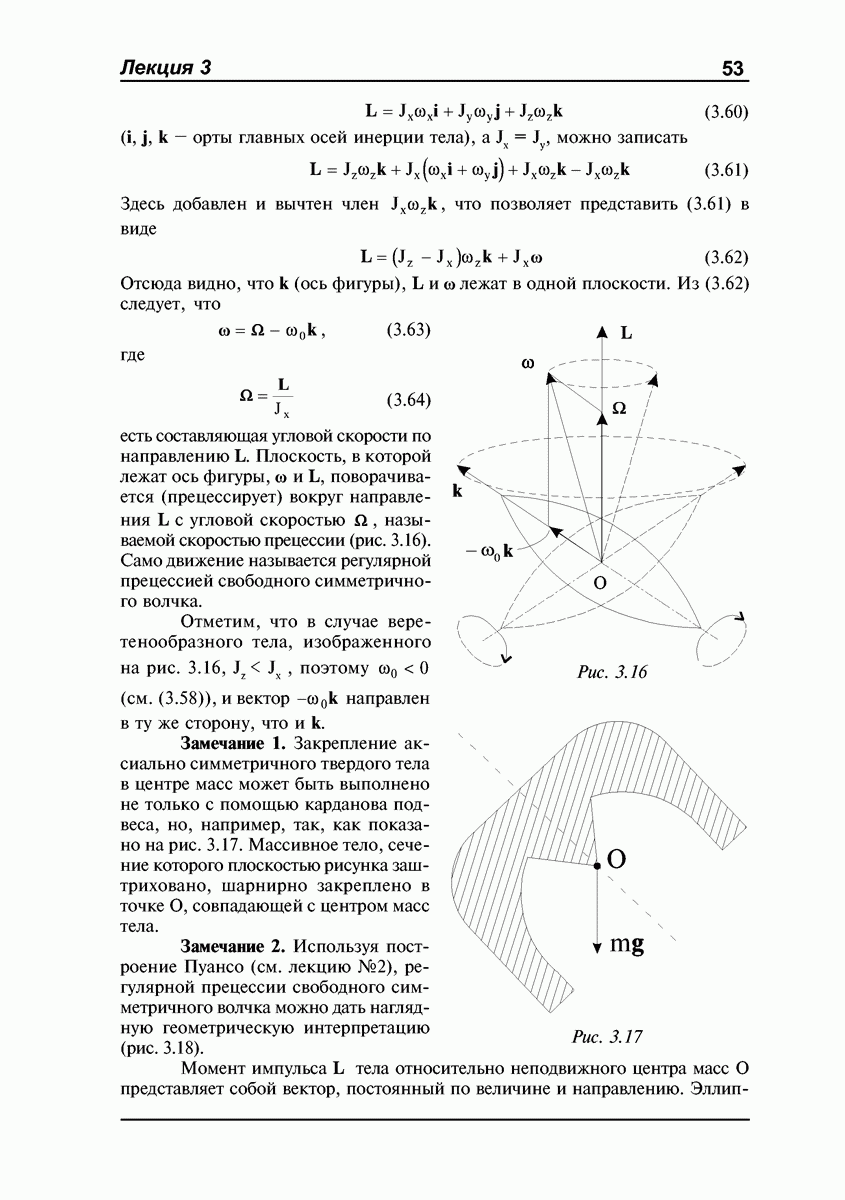
Замечание. Движение тела, представляющее собой одновременное вращение вокруг нескольких осей с угловыми скоростями сор  может быть сведено к вращению вокруг одной оси с угловой скоростью
может быть сведено к вращению вокруг одной оси с угловой скоростью

только в том случае, когда все оси вращения пересекаются в одной точке.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- ЛЕКЦИЯ №1. Кинематика абсолютно твердого тела. Степени свободы. Углы Эйлера. Поступательное движение. Вращение вокруг неподвижной оси. Плоское движение. Движение твердого тела, имеющего одну неподвижную точку. Движение свободного твердого тела.
- Поступательное движение
- Вращение вокруг неподвижной оси
- Плоское движение
- Движение твердого тела с одной неподвижной точкой.
- Движение свободного твердого тела.
- ЛЕКЦИЯ №2. Динамика абсолютно твердого тела. Момент импульса. Тензор инерции. Момент импульса тела относительно оси. Эллипсоид инерции. Вычисление моментов инерции относительно оси. Теорема Гюйгенса-Штейнера. Момент импульса относительно движущегося центра масс.
- Главные оси инерции.
- Момент импульса твердого тела относительно оси. Момент инерции относительно оси.
- Эллипсоид инерции.
- Вычисление моментов инерции относительно оси.
- Теорема Гюйгенса-Штейнера.
- Момент импульса тела относительно движущегося центра масс.
- ЛЕКЦИЯ №3. Динамика абсолютно твердого тела. Уравнение поступательного движения и уравнение моментов. Вращение твердого тела вокруг неподвижной оси. Центр удара. Динамика плоского движения твердого тела. Движение аксиально симметричного твердого тела, закрепленного в центре масс. Уравнения Эйлера.
- Уравнения динамики твердого тела. Общий случай.
- Кинетическая энергия вращающегося тела и работа внешних сил (ось вращения неподвижна).
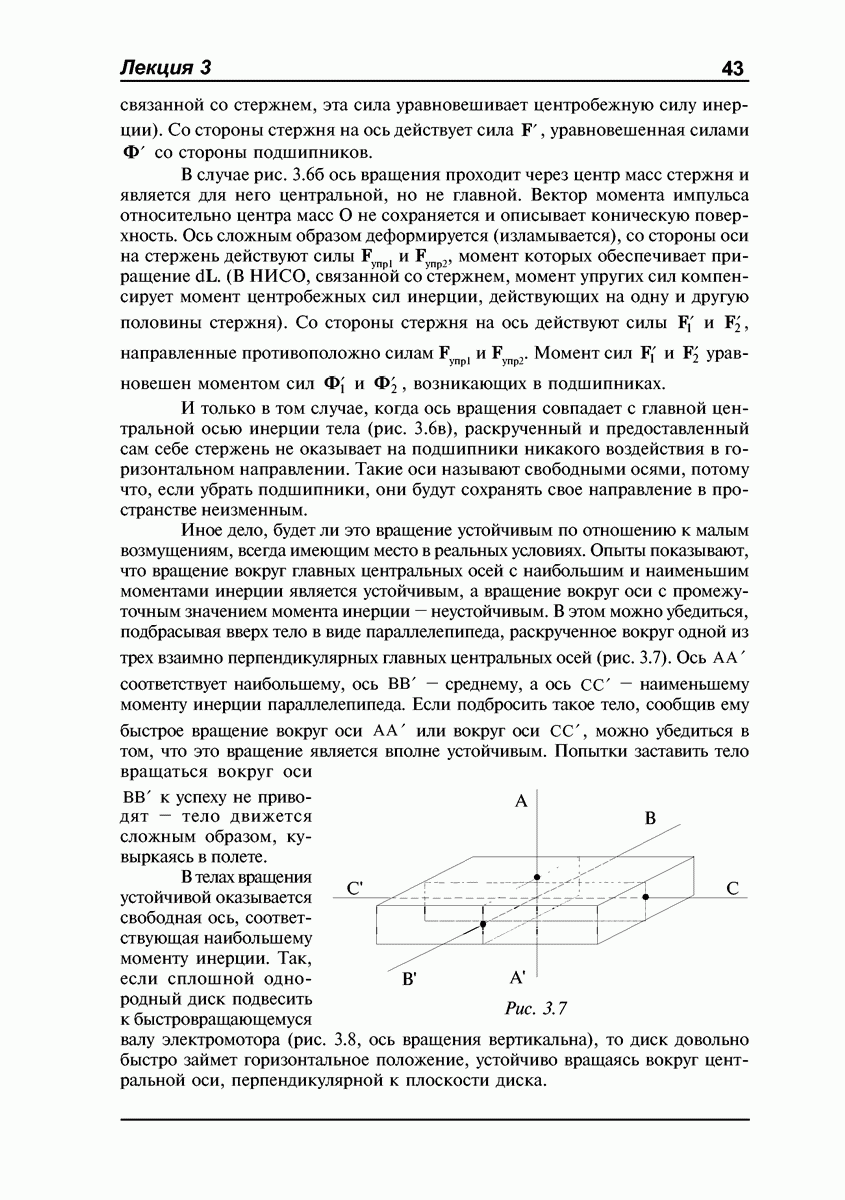
- Свободные оси. Устойчивость свободного вращения.
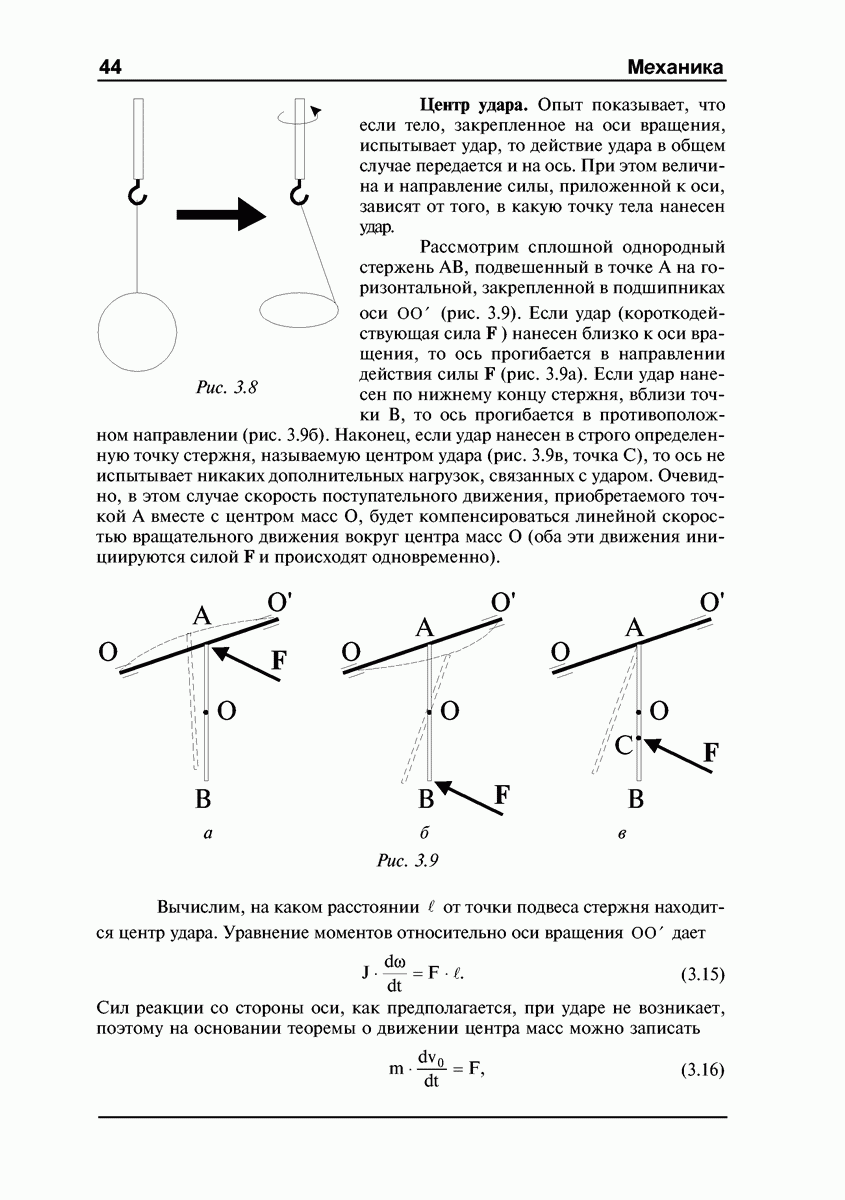
- Центр удара.
- Кинетическая энергия при плоском движении.
- Уравнения Эйлера.
- ЛЕКЦИЯ №4. Гироскопы. Свободный гироскоп. Прецессия гироскопа под действием внешних сил. Угловая скорость прецессии. Нутации. Гироскопические силы, их природа и проявления.
- Свободный гироскоп.
- Прецессия гироскопа под действием внешних сил. Элементарная теория.
- Прецессия гироскопа под действием внешних сил. Отход от элементарной теории. Нутации.
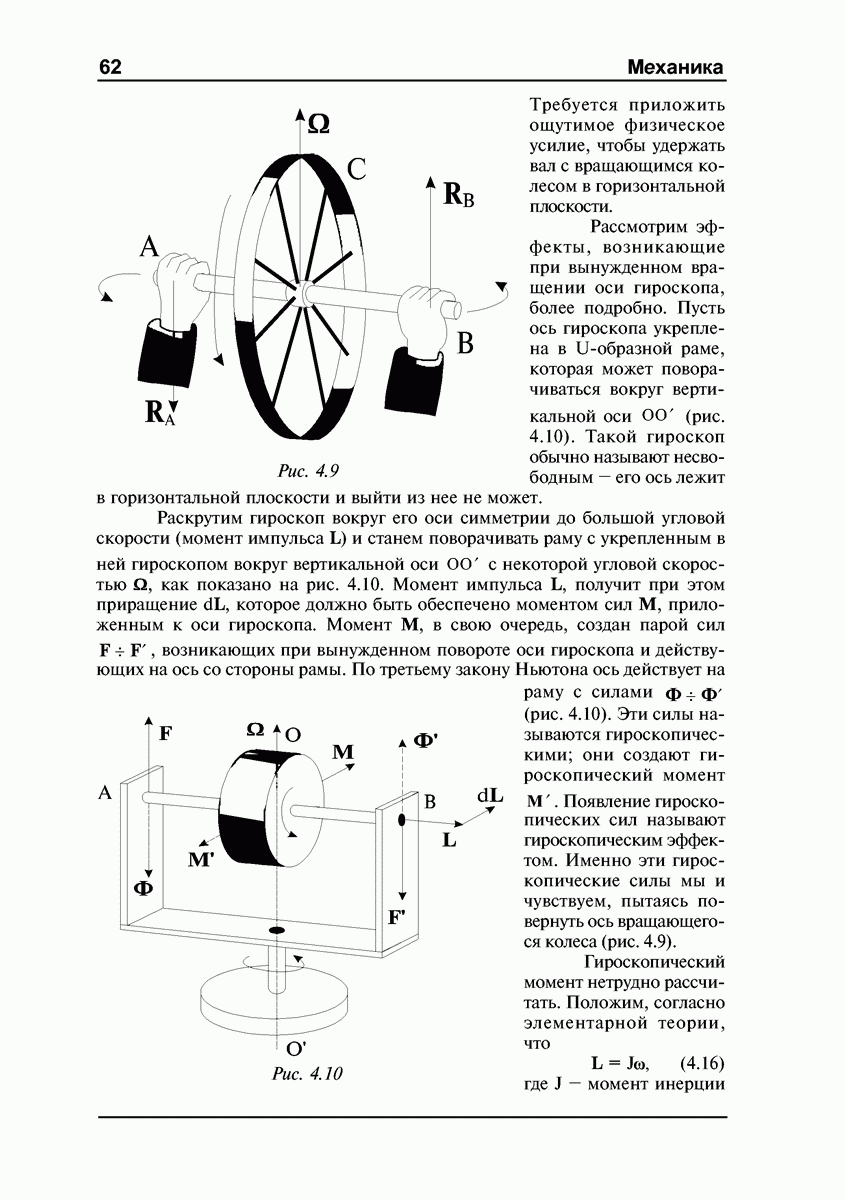
- Гироскопические силы.
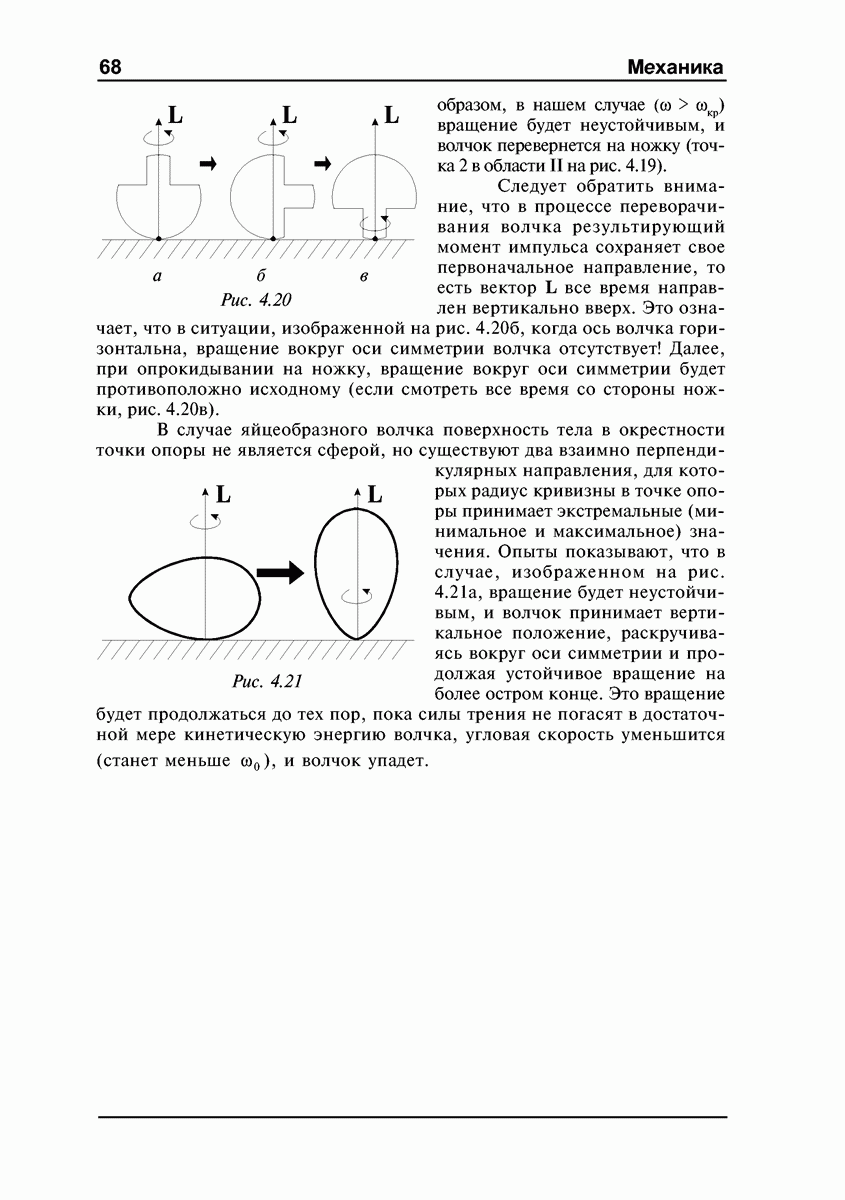
- Волчки.
- ЛИТЕРАТУРА