| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Гироскопические силы.
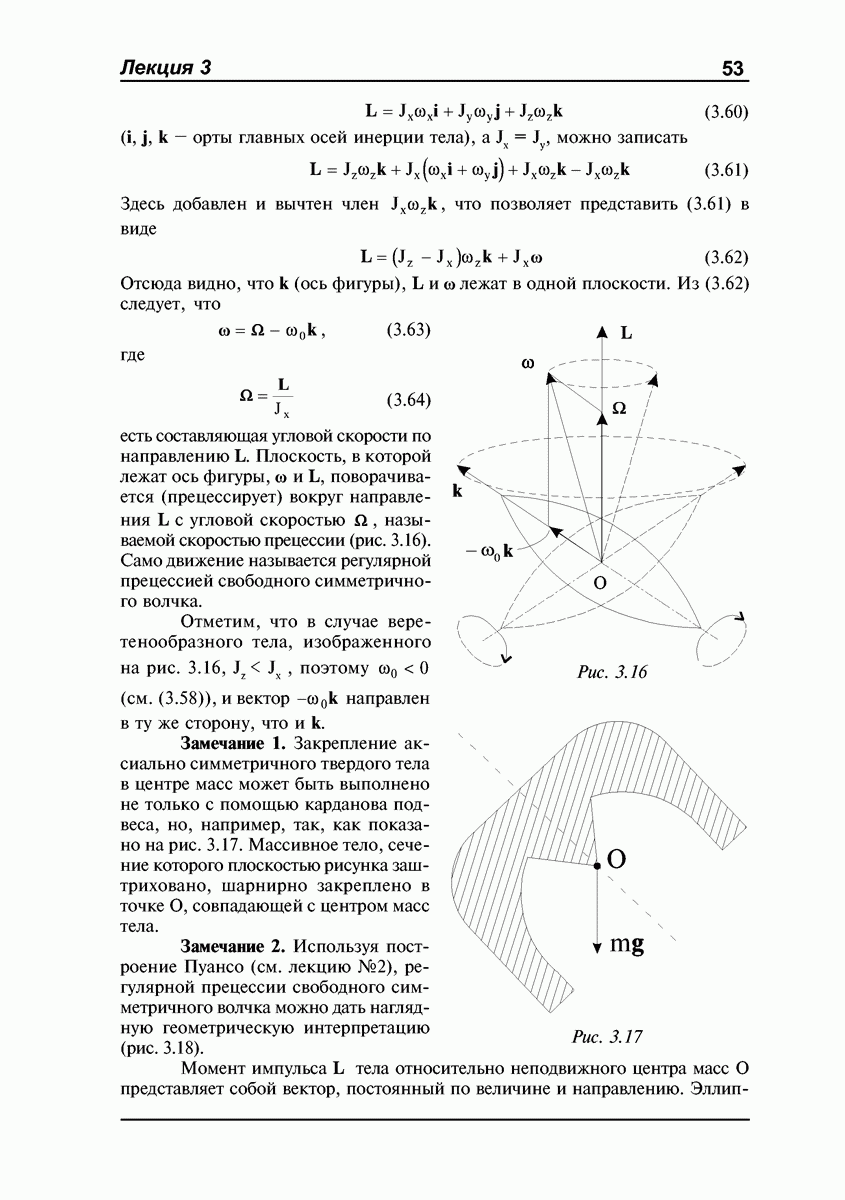
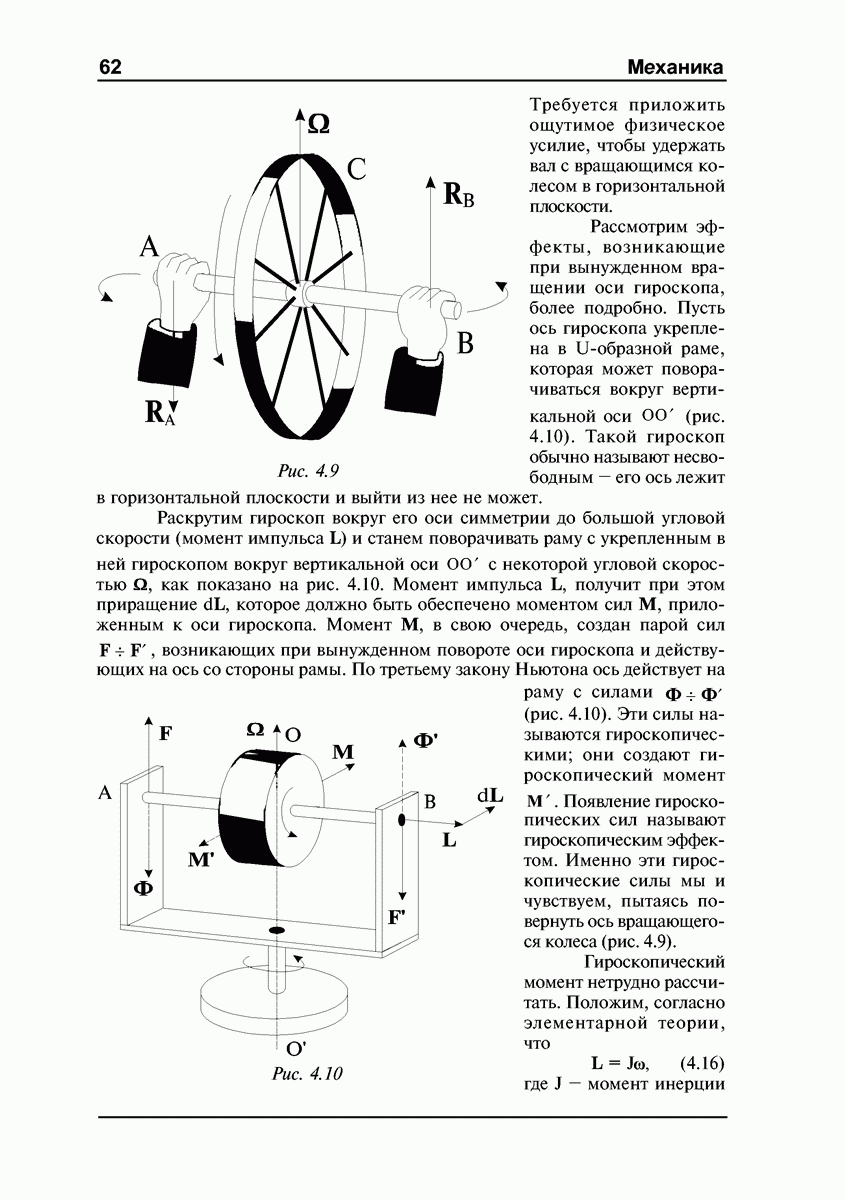
Обратимся к простому опыту: возьмем в руки вал  с насаженным на него колесом С (рис. 4.9). Пока колесо не раскручено, не представляет никакого труда поворачивать вал в пространстве произвольным образом. Но если колесо раскручено, то попытки повернуть вал, например, в горизонтальной плоскости с небольшой угловой скоростью О. приводят к интересному эффекту: вал стремится вырваться из рук и повернуться в вертикальной плоскости; он действует на кисти рук с определенными силами
с насаженным на него колесом С (рис. 4.9). Пока колесо не раскручено, не представляет никакого труда поворачивать вал в пространстве произвольным образом. Но если колесо раскручено, то попытки повернуть вал, например, в горизонтальной плоскости с небольшой угловой скоростью О. приводят к интересному эффекту: вал стремится вырваться из рук и повернуться в вертикальной плоскости; он действует на кисти рук с определенными силами  и
и  (рис. 4.9).
(рис. 4.9).

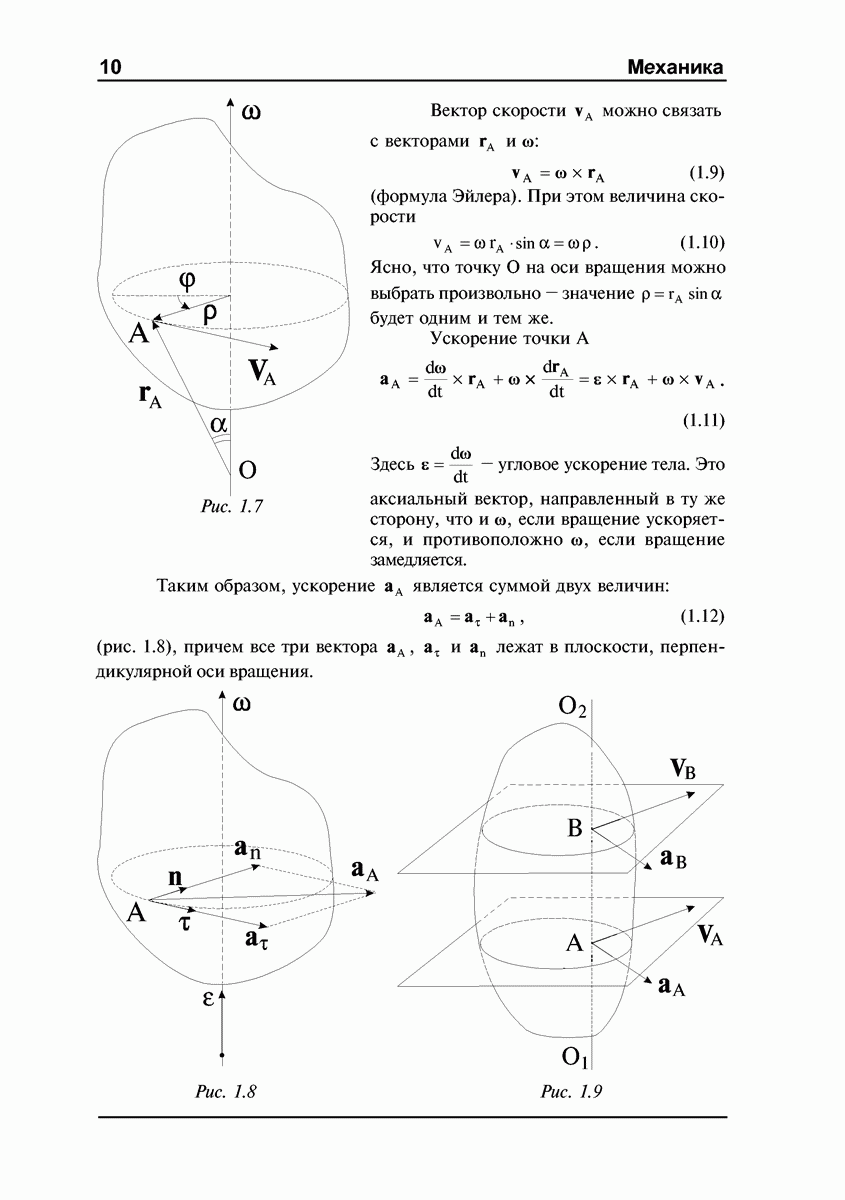
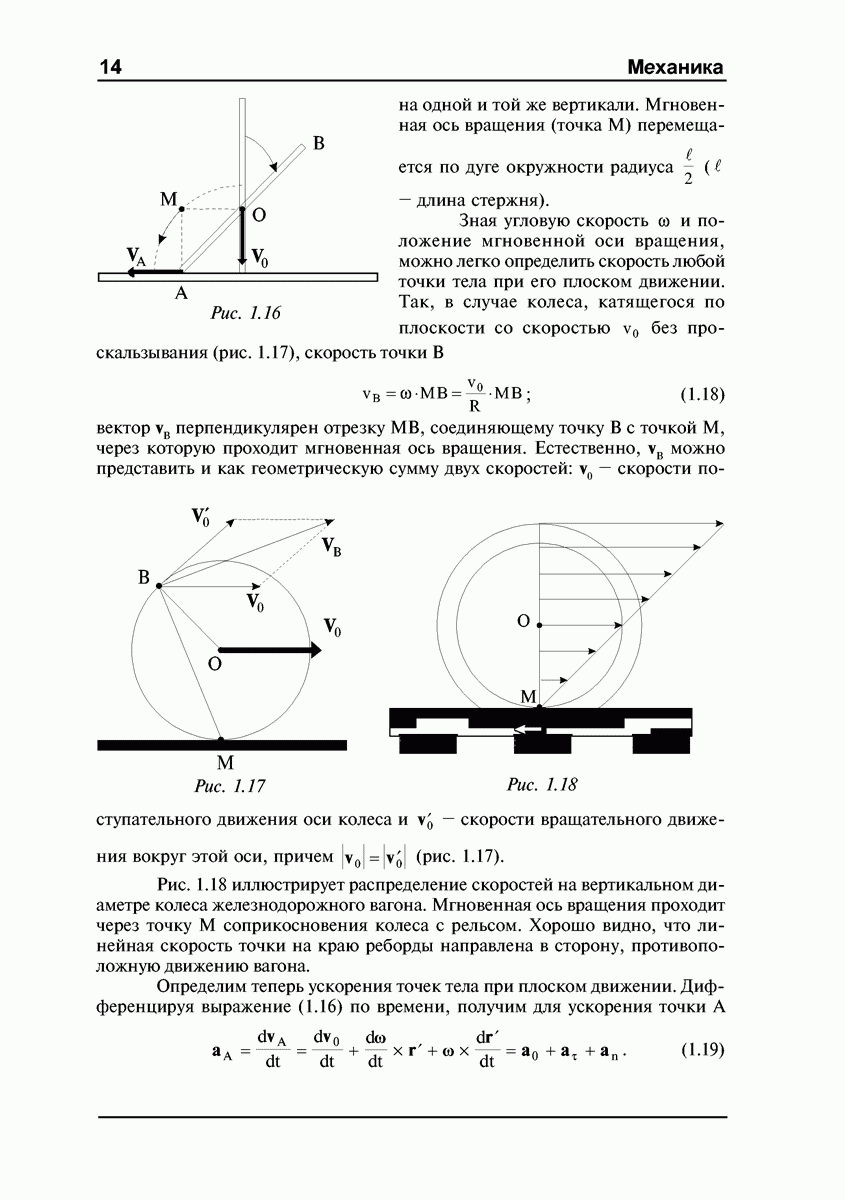
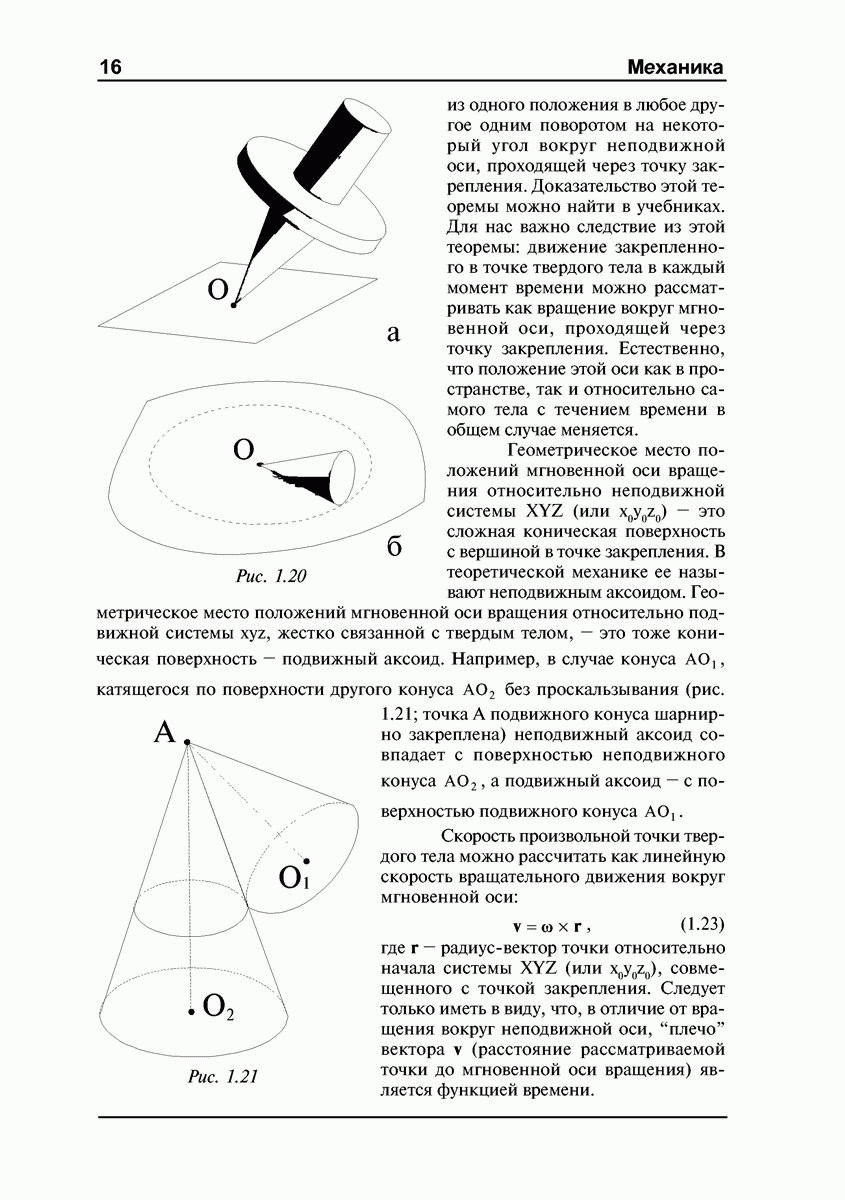
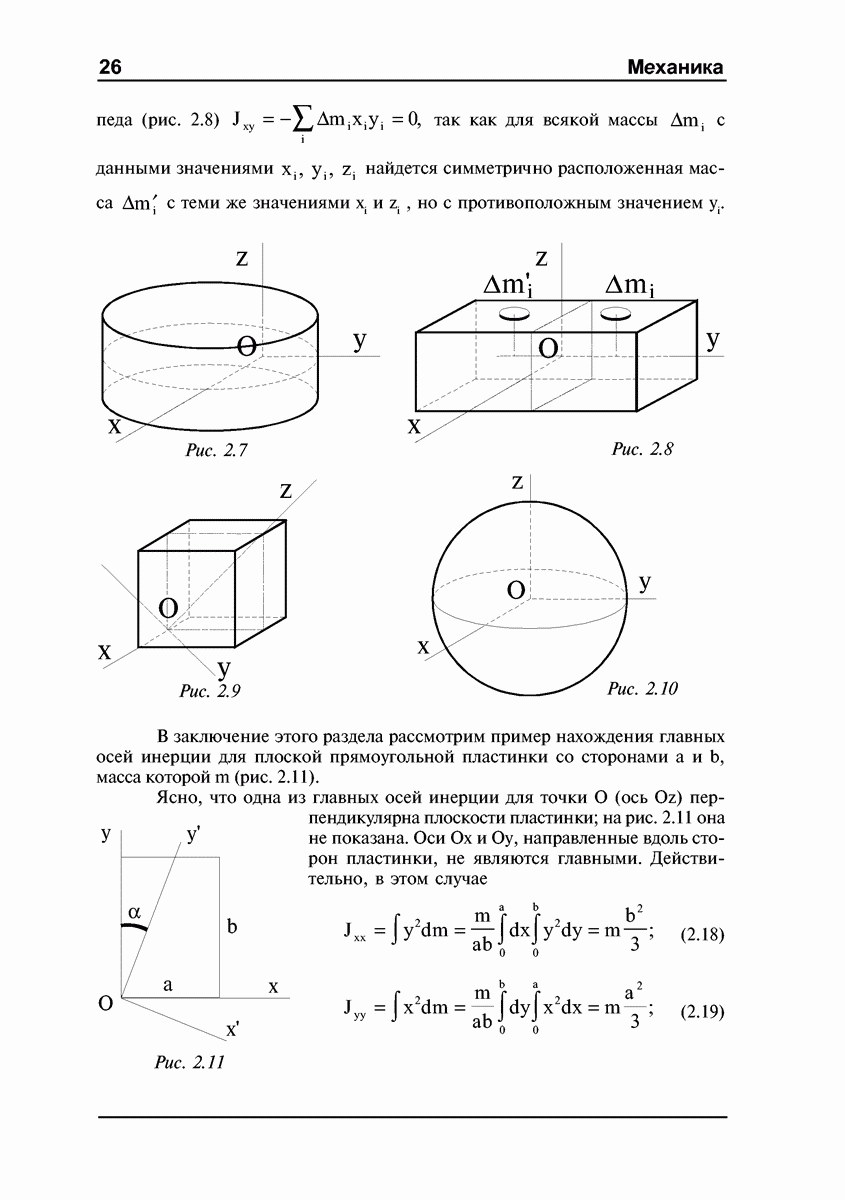
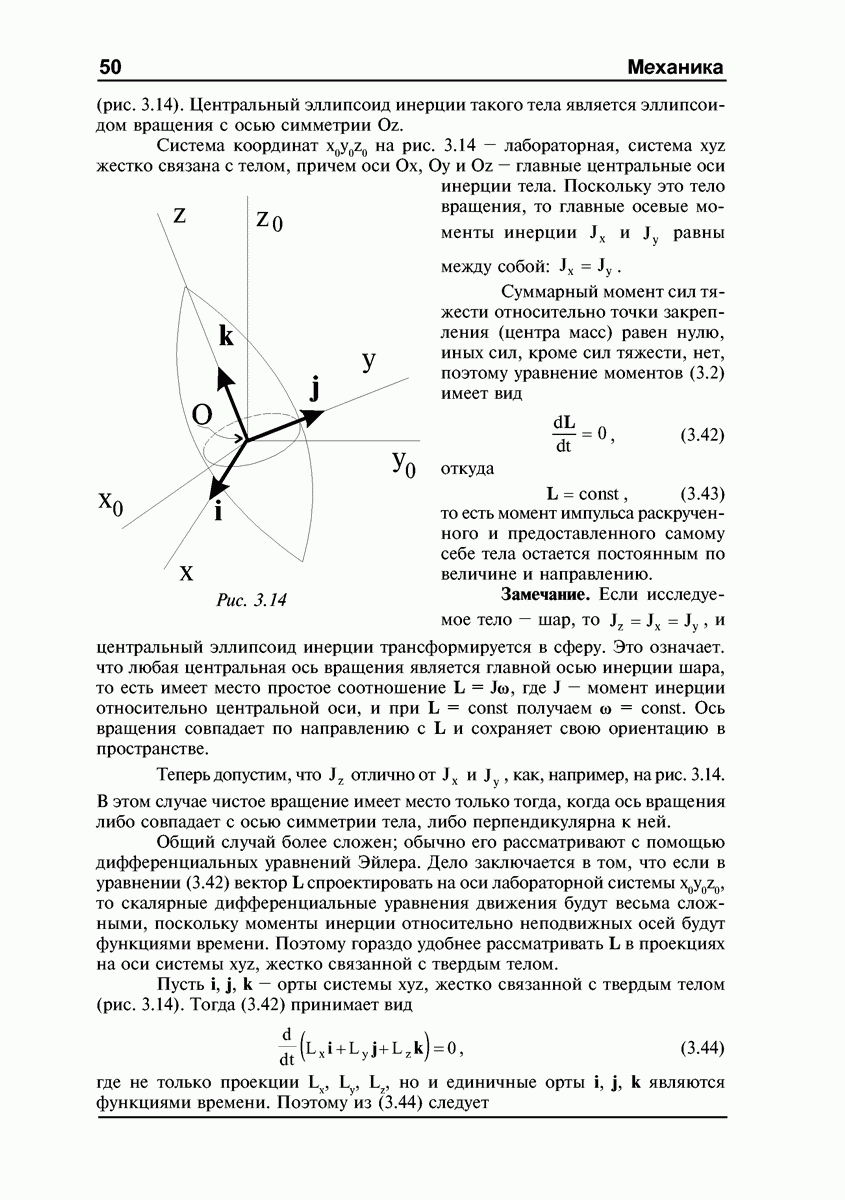
Рис. 4.8

Рис. 4.9
Требуется приложить ощутимое физическое усилие, чтобы удержать вал с вращающимся колесом в горизонтальной плоскости.
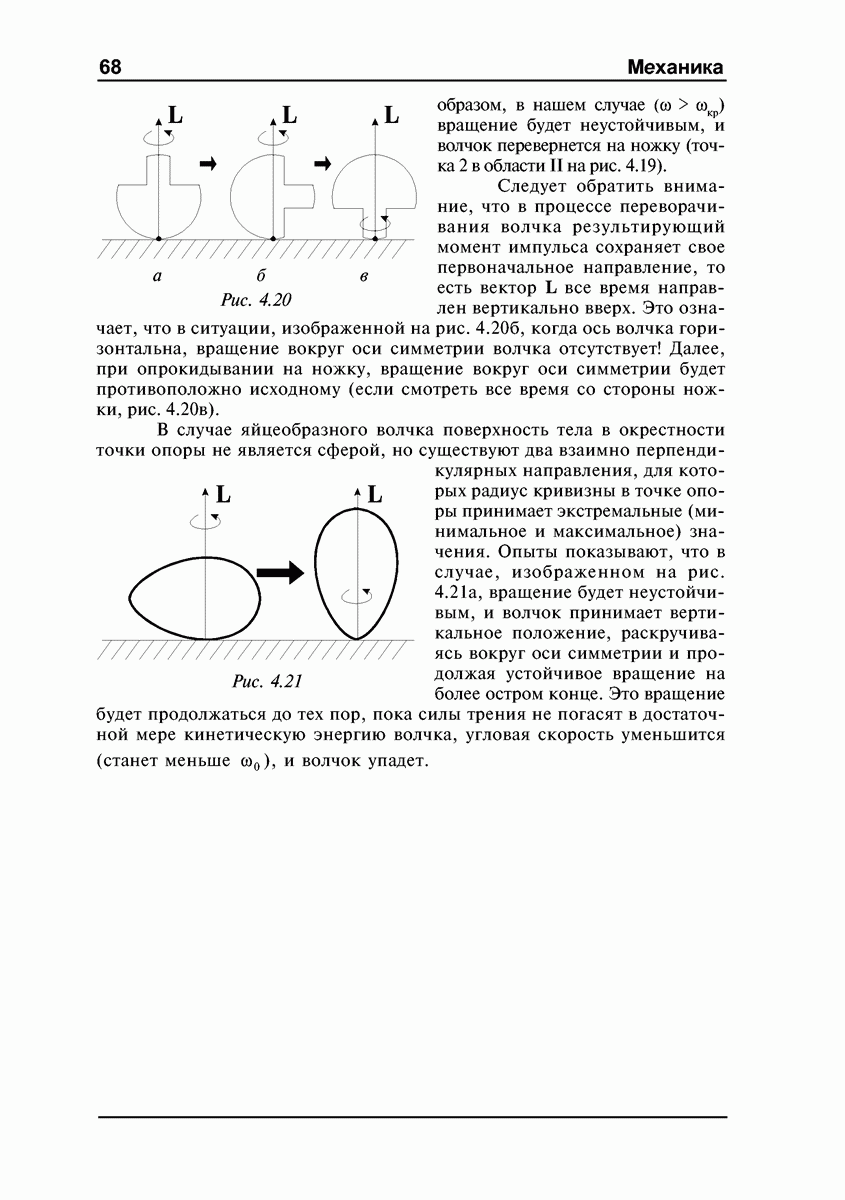
Рассмотрим эффекты, возникающие при вынужденном вращении оси гироскопа, более подробно. Пусть ось гироскопа укреплена в  -образной раме, которая может поворачиваться вокруг вертикальной оси
-образной раме, которая может поворачиваться вокруг вертикальной оси  (рис. 4.10). Такой гироскоп обычно называют несвободным — его ось лежит в горизонтальной плоскости и выйти из нее не может.
(рис. 4.10). Такой гироскоп обычно называют несвободным — его ось лежит в горизонтальной плоскости и выйти из нее не может.
Раскрутим гироскоп вокруг его оси симметрии до большой угловой скорости (момент импульса  и станем поворачивать раму с укрепленным в ней гироскопом вокруг вертикальной оси
и станем поворачивать раму с укрепленным в ней гироскопом вокруг вертикальной оси  с некоторой угловой скоростью
с некоторой угловой скоростью  как показано на рис. 4.10. Момент импульса
как показано на рис. 4.10. Момент импульса  получит при этом приращение
получит при этом приращение  которое должно быть обеспечено моментом сил М, приложенным к оси гироскопа. Момент М, в свою очередь, создан парой сил
которое должно быть обеспечено моментом сил М, приложенным к оси гироскопа. Момент М, в свою очередь, создан парой сил  возникающих при вынужденном повороте оси гироскопа и действующих на ось со стороны рамы. По третьему закону Ньютона ось действует на раму с силами
возникающих при вынужденном повороте оси гироскопа и действующих на ось со стороны рамы. По третьему закону Ньютона ось действует на раму с силами  (рис. 4.10). Эти силы называются гироскопическими; они создают гироскопический момент М. Появление гироскопических сил называют гироскопическим эффектом. Именно эти гироскопические силы мы и чувствуем, пытаясь повернуть ось вращающегося колеса (рис. 4.9).
(рис. 4.10). Эти силы называются гироскопическими; они создают гироскопический момент М. Появление гироскопических сил называют гироскопическим эффектом. Именно эти гироскопические силы мы и чувствуем, пытаясь повернуть ось вращающегося колеса (рис. 4.9).
Гироскопический момент нетрудно рассчитать. Положим, согласно элементарной теории, что

где  — момент инерции
— момент инерции

Рис. 4.10
гироскопа относительно его оси симметрии, а  угловая скорость собственного вращения. Тогда момент внешних сил, действующих на ось, будет равен
угловая скорость собственного вращения. Тогда момент внешних сил, действующих на ось, будет равен

где  — угловая скорость вынужденного поворота (иногда говорят: вынужденной прецессии). Со стороны оси на подшипники действует противоположный момент
— угловая скорость вынужденного поворота (иногда говорят: вынужденной прецессии). Со стороны оси на подшипники действует противоположный момент

Таким образом, вал гироскопа, изображенного на рис. 4.10, будет прижиматься кверху в подшипнике В и оказывать давление на нижнюю часть подшипника А.
Направление гироскопических сил можно легко найти с помощью правила, сформулированного Н.Е.Жуковским: гироскопические силы стремятся совместить момент импульса  гироскопа с направлением угловой скорости вынужденного поворота. Это правило можно наглядно продемонстрировать с помощью устройства, представленного на рис. 4.11.
гироскопа с направлением угловой скорости вынужденного поворота. Это правило можно наглядно продемонстрировать с помощью устройства, представленного на рис. 4.11.
Ось гироскопа закреплена в кольце, которое может свободно поворачиваться в обойме. Приведем обойму во вращение вокруг вертикальной оси с угловой скоростью  (вынужденный поворот), и кольцо с гироскопом будет поворачиваться в обойме до тех пор, пока направления
(вынужденный поворот), и кольцо с гироскопом будет поворачиваться в обойме до тех пор, пока направления  и
и  не совпадут. Такой эффект лежит в основе известного магнитомеханического явления — намагничивания железного стержня при его вращении вокруг собственной оси — при этом спины электронов выстраиваются вдоль оси стержня (опыт Барнетта).
не совпадут. Такой эффект лежит в основе известного магнитомеханического явления — намагничивания железного стержня при его вращении вокруг собственной оси — при этом спины электронов выстраиваются вдоль оси стержня (опыт Барнетта).
Гироскопические усилия испытывают подшипники осей быстро вращающихся частей машины при повороте самой машины (турбины на корабле, винта на самолете и т.д.). При значительных величинах угловой скорости вынужденной прецессии  и собственного вращения
и собственного вращения  а также больших размерах маховика эти силы могут даже разрушить подшипники. Рассмотрим некоторые примеры проявления гироскопических сил.
а также больших размерах маховика эти силы могут даже разрушить подшипники. Рассмотрим некоторые примеры проявления гироскопических сил.

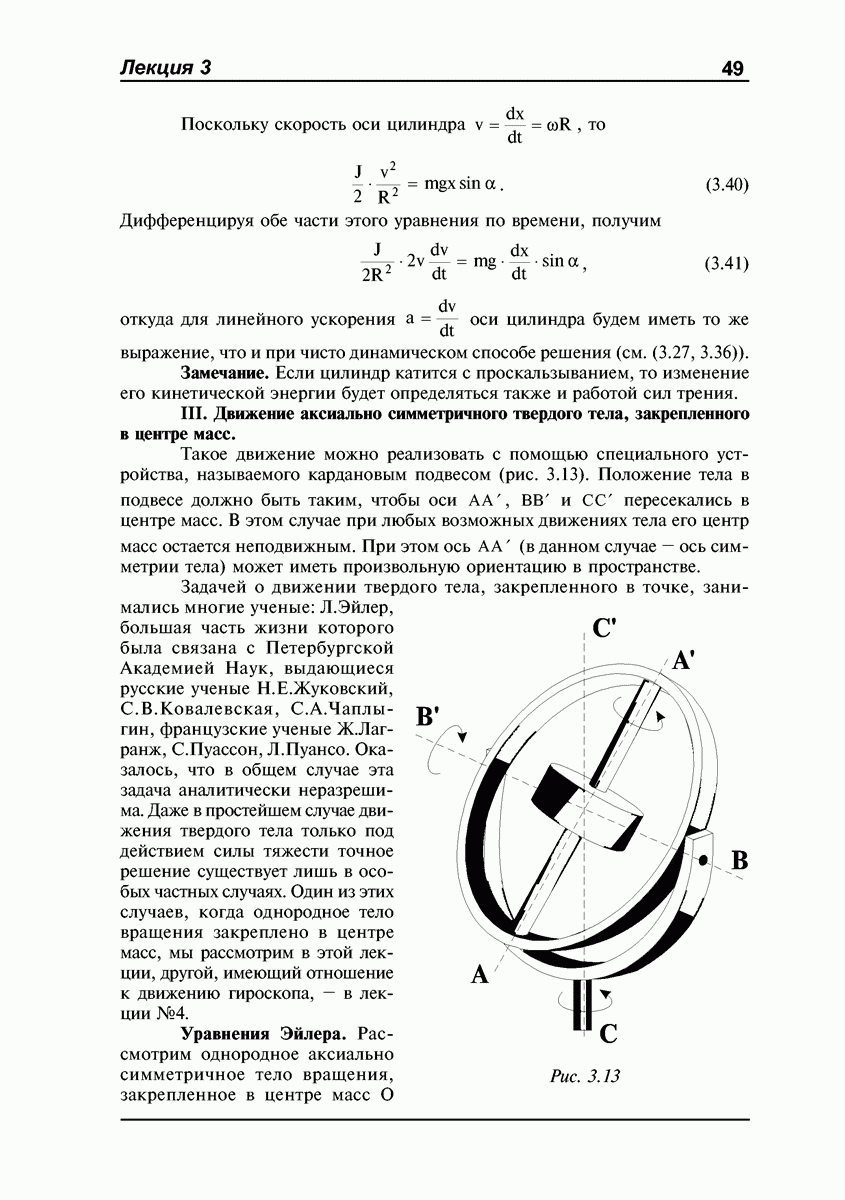
Рис. 4.11

Рис. 4.12
Пример 1. Легкий одномоторный самолет с правым винтом совершает левый вираж (рис. 4.12). Гироскопический момент передается через подшипники А и В на корпус самолета и действует на него, стремясь совместить ось собственного вращения винта (вектор со) с осью вынужденной прецессии (вектор  Самолет начинает задирать нос кверху, и летчик должен “дать ручку от себя”, то есть опустить вниз руль высоты. Таким образом, момент гироскопических сил будет компенсирован моментом аэродинамических сил.
Самолет начинает задирать нос кверху, и летчик должен “дать ручку от себя”, то есть опустить вниз руль высоты. Таким образом, момент гироскопических сил будет компенсирован моментом аэродинамических сил.
Пример 2. При килевой качке корабля (с носа на корму и обратно) ротор быстроходной турбины участвует в двух движениях: во вращении вокруг своей оси с угловой скоростью  и в повороте вокруг горизонтальной оси, перпендикулярной валу турбины, с угловой скоростью
и в повороте вокруг горизонтальной оси, перпендикулярной валу турбины, с угловой скоростью  (рис. 4.13). При этом вал турбины будет давить на подшипники с силами
(рис. 4.13). При этом вал турбины будет давить на подшипники с силами  лежащими в горизонтальной плоскости. При качке эти силы, как и гироскопический момент, периодически меняют свое направление на противоположное и могут вызвать “рыскание” корабля, если он не слишком велик (например, буксира).
лежащими в горизонтальной плоскости. При качке эти силы, как и гироскопический момент, периодически меняют свое направление на противоположное и могут вызвать “рыскание” корабля, если он не слишком велик (например, буксира).
Допустим, что масса турбины  кг, ее радиус инерции
кг, ее радиус инерции  скорость вращения турбины
скорость вращения турбины  об/мин, максимальная угловая скорость корпуса судна при килевой качке
об/мин, максимальная угловая скорость корпуса судна при килевой качке  расстояние между подшипниками
расстояние между подшипниками  Максимальное значение гироскопической силы, действующей на каждый из подшипников, составит
Максимальное значение гироскопической силы, действующей на каждый из подшипников, составит

После подстановки числовых данных получим  , то есть около 1 тонны.
, то есть около 1 тонны.
Пример 3. Гироскопические силы могут вызвать так называемые колебания “шимми” колес автомобиля (рис. 4.14) [9]. Колесу, вращающемуся вокруг оси  с угловой скоростью
с угловой скоростью  в момент наезда на препятствие сообщается дополнительная скорость вынужденного поворота вокруг оси, перпендикулярной плоскости рисунка. При этом возникает момент гироскопических сил, и колесо начнет поворачиваться вокруг оси
в момент наезда на препятствие сообщается дополнительная скорость вынужденного поворота вокруг оси, перпендикулярной плоскости рисунка. При этом возникает момент гироскопических сил, и колесо начнет поворачиваться вокруг оси  Приобретая угловую скорость поворота вокруг оси
Приобретая угловую скорость поворота вокруг оси  колесо снова начнет поворачиваться вокруг оси,
колесо снова начнет поворачиваться вокруг оси,

Рис. 4.13

Рис. 4.14
перпендикулярной плоскости рисунка. В результате возникают колебательные движения колеса вокруг двух взаимно перпендикулярныхосей: оси поворота  и оси, совмещенной с направлением движения автомобиля. Если в конструкции автомобиля не принять специальных мер, эти колебания могут привести к срыву покрышки с обода колеса и к поломке деталей его крепления. В современных конструкциях подвески колесо при наезде на препятствие практически остается в вертикальной плоскости.
и оси, совмещенной с направлением движения автомобиля. Если в конструкции автомобиля не принять специальных мер, эти колебания могут привести к срыву покрышки с обода колеса и к поломке деталей его крепления. В современных конструкциях подвески колесо при наезде на препятствие практически остается в вертикальной плоскости.
Пример 4. С гироскопическим эффектом мы сталкиваемся и при езде на велосипеде (рис. 4.15). Совершая, например, поворот направо, велосипедист инстинктивно смещает центр тяжести своего тела вправо, как бы заваливая велосипед. Возникшее принудительное вращение велосипеда с угловой скоростью О. приводит к появлению гироскопических сил с моментом М. На заднем колесе этот момент будет погашен в подшипниках, жестко связанных с рамой. Переднее же колесо, имеющее по отношению к раме свободу вращения в рулевой колонке, под действием гироскопического момента начнет поворачиваться как раз в том направлении, которое было необходимо для правого поворота велосипеда.
Опытные велосипедисты совершают подобные повороты, что называется, “без рук”.
Вопрос о возникновении гироскопических сил можно рассматривать и с другой точки зрения. Можно считать, что гироскоп, изображенный на рис. 4.10, участвует в двух одновременных движениях: относительном вращении вокруг собственной оси с угловой скоростью  и переносном, вынужденном повороте вокруг вертикальной оси с угловой скоростью
и переносном, вынужденном повороте вокруг вертикальной оси с угловой скоростью  Таким образом, элементарные массы
Таким образом, элементарные массы  на которые можно разбить диск гироскопа (маленькие кружки на рис. 4.16), должны испытывать кориолисовы ускорения
на которые можно разбить диск гироскопа (маленькие кружки на рис. 4.16), должны испытывать кориолисовы ускорения

Рис. 4.15

Рис. 4.16

Эти ускорения будут максимальны для масс, находящихся в данный момент времени на вертикальном диаметре диска, и равны нулю для масс, которые находятся на горизонтальном диаметре (рис. 4.16).
В системе отсчета, вращающейся с угловой скоростью  (в этой системе отсчета ось гироскопа неподвижна), на массы
(в этой системе отсчета ось гироскопа неподвижна), на массы  будут действовать кориолисовы силы инерции
будут действовать кориолисовы силы инерции

Эти силы создают момент М, который стремится повернуть ось гироскопа таким образом, чтобы вектор  совместился с
совместился с  Момент М должен быть уравновешен моментом сил реакции
Момент М должен быть уравновешен моментом сил реакции  (рис. 4.10), действующих на ось гироскопа со стороны подшипников. По третьему закону Ньютона, ось будет действовать на подшипники, а через них и на раму, в которой эта ось закреплена, с гироскопическими силами
(рис. 4.10), действующих на ось гироскопа со стороны подшипников. По третьему закону Ньютона, ось будет действовать на подшипники, а через них и на раму, в которой эта ось закреплена, с гироскопическими силами  Поэтому и говорят, что гироскопические силы обусловлены силами Кориолиса.
Поэтому и говорят, что гироскопические силы обусловлены силами Кориолиса.
Возникновение кориолисовых сил можно легко продемонстрировать, если вместо жесткого диска гироскопа взять гибкий резиновый диск (рис. 4.17). При повороте вала с раскрученным диском вокруг вертикальной оси он изгибается в направлении действия кориолисовых сил так, как изображено на рис. 4.17.

Рис. 4.17
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- ЛЕКЦИЯ №1. Кинематика абсолютно твердого тела. Степени свободы. Углы Эйлера. Поступательное движение. Вращение вокруг неподвижной оси. Плоское движение. Движение твердого тела, имеющего одну неподвижную точку. Движение свободного твердого тела.
- Поступательное движение
- Вращение вокруг неподвижной оси
- Плоское движение
- Движение твердого тела с одной неподвижной точкой.
- Движение свободного твердого тела.
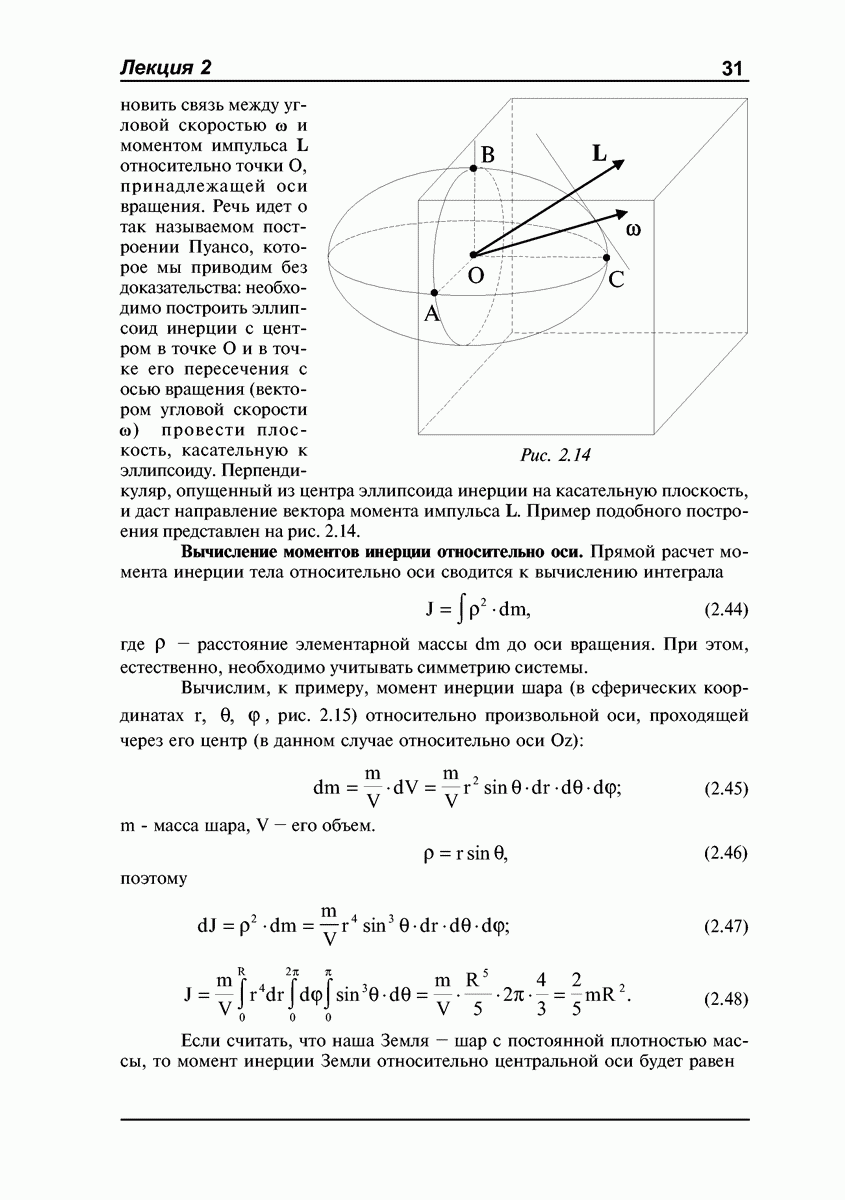
- ЛЕКЦИЯ №2. Динамика абсолютно твердого тела. Момент импульса. Тензор инерции. Момент импульса тела относительно оси. Эллипсоид инерции. Вычисление моментов инерции относительно оси. Теорема Гюйгенса-Штейнера. Момент импульса относительно движущегося центра масс.
- Главные оси инерции.
- Момент импульса твердого тела относительно оси. Момент инерции относительно оси.
- Эллипсоид инерции.
- Вычисление моментов инерции относительно оси.
- Теорема Гюйгенса-Штейнера.
- Момент импульса тела относительно движущегося центра масс.
- ЛЕКЦИЯ №3. Динамика абсолютно твердого тела. Уравнение поступательного движения и уравнение моментов. Вращение твердого тела вокруг неподвижной оси. Центр удара. Динамика плоского движения твердого тела. Движение аксиально симметричного твердого тела, закрепленного в центре масс. Уравнения Эйлера.
- Уравнения динамики твердого тела. Общий случай.
- Кинетическая энергия вращающегося тела и работа внешних сил (ось вращения неподвижна).
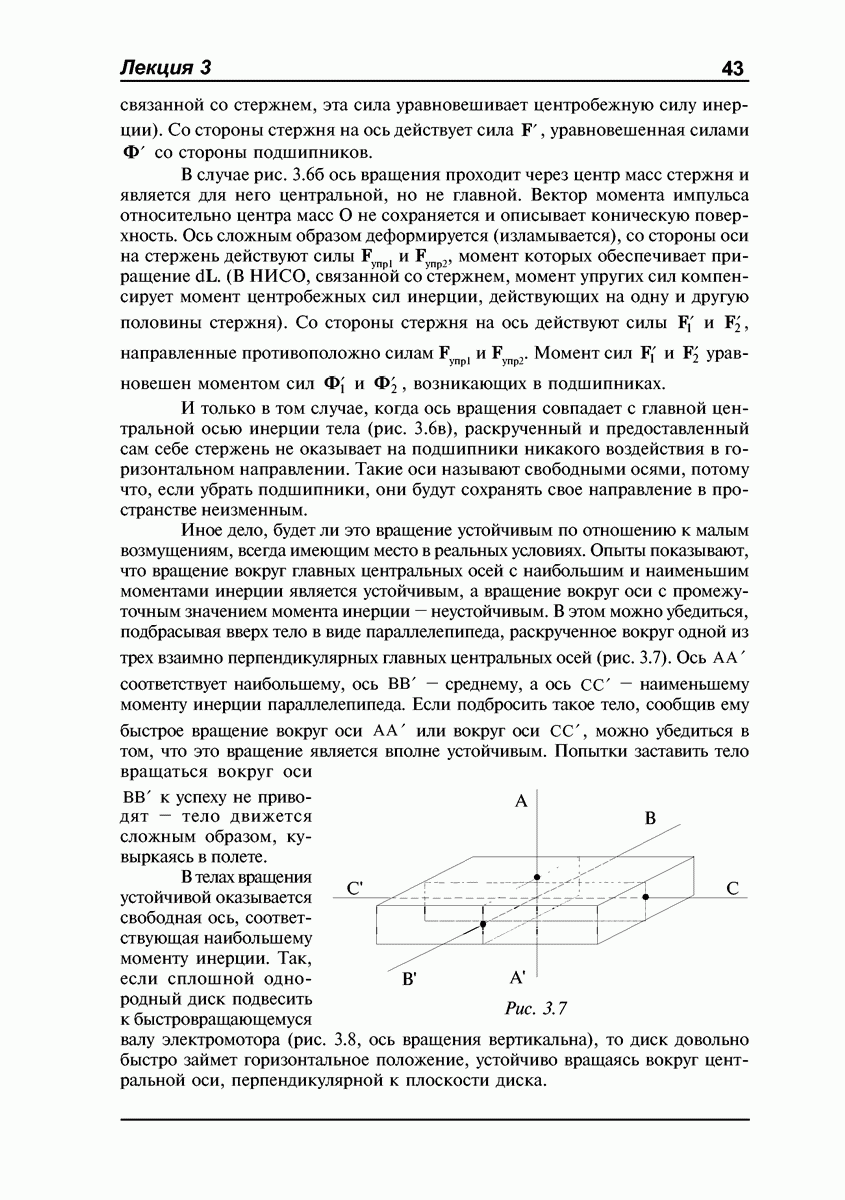
- Свободные оси. Устойчивость свободного вращения.
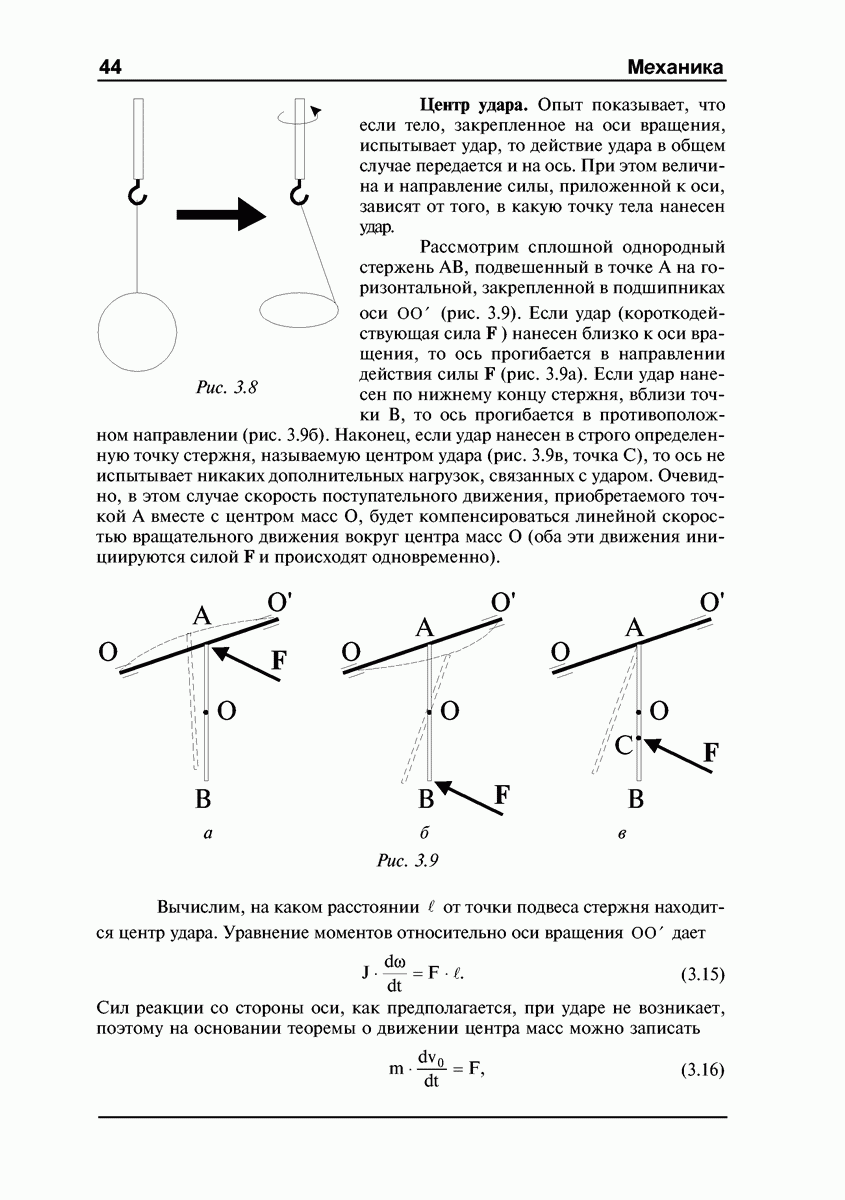
- Центр удара.
- Кинетическая энергия при плоском движении.
- Уравнения Эйлера.
- ЛЕКЦИЯ №4. Гироскопы. Свободный гироскоп. Прецессия гироскопа под действием внешних сил. Угловая скорость прецессии. Нутации. Гироскопические силы, их природа и проявления.
- Свободный гироскоп.
- Прецессия гироскопа под действием внешних сил. Элементарная теория.
- Прецессия гироскопа под действием внешних сил. Отход от элементарной теории. Нутации.
- Гироскопические силы.
- Волчки.
- ЛИТЕРАТУРА