| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Кинетическая энергия при плоском движении.
Кинетическая энергия твердого тела представляет собой сумму кинетических энергий отдельных частиц:

где  — скорость центра масс тела,
— скорость центра масс тела,  — скорость
— скорость  частицы относительно системы координат, связанной с центром масс и совершающей поступательное движение вместе с ним. Возводя сумму скоростей в квадрат, получим:
частицы относительно системы координат, связанной с центром масс и совершающей поступательное движение вместе с ним. Возводя сумму скоростей в квадрат, получим:

так как  (суммарный импульс частиц в системе центра масс равен нулю).
(суммарный импульс частиц в системе центра масс равен нулю).
Таким образом, кинетическая энергия при плоском движении равна сумме кинетических энергий поступательного и вращательного движений (теорема Кёнига). Если рассматривать плоское движение как вращение вокруг мгновенной оси, то кинетическая энергия тела есть энергия вращательного движения.
В этой связи задачу о скатывании цилиндра с наклонной плоскости можно решить, используя закон сохранения механической энергии (напомним, что сила трения при качении без проскальзывания работу не совершает).
Приращение кинетической энергии цилиндра равно убыли его потенциальной энергии:

Здесь  — смещение цилиндра вдоль наклонной плоскости,
— смещение цилиндра вдоль наклонной плоскости,  — момент инерции цилиндра относительно мгновенной оси вращения.
— момент инерции цилиндра относительно мгновенной оси вращения.
Поскольку скорость оси цилиндра  то
то

Дифференцируя обе части этого уравнения по времени, получим

откуда для линеиного ускорения  оси цилиндра будем иметь то же выражение, что и при чисто динамическом способе решения (см. (3.27, 3.36)).
оси цилиндра будем иметь то же выражение, что и при чисто динамическом способе решения (см. (3.27, 3.36)).
Замечание. Если цилиндр катится с проскальзыванием, то изменение его кинетической энергии будет определяться также и работой сил трения.
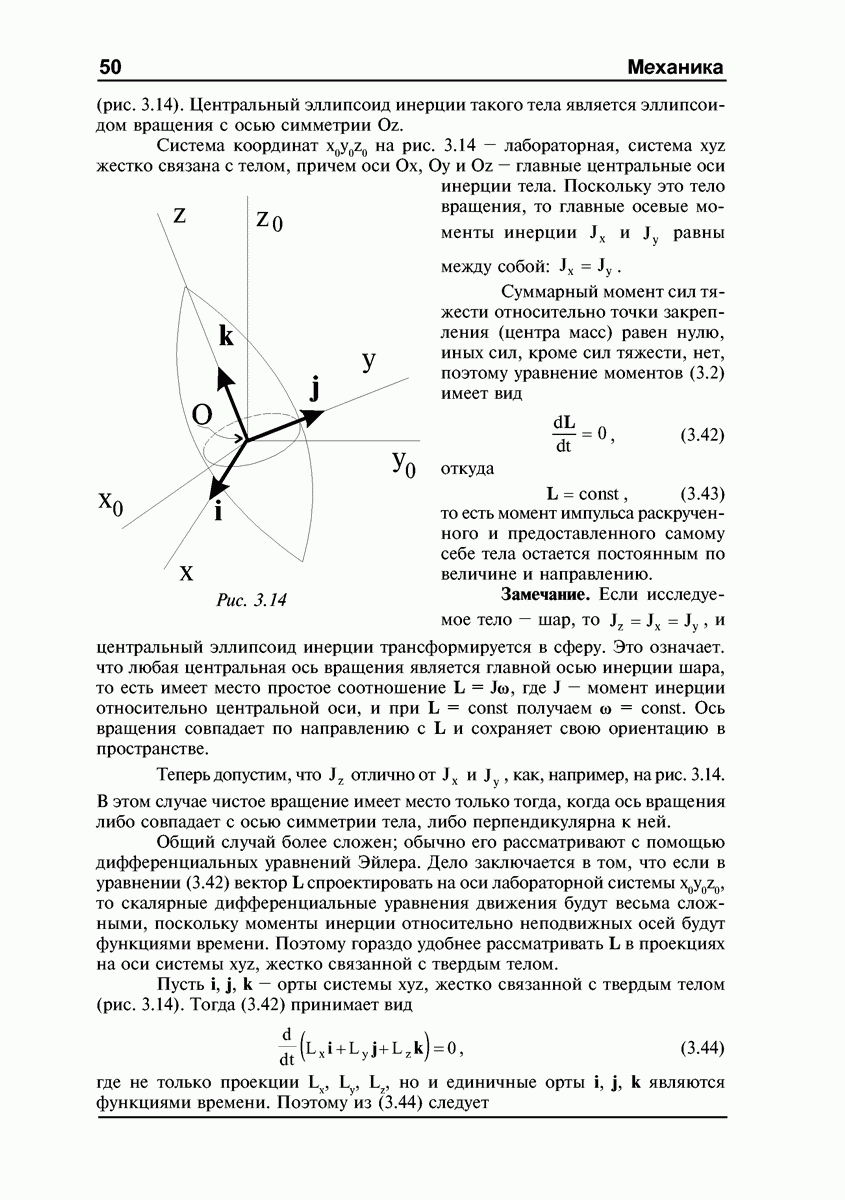
III. Движение аксиально симметричного твердого тела, закрепленного в центре масс.
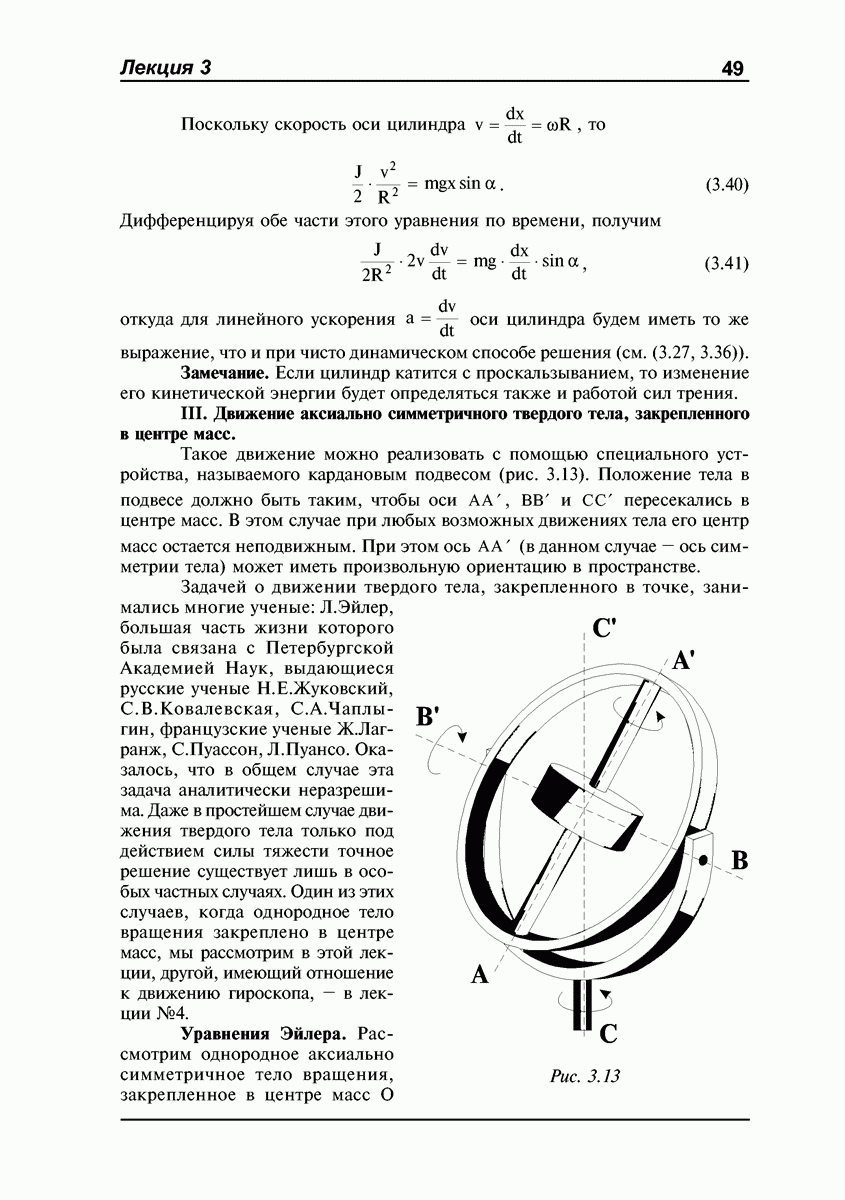
Такое движение можно реализовать с помощью специального устройства, называемого кардановым подвесом (рис. 3.13). Положение тела в подвесе должно быть таким, чтобы оси  и
и  пересекались в центре масс. В этом случае при любых возможных движениях тела его центр масс остается неподвижным. При этом ось
пересекались в центре масс. В этом случае при любых возможных движениях тела его центр масс остается неподвижным. При этом ось  (в данном случае — ось симметрии тела) может иметь произвольную ориентацию в пространстве.
(в данном случае — ось симметрии тела) может иметь произвольную ориентацию в пространстве.
Задачей о движении твердого тела, закрепленного в точке, занимались многие ученые: Л.Эйлер, большая часть жизни которого была связана с Петербургской Академией Наук, выдающиеся русские ученые Н.Е.Жуковский, С.В.Ковалевская, С.А.Чаплыгин, французские ученые Ж.Лагранж, С.Пуассон, Л.Пуансо. Оказалось, что в общем случае эта задача аналитически неразрешима. Даже в простейшем случае движения твердого тела только под действием силы тяжести точное решение существует лишь в особых частных случаях. Один из этих случаев, когда однородное тело вращения закреплено в центре масс, мы рассмотрим в этой лекции, другой, имеющий отношение к движению гироскопа, — в лекции №4.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- ЛЕКЦИЯ №1. Кинематика абсолютно твердого тела. Степени свободы. Углы Эйлера. Поступательное движение. Вращение вокруг неподвижной оси. Плоское движение. Движение твердого тела, имеющего одну неподвижную точку. Движение свободного твердого тела.
- Поступательное движение
- Вращение вокруг неподвижной оси
- Плоское движение
- Движение твердого тела с одной неподвижной точкой.
- Движение свободного твердого тела.
- ЛЕКЦИЯ №2. Динамика абсолютно твердого тела. Момент импульса. Тензор инерции. Момент импульса тела относительно оси. Эллипсоид инерции. Вычисление моментов инерции относительно оси. Теорема Гюйгенса-Штейнера. Момент импульса относительно движущегося центра масс.
- Главные оси инерции.
- Момент импульса твердого тела относительно оси. Момент инерции относительно оси.
- Эллипсоид инерции.
- Вычисление моментов инерции относительно оси.
- Теорема Гюйгенса-Штейнера.
- Момент импульса тела относительно движущегося центра масс.
- ЛЕКЦИЯ №3. Динамика абсолютно твердого тела. Уравнение поступательного движения и уравнение моментов. Вращение твердого тела вокруг неподвижной оси. Центр удара. Динамика плоского движения твердого тела. Движение аксиально симметричного твердого тела, закрепленного в центре масс. Уравнения Эйлера.
- Уравнения динамики твердого тела. Общий случай.
- Кинетическая энергия вращающегося тела и работа внешних сил (ось вращения неподвижна).
- Свободные оси. Устойчивость свободного вращения.
- Центр удара.
- Кинетическая энергия при плоском движении.
- Уравнения Эйлера.
- ЛЕКЦИЯ №4. Гироскопы. Свободный гироскоп. Прецессия гироскопа под действием внешних сил. Угловая скорость прецессии. Нутации. Гироскопические силы, их природа и проявления.
- Свободный гироскоп.
- Прецессия гироскопа под действием внешних сил. Элементарная теория.
- Прецессия гироскопа под действием внешних сил. Отход от элементарной теории. Нутации.
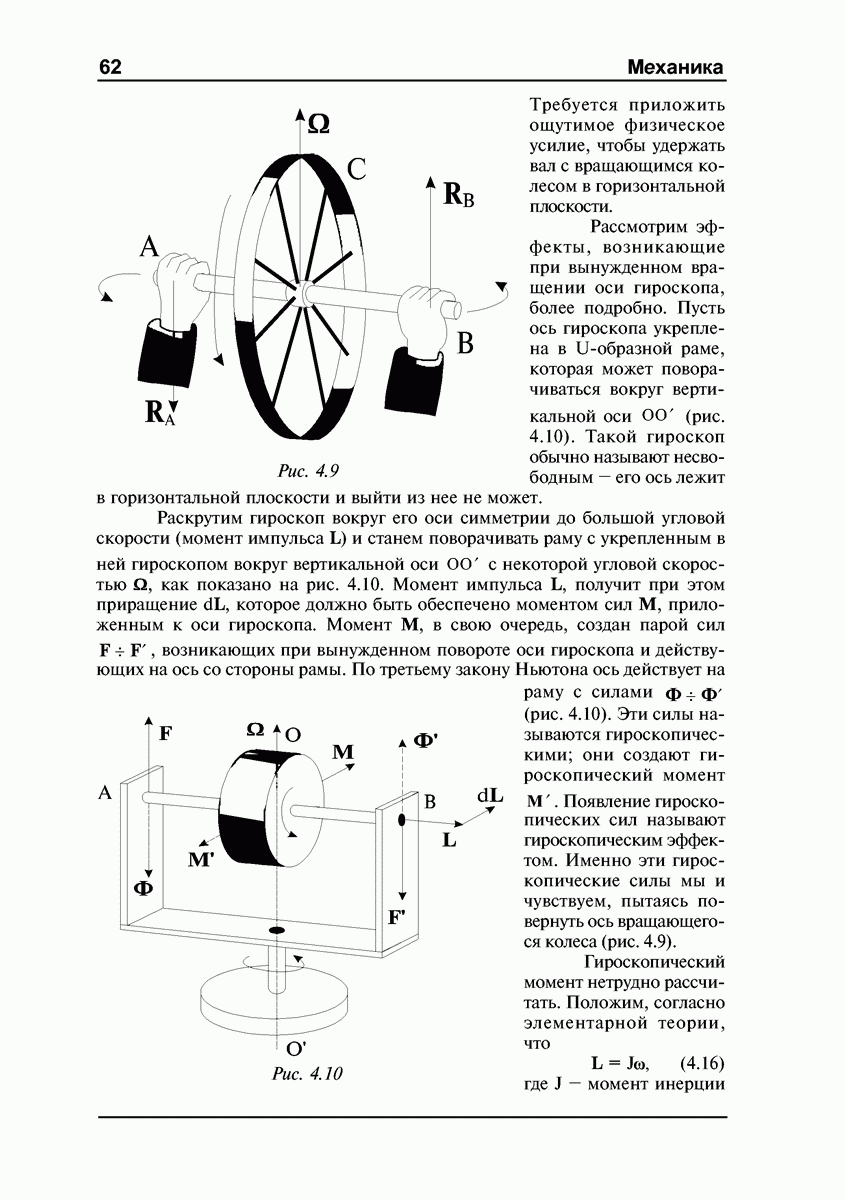
- Гироскопические силы.
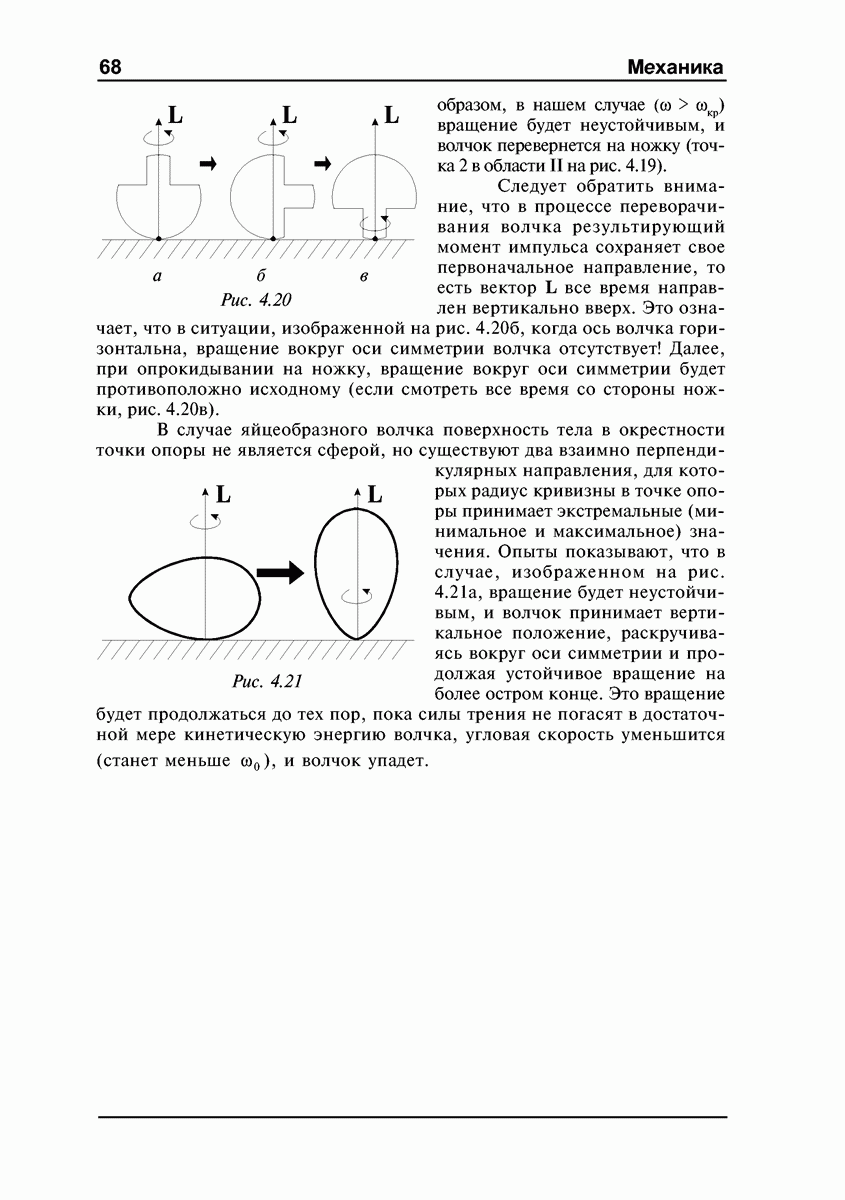
- Волчки.
- ЛИТЕРАТУРА