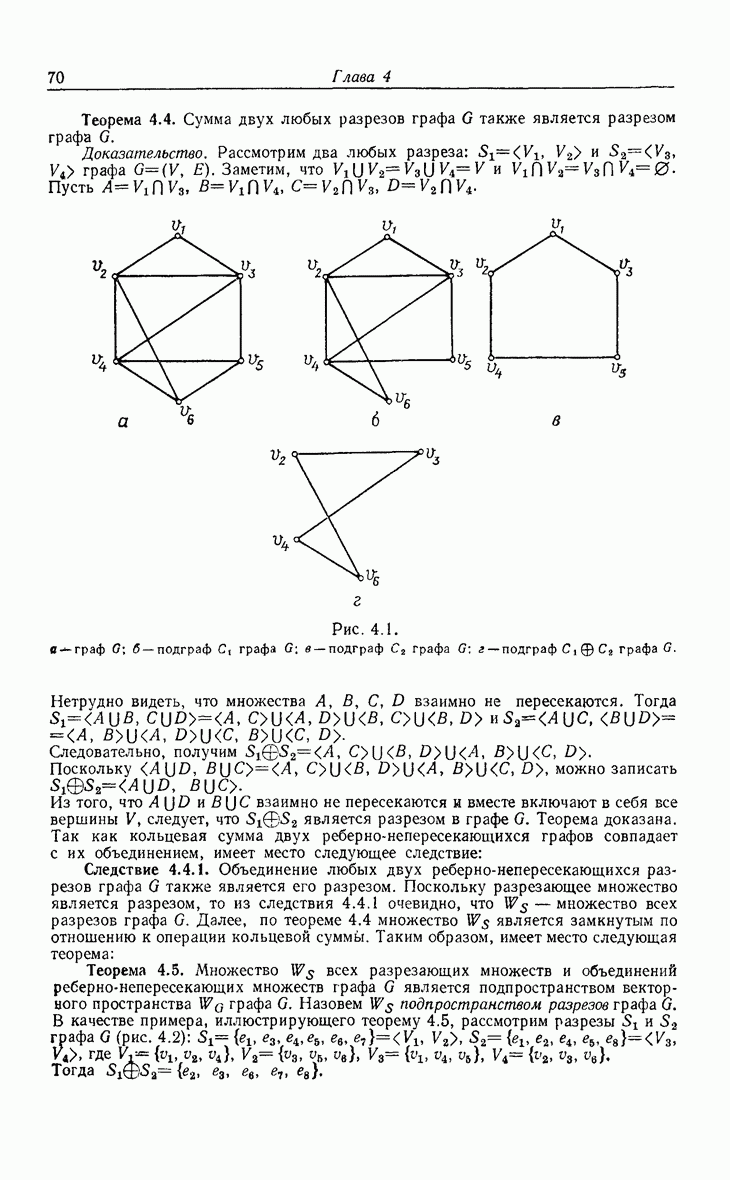
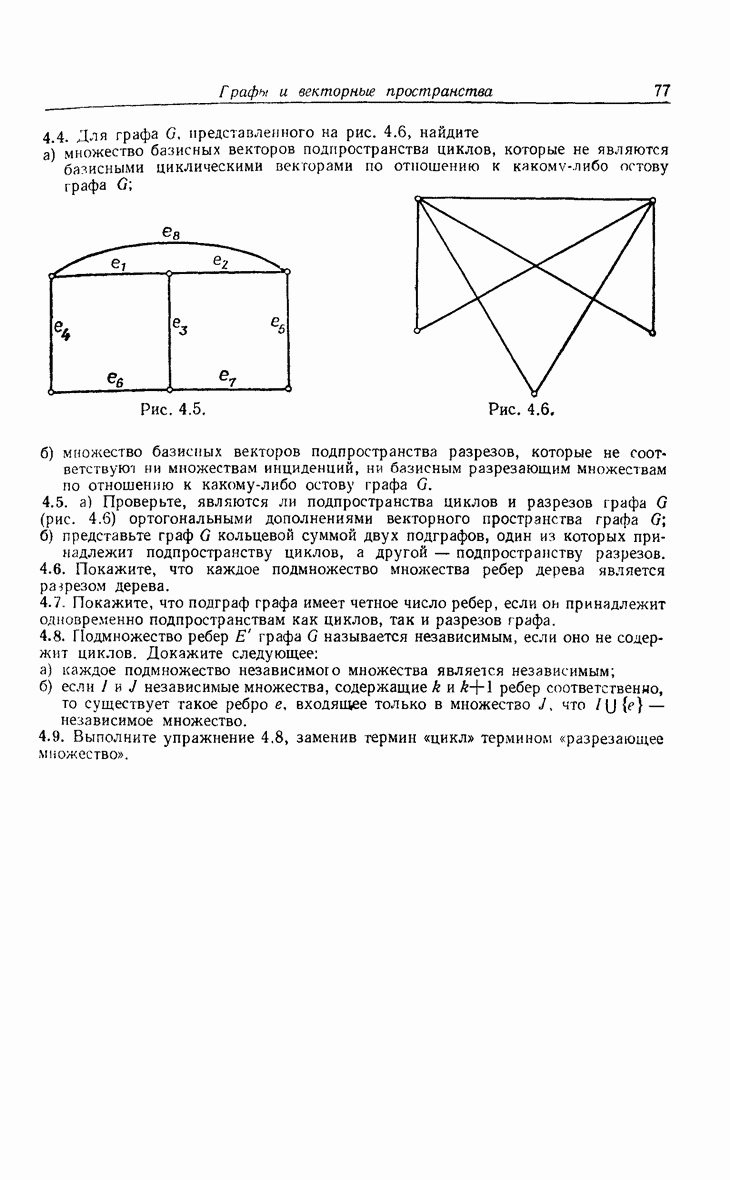
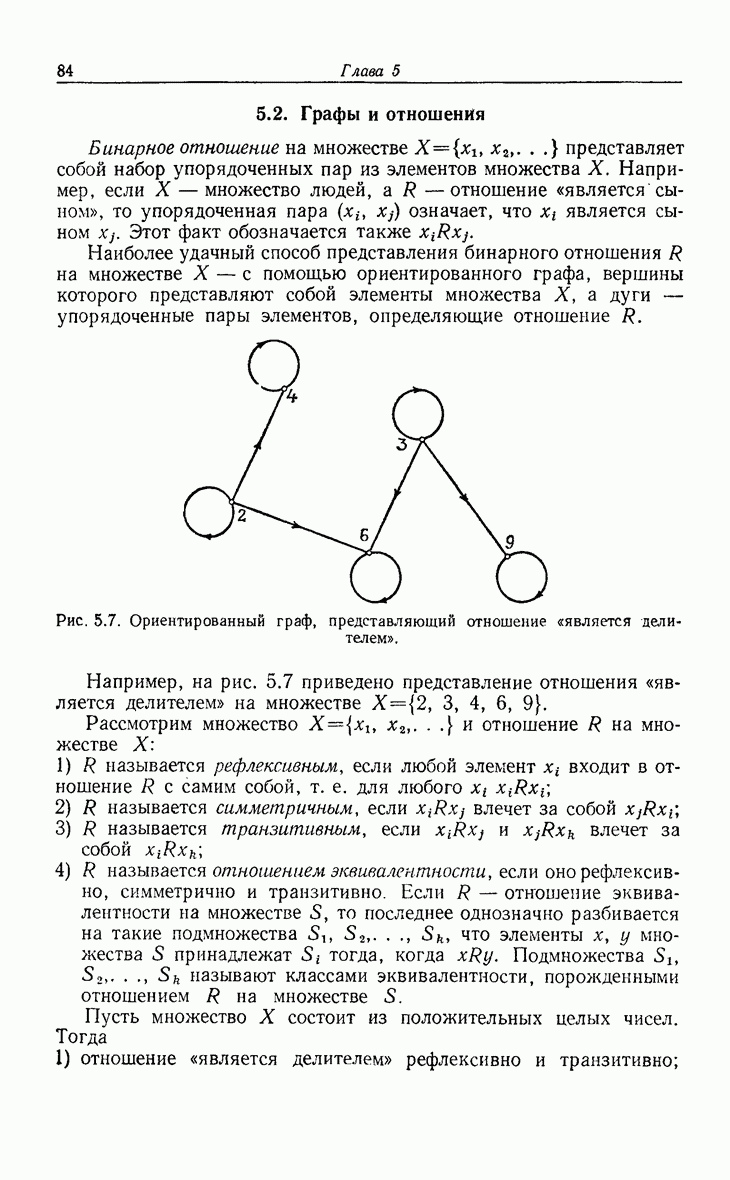
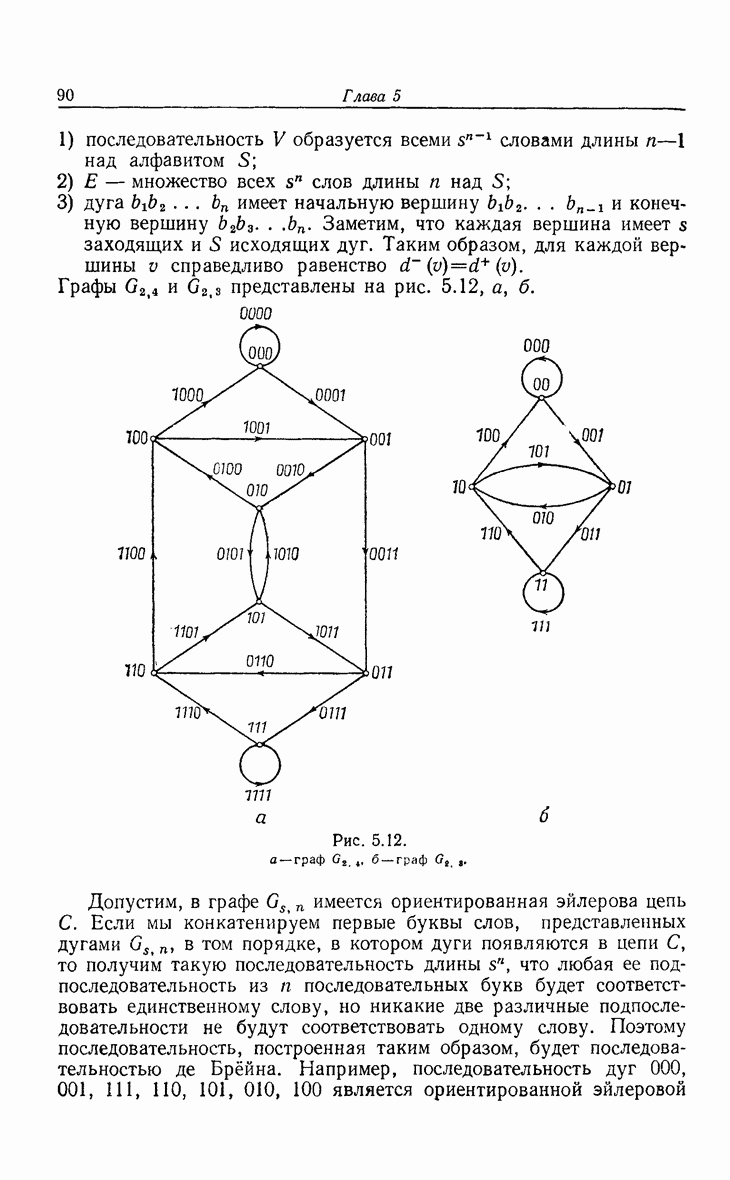
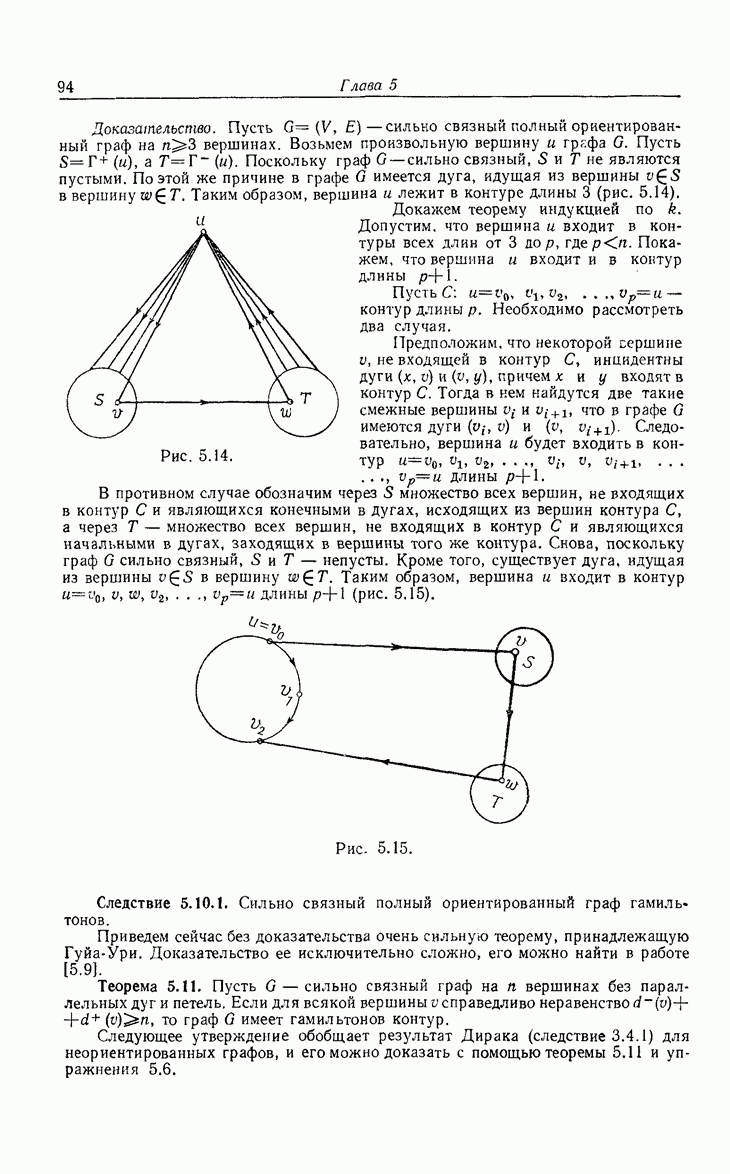
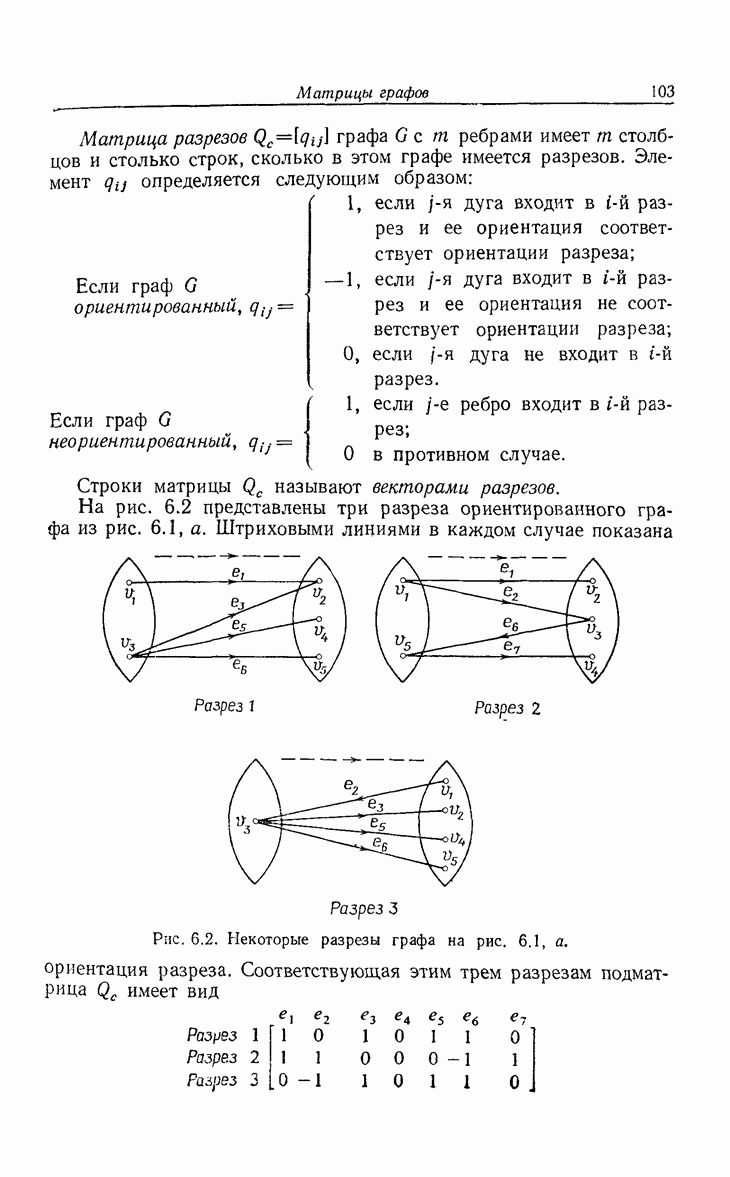
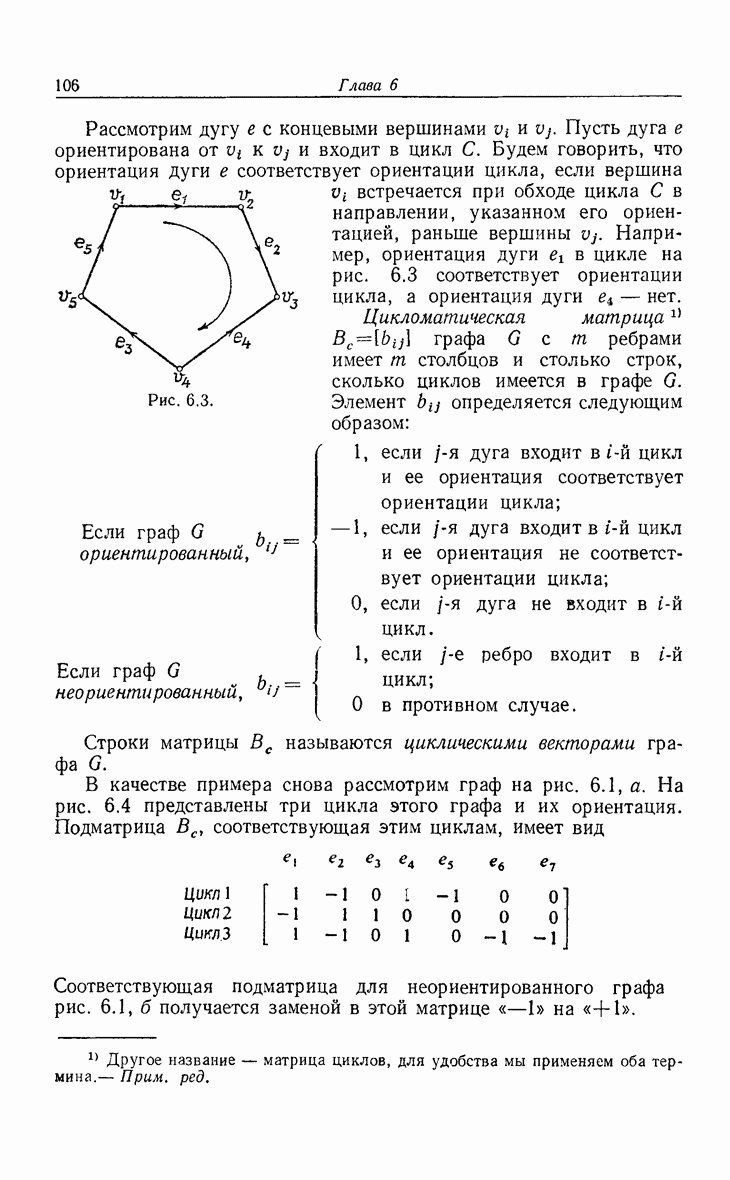
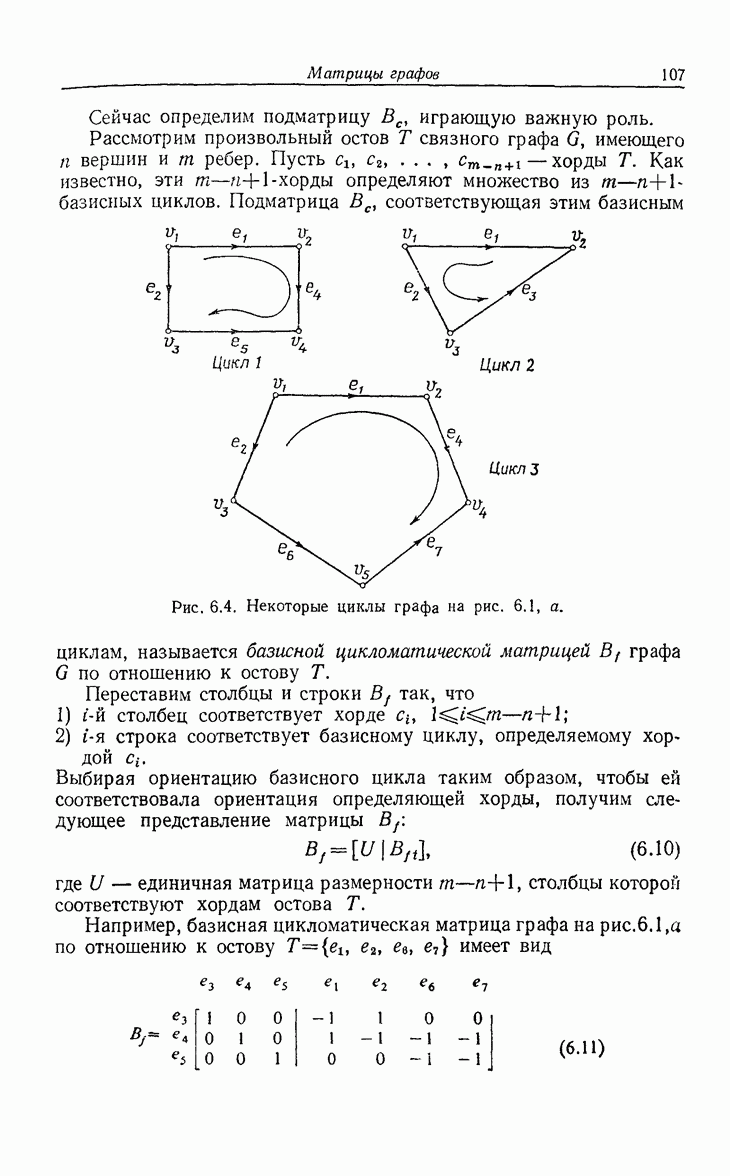
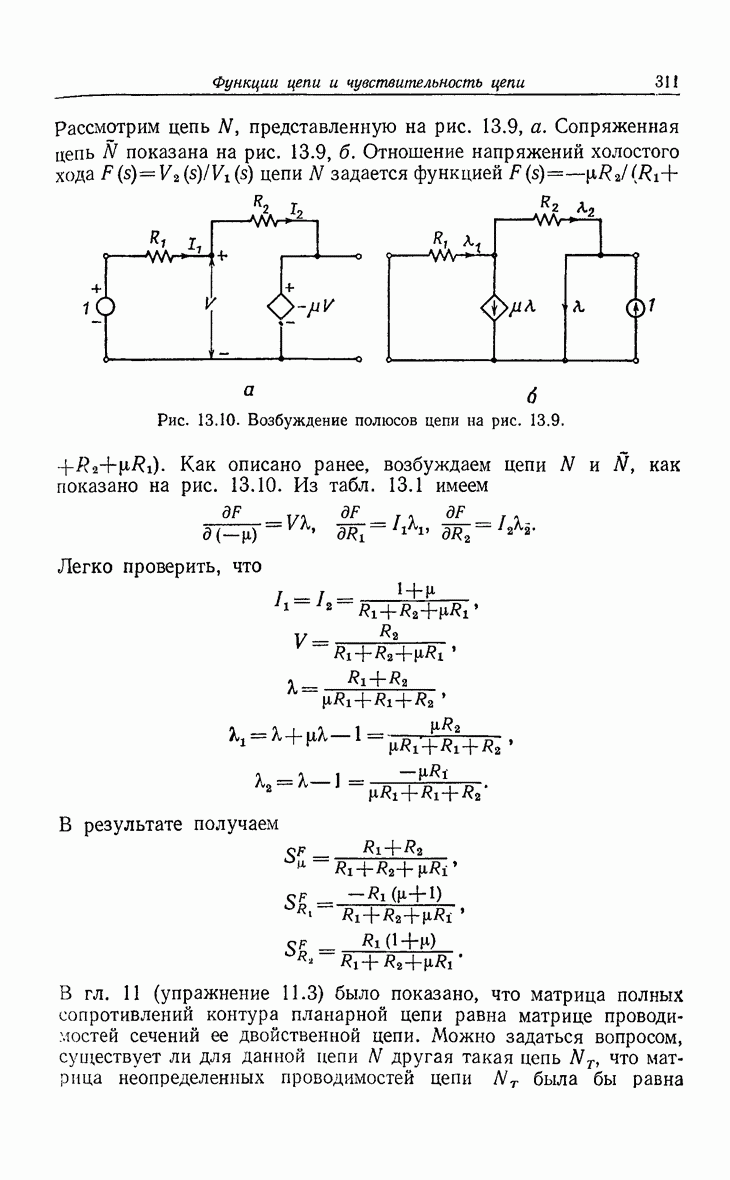
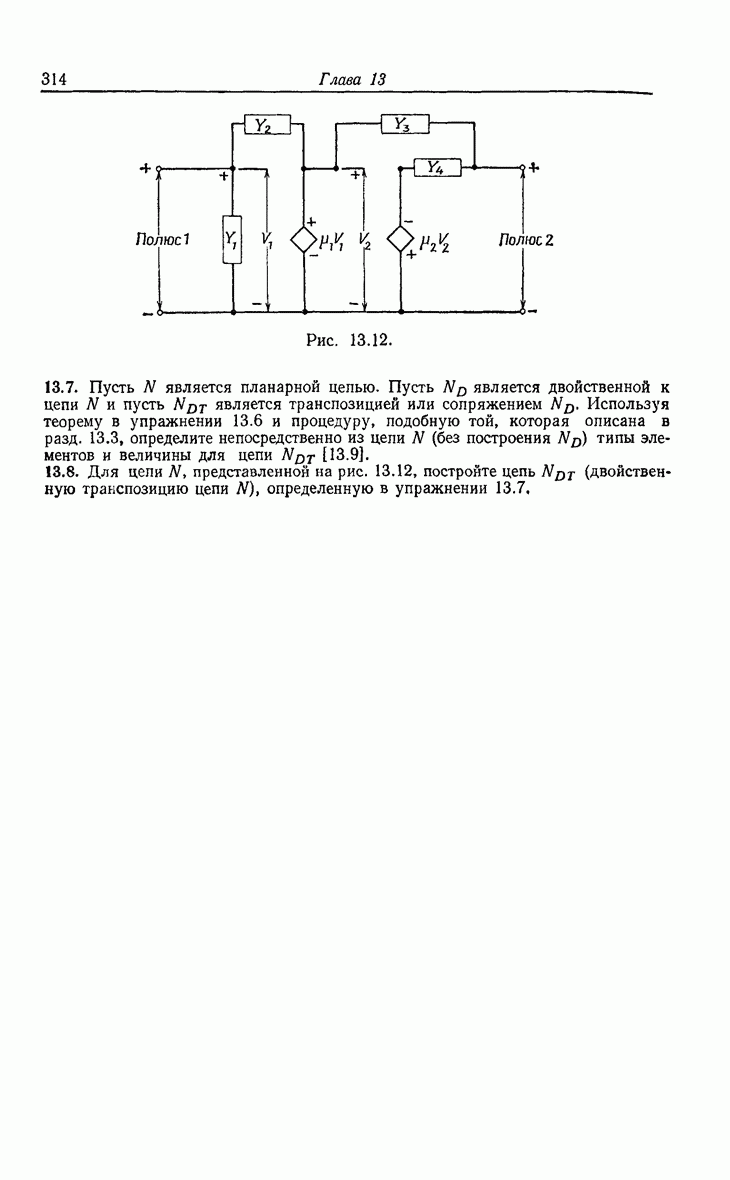
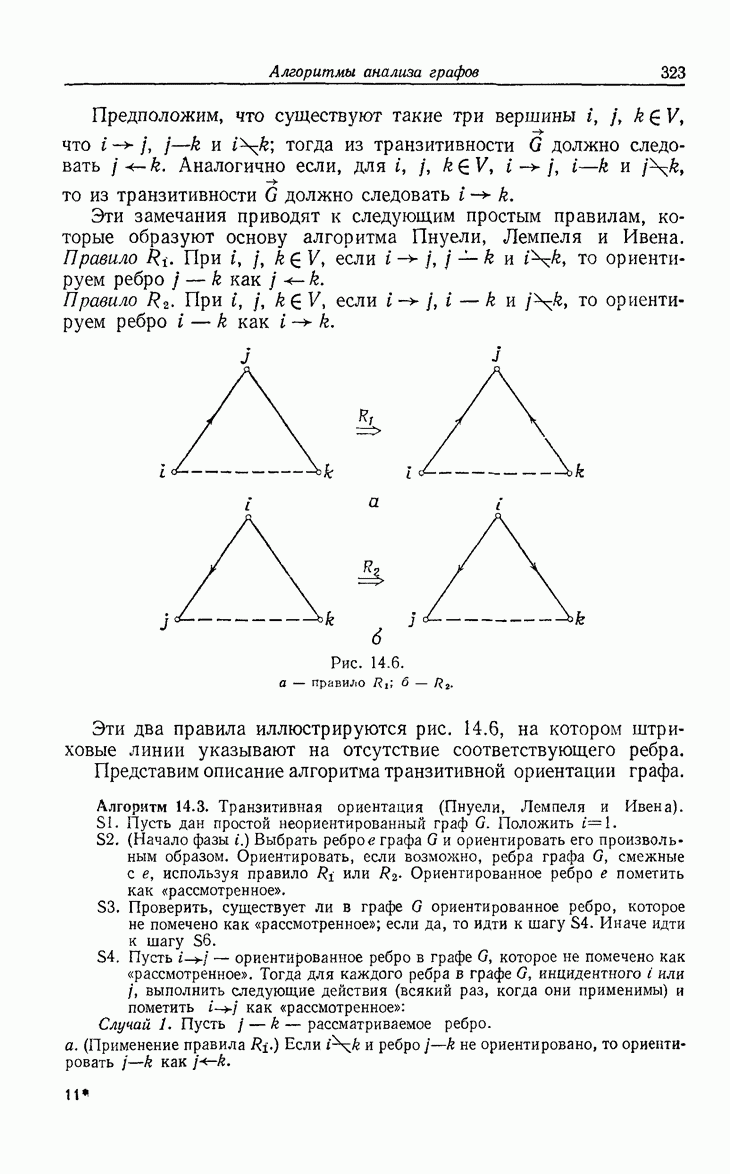
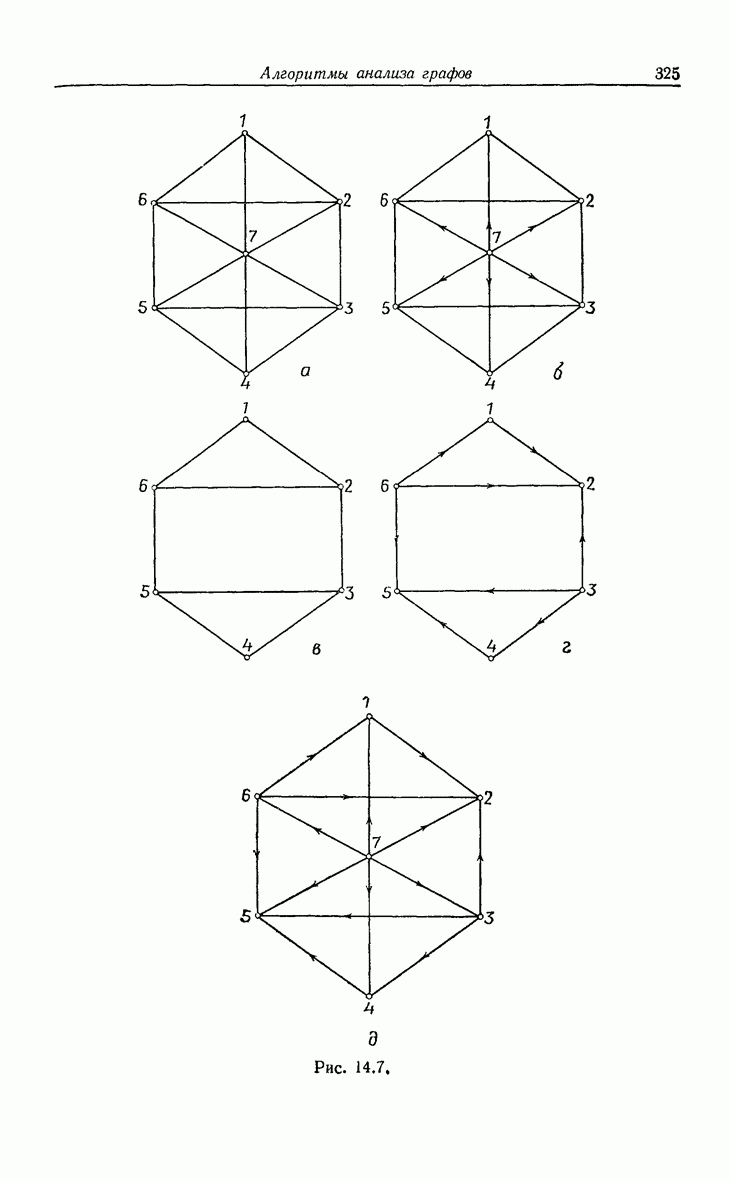
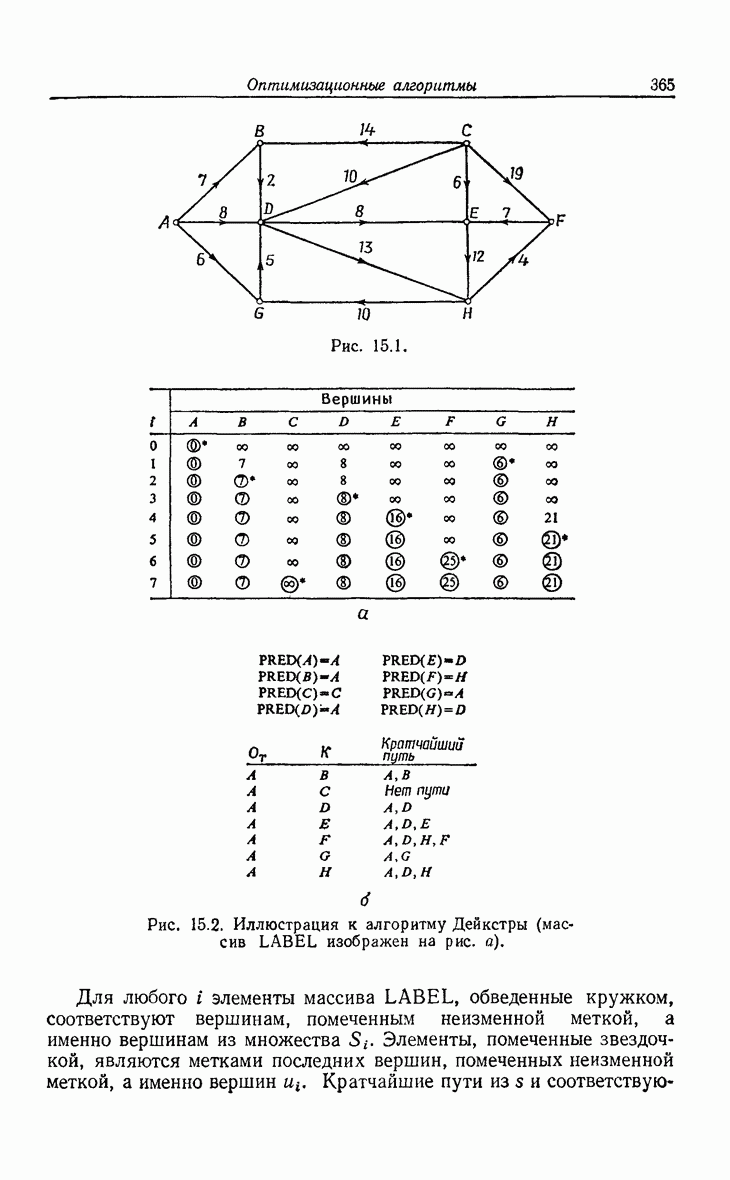
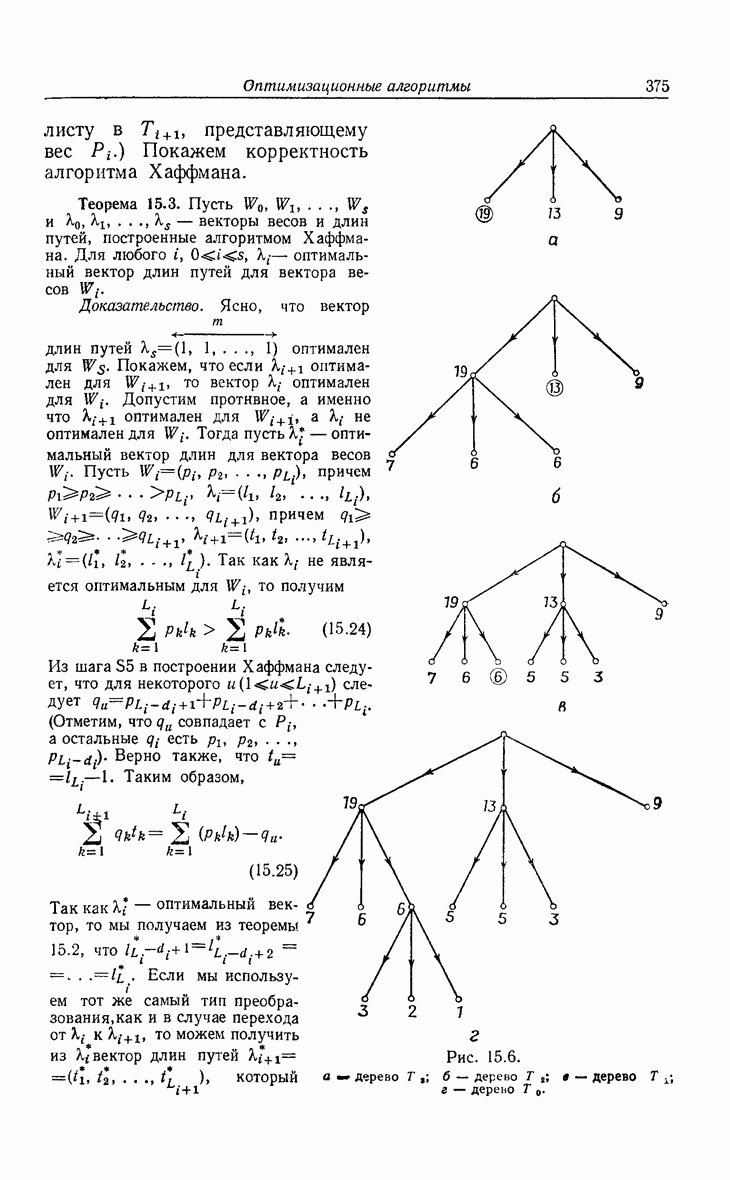
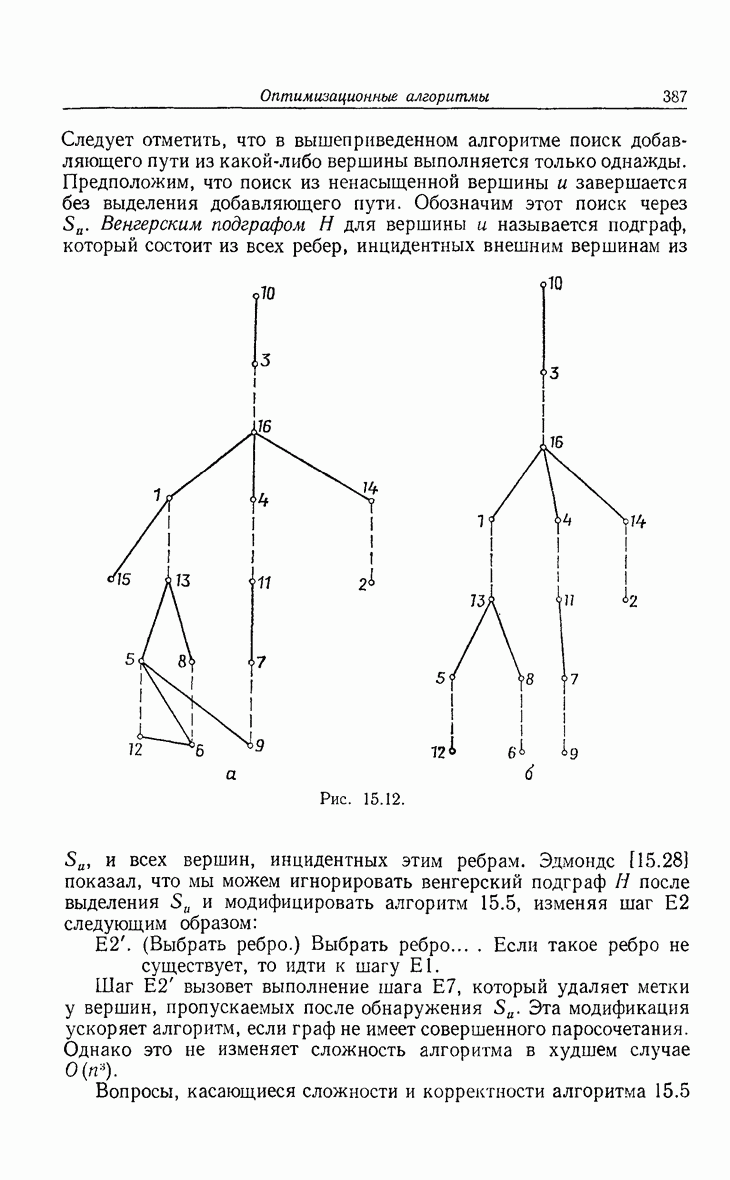
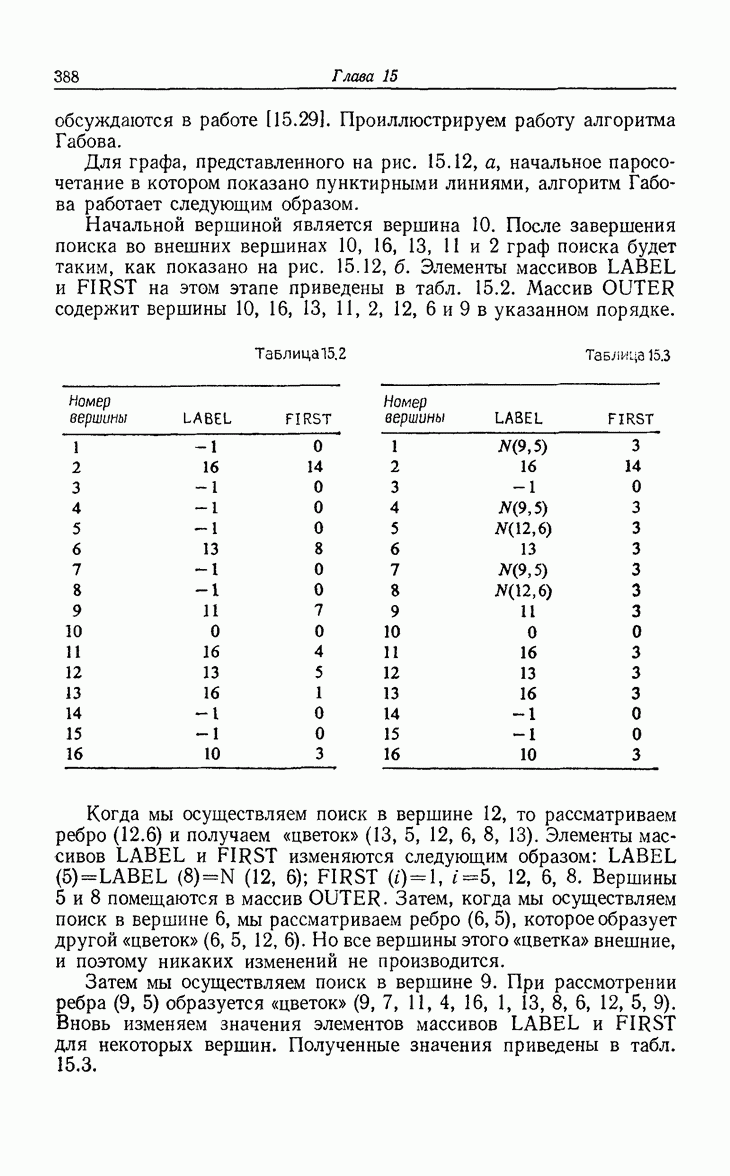
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10.3. Эквивалентные системы аксиом
В этом разделе мы сформулируем несколько альтернативных систем аксиом, определяющих матроид. Эти эквивалентные характеризации помогут нам в более глубоком проникновении в структуру матроидов. Начнем с эквивалентного аксиомам независимости набора.
Теорема 10.6. (Аксиомы независимости.) Набор  подмножеств множества S составляет множество независимых множеств матроида тогда и только тогда, когда
подмножеств множества S составляет множество независимых множеств матроида тогда и только тогда, когда  удовлетворяет аксиомам 1.1, 1.2 и 1.3. Если А — произвольное подмножество множества 5, то все максимальные подмножества УА, входящие в
удовлетворяет аксиомам 1.1, 1.2 и 1.3. Если А — произвольное подмножество множества 5, то все максимальные подмножества УА, входящие в  имеют одинаковую мощность.
имеют одинаковую мощность.
Доказательство предлагается читателю в качестве упражнения. См. следствие 10.2.3.
Теорема 10.7. (Аксиомы баз.) Пусть  — множество баз матроида. Тогда
— множество баз матроида. Тогда  и никакое множество в
и никакое множество в  не содержит в качестве собственного подмножества другое.
не содержит в качестве собственного подмножества другое.
В.2. Если  тогда существует
тогда существует  такой, что
такой, что  Обратно, если
Обратно, если  -набор подмножеств S, удовлетворяющих аксиомам
-набор подмножеств S, удовлетворяющих аксиомам  то
то  для некоторого
для некоторого  является набором независимых множеств матроида на
является набором независимых множеств матроида на 
Доказательство. Мы уже доказали, что базы матроида удовлетворяют аксиомам  (Вспомните определение базы и следствие 10.2.3.)
(Вспомните определение базы и следствие 10.2.3.)
Пусть дан набор 33, удовлетворяющий аксиомам  Покажем, что набор
Покажем, что набор  определенный в формулировке теоремы, является набором независимых множеств матроида на
определенный в формулировке теоремы, является набором независимых множеств матроида на 
Прежде всего заметим, что из аксиом  следует существование для
следует существование для  такого
такого  что
что  входит в
входит в 
Очевидно, что удовлетворяет аксиомам 1.1 и 1.2. Для доказательства удовлетворения аксиоме 1.3 мы сначала покажем, что все члены 33 имеют одинаковую мощность.
Допустим, что существуют  Тогда, повторяя применение аксиомы
Тогда, повторяя применение аксиомы  мы сможем удалить
мы сможем удалить  из
из  и заменить это подмножество на такое множество
и заменить это подмножество на такое множество  с
с  что
что  будет членом
будет членом  Но
Но  что противоречит аксиоме
что противоречит аксиоме  Таким образом, все члены набора
Таким образом, все члены набора  имеют одинаковую мощность.
имеют одинаковую мощность.
Рассмотрим теперь два любых различных члена X и Y набора  с
с  Пусть
Пусть  , где
, где  . Пусть
. Пусть 
Рассмотрим множество  . По аксиоме
. По аксиоме  существует такой
существует такой  что
что  входит в
входит в  Если
Если  то
то  и, следовательно, является членом
и, следовательно, является членом  . Поэтому аксиома 1.3 в этом случае удовлетворяется.
. Поэтому аксиома 1.3 в этом случае удовлетворяется.
Если  , то рассмотрим
, то рассмотрим  . Снова по аксиоме
. Снова по аксиоме  существует такой
существует такой  , что
, что  является членом
является членом  Если
Если  то
то  . Следовательно,
. Следовательно,  и аксиома 1.3 удовлетворяется.
и аксиома 1.3 удовлетворяется.
Если  удалим из В" член
удалим из В" член  и т. д. Поскольку
и т. д. Поскольку  не более чем через q шагов мы достигнем ситуации, в которой заменим некоторый 6,- на элемент К, посредством чего выполним аксиому 1.3.
не более чем через q шагов мы достигнем ситуации, в которой заменим некоторый 6,- на элемент К, посредством чего выполним аксиому 1.3.
Теорема 10.8. (Аксиомы ранга.) Функция ранга  матроида М на множестве удовлетворяет аксиомам
матроида М на множестве удовлетворяет аксиомам
R.1.  для любого
для любого 

R.3. Для любых 
Обратно, если определенная на конечном множестве 5 целочисленная функция  удовлетворяет аксиомам
удовлетворяет аксиомам  то множество
то множество  является набором независимых множеств матроида на
является набором независимых множеств матроида на 
Доказательство. Мы уже доказали в теореме 10.3, что функция ранга матроида удовлетворяет аксиомам 
Для доказательства обратного предположим, что функция  удовлетворяет аксиомам
удовлетворяет аксиомам  Из аксиомы
Из аксиомы  следует, что
следует, что  Поэтому 0 в аксиома 1.1 удовлетворяется.
Поэтому 0 в аксиома 1.1 удовлетворяется.
Пусть  и АВ. Тогда по аксиоме
и АВ. Тогда по аксиоме  получаем
получаем

Если  то по аксиоме
то по аксиоме  что противоречит формуле (10.3). Следовательно,
что противоречит формуле (10.3). Следовательно,  и А также является членом
и А также является членом  , вследствие чего удовлетворяется аксиома 1.2.
, вследствие чего удовлетворяется аксиома 1.2.
Для доказательства аксиомы 1.3 заметим сначала, что из аксиом  следует аксиома
следует аксиома
R.3. Еслир  то
то  Пусть X и К — различные члены
Пусть X и К — различные члены  Предположим, что для любого
Предположим, что для любого  . Тогда, применяя повторно аксиому
. Тогда, применяя повторно аксиому  получим
получим  противоречие с
противоречие с  . Поэтому существует элемент
. Поэтому существует элемент  для которого
для которого  и аксиома 1.3, таким образом, удовлетворяется.
и аксиома 1.3, таким образом, удовлетворяется.
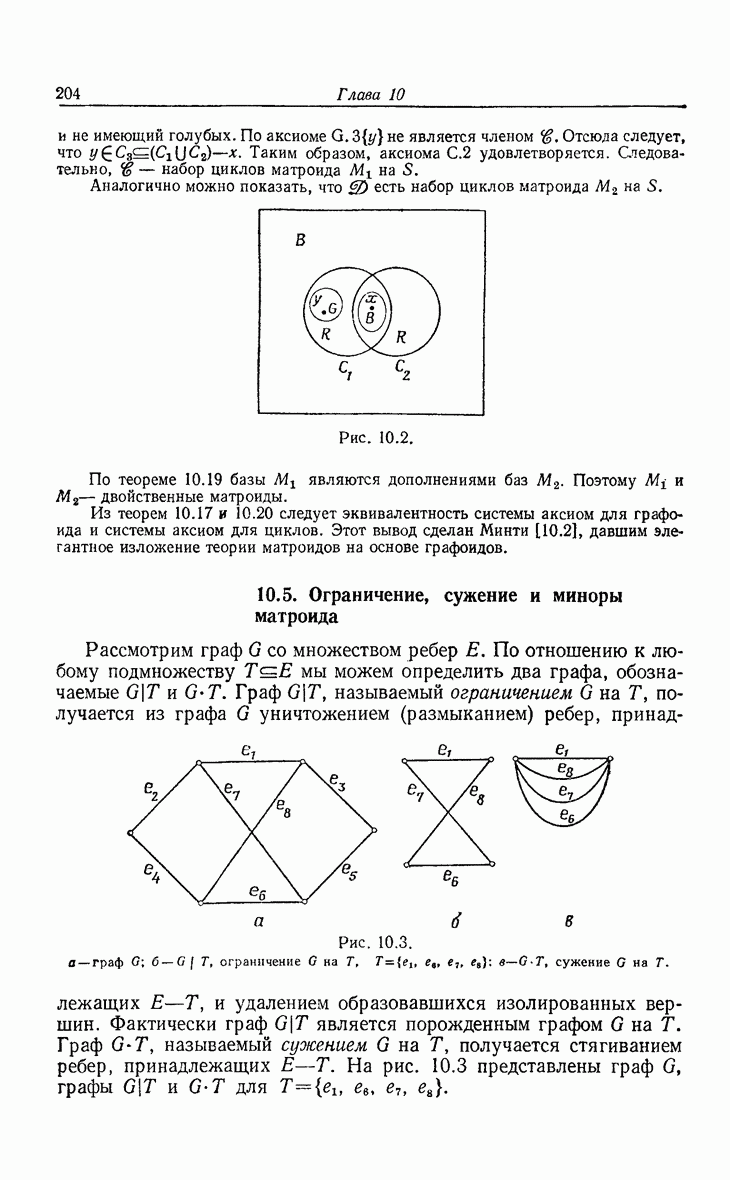
Теорема 10.9. (Аксиомы циклов.) Пусть  — множество циклов матроида на множестве S. Тогда
— множество циклов матроида на множестве S. Тогда  и никакое множество в
и никакое множество в  не содержит другого в качестве собственного подмножества.
не содержит другого в качестве собственного подмножества.
С.2. Если  и то существует такой
и то существует такой  что
что 
Обратно, если набор  подмножеств множества
подмножеств множества  удовлетворяет аксиомам
удовлетворяет аксиомам  то множество
то множество  для всех
для всех  является набором независимых множеств матроида на
является набором независимых множеств матроида на  .
.
Доказательство. Мы уже доказали, что циклы матроида удовлетворяют аксиомам  (теорема 10.4).
(теорема 10.4).
Пусть дан набор  удовлетворяющий аксиомам
удовлетворяющий аксиомам  Покажем, что набор определенный, как в формулировке теоремы, является набором независимых множеств матроида на S. Сделаем это, показывая последовательно, что
Покажем, что набор определенный, как в формулировке теоремы, является набором независимых множеств матроида на S. Сделаем это, показывая последовательно, что  удовлетворяет аксиомам 1.1, 1.2 и 1.3 (теорема 10.6).
удовлетворяет аксиомам 1.1, 1.2 и 1.3 (теорема 10.6).
Заметим сначала, что  есть набор всех подмножеств S, не содержащие ни одного члена
есть набор всех подмножеств S, не содержащие ни одного члена  . Поэтому он удовлетворяет аксиомам 1.1 и 1.2.
. Поэтому он удовлетворяет аксиомам 1.1 и 1.2.
Для доказательства того, что  удовлетворяет аксиоме 1.3, рассмотрим произвольное подмножество
удовлетворяет аксиоме 1.3, рассмотрим произвольное подмножество  . Пусть и
. Пусть и  различные максимальные подмножества А, принадлежащие
различные максимальные подмножества А, принадлежащие  Допуская
Допуская  установим противоречие.
установим противоречие.
Так как  различные подмножества,
различные подмножества,  Пусть
Пусть  Тогда, очевидно, Следовательно, существует
Тогда, очевидно, Следовательно, существует  для которого
для которого  . Более того,
. Более того,  иначе бы
иначе бы  что противоречит принадлежности
что противоречит принадлежности 
Пусть  . Заметим, что
. Заметим, что  Сначала докажем:
Сначала докажем:
1.  . Очевидно, что
. Очевидно, что  Если бы
Если бы  тогда существовал бы такой
тогда существовал бы такой  что
что  Более того,
Более того,  так как
так как  . Таким образом,
. Таким образом,  — такие различные члены что
— такие различные члены что  . Тогда из аксиомы
. Тогда из аксиомы  следует, что существует такой
следует, что существует такой  , что
, что  противоречит тому, что никакой член не содержит членов Следовательно,
противоречит тому, что никакой член не содержит членов Следовательно, 
Теперь докажем:
2. — максимальное подмножество множества А.
Допустим противное. Пусть  такое максимальное подмножество множества А, что
такое максимальное подмножество множества А, что  Теперь
Теперь  так как в противном случае
так как в противном случае  что противоречит максимальности в А. Тогда
что противоречит максимальности в А. Тогда  Следовательно, существует такой
Следовательно, существует такой  Более того,
Более того,  так как иначе бы
так как иначе бы  Пусть
Пусть  Тогда можно показать (как в доказательстве п. 1), что
Тогда можно показать (как в доказательстве п. 1), что  что противоречит максимальности
что противоречит максимальности  в А. Таким образом,
в А. Таким образом,  — максимальное подмножество в А.
— максимальное подмножество в А.
Заметим, что  построено из заменой элемента
построено из заменой элемента  на элемент
на элемент  Поскольку
Поскольку  мы можем повторить эту конструкцию конечное число раз, получив максимальное такое подмножество
мы можем повторить эту конструкцию конечное число раз, получив максимальное такое подмножество  , что
, что  что противоречит равенству
что противоречит равенству  . Поэтому существует такой элемент
. Поэтому существует такой элемент  что
что  . Поэтому существует такой элемент
. Поэтому существует такой элемент  что
что  и аксиома 1.3, таким образом, удовлетворяется,
и аксиома 1.3, таким образом, удовлетворяется,
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Часть I. Теория графов
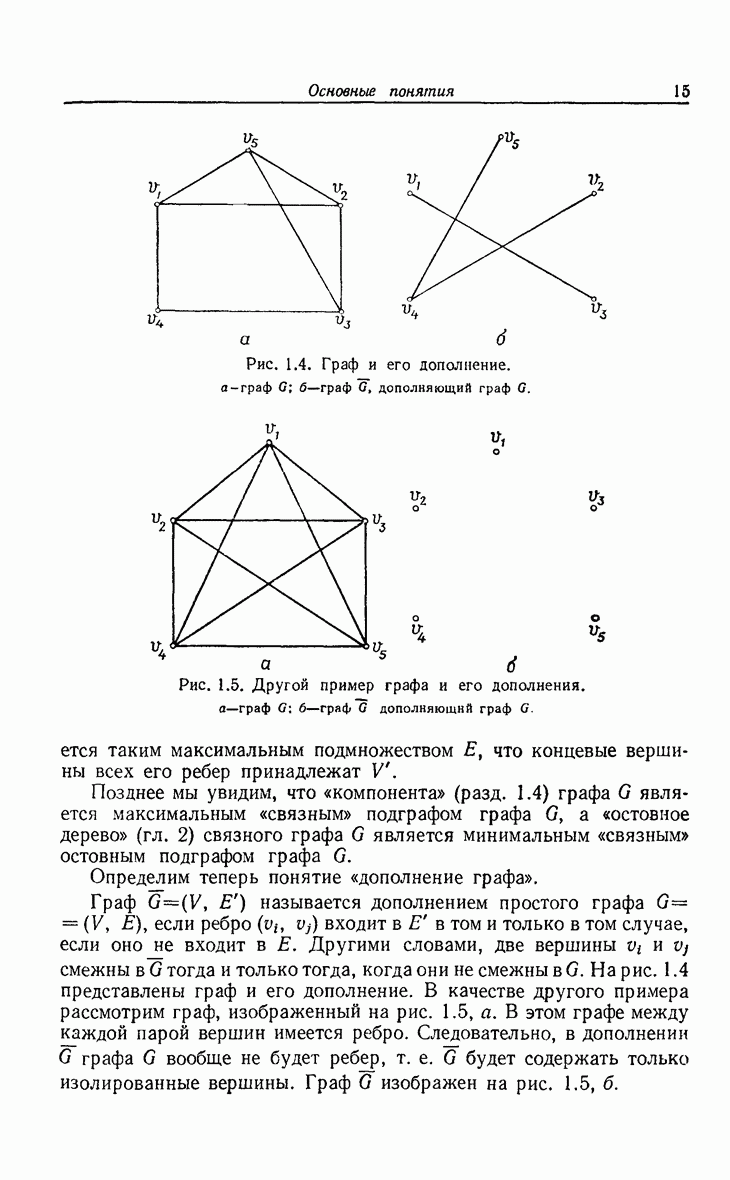
- 1.2. Подграфы и дополнения
- 1.3. Маршруты, цепи, пути и циклы
- 1.4. Связность и компоненты графа
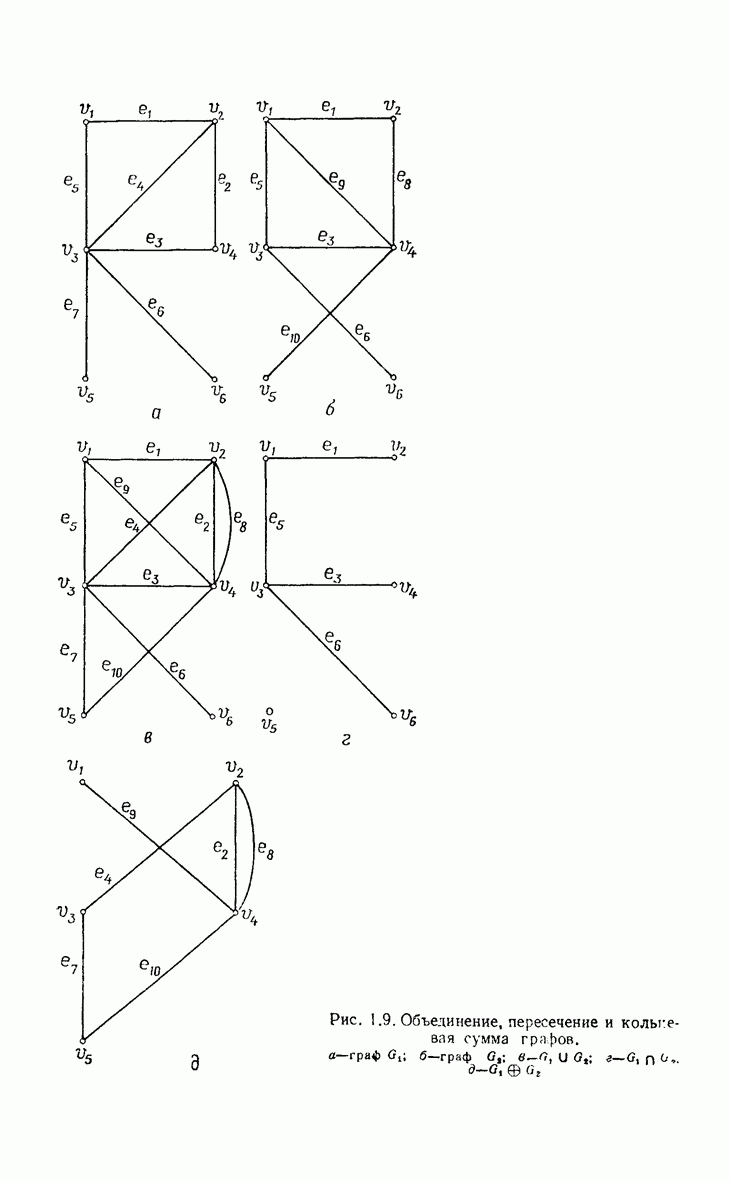
- 1.5. Операции над графами
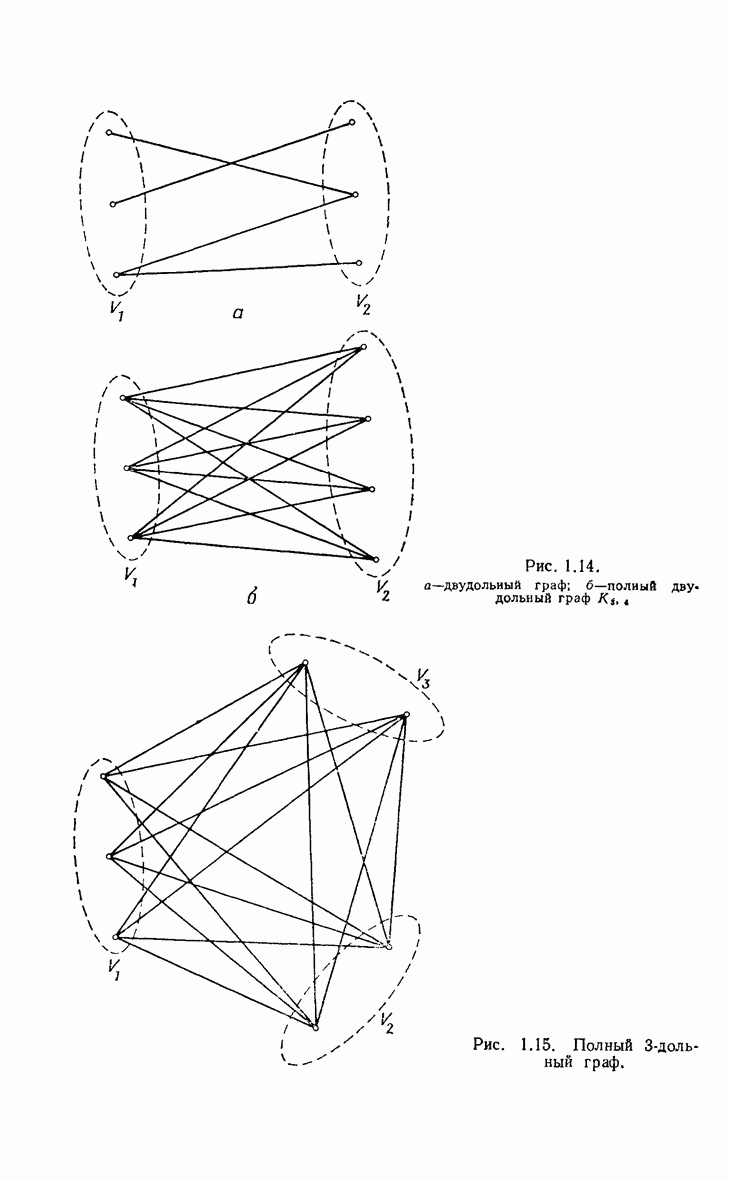
- 1.6. Специальные графы
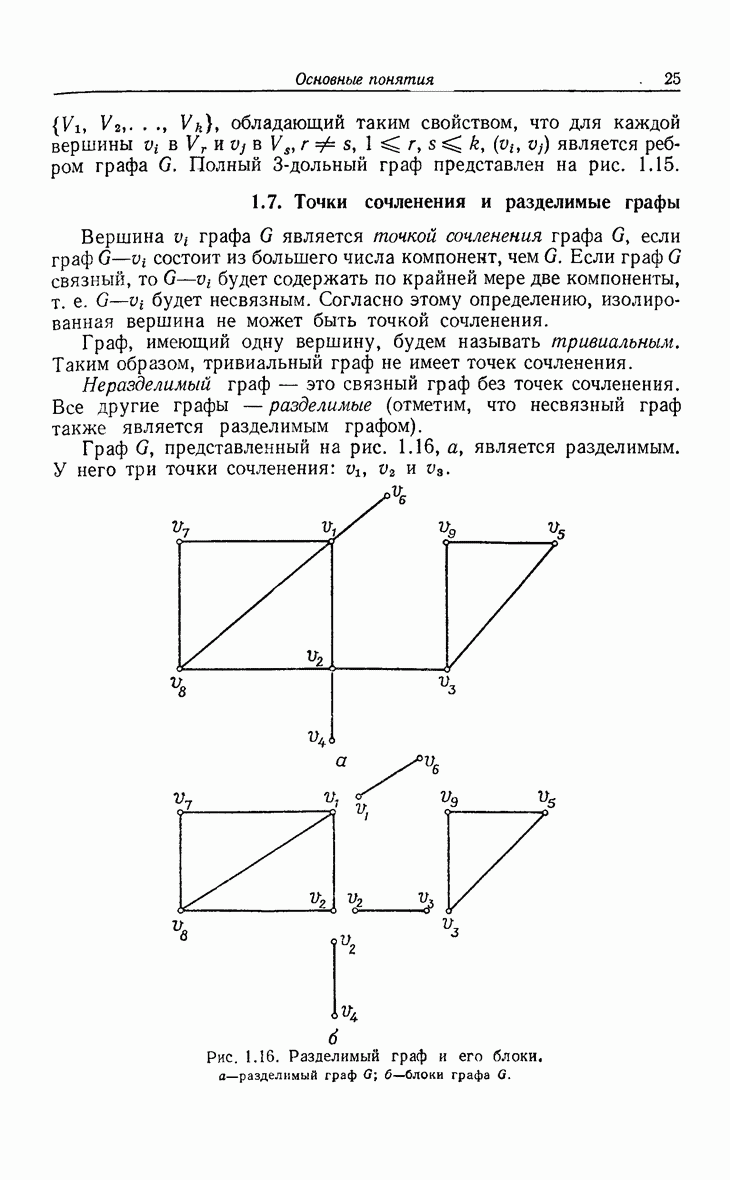
- 1.7. Точки сочленения и разделимые графы
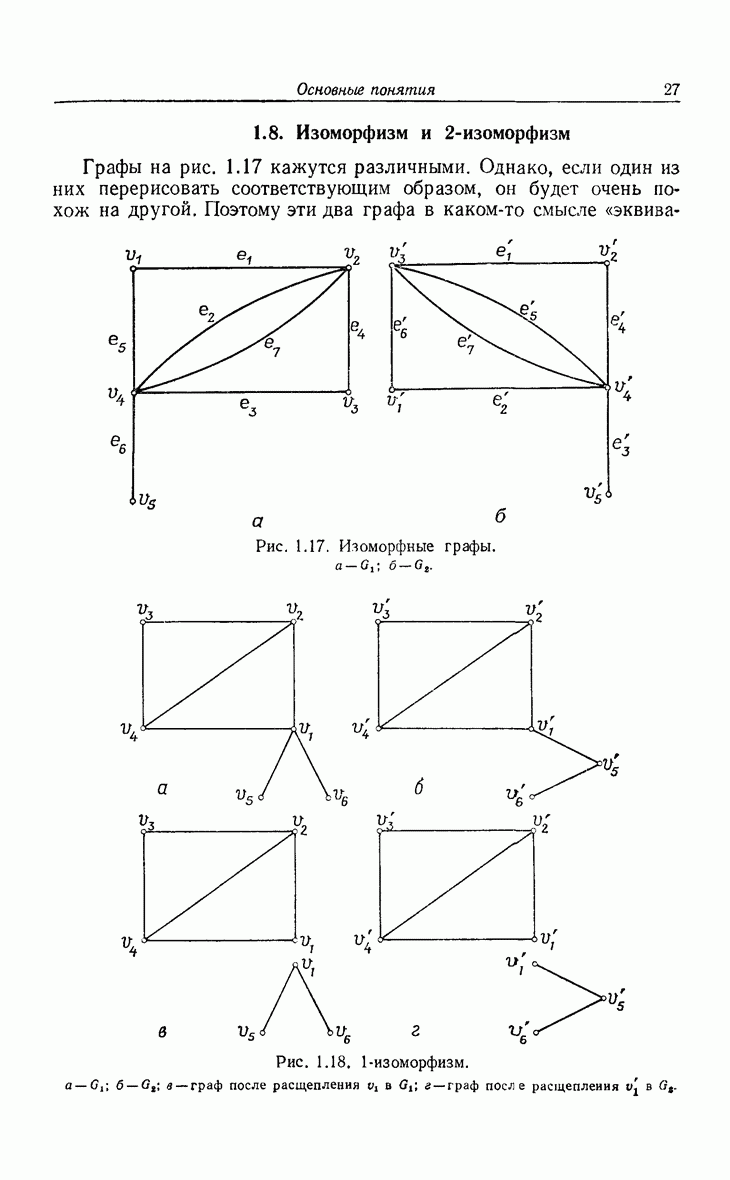
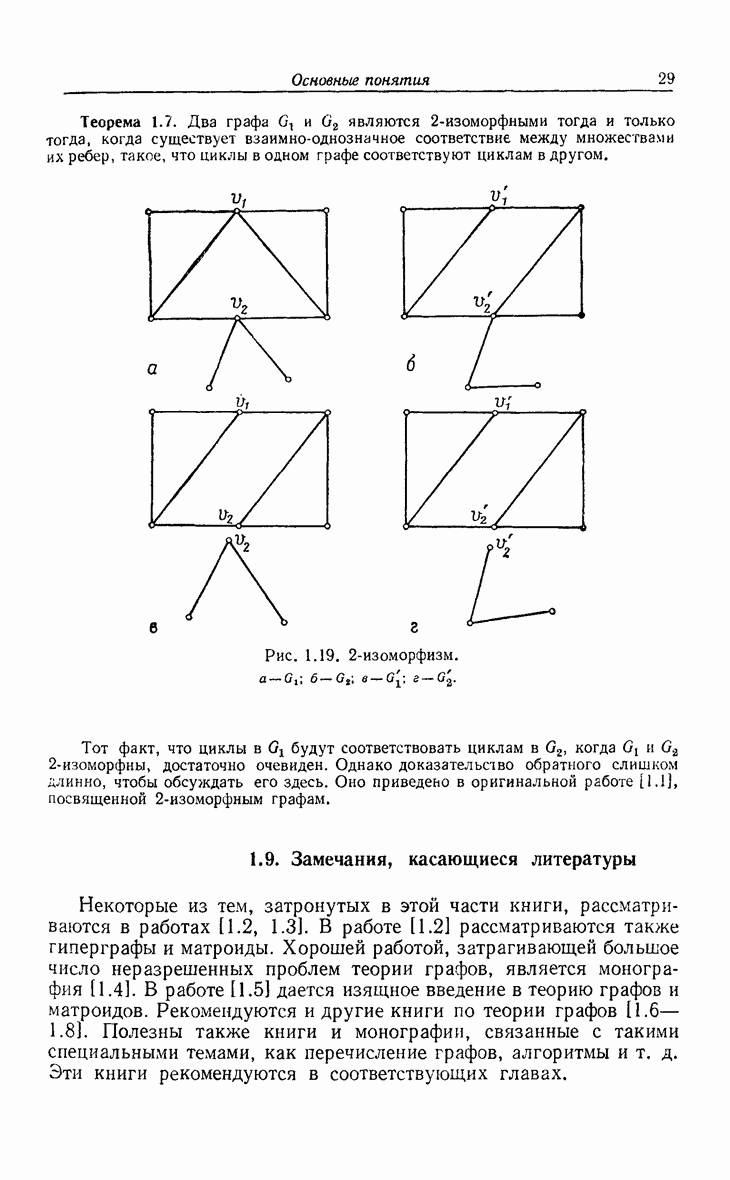
- 1.8. Изоморфизм и 2-изоморфизм
- 1.9. Замечания, касающиеся литературы
- Упражнения
- 2. Деревья, разрезающие множества и циклы
- 2.1. Деревья, остовы и кодеревья
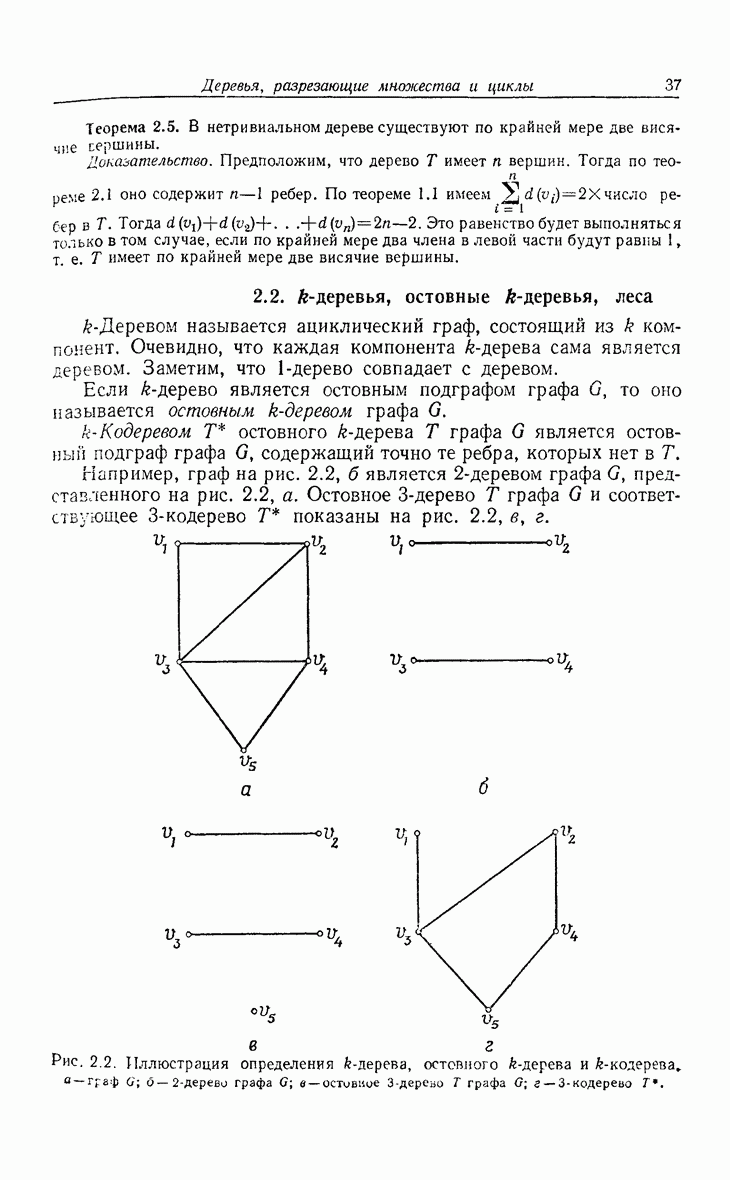
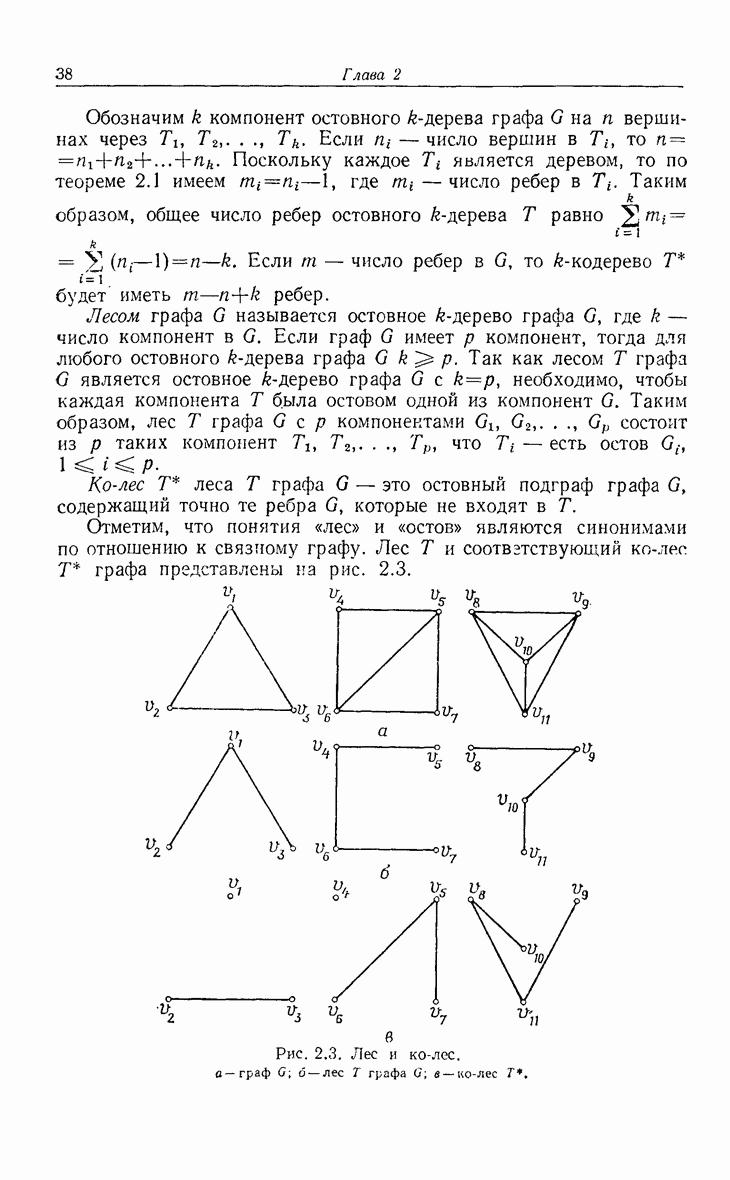
- 2.2. k-деревья, остовные k-деревья, леса
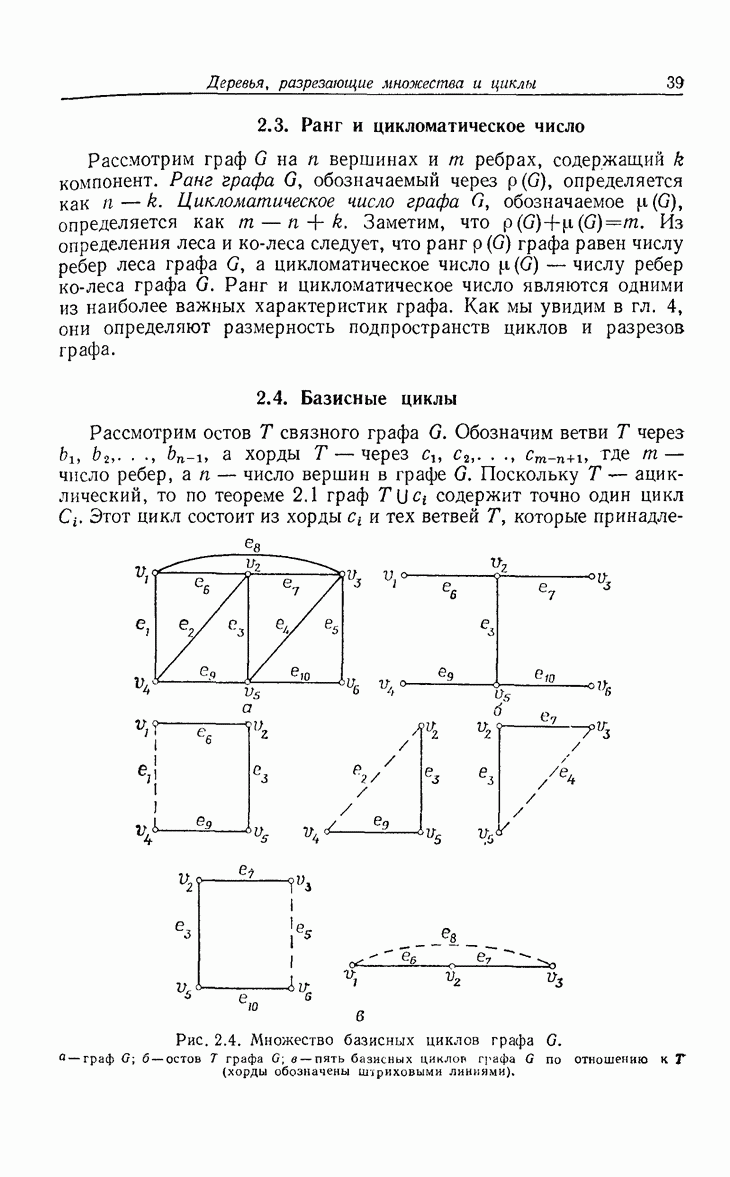
- 2.4. Базисные циклы
- 2.5. Разрезающие множества
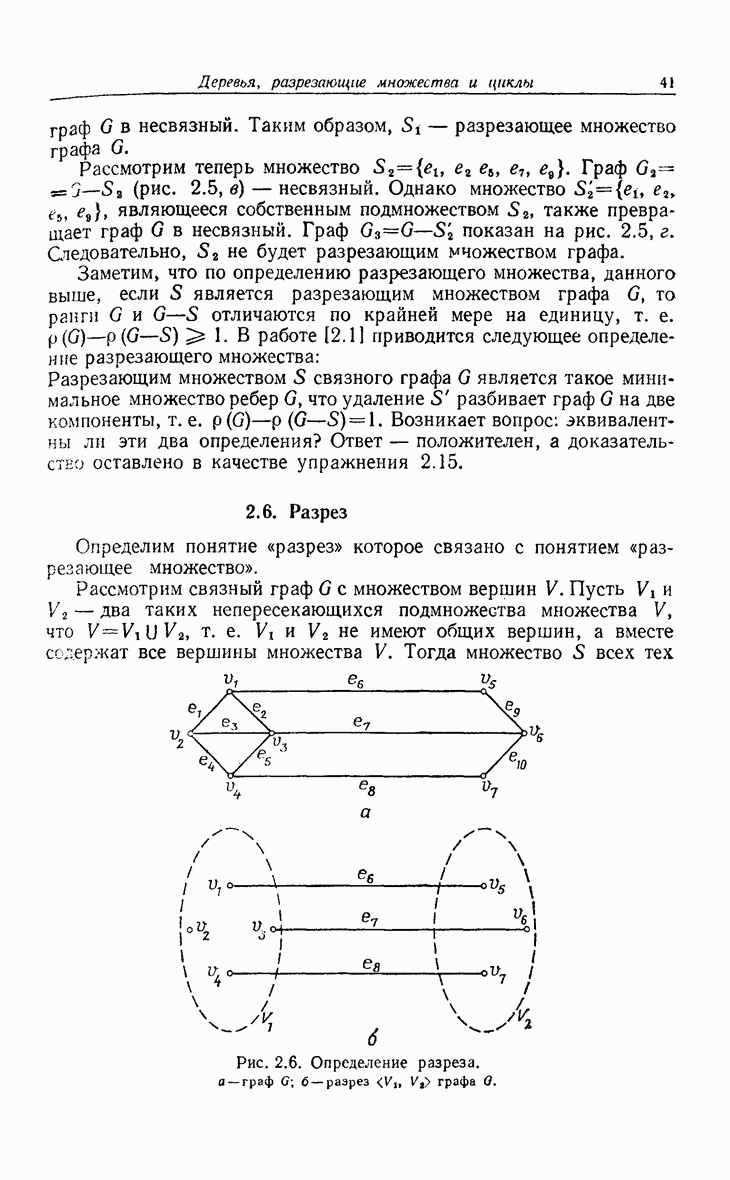
- 2.6. Разрез
- 2.7. Базисные разрезающие множества
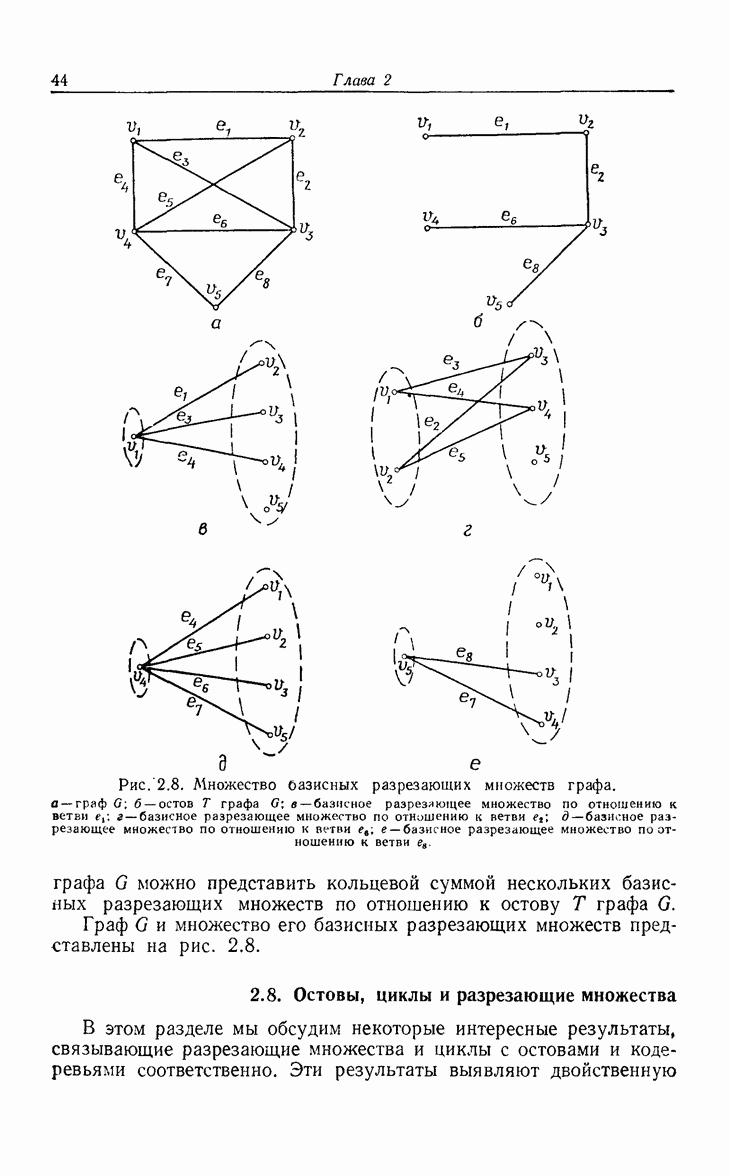
- 2.8. Остовы, циклы и разрезающие множества
- 2.9. Замечения, касающиеся литературы
- Упражнения
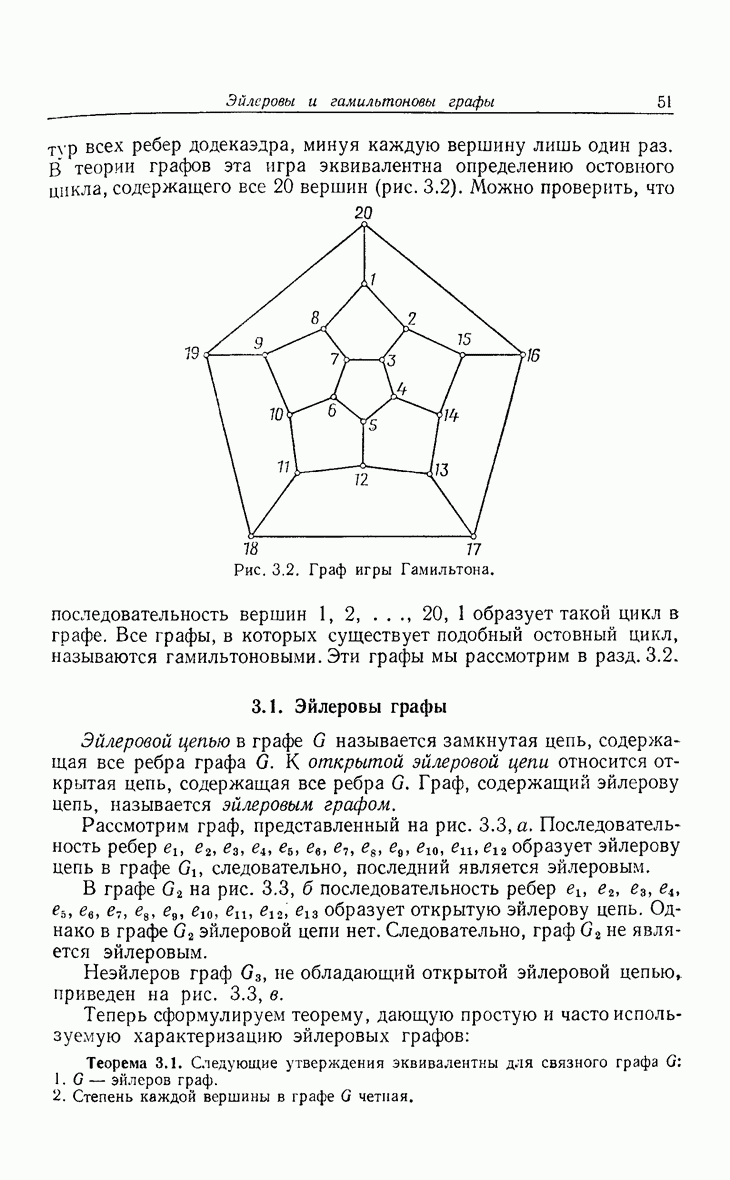
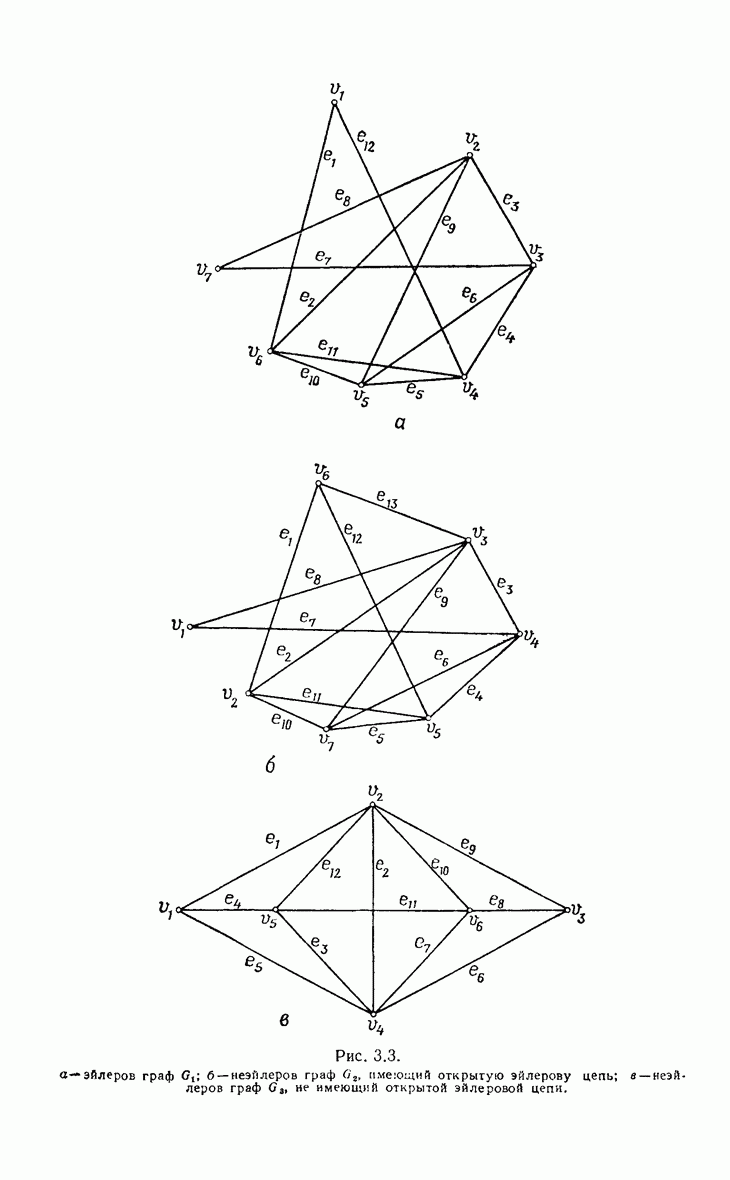
- 3. Эйлеровы и гамильтоновы графы
- 3.1. Эйлеровы графы
- 3.2. Гамильтоновы графы
- 3.3. Замечания, касающиеся литературы
- Упражнения
- 4. Графы и векторные пространства
- 4.2. Векторные пространства
- 4.3. Векторное пространство графа
- 4.4. Размерность подпространств циклов и разрезов
- 4.5. Связь между подпространствами циклов и разрезов
- 4.6. Ортогональность подпространств циклов и разрезов
- 4.7. Замечания, касающиеся литературы
- Упражнения
- 5. Ориентированные графы
- 5.2. Графы и отношения
- 5.3. Ориентированные или корневые деревья
- 5.4. Ориентированные эйлеровы графы
- 5.5. Ориентированные остовы и ориентированные эйлеровы цепи
- 5.6. Ориентированные гамильтоновы графы
- 5.7. Ациклические ориентированные графы
- 5.8. Турниры
- 5.9. Замечания, касающиеся литературы
- Упражнения
- 6. Матрицы графов
- 6.2. Матрица разрезов
- 6.3. Цикломатическая матрица
- 6.4. Соотношение ортогональности
- 6.5. Подматрицы матриц разрезов, инциденций и циклов
- 6.6. Унимодулярные матрицы
- 6.7. Число остовов
- 6.8 Число остовных 2-деревьев
- 6.9 Число ориентированных остовов в ориентированном графе
- 6.10. Матрица смежности
- 6.11. Графы Коутса и Мэзона
- 6.12. Замечания, касающиеся литературы
- Упражнения
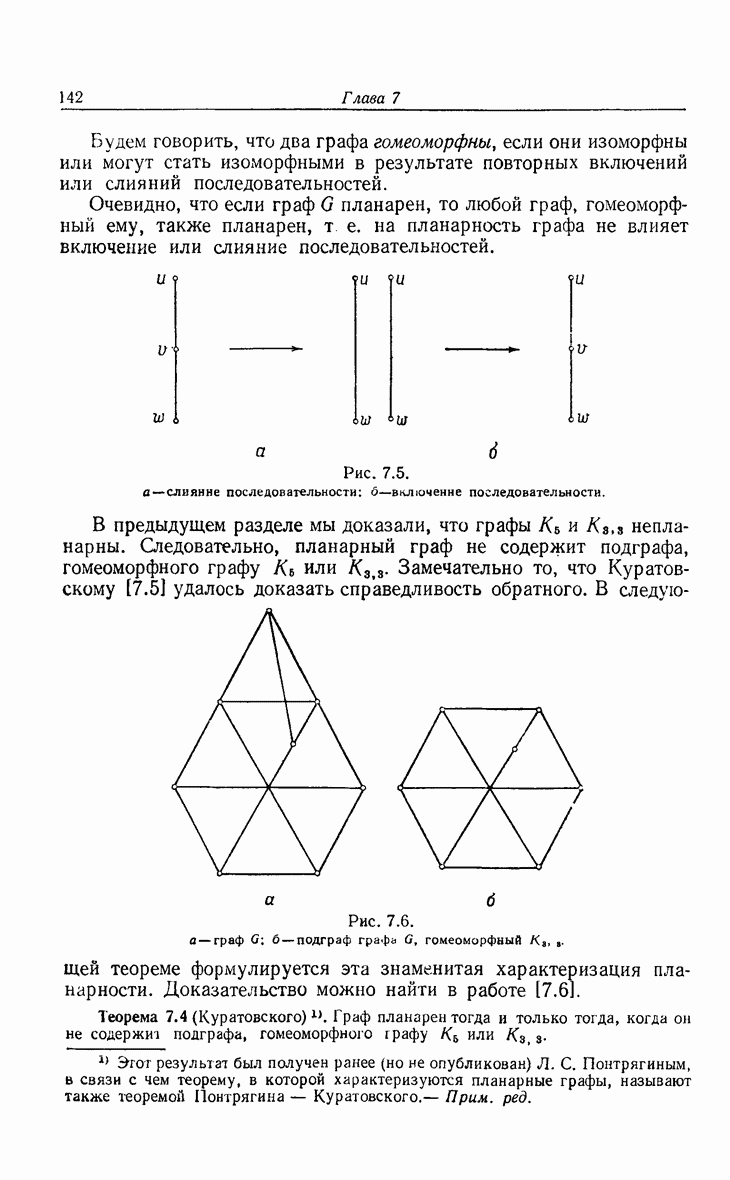
- 7. Планарность и двойственность
- 7.2. Формула Эйлера
- 7.3. Теорема Куратовского и другие характеризации планарности
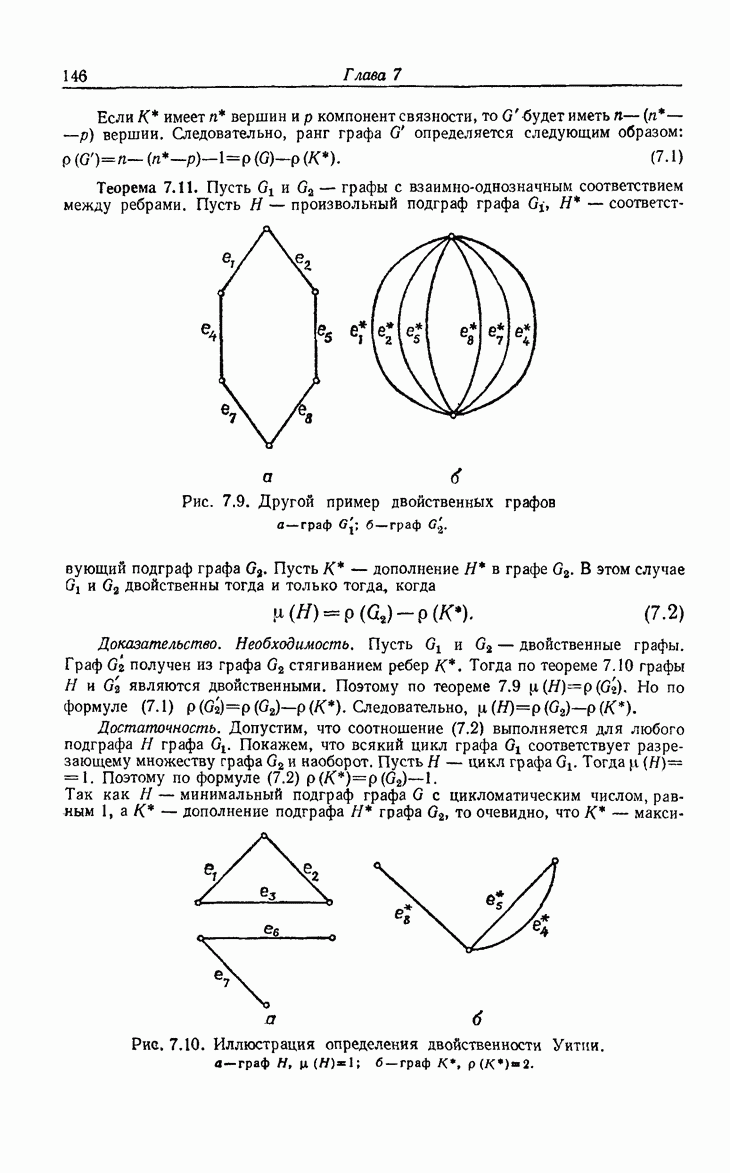
- 7.4. Двойственные графы
- 7.5. Планарность и двойственность
- 7.6. Замечания, касающиеся литературы
- Упражнения
- 8. Связность и паросочетания
- 8.2. Реберная связность
- 8.3. Графы с заданными степенями
- 8.4. Теорема Менгера
- 8.5. Паросочетания
- 8.6. Паросочетания в двудольных графах
- 8.7. Паросочетания графов общего вида
- 8.8. Замечания, касающиеся литературы
- Упражнения
- 9. Покрытия и раскраски
- 9.1. Независимые множества и вершинные покрытия
- 9.2. Реберные покрытия
- 9.3. Реберная раскраска и хроматический индекс
- 9.4. Вершинная раскраска и хроматическое число
- 9.5. Хроматические полиномы
- 9.6. Проблема четырех красок
- 9.7. Замечания, касающиеся литературы
- Упражнения
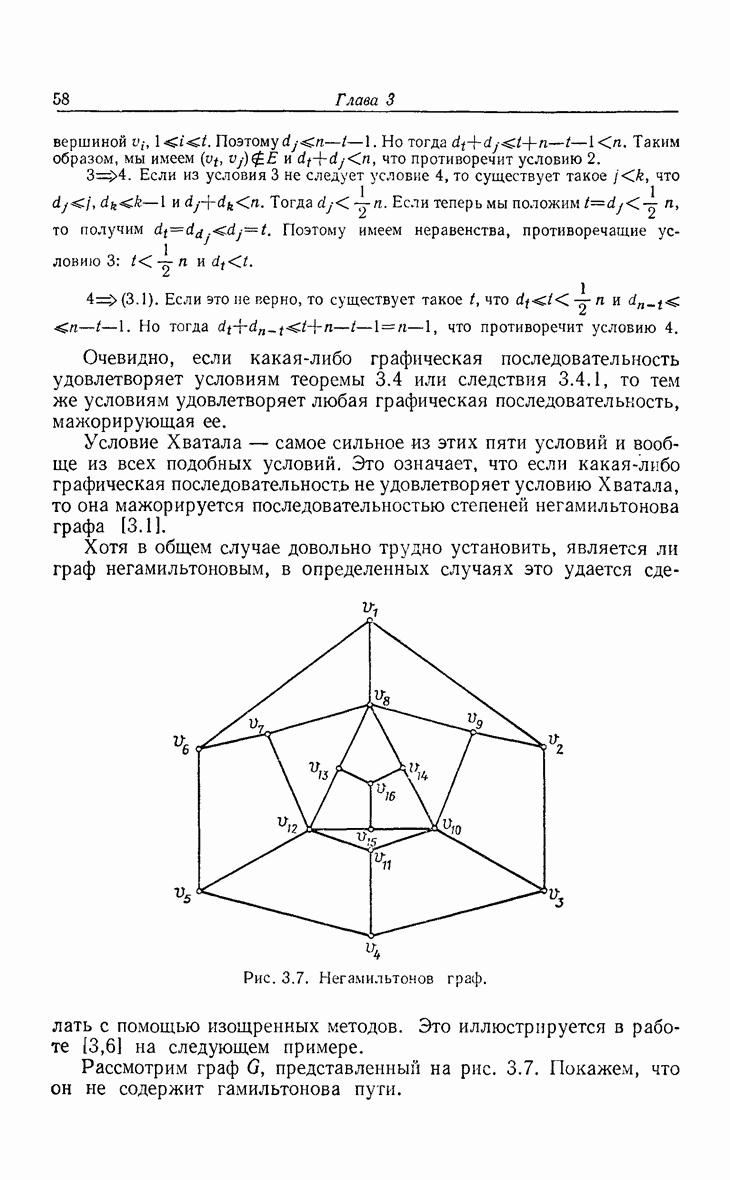
- 10. Матроиды
- 10.2. Фундаментальные свойства
- 10.3. Эквивалентные системы аксиом
- 10.4. Двойственность матроидов и графоиды
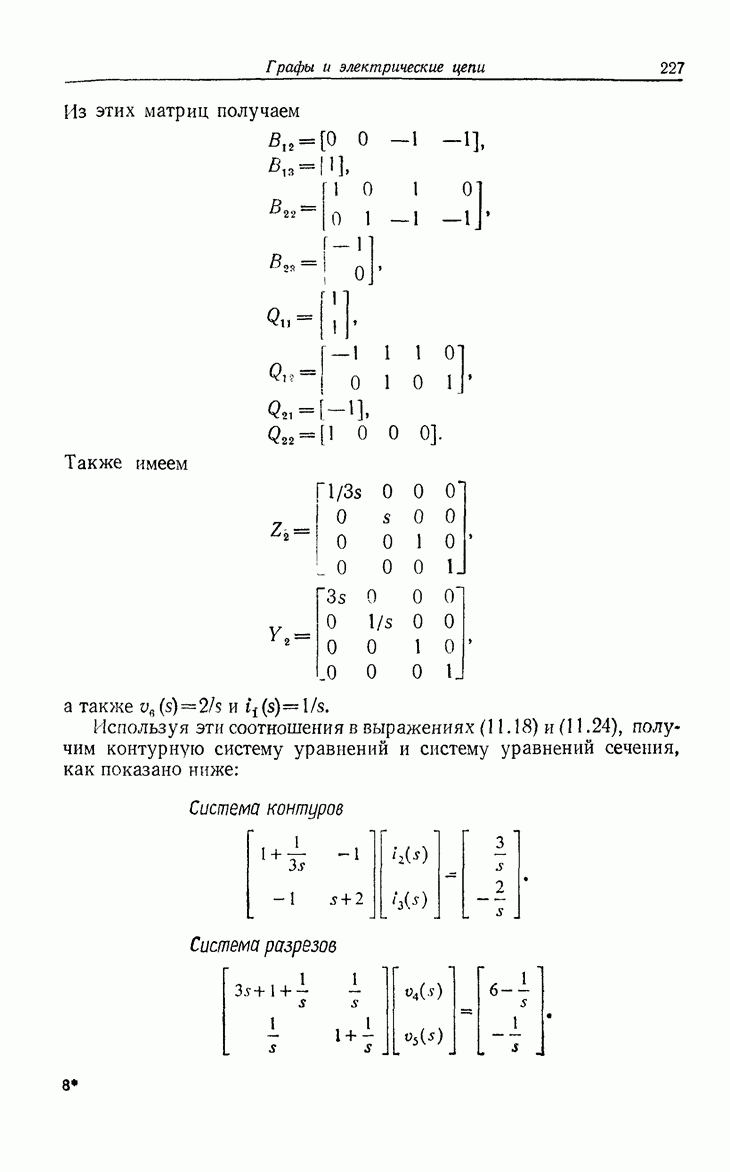
- 10.5. Ограничение, сужение и миноры матроида
- 10.6. Представимость матроидов
- 10.7. Бинарные матроиды
- 10.8. Ориентируемые матроиды
- 10.9. Матроиды и «жадный» алгоритм
- 10.10. Замечания, касающиеся литературы
- Упражнения
- Часть II. Теория электрических цепей
- 11. Графы и электрические цепи
- 11.1. Преобразование контуров и сечений
- 11.2. Системы контурных уравнений и уравнений сечений
- 11.3. Метод смешанных переменных
- 11.4. Главное разбиение графа
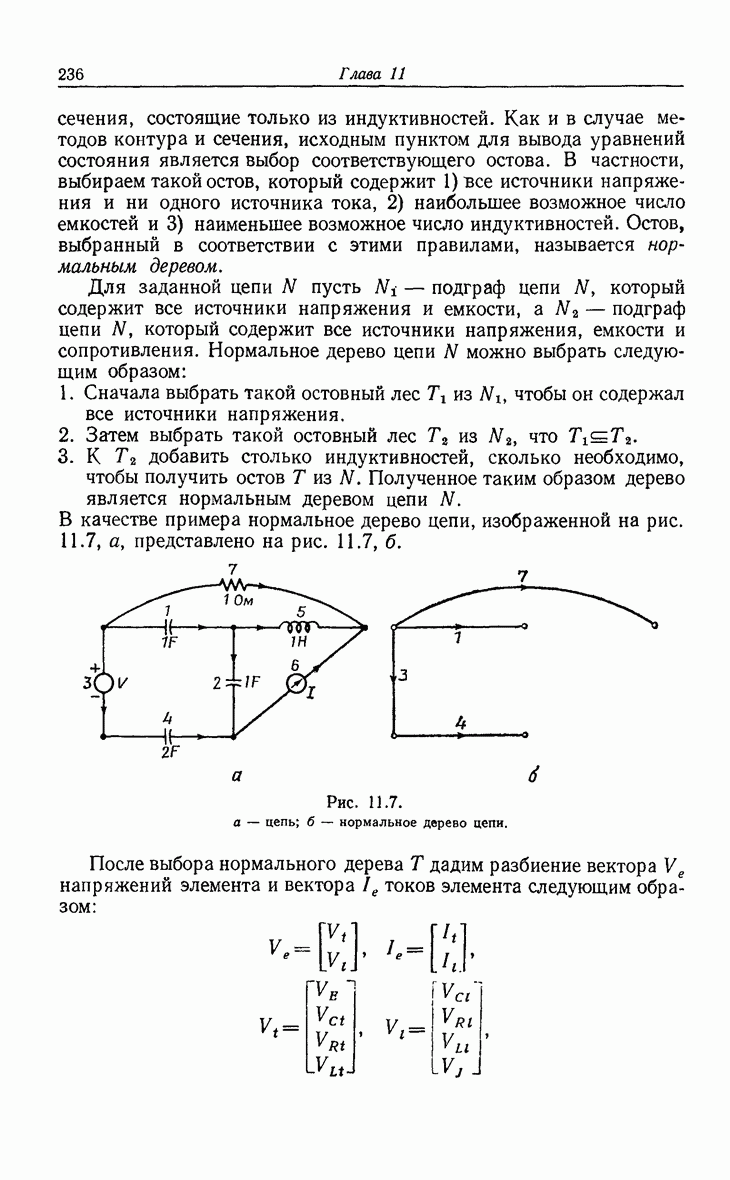
- 11.5. Уравнения состояния
- 11.6. Свойство неусиления в резистивных цепях
- 11.7. Замечания, касающиеся литературы
- Упражнения
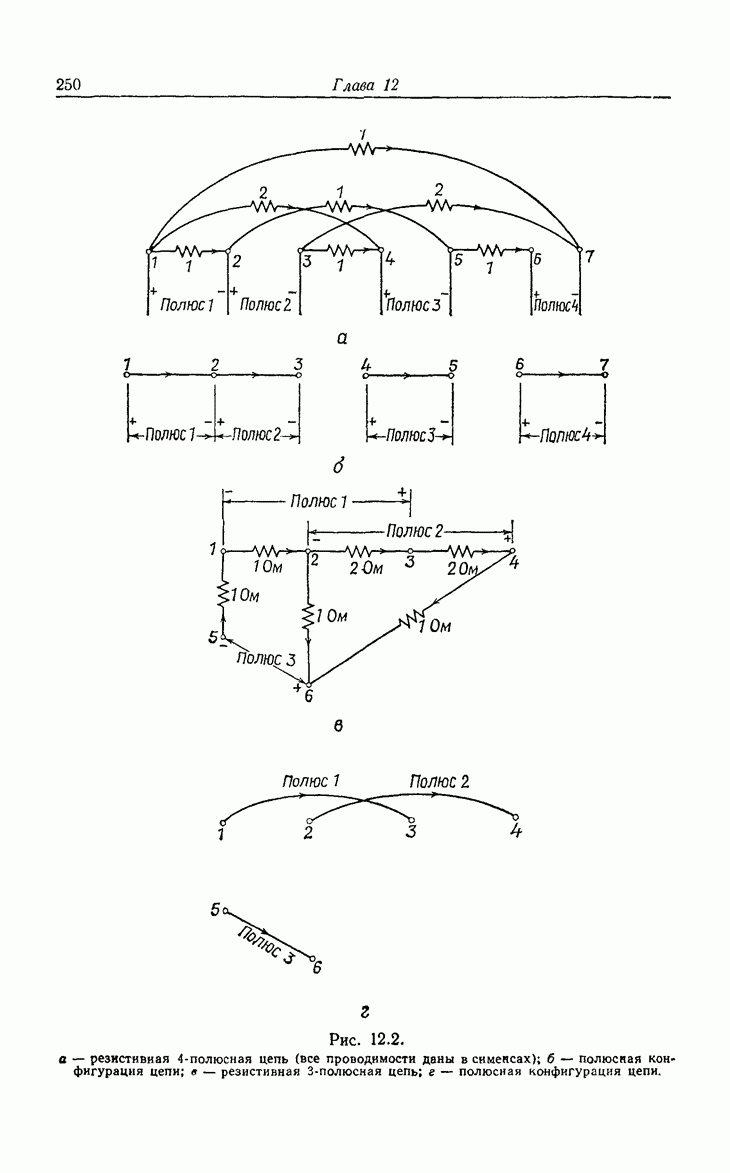
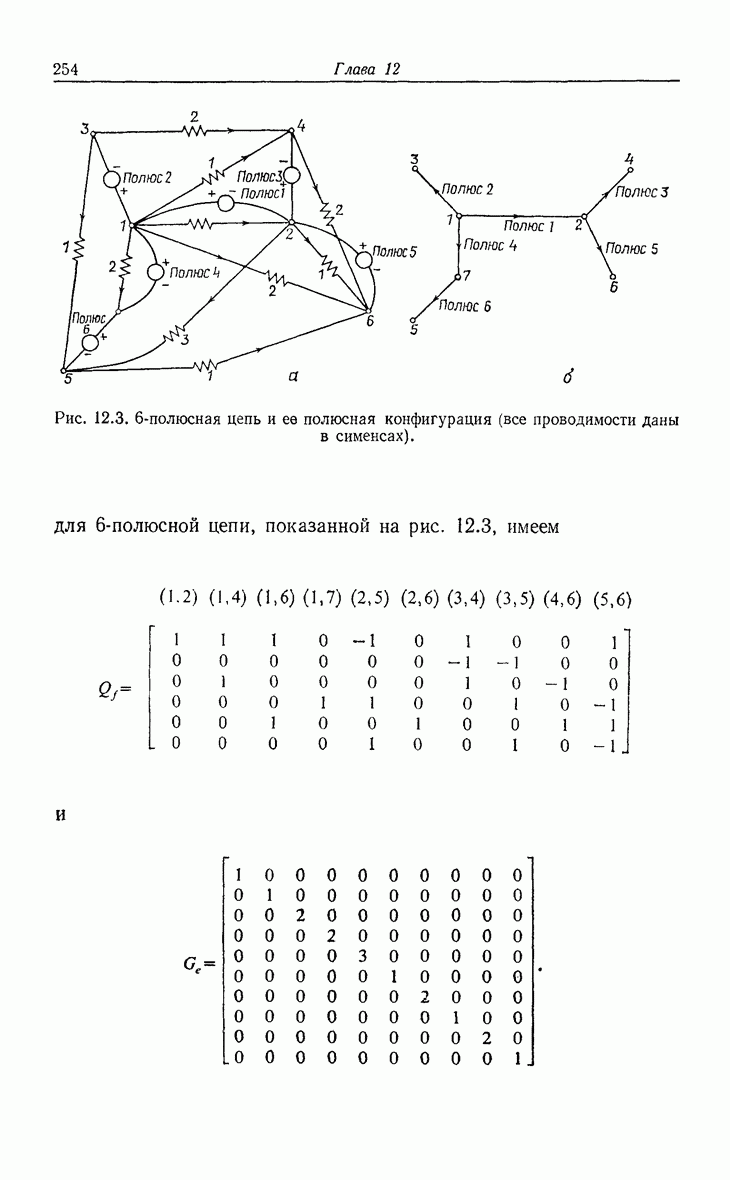
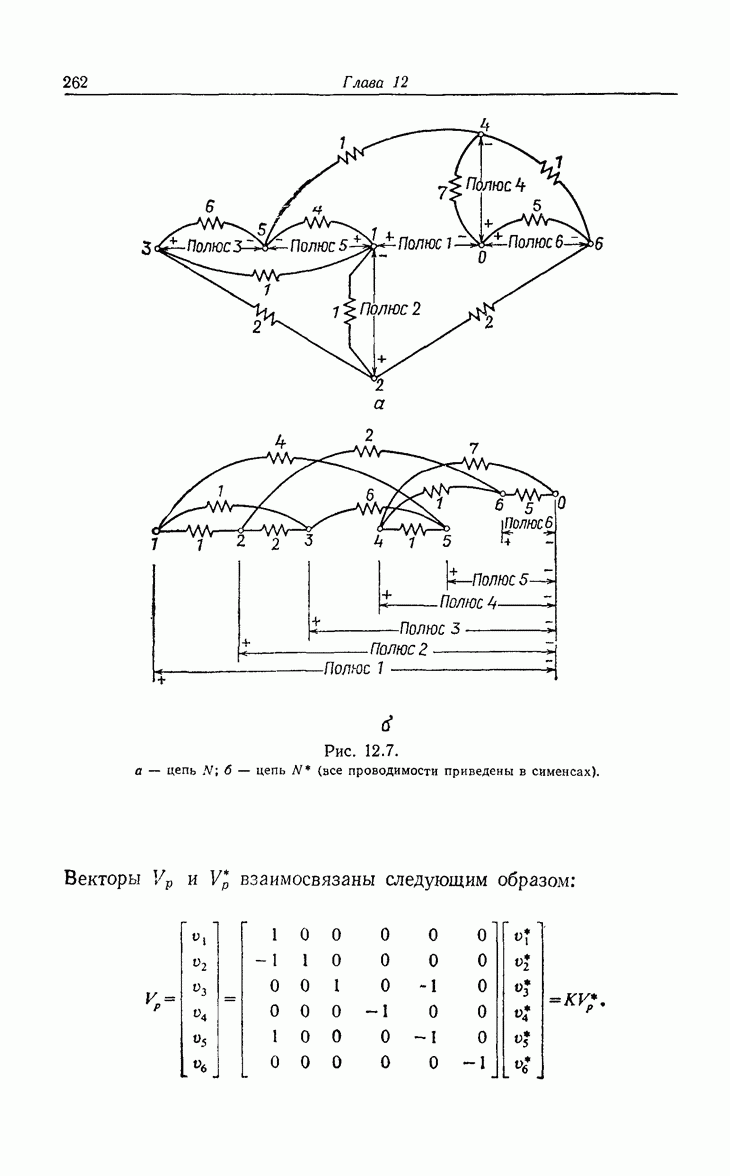
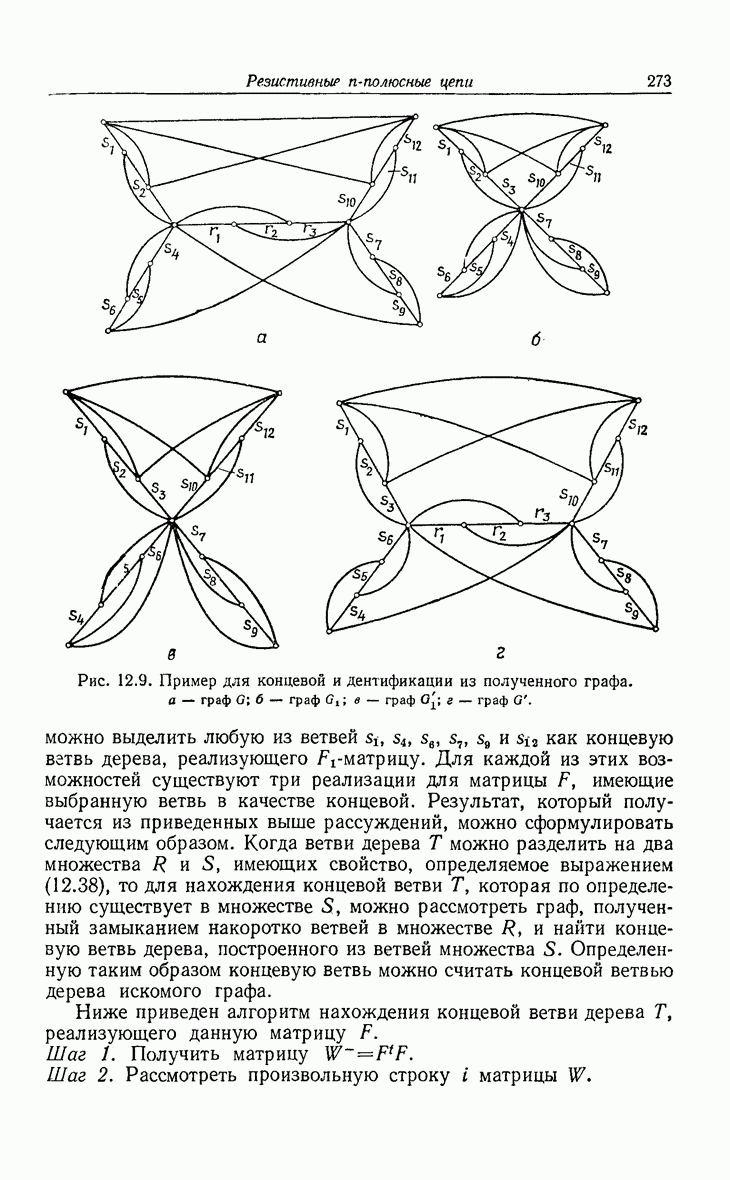
- 12. Резистивные n-полюсные цепи
- 12.2. K-матрицы резистивной (n-полюсной цепи ранга n)
- 12.3. Реализация (n+1)-узловых резистивных n-полюсных цепей (подход Седербаума)
- 12.4. Реализация цикломатической матрицы и матрицы сечений
- 12.5. Реализация (n+1)-узловых резистивных n-полюсных цепей (подход Гуиллемина)
- 12.6. Замечания, касающиеся литературы
- Упражнения
- 13. Функции цепи и чувствительность цепи
- 13.1. Топологические формулы для RLC-цепей без взаимных индуктивностей
- 13.2. Топологические формулы для общих линейных цепей
- 13.3. Сопряженная цепь и вычисление чувствительности цепи
- 13.4. Замечания, касающиеся литературы
- Упражнения
- Часть III. Теория электрических цепей
- 14. Алгоритмы анализа графов
- 14.1. Транзитивное замыкание
- 14.2. Транзитивная ориентация
- 14.3. Поиск в глубину
- 14.4. Двусвязность и сильная связность
- 14.6. Доминаторы в графе программы
- 14.7. Замечания, касающиеся литературы
- Упражнения
- 15. Оптимизационные алгоритмы
- 15.2. Деревья с минимальной длиной взвешенных путей.
- 15.3. Оптимальные деревья бинарного поиска
- 15.4. Максимальные паросочетания в графе
- 15.5. Максимальные паросочетания в двудольном графе
- 15.6. Совершенное паросочетание, оптимальное назначение и составление расписаний
- 15.7. Потоки в транспортной сети
- 15.8. Оптимальное ветвление
- 15.9. Замечания, касающиеся литературы
- Упражнения
- ЛИТЕРАТУРА