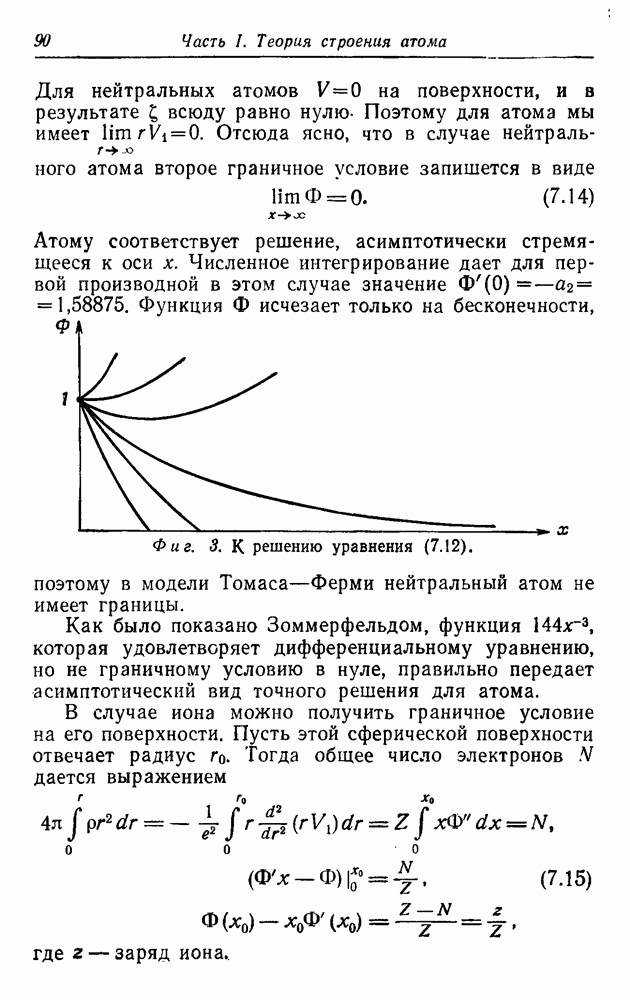
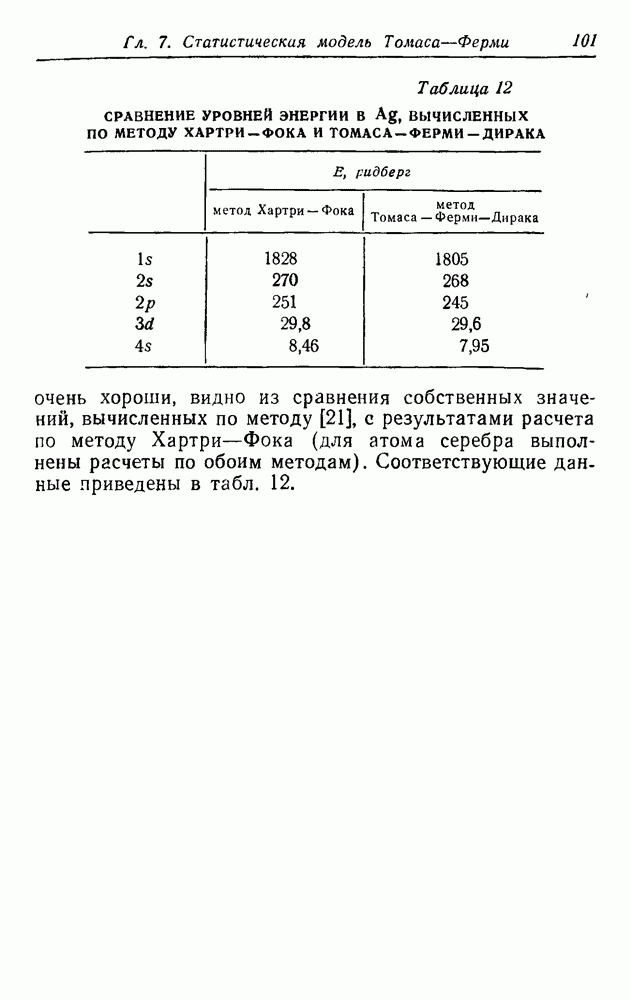
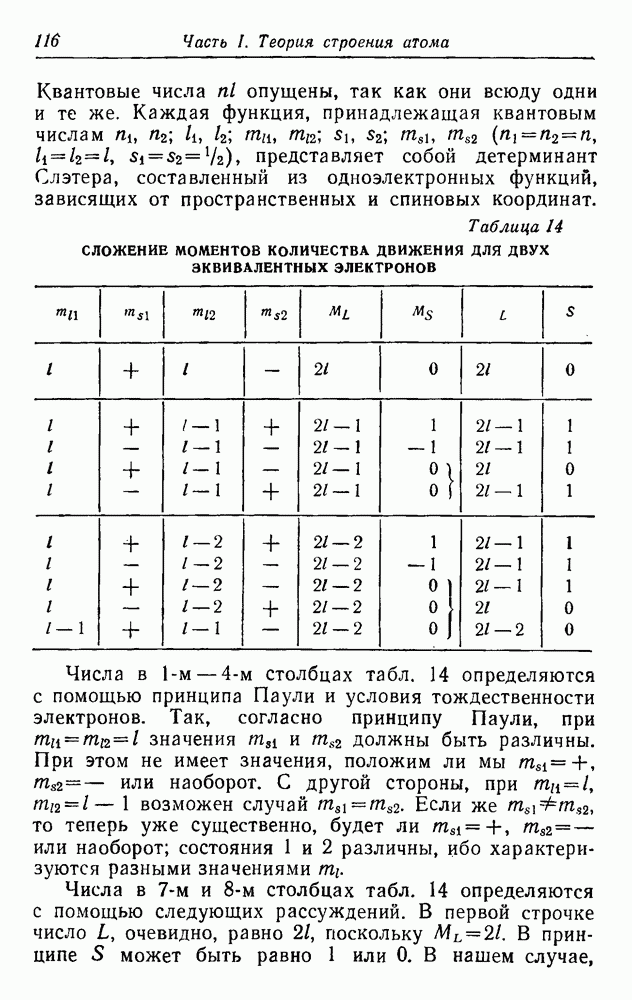
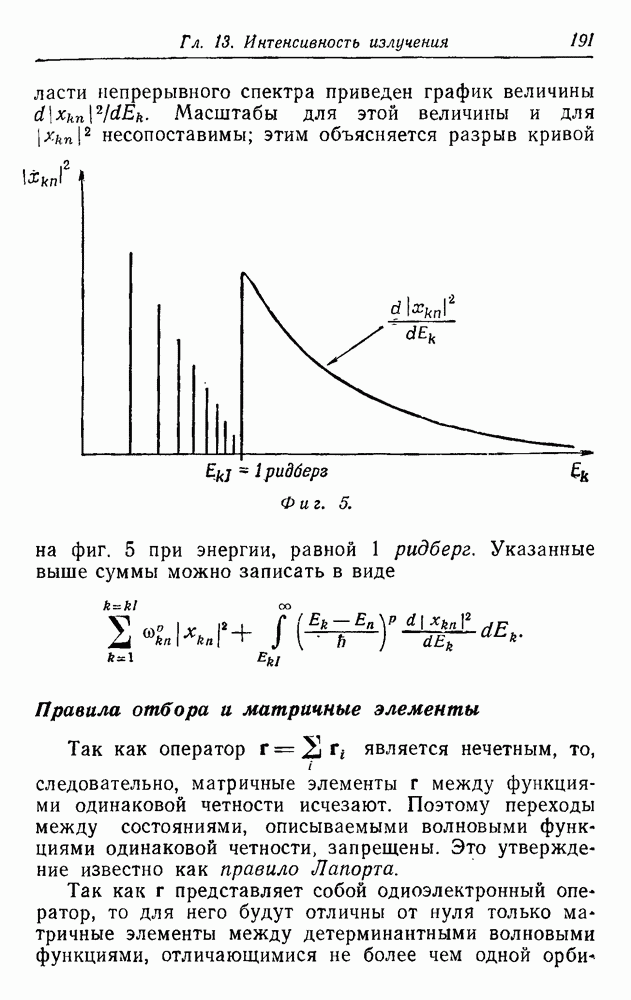
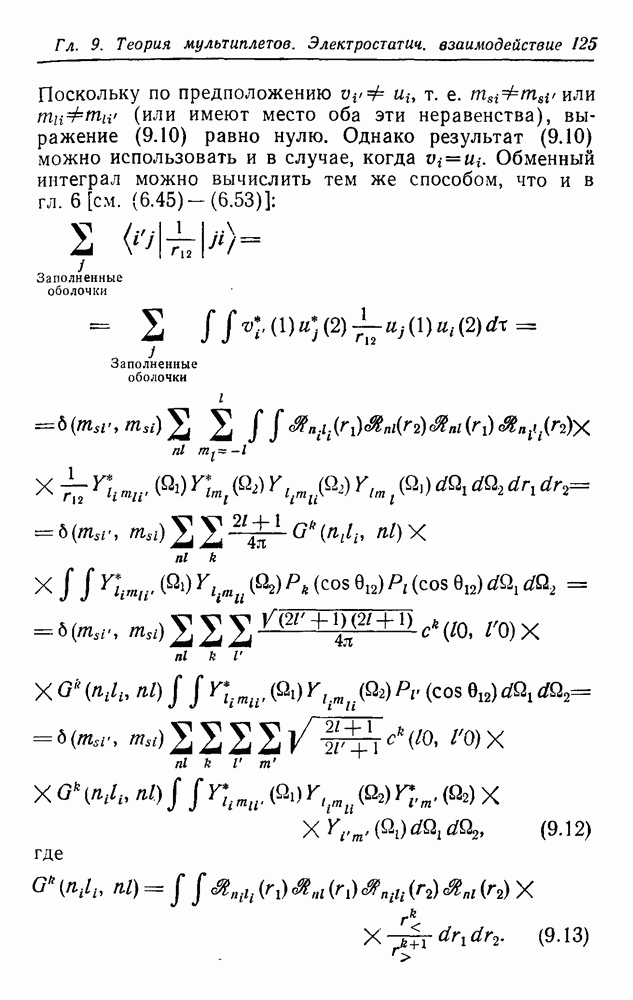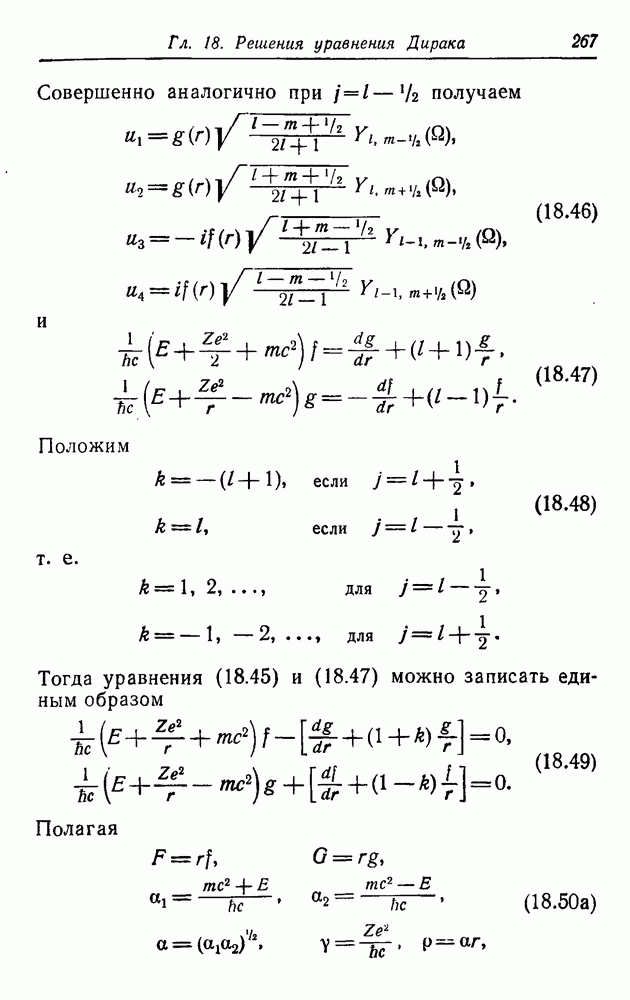| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
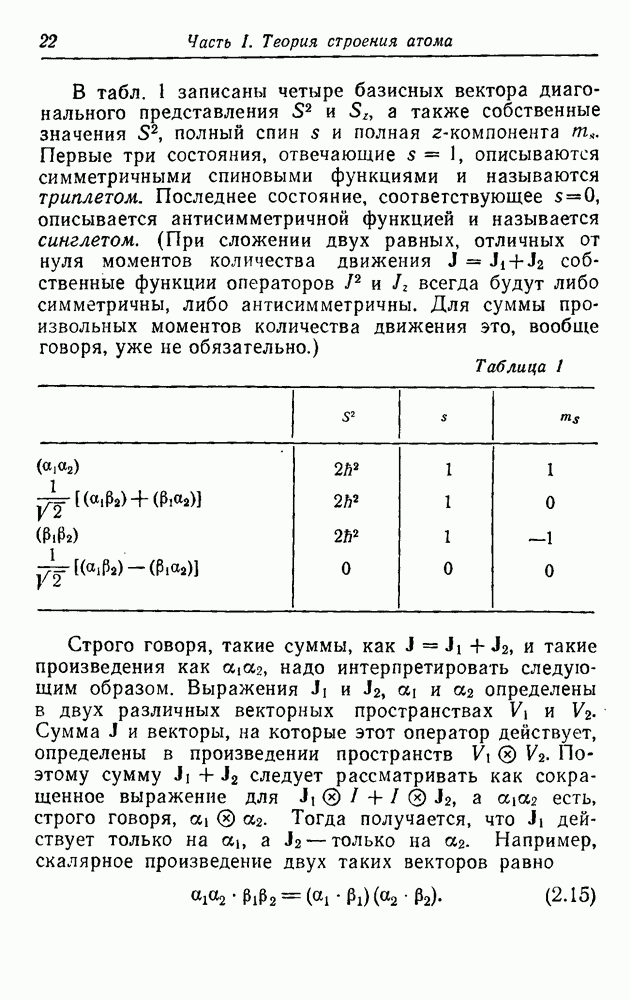
9. ТЕОРИЯ МУЛЬТИПЛЕТОВ. ЭЛЕКТРОСТАТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ
Придерживаясь программы, намеченной в начале гл. 8, вычислим теперь матричные элементы гамильтониана Н в представлении, в котором матрицы  диагональны. Речь идет о вычислении выражений вида
диагональны. Речь идет о вычислении выражений вида

Каждая волновая функция, стоящая в обкладках матричного элемента, есть суперпозиция детерминантных волновых функций для данной электронной конфигурации

Матричный элемент гамильтониана равен

Здесь каждая волновая функция в обкладке есть детерминант Слэтера. Каждый из индексов  и k указывает на определенный набор значений
и k указывает на определенный набор значений  для электронов в незаполненной оболочке (или оболочках); каждый такой набор определяет детерминант Слэтера. Суммирование производится по всем возможным наборам
для электронов в незаполненной оболочке (или оболочках); каждый такой набор определяет детерминант Слэтера. Суммирование производится по всем возможным наборам  и k. Предполагается, что в незаполненной оболочке (или оболочках) находятся
и k. Предполагается, что в незаполненной оболочке (или оболочках) находятся  электронов.
электронов.
Вычисление матричных элементов
Таким образом, мы пришли к рассмотрению Матричных элементов гамильтониана Н между состояниями, задаваемыми детерминантными волновыми функциями.
Поскольку

где  — оператор, изменяющий состояние только одного электрона,
— оператор, изменяющий состояние только одного электрона,  — оператор, изменяющий состояние двух электронов, соответствующие матричные элементы даются формулами (6.13) — (6.18). Рассмотрим сначала одноэлектронный оператор
— оператор, изменяющий состояние двух электронов, соответствующие матричные элементы даются формулами (6.13) — (6.18). Рассмотрим сначала одноэлектронный оператор

В соответствии с формулами (6.13) и (6.14) отличный от нуля вклад в сумму (9.3) может получиться только в двух случаях: 1) начальный и конечный детерминанты отличаются одной орбиталью, 2) все орбитали в них одинаковы. В первом случае вклад все же равен нулю по следующей причине. Пусть в начальном и конечном детерминантах различны  орбитали. Вычислим интеграл
орбитали. Вычислим интеграл

в котором

Поскольку состояния  различаются только заданием чисел
различаются только заданием чисел  или
или  интегрирования по
интегрирования по  или по спиновому пространству в (6.13) обращают интеграл в нуль.
или по спиновому пространству в (6.13) обращают интеграл в нуль.
Вклад диагональных элементов

как видно из выражения (9.5), не зависит от значений  Мы имеем
Мы имеем

где суммирование по i производится по всем заполненным состояниям с квантовыми числами  члене. Из выражения (9.5) следует, что матричный элемент
члене. Из выражения (9.5) следует, что матричный элемент  зависит только от
зависит только от  и не зависит от
и не зависит от  поскольку интеграл по углам равен единице:
поскольку интеграл по углам равен единице:

Поэтому сумма по i в (9.6) одна и та же для всех детерминантов Слэтера  возможных при данной электронной конфигурации. Итак,
возможных при данной электронной конфигурации. Итак,

для любой волновой функции типа (9.2). Поскольку в конечном счете нас будут интересовать разности членов с различными  или
или  вклад
вклад  в среднее значение (Н) можно вообще опустить.
в среднее значение (Н) можно вообще опустить.
Вычислим теперь величину  . Согласно формулам (6.15), (6.17) и (6.18), отличный от нуля вклад в сумму (9.3) возможен только в трех случаях:
. Согласно формулам (6.15), (6.17) и (6.18), отличный от нуля вклад в сумму (9.3) возможен только в трех случаях:
1) в начальном и конечном детерминантах различны только две орбитали;
2) начальный и конечный детерминанты различаются только одной орбиталью;
3) все орбитали, входящие в начальный и конечный детерминанты, одинаковы. Из формул (6.15) — (6.18) видно также, что интересующие нас выражения содержат только по две орбитали; надо вычислить матричные элементы вида

В случае 1 две различные орбитали должны описывать электроны в незаполненных оболочках, поскольку для заполненных оболочек все состояния в детерминантах Слэтера одни и те же. В случае 2 различающиеся состояния также должны описывать электрон в незаполненной оболочке. Таким образом, вклад, описываемый
формулой (6.17), можно записать в виде

Здесь  состояния различны в начальном и конечном детерминантах (обозначенных соответственно индексами i и i). Покажем теперь, что сумма по заполненным оболочкам равна нулю. Действительно,
состояния различны в начальном и конечном детерминантах (обозначенных соответственно индексами i и i). Покажем теперь, что сумма по заполненным оболочкам равна нулю. Действительно,

где Ф — некоторая функция  , а
, а

Поскольку по предположению  или
или  имеют место оба эти неравенства), выражение (9.10) равно нулю. Однако результат (9.10) можно использовать и в случае, когда
имеют место оба эти неравенства), выражение (9.10) равно нулю. Однако результат (9.10) можно использовать и в случае, когда  Обменный интеграл можно вычислить тем же способом, что и в гл. 6 [см. (6.45)-(6.53)]:
Обменный интеграл можно вычислить тем же способом, что и в гл. 6 [см. (6.45)-(6.53)]:

где

Здесь приняты те же обозначения, что и в равенствах (6.48) и (6.49). После интегрирования по  остаются только члены, в которых
остаются только члены, в которых  Интегрируя затем по
Интегрируя затем по  находим окончательно
находим окончательно

Поскольку либо  либо
либо  (либо и то и другое), это выражение также обращается в нуль.
(либо и то и другое), это выражение также обращается в нуль.
В третьем случае, когда начальные и конечные состояния электронов идентичны, результат дается формулой (6.15). Для наших целей его можно переписать в виде

Здесь использован тот факт, что сумма равна нулю при  и симметрична относительно перестановки
и симметрична относительно перестановки  . Как можно усмотреть из соотношений (9.10) и (9.14), сумма по заполненным оболочкам
. Как можно усмотреть из соотношений (9.10) и (9.14), сумма по заполненным оболочкам  есть константа, не зависящая от
есть константа, не зависящая от  . Как и раньше в случае (9.7), этот член можно отбросить. Тогда равенство (9.15) принимает вид
. Как и раньше в случае (9.7), этот член можно отбросить. Тогда равенство (9.15) принимает вид

Сумма по  для заполненных оболочек опять отбрасывается, и единственно существенный вклад сводится к следующему:
для заполненных оболочек опять отбрасывается, и единственно существенный вклад сводится к следующему:

Итак, при вычислении членов вида (9.3) надо рассматривать только случай, когда обе орбитали описывают электроны в незаполненных оболочках.
Эквивалентность дырок и электронов
Докажем теперь следующую важную и полезную теорему: расстояния между расщепленными уровнями в оболочке, в которой недостает  электронов, и в оболочке, содержащей N электронов, одинаковы. Этот результат был получен Гейзенбергом [22].
электронов, и в оболочке, содержащей N электронов, одинаковы. Этот результат был получен Гейзенбергом [22].
Прежде всего отметим, что  -оболочка, содержащая k эквивалентных электронов, имеет те же мультиплеты, что и оболочка, содержащая
-оболочка, содержащая k эквивалентных электронов, имеет те же мультиплеты, что и оболочка, содержащая  электронов. Это следует из общей процедуры получения мультиплетов для эквивалентных электронов, описанной в конце гл. 8. Пусть мы рассматриваем оболочку, содержащую
электронов. Это следует из общей процедуры получения мультиплетов для эквивалентных электронов, описанной в конце гл. 8. Пусть мы рассматриваем оболочку, содержащую  электронов. Выпишем квантовые числа
электронов. Выпишем квантовые числа  для всех занятых состояний так, как это сделано в табл. 15. Равным образом, мы можем описать ситуацию, рассматривая незанятые состояния, и составить таблицу, подобную табл. 15, для k электронов. Единственное различие состоит в том, что величины ML и
для всех занятых состояний так, как это сделано в табл. 15. Равным образом, мы можем описать ситуацию, рассматривая незанятые состояния, и составить таблицу, подобную табл. 15, для k электронов. Единственное различие состоит в том, что величины ML и  для данного состояния равны соответственно суммам всех
для данного состояния равны соответственно суммам всех  и всех
и всех  для незанятых одноэлектронных состояний, взятым с обратным знаком. Это, однако, не меняет разрешенных значений L и S.
для незанятых одноэлектронных состояний, взятым с обратным знаком. Это, однако, не меняет разрешенных значений L и S.
Рассмотрим теперь расстояния между энергетическими уровнями. Диагональные элементы выражения
(9.15) для  электронов можно записать в виде
электронов можно записать в виде

Первые три члена здесь можно отбросить, так как они дают результат, не зависящий от магнитных квантовых чисел. Следовательно, вклад диагональных элементов в величину расстояния между расщепленными уровнями для  электронов в незаполненной оболочке такой же, как и вклад k электронов.
электронов в незаполненной оболочке такой же, как и вклад k электронов.
Обратимся теперь к недиагональным элементам. Если различается одна (две) орбитали, мы имеем переход электрона из состояния  (и из
(и из  ) Это эквивалентно переходу дырки из
) Это эквивалентно переходу дырки из  в и, (и из
в и, (и из  , в
, в  ) и дает тот же вклад независимо от того, ведется ли рассмотрение с точки зрения электрона или дырки. Тем самым теорема доказана. Можно видеть, что (с точностью до общего сдвига энергии, обусловленного полным числом электронов) структура уровней для k электронов и для
) и дает тот же вклад независимо от того, ведется ли рассмотрение с точки зрения электрона или дырки. Тем самым теорема доказана. Можно видеть, что (с точностью до общего сдвига энергии, обусловленного полным числом электронов) структура уровней для k электронов и для  электронов количественно одна и та же.
электронов количественно одна и та же.
Интегралы по углам
Угловая и спиновая часть общего интеграла имеет 
 (9.19)
(9.19)
Разлагая  по сферическим гармоникам и рассматривая интеграл по телесному углу
по сферическим гармоникам и рассматривая интеграл по телесному углу  мы получаем
мы получаем

(Это равенство определяет коэффициенты  ) Интегрирование по
) Интегрирование по  дает
дает

(индексы переставлены). Поэтому полный матричный элемент (с учетом радиальной части) равен

где

Коэффициенты  определенные равенствами (9.20) и (6.49), были впервые вычислены Гонтом. Однако более удобной и симметричной оказывается формула Рака
определенные равенствами (9.20) и (6.49), были впервые вычислены Гонтом. Однако более удобной и симметричной оказывается формула Рака
 (9.24)
(9.24)
где функция V определена равенством (8.24).
Как было выше установлено [см. (6.50)], число  должно быть четным, причем
должно быть четным, причем

Интересны следующие частные случаи:

Введем обозначения:

где величина дается равенством (9.23). Очевидно, выражение  совпадает с первоначальным определением (9.13), a
совпадает с первоначальным определением (9.13), a  в (9.11) есть частный случай (9.28).
в (9.11) есть частный случай (9.28).
Правило сумм Слэтера
При вычислении энергетических уровней весьма удобным оказывается правило сумм Слэтера [23]. Это правило состоит в хорошо известном из математики утверждении, что след матрицы инвариантен относительно преобразований подобия. В пренебрежении спином это дает

Суммирование в левой части производится здесь по всем возможным наборам орбитальных квантовых чисел, удовлетворяющих соотношению  . Левая часть равенства (9.29) представляет собой след гамильтоновской матрицы в
. Левая часть равенства (9.29) представляет собой след гамильтоновской матрицы в  -непредставлении, точнее субматрицы, соответствующей данному значению М.
-непредставлении, точнее субматрицы, соответствующей данному значению М.
Правая часть есть сумма собственных значений энергии для тех L, которые совместимы с данным М. Преобразование от  -представления к
-представления к  -представлению унитарно, следовательно, соотношение (9.29) должно быть справедливо. С учетом спина это равенство принимает вид
-представлению унитарно, следовательно, соотношение (9.29) должно быть справедливо. С учетом спина это равенство принимает вид

При этом наборы магнитных чисел  в левой части, обозначенные индексом
в левой части, обозначенные индексом  должны удовлетворять соотношениям
должны удовлетворять соотношениям

Приведем пример применения правила сумм. Рассмотрим систему двух неэквивалентных электронов с орбитальными моментами k и  и спиновыми магнитными числами
и спиновыми магнитными числами  Возможные соотношения перечислены в следующей таблице:
Возможные соотношения перечислены в следующей таблице:

Вычислим матричный элемент  для случая
для случая  :
:

Найдем теперь сумму матричных элементов для двух функций, соответствующих значению  :
:

Из правила сумм мы знаем, что это выражение равно

Но  так как Е не может зависеть от М; действительно,
так как Е не может зависеть от М; действительно,  Поэтому, вычитая результат (9.31) из выражения (9.33), мы получаем величину
Поэтому, вычитая результат (9.31) из выражения (9.33), мы получаем величину  Эту процедуру можно продолжить, вычислив и остальные уровни.
Эту процедуру можно продолжить, вычислив и остальные уровни.
Мы вычислим энергии триплегных состояний, полагая  Чтобы получить энергии синглетов, возьмем
Чтобы получить энергии синглетов, возьмем  или
или  Для функций с различными значениями
Для функций с различными значениями  обменный член исчезает. Поэтому значение
обменный член исчезает. Поэтому значение  соответствующее данному
соответствующее данному  , оказывается равным нулю в двух случаях:
, оказывается равным нулю в двух случаях:  Зная энергию триплетного состояния, мы можем определить и энергию синглетного состояния с помощью правила сумм. Поскольку обменный член входит в энергию триплетного состояния (9.31) с отрицательным знаком и отсутствует в матричных элементах, диагональных по
Зная энергию триплетного состояния, мы можем определить и энергию синглетного состояния с помощью правила сумм. Поскольку обменный член входит в энергию триплетного состояния (9.31) с отрицательным знаком и отсутствует в матричных элементах, диагональных по  он войдет с положительным знаком в энергию синглетного состояния. Это согласуется с результатом для пара-гелия.
он войдет с положительным знаком в энергию синглетного состояния. Это согласуется с результатом для пара-гелия.
Нужно отметить, что правило сумм не всегда достаточно для вычисления уровней энергии. Например, в случае трех неэквивалентных  -электронов мы имеем состояния
-электронов мы имеем состояния  и 25. При
и 25. При  , что получается, когда
, что получается, когда  энергию
энергию  -терма найти легко. Однако существуют три возможности, при которых реализуется значение
-терма найти легко. Однако существуют три возможности, при которых реализуется значение  . Поэтому правило сумм даст только сумму энергий двух
. Поэтому правило сумм даст только сумму энергий двух  -мультиплетов.
-мультиплетов.
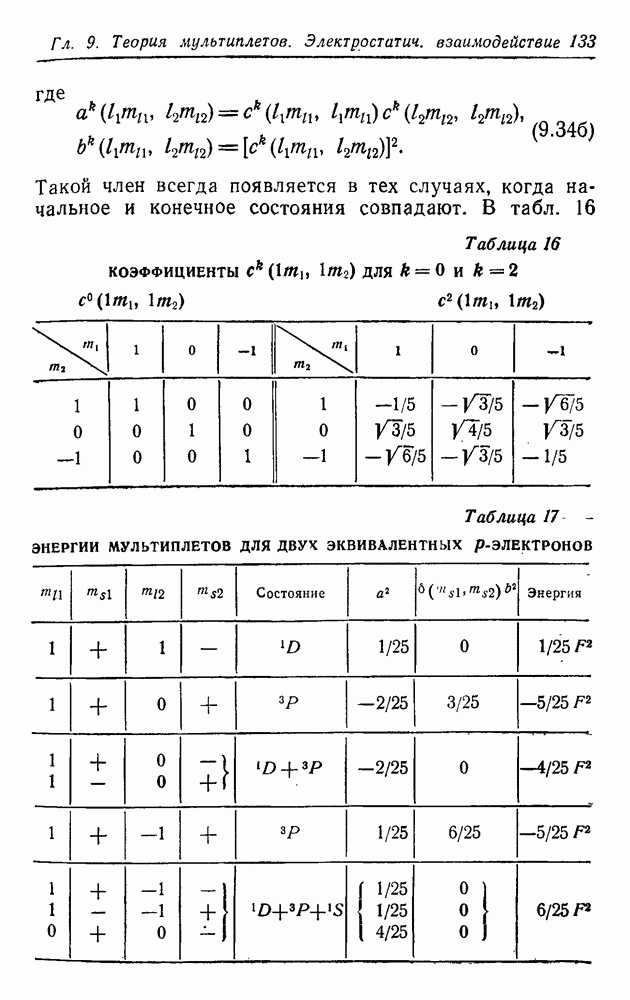
Рассмотрим теперь случай двух эквивалентных р-электронов  . Мы имеем
. Мы имеем

где

Такой член всегда появляется в тех случаях, когда начальное и конечное состояния совпадают. В табл. 16
Таблица 16
коэффициенты  для
для 

Таблица 17. ЭНЕРГИИ МУЛЬТИПЛЕТОВ ДЛЯ ДВУХ ЭКВИВАЛЕНТНЫХ Р-ЭЛЕКТРОНОВ

приведены значения  для
для  . Из условий (6.50) явствует, что только эти два значения k дают отличный от нуля вклад при
. Из условий (6.50) явствует, что только эти два значения k дают отличный от нуля вклад при  .
.
В табл. 17 перечислены возможные мультиплеты и их энергии. Поскольку при  всегда получается один и тот же член,
всегда получается один и тот же член,  мы опустим его. Из табл. 17 видно, что с помощью правила сумм можно не только определить все уровни энергии, но и вычислить энергию
мы опустим его. Из табл. 17 видно, что с помощью правила сумм можно не только определить все уровни энергии, но и вычислить энергию  -состояния тремя независимыми способами, и все они согласуются друг с другом. Это происходит и во многих других случаях. Без вычисления радиальных интегралов (которые, конечно, должны быть положительны) табл. 17 и ей подобные дают расположение различных энергетических уровней, возникающих из данной конфигурации, и отношение энергетических расстояний между ними. Результаты для нескольких конфигураций приведены в табл. 18.
-состояния тремя независимыми способами, и все они согласуются друг с другом. Это происходит и во многих других случаях. Без вычисления радиальных интегралов (которые, конечно, должны быть положительны) табл. 17 и ей подобные дают расположение различных энергетических уровней, возникающих из данной конфигурации, и отношение энергетических расстояний между ними. Результаты для нескольких конфигураций приведены в табл. 18.
Таблица 18. СТРУКТУРА МУЛЬТИПЛЕТОВ ДЛЯ РАЗЛИЧНЫХ ЭЛЕКТРОННЫХ КОНФИГУРАЦИЙ

Средняя энергия
Во всем, что делалось выше, вклад в энергию мультиплета, не зависящий от  , т. е. вклад, одинаковый для всех мультиплетов данной конфигурации, отбрасывался. Теперь мы вычислим его, Как мы знаем,
, т. е. вклад, одинаковый для всех мультиплетов данной конфигурации, отбрасывался. Теперь мы вычислим его, Как мы знаем,
полная энергия дается выражением

где f — одноэлектронный оператор, a g — оператор взаимодействия между электронами, равный  . Среднее значение одноэлектронного оператора легко выразить через радиальные волновые функции
. Среднее значение одноэлектронного оператора легко выразить через радиальные волновые функции

Здесь  — число электронов в
— число электронов в  -оболочке, как заполненной, так и незаполненной. Член, описывающий кинетическую энергию в (9.36), можно упростить (см. [3.])
-оболочке, как заполненной, так и незаполненной. Член, описывающий кинетическую энергию в (9.36), можно упростить (см. [3.]) 
Взаимодействие одного электрона с заполненной оболочкой рассматривалось в начале этой главы. Полагая  мы получаем из формулы (9.10)
мы получаем из формулы (9.10)

Далее, равенство (9.14) дает

где величины  определены формулами (9.11) и (9.13). Тем самым мы вычислили всю энергию взаимодействия между электронами внутри заполненных оболочек, а также между электронами в незаполненных и заполненных оболочках.
определены формулами (9.11) и (9.13). Тем самым мы вычислили всю энергию взаимодействия между электронами внутри заполненных оболочек, а также между электронами в незаполненных и заполненных оболочках.
Мы можем также формально применить равенства (9.37) и (9.38) для вычисления энергии взаимодействия
одного электрона в незаполненной оболочке со всеми другими электронами той же оболочки. Посмотрим сначала, какова была бы эта энергия, если бы оболочка была заполнена. Мы имеем

Равенство во второй строчке (9.39) следует из того, что по определению  когда
когда  Последняя строчка в (9.39) получается, если учесть, что, согласно (9.26),
Последняя строчка в (9.39) получается, если учесть, что, согласно (9.26),  . Член с
. Член с  не дает вклада в сумму, стоящую в левой части (9.39). Соответственно это равенство можно рассматривать как среднюю энергию взаимодействия
не дает вклада в сумму, стоящую в левой части (9.39). Соответственно это равенство можно рассматривать как среднюю энергию взаимодействия  электрона со всеми остальными
электрона со всеми остальными  электронами той же оболочки. Конечно, это выражение не зависит от
электронами той же оболочки. Конечно, это выражение не зависит от  Поэтому мы можем определить среднюю энергию
Поэтому мы можем определить среднюю энергию  взаимодействия одного электрона в данной оболочке с любым другим электроном как выражение (9.39), поделенное на
взаимодействия одного электрона в данной оболочке с любым другим электроном как выражение (9.39), поделенное на  Опуская индекс
Опуская индекс  , находим
, находим

Сумма, конечно, содержит только четные значения 
Будем считать теперь, что в незаполненной оболочке  находятся N электронов, и рассмотрим все возможные распределения этих электронов по
находятся N электронов, и рассмотрим все возможные распределения этих электронов по  -состояниям, совместимым с принципом Паули. При усреднении по всем таким распределениям учтем, что вероятность заполнения любого
-состояниям, совместимым с принципом Паули. При усреднении по всем таким распределениям учтем, что вероятность заполнения любого  -состояния одна и та же.
-состояния одна и та же.
Тогда энергия взаимодействия каждого действительно присутствующего электрона с любым другим электроном будет в среднем равна величине (9.40). Энергия взаимодействия N электронов, усредненная по всем распределениям, составит поэтому

 — число взаимодействующих электронных пар]. Таким образом, мы знаем сумму всех диагональных элементов энергии взаимодействия,
— число взаимодействующих электронных пар]. Таким образом, мы знаем сумму всех диагональных элементов энергии взаимодействия,  в
в  -представлении. Эта сумма равна средней энергии взаимодействия (9.41), помноженной на число возможных состояний в
-представлении. Эта сумма равна средней энергии взаимодействия (9.41), помноженной на число возможных состояний в  -представленин. Последнее в свою очередь равно числу возможных распределений N электронов по
-представленин. Последнее в свою очередь равно числу возможных распределений N электронов по  состояниям, т. е.
состояниям, т. е.  . Используем теперь правило сумм. Сумма диагональных элементов энергии взаимодействия в
. Используем теперь правило сумм. Сумма диагональных элементов энергии взаимодействия в  -представлении равна сумме собственных значений энергии в
-представлении равна сумме собственных значений энергии в  -представлении. Поэтому взвешенное среднее этих собственных значений должно равняться величине (9.41):
-представлении. Поэтому взвешенное среднее этих собственных значений должно равняться величине (9.41):

Здесь, разумеется,

и E(L, S) означает электростатическую энергию терма LS, которую мы уже вычислили в этой главе. Используя результаты табл. 17 или 18, легко можно убедиться в справедливости равенств (9.42) и (9.40).
Более того, мы можем теперь обобщить теорему Купмена (см. гл. 6) на случай незаполненных оболочек. Используя равенства  и уравнения Хартри — Фока, усредненные по углам [см. (6.27)], легко показать, что собственное значение энергии Хартри — Фока равно разности между средними энергиями атома и иона. При этом средние определены в смысле (9.42) и сделано приближение Купмена, т. е. собственные функции атома считаются такими же, как и собственные функции иона.
и уравнения Хартри — Фока, усредненные по углам [см. (6.27)], легко показать, что собственное значение энергии Хартри — Фока равно разности между средними энергиями атома и иона. При этом средние определены в смысле (9.42) и сделано приближение Купмена, т. е. собственные функции атома считаются такими же, как и собственные функции иона.
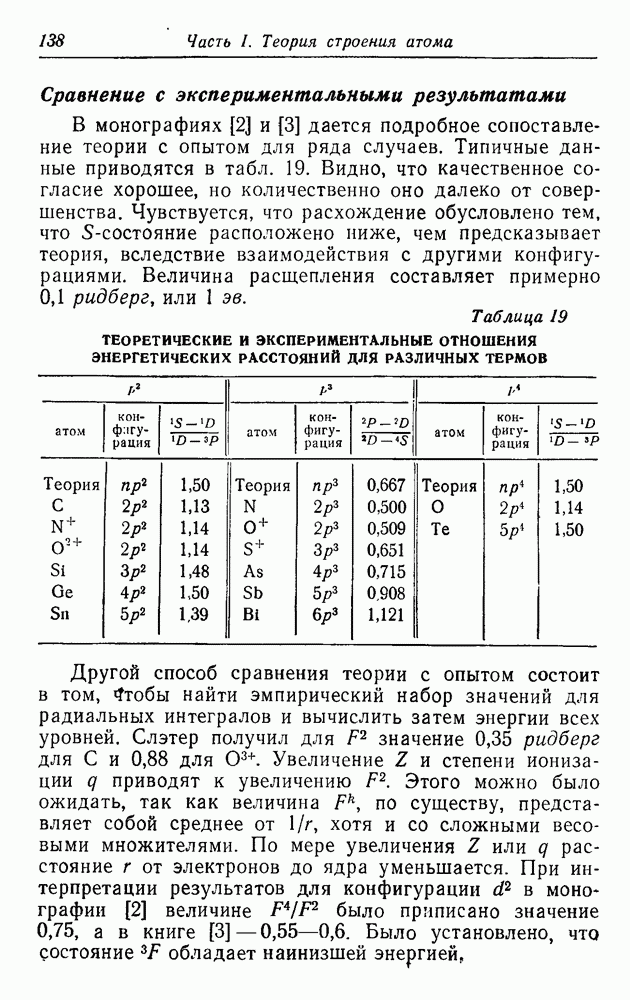
Сравнение с экспериментальными результатами
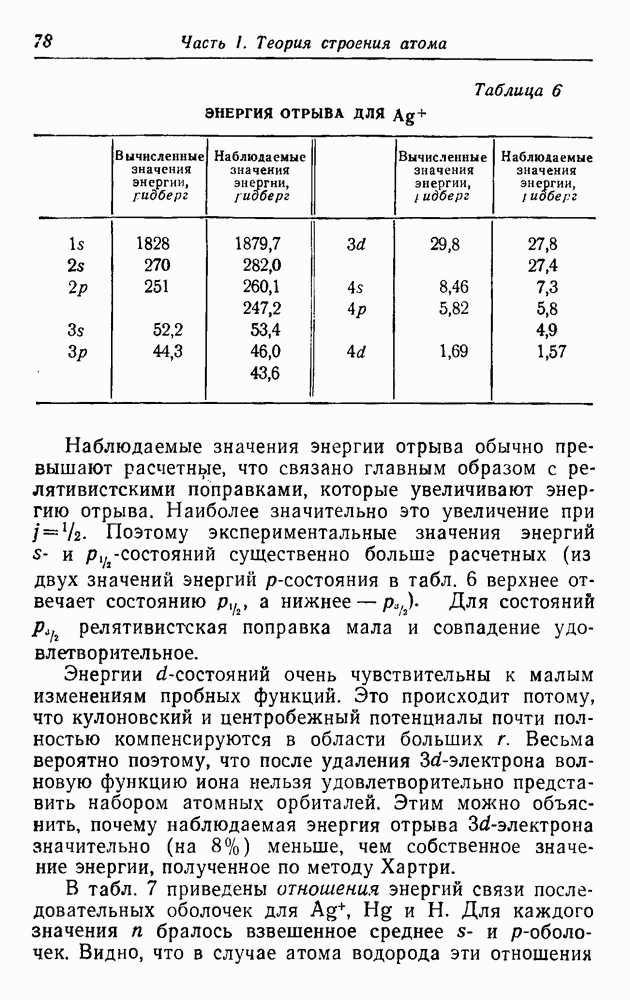
В монографиях [2] и [3] дается подробное сопоставление теории с опытом для ряда случаев. Типичные данные приводятся в табл. 19. Видно, что качественное согласие хорошее, но количественно оно далеко от совершенства. Чувствуется, что расхождение обусловлено тем, что  -состояние расположено ниже, чем предсказывает теория, вследствие взаимодействия с другими конфигурациями. Величина расщепления составляет примерно 0,1 ридберг, или
-состояние расположено ниже, чем предсказывает теория, вследствие взаимодействия с другими конфигурациями. Величина расщепления составляет примерно 0,1 ридберг, или 
Таблица 19. ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ОТНОШЕНИЯ ЭНЕРГЕТИЧЕСКИХ РАССТОЯНИЙ ДЛЯ РАЗЛИЧНЫХ ТЕРМОВ

Другой способ сравнения теории с опытом состоит в том, чтобы найти эмпирический набор значений для радиальных интегралов и вычислить затем энергии всех уровней. Слэтер получил для  значение 0,35 ридберг для С и 0,88 для
значение 0,35 ридберг для С и 0,88 для  . Увеличение Z и степени ионизации q приводят к увеличению
. Увеличение Z и степени ионизации q приводят к увеличению  . Этого можно было ожидать, так как величина
. Этого можно было ожидать, так как величина  по существу, представляет собой среднее от
по существу, представляет собой среднее от  хотя и со сложными весовыми множителями. По мере увеличения Z или q расстояние
хотя и со сложными весовыми множителями. По мере увеличения Z или q расстояние  от электронов до ядра уменьшается. При интерпретации результатов для конфигурации
от электронов до ядра уменьшается. При интерпретации результатов для конфигурации  в монографии [2] величине
в монографии [2] величине  было приписано значение 0,75, а в книге
было приписано значение 0,75, а в книге  Было установлено, что состояние
Было установлено, что состояние  обладает наинизшей энергией,
обладает наинизшей энергией,
В результате многочисленных вычислений было выведено несколько правил:
1. Низшая энергия соответствует максимальному спину. Поскольку максимальный спин соответствует симметричной комбинации индивидуальных спиновых функций, пространственная функция будет антисимметричной; ей соответствует наибольшее кулоновское отталкивание (см. стр. 38).
2. Среди мультиплетов с максимальным спином низшая энергия соответствует наибольшему значению L. Большим значениям ML соответствуют орбиты, близкие к экваториальной плоскости. Это позволяет электронам находиться в среднем далеко друг от друга, уменьшая тем самым их энергию взаимодействия.
Эти два правила известны под названием правила Хунда. Они были проверены и подтверждены исследованием многих спектров, включая спектры редкоземельных элементов, содержащих  -электроны. Эти правила применимы только к низшему энергетическому состоянию.
-электроны. Эти правила применимы только к низшему энергетическому состоянию.
Отнюдь не верно, что все состояния с максимальным спином S обладают меньшей энергией, чем все состояния с ближайшим меньшим значением S. В конфигурации  состояние обычно расположено ниже, чем
состояние обычно расположено ниже, чем  в конфигурации
в конфигурации  состояние
состояние  всегда ниже, чем наивысшее из двух
всегда ниже, чем наивысшее из двух  -состояний, а также ниже, чем
-состояний, а также ниже, чем  -состояние. Подобным же образом для значения S, меньшего, чем максимальное, состояние с наибольшим L не всегда является наинизшим. Так, в простом случае
-состояние. Подобным же образом для значения S, меньшего, чем максимальное, состояние с наибольшим L не всегда является наинизшим. Так, в простом случае  иаинизшее синглетное состояние есть
иаинизшее синглетное состояние есть  а не
а не  (Для оболочечной структуры ядра правило Хунда приводит к обратной картине, так как там действуют силы притяжения.)
(Для оболочечной структуры ядра правило Хунда приводит к обратной картине, так как там действуют силы притяжения.)
Применяя это правило, мы можем найти низшее состояние для конфигурации  . В табл. 20 указаны низший мультиплет для конфигурации
. В табл. 20 указаны низший мультиплет для конфигурации  энергия взаимодействия между электронами в
энергия взаимодействия между электронами в  -оболочке для этого мультиплета и разность энергий для
-оболочке для этого мультиплета и разность энергий для  электронов.
электронов.
Помимо общего увеличения энергии взаимодействия (члены с  ), обусловленного добавлением электронов,
), обусловленного добавлением электронов,
Таблица 20. ЭНЕРГИИ МУЛЬТИПЛЕТОВ ДЛЯ КОНФИГУРАЦИИ 

имеет место еще увеличение энергии связи (больший отрицательный вклад от  ) при переходе от первого электрона ко второму и от второго к третьему. Затем имеется обрыв и повторение той же картины. Мы показали, таким образом, что наполовину заполненной
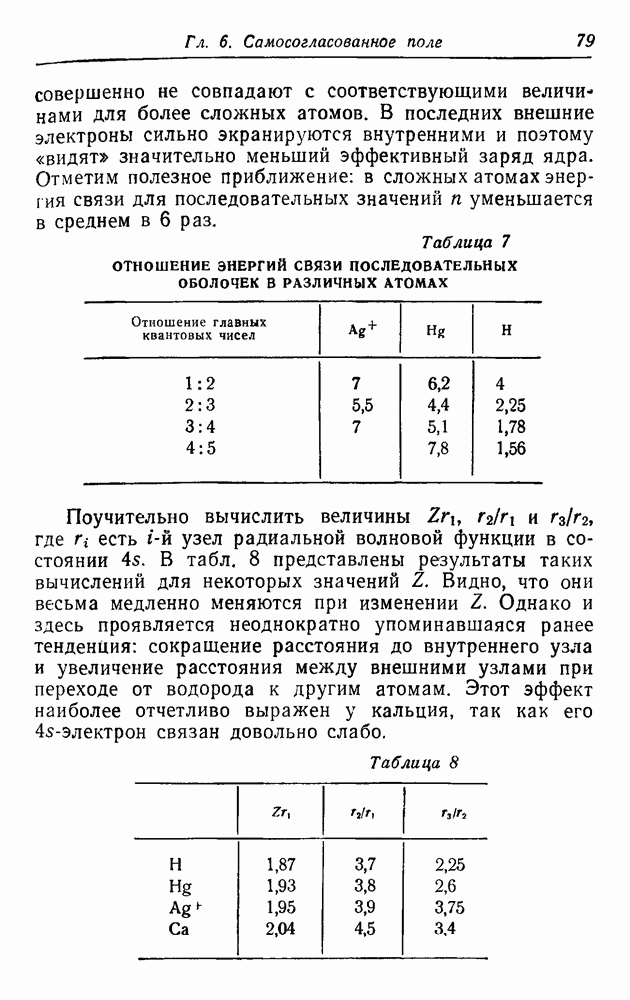
) при переходе от первого электрона ко второму и от второго к третьему. Затем имеется обрыв и повторение той же картины. Мы показали, таким образом, что наполовину заполненной  -оболочке (3 электрона) соответствует особенно высокий потенциал ионизации. То же самое можно показать и для заполненных наполовину d- и
-оболочке (3 электрона) соответствует особенно высокий потенциал ионизации. То же самое можно показать и для заполненных наполовину d- и  -оболочек. Такое поведение наблюдалось для потенциала ионизации различных атомов (см. стр. 82).
-оболочек. Такое поведение наблюдалось для потенциала ионизации различных атомов (см. стр. 82).
Конфигурационное взаимодействие
Пренебрегая в гамильтониане всеми спиновыми эффектами, мы нашли, что операторы L и S коммутируют с гамильтонианом. Мы видели, что значения L и S можно квантовать независимо. Это называется связью Рассел—Саундерса, или  -связью. Строго говоря, только величины L, S, ML и Ms являются хорошими квантовыми
-связью. Строго говоря, только величины L, S, ML и Ms являются хорошими квантовыми
числами. Четность состояния определяется суммой индивидуальных значений  . Поэтому, хотя последние сами по себе и не являются хорошими квантовыми числами, четность или нечетность их сумм остается хорошим квантовым числом. Однако, поскольку разность между энергетическими уровнями, возникающими для различных конфигураций, вообще говоря, велика по сравнению с электростатической энергией взаимодействия, мы предположили, что уравнения Хартри — Фока дают в нулевом приближении волновые функции, пригодные для вычисления энергий взаимодействия. При более строгом подходе нужно было бы допустить возможность смешения конфигураций. Действительно, несколько конфигураций могут приводить к мультиплету с одними и теми же значениями
. Поэтому, хотя последние сами по себе и не являются хорошими квантовыми числами, четность или нечетность их сумм остается хорошим квантовым числом. Однако, поскольку разность между энергетическими уровнями, возникающими для различных конфигураций, вообще говоря, велика по сравнению с электростатической энергией взаимодействия, мы предположили, что уравнения Хартри — Фока дают в нулевом приближении волновые функции, пригодные для вычисления энергий взаимодействия. При более строгом подходе нужно было бы допустить возможность смешения конфигураций. Действительно, несколько конфигураций могут приводить к мультиплету с одними и теми же значениями  . Учет этого обстоятельства составляет второе приближение, если нулевое приближение хартри — фоковское, а первое состоит в учете электростатического взаимодействия.
. Учет этого обстоятельства составляет второе приближение, если нулевое приближение хартри — фоковское, а первое состоит в учете электростатического взаимодействия.
Мы приходим, таким образом, к построению субматрицы гамильтониана, связывающей различные конфигурации при данном значении  . Пусть строки и столбцы соответствуют различным конфигурациям. Выше мы рассматривали только диагональные элементы этой матрицы, т. е. элементы между одной и той же конфигурацией. Рассмотрим теперь всю матрицу.
. Пусть строки и столбцы соответствуют различным конфигурациям. Выше мы рассматривали только диагональные элементы этой матрицы, т. е. элементы между одной и той же конфигурацией. Рассмотрим теперь всю матрицу.
Если вклад дают только две конфигурации, то интересующая нас матрица имеет вид

Собственные значения энергии суть

Величина квадратного корня больше, чем  Следовательно, элемент
Следовательно, элемент  выражающий степень смешения, будет «раздвигать» собственные значения дальше друг от друга. Синглетное
выражающий степень смешения, будет «раздвигать» собственные значения дальше друг от друга. Синглетное  -состояние, например, понижается за счет его взаимодействия с более высокими синглетнымм
-состояние, например, понижается за счет его взаимодействия с более высокими синглетнымм  -состояниями.
-состояниями.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Часть I. ТЕОРИЯ СТРОЕНИЯ АТОМА
- 1. УРАВНЕНИЕ ШРЕДИНГЕРА И ПРИБЛИЖЕННЫЕ МЕТОДЫ ЕГО РЕШЕНИЯ
- 2. ИНТЕГРАЛЫ ДВИЖЕНИЯ
- 3. ТОЖДЕСТВЕННОСТЬ ЧАСТИЦ И СИММЕТРИЯ
- 4. ДВУХЭЛЕКТРОННЫЕ АТОМЫ. РАСЧЕТ ПО ТЕОРИИ ВОЗМУЩЕНИЙ
- 5. ДВУХЭЛЕКТРОННЫЕ АТОМЫ. РАСЧЕТ ВАРИАЦИОННЫМ МЕТОДОМ
- 6. САМОСОГЛАСОВАННОЕ ПОЛЕ
- 7. СТАТИСТИЧЕСКАЯ МОДЕЛЬ ТОМАСА—ФЕРМИ
- 8. ТЕОРИЯ МУЛЬТИПЛЕТОВ. СЛОЖЕНИЕ МОМЕНТОВ
- 9. ТЕОРИЯ МУЛЬТИПЛЕТОВ. ЭЛЕКТРОСТАТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ
- 10. ТЕОРИЯ МУЛЬТИПЛЕТОВ. МАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ
- 11. МОЛЕКУЛЫ
- 12. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ ИЗЛУЧЕНИЯ
- 13. ИНТЕНСИВНОСТЬ ИЗЛУЧЕНИЯ
- 14. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
- 15. СТОЛКНОВЕНИЯ АТОМОВ С ЗАРЯЖЕННЫМИ ЧАСТИЦАМИ
- Часть II. РЕЛЯТИВИСТСКИЕ ТЕОРИИ
- 16. УРАВНЕНИЕ КЛЕЙНА—ГОРДОНА
- 17. УРАВНЕНИЕ ДИРАКА. ФОРМАЛЬНАЯ ТЕОРИЯ
- 18. РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА
- Часть III. ВВЕДЕНИЕ В ТЕОРИЮ ПОЛЯ
- 19. КВАНТОВАНИЕ ПОЛЯ
- 20. ВТОРИЧНОЕ КВАНТОВАНИЕ НЕСКОЛЬКИХ ПОЛЕЙ ЧАСТИЦ
- 21. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ. КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- ЛИТЕРАТУРА