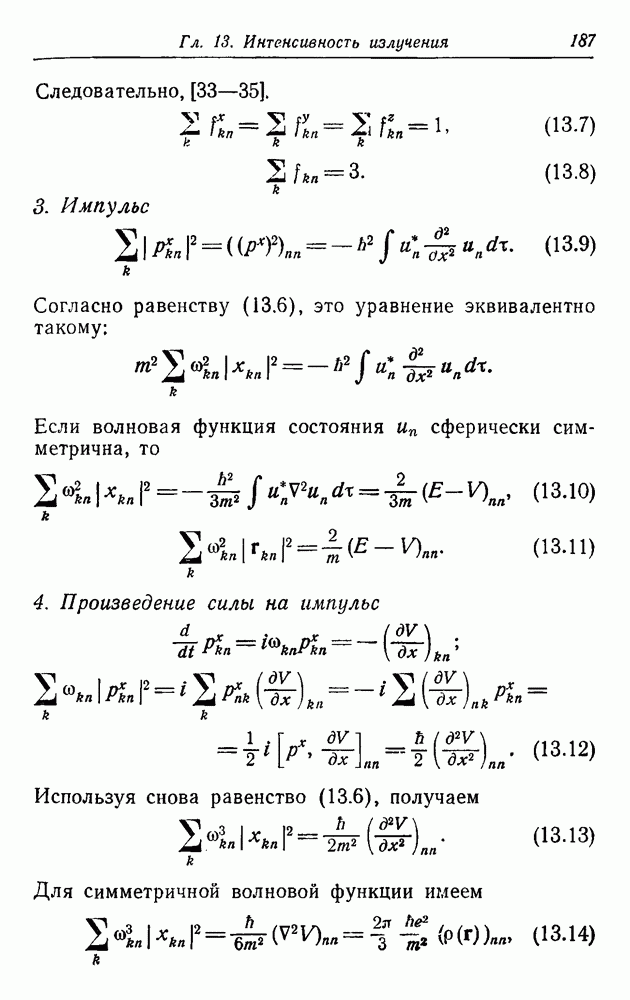13. ИНТЕНСИВНОСТЬ ИЗЛУЧЕНИЯ

Правила сумм

Нижеследующие правила сумм полезны при оценке интенсивности излучения. Все суммирования проводятся по полному набору собственных значений энергии, т. е. ведется суммирование по дискретному спектру и интегрирование по непрерывному спектру.

1. Дипольный момент

Если волновая функция состояния изотропна, то

Если определить величину как , то

2 Сила осциллятора

Сила осциллятора определяется равенствами

Напомним, что

Следовательно, [33—35].

3. Импульс

Согласно равенству (13.6), это уравнение эквивалентно такому:

Если волновая функция состояния сферически симметрична, то

    (13.11)

4. Произведение силы на импульс

Используя снова равенство (13.6), получаем

    (13.13)

Для симметричной волновой функции имеем

где — плотность положительного заряда, ответственного за потенциальную энергию V. Для неэкранированного ядра , так что

    (13.15)

Далее,

5. Квадрат силы

В случае когда волновая функция состояния сфери чески симметрична, получаем

    (13.18)

И

Сводка результатов

Сводка результатов для сумм вида приведена в табл. 22. В ней предполагается (для всех , кроме случая р=1), что волновая функция состояния сферически симметрична. Величины типа можно получить, умножая указанные в табл. 22 значения сумм на 3. Ясно, что в этом последнем случае результат будет справедлив независимо от предположения о сферической симметрии.

Таблица 22. ПРАВИЛА СУММ

Система многих электронов

Приведенные выше правила сумм получены для случая переходов одного электрона. Для системы Z электронов соответствующий интеграл принимает вид

В дипольном приближении он равен

В этом случае находим

    (13.22)

Атом водорода

В качестве примера приложения правил сумм приведем результаты для водорода, считая, что электрон находится в низшем состоянии с главным квантовым числом, равным 1 (и сферически симметричной волновой функцией)

Сумма

Здесь символ представляет собой частоту Ридберга. Как можно заключить из этой таблицы, средняя частота переходов из основного состояния равна просто среднеквадратичная частота есть и кубический корень из среднего куба частоты перехода равен

В случае имеем . Так как , то для получаем . Если Для случая этот интеграл расходится, а при он конечен. Отсюда следует, что при величина ведет себя как , где с — константа — число. Мы знаем, что интеграл сходится, а интеграл расходится. Отсюда .

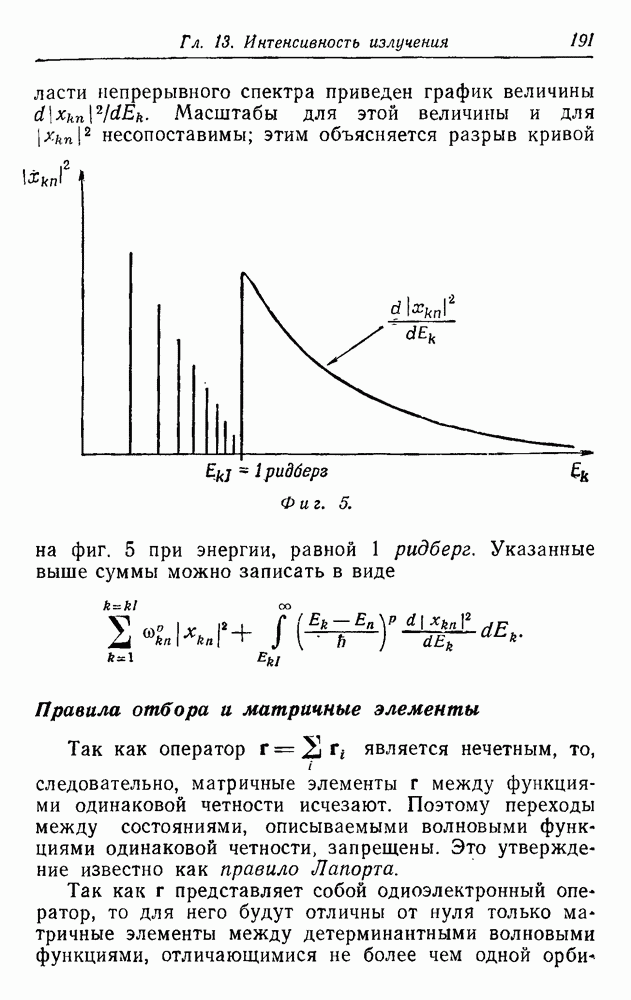
На фиг. 5 показан общий ход изменения величины в зависимости от энергии при фиксированном для атома водорода. Энергия ионизации ридберг при Наиболее удобным для нас было нормировать волновые функции непрерывного спектра на -функцию от энергии. Это отмечено на фиг. 5 — в области

непрерывного спектра приведен график величины Масштабы для этой величины и для несопоставимы; этим объясняется разрыв кривой на фиг. 5 при энергии, равной 1 ридберг.

Фиг. 5.

Указанные выше суммы можно записать в виде

Правила отбора и матричные элементы

Так как оператор является нечетным, то, следовательно, матричные элементы между функциями одинаковой четности исчезают. Поэтому переходы между состояниями, описываемыми волновыми функциями одинаковой четности, запрещены. Это утверждение известно как правило Лапорта.

Так как представляет собой одиоэлектронный оператор, то для него будут отличны от нуля только матричные элементы между детерминантными волновыми функциями, отличающимися не более чем одной орбиталью.

Учитывая правило Лапорта, мы приходим к заключению, что у имеются только матричные элементы между детерминантными волновыми функциями, обязательно отличающимися одной орбиталью. Согласно формуле (6.13), подобный матричный элемент сводится к , где орбитали , i различны. Итак, надо вычислить следующие величины:

    (13-24)

где различными переменными могут быть

и

При этом правую часть равенства (13.24) можно записать в виде

    (13.25)

где , и в случае весь матричный элемент нужно еще помножить на Интегрируя сначала по угловым переменным, мы получаем, согласно формулам (6.49) и (6.50),

Допустим, что Из (13.26) вытекает, что -нечетное, следовательно, этому возможны только такие переходы:

и в любом случае выполняются следующие правила отбора:

    (13.27)

Правила отбора для магнитного квантового числа (существенные в теории эффекта Зеемана) связаны (в классическом пределе) с моментом количества движения, уносимым излучением. Излученный свет, распространяющийся вдоль оси и поляризованный по кругу, уносит единицу (со знаком «плюс» или «минус») момента количества движения относительно оси z [29]. Отсюда . Классическую аналогию нелегко найти для случая когда излучается свет, поляризованный линейно в направлении оси z и, следовательно, распространяющийся в плоскости Чтобы определить его момент количества движения, нужно было бы рассмотреть момент количества движения электрона относительно направления распространения света, а это сделать нелегко, так как в качестве квантовой величины выбрана компонента не коммутирующая с Однако, согласно квантовой механике, полный орбитальный момент количества движения изменяется на ±1, чем и обеспечивается возможность единичного значения момента количества движения испущенного света.

Когда мы имеем дело с одноэлектронными спектрами, такими, как у водорода и атомов щелочных металлов, правила отбора (13.27) полностью определяют спектр. В случае многоэлектронного атома, если состояния описываются одной конфигурацией, возможны лишь такие изменения конфигурации, при которых меняются квантовые числа только одного электрона, причем изменение I равно ±1. Действительно, представляет собой одноэлектронный оператор. Это так называемые одноэлектронные скачки. Наблюдаются переходы, в которых происходит изменение двух пар чисел (двухэлектронные скачки). Это интерпретируется как свидетельство неточности описания энергетических уровней с помощью только одной конфигурации.

Интегралы по угловым переменным в выражении (13.25) можно вычислить. Это дает (мы опустили индекс , и заменили на ):

    (13.28)

Во всех случаях, когда встречаются знаки нужно брать одновременно или верхние, или нижние.

Из формул (13.28) вытекают равенства

    (13.29)

Здесь просуммированы интенсивности переходов с любой поляризацией из состояния с заданными квантовыми числами в состояния со всеми при фиксированных Отсюда следует вывод, что время жизни состояния зависит только от . Далее,

    (13.39)

Формулы (13.30) дают суммарную интенсивность всех зеемановских компонент спектральной линии, имеющих одинаковую поляризацию. Видно, что эта полная интенсивность одинакова для каждой из трех компонент лоренцовского триплета при нормальном эффекте Зеемана. Формулы (13.29), так же и (13.30), являются следствиями изотропности пространства.

Теперь можно доказать следующие два «правила сумм для парциальных сил осциллятора» (см. [7]):

Две эти суммы при сложении дают единицу, как и следовало ожидать согласно правилу сумм (13.7). Так как первая сумма положительна, можно сделать вывод, что среди переходов поглощение преобладает. Из того, что вторая сумма отрицательна, можно заключить, что при переходах преобладает испускание . Поскольку с увеличением главного квантового числа энергия растет, формулы (13.31) показывают, что изменение главного и орбитального квантовых чисел в одну и ту же сторону более вероятно, чем прыжок в противоположных направлениях. Подобным же образом последние два равенства (13.28) показывают, что абсолютное значение вероятнее всего, изменяется в том же направлении, что и I. Оба результата имеют классические аналоги, которые можно получить, исследуя эллиптическое движение электрона.

Правила отбора для многоэлектронных систем

Возвращаясь к выводу правил отбора для сложного атома, рассмотрим сначала случай, когда имеет место Поскольку оператор коммутирует с S, он

не может связывать состояния с различными квантовыми числами S или Поэтому переходы между уровнями различной мультиплетности запрещены, так что Для одноэлектронных спектров также выполняется правило

Так как оператор представляет собой вектор типа вектора А по отношению к операторам L и J, т. е. он подобен рассмотренному в (10.17), то мы получаем правила отбора: . Как и в случае магнитного квантового числа, матричные элементы оператора z не исчезают лишь при . Для оператора отличны от нуля только матричные элементы с Поляризация света определяется такими же правилами, как и для одноэлектронных спектров.

Для любого атома строго запрещен переход из состояния с в состояние с . Действительно, рассмотрим интеграл

Поскольку волновые функции не изменятся при любом повороте системы координат. Если, в частности, выбрать в качестве оси вращения направление вектора к, то не будет также меняться и екгл Можно, например, для каждого повернуть систему на 180° вокруг к. Тогда и интеграл изменит знак, оставаясь неизменным по величине, что возможно только при равенстве его нулю.

Подытожим прачила отбора для -связи:

1. Четность меняется.

2. Изменение конфигурации должно подчиняться условию

3. Мультиплетность не меняется;

8. Переход строго запрещен.

Как видно, эти правила совершенно аналогичны рассмотренным ранее в связи с одноэлектронными спектрами. Правила 1, 7, 8 и 9 справедливы при произвольной связи. Правило 2 сохраняет силу до тех пор, пока можно пользоваться конфигурационным описанием. Остальные правила верны только для случая -связи. Напомним, что всякий раз, когда для описания состояния системы используются одноэлектронные волновые функции, четность состояния есть если равна четному (или нечетному) числу. Даже если состояние системы не может быть аппроксимировано совокупностью одноэлектронных функций, мы все же можем с определенностью говорить о четности состояния благодаря тому, что добавки, появившиеся в качестве примесей к одноэлектронным собственным функциям, должны обладать той же самой четностью. Иными словами, в том, что касается четности, одноэлектронные волновые функции всегда дают хорошее приближение.

Важно отметить, что правило 5 разрешает переходы с запрещенные для одноэлектронных спектров. Запрет оказывался следствием правила отбора по четности; в случае одного электрона квантовое число непосредственно определяет четность, поэтому условие означало бы сохранение четности. С другой стороны, для многоэлектронного атома полный орбитальный момент L не имеет прямой связи с четностью, как это имеет место для суммы орбитальных моментов I индивидуальных одноэлектронных волновых функций. Мы видели, например, что в случае двух эквивалентных электронов с заданным все триплетные состояния обладают нечетным L, но четность у всех этих состояний, конечно, положительна. Таким образом, условие совместимо с требованием изменения четности при переходе.

Следует отметить, далее, что хотя правило 9 следует из правил 4 и 6, правило 7 не является следствием правил 3 и 5. Рассмотрим, например, случай положим тогда

Согласно правилам 3 и 5, все четыре перехода были бы возможны, однако правило 7 запрещает переход Правила 4, 6 и 9 оказываются полезными только тогда, когда внешнее поле снимает вырождение по магнитным квантовым числам.

В случае -связи можно доказать следующее правило сумм для интенсивностей переходов. Для совокупности переходов, происходящих из одного мультиплета в другой , сумма интенсивностей линий, соответствующих заданному начальному уровню J, пропорциональна величине . Сумма интенсивностей линий, отвечающих данному конечному уровню пропорциональна

В случае промежуточной или -связи применимы только правила 1, 2, 7, 8 и 9. Правило сумм для интенсивностей уже не имеет места в сформулированном выше виде, однако существуют другие правила сумм [2].

Моменты высших порядков

Если переход запрещен, т. е. дипольный матричный элемент равен нулю, то нужно взять высшие члены разложения экспоненты . Возьмем член второго порядка по положив равным и попытаемся выяснить физический смысл получившегося выражения. Пусть излучение поляризовано вдоль оси , тогда оператор, присутствующий в матричном элементе, пропорционален оператору , который удобно записать в следующем виде:

Первая часть этого выражения пропорциональна полному орбитальному моменту количества движения. Последний в свою очередь пропорционален магнитному (дипольному) моменту атома. Проделав обычное обобщение, с тем чтобы включить спиновый момент количества движения, мы приходим к выводу, что второй

член в мультипольном, разложении соответствует магнитному дипольному излучению, матричный элемент для которого пропорционален

    (13.33)

Так как выражение (13.33) сводится к матричному элементу , который равнялся бы нулю для случая чистой -связи. Иными словами, если бы отсутствовало спин-орбитальное взаимодействие, приводящее к отклонениям от -связи, не было бы и магнитного дипольного излучения. Так как спин-орбитальное взаимодействие разрушает -связь, смешивая состояния с различными L, S, но в общем случае принадлежащие одной и той же конфигурации, то магнитное дипольное излучение имеет место. Однако оно является очень слабым ввиду того, что различие по энергиям двух таких состояний, относящихся к одной и той же конфигурации, довольно невелико.

Ниже приведены правила отбора для магнитного дипольного излучения:

1. Четность должна сохраняться.

4. Переход строго запрещен.

5. (индекс i нумерует все орбитали).

(Для ядер магнитное дипольное излучение весьма существенно. Во-первых, связь в ядре скорее типа чем LS. Но, даже если бы она была -связью, соответствующий матричный элемент был бы пропорционален величине

    (13.34)

где иидексы относятся к протону и нейтрону, соответственно, и . Сохраняющейся величиной является , а не , поэтому магнитные дипольпые переходы оказываются сильными.)

Действуя оставшейся частью операторного выражения (13.32) на волновую функцию приходим к следующему

тождеству:

    (13.35)

Следовательно, матричный элемент от левой части тождества между функциями пропорционален величине

    (13.36)

Это есть электрический квадрупольный момент атома, так что рассматриваемый член приводит к электрическому квадрупольному излучению.

Правила отбора для квадрупольного излучения одноэлектронного атома можно получить следующим образом. По правилам перемножения матриц имеем

Применяя дипольные правила отбора к матричным элементам операторов х и у, мы получаем ; переход запрещен; переход запрещен. Видно также, что четность должна оставаться неизменной. С помощью общих соображений можно получить правила отбора для многоэлектронных атомов [2]. Если взять в только что перечисленных правилах L вместо I и модифицировать одно из них следующим образом: , то результат будет применим и для многоэлектронных атомов. Переход остается запрещенным в случае -связи. Можно также показать, что запрещены переходы или

Мы видели (см. стр. 178), что отношение последовательных интегралов, происходящих от различных членов разложения есть величина порядка если в качестве характерной длины взять боровский радиус Квадрупольное излучение еще более ослабляется из-за того, что оно пропорционально малому по величине среднему по направлениям от произведения Оказалось, что отношение вероятностей переходов для квадрупольного и дипольного излучения обычно меньше, чем , так что время жизни состояний, которые могут затухать только благодаря квадрупольному излучению, превышает сек.

Рассмотрим в качестве примера атом кислорода. Он обладает конфигурацией с возможными состояниями . Основным состоянием является затем с интервалами порядка расположены два других состояния. Дипольные переходы между ними запрещены вследствие того, что все они обладают одинаковыми четностями, так как конфигурация остается неизменной. Квадрупольный переход разрешен и приводит к большому времени жизни. Переход дважды запрещен из-за изменения 5. Так как спин-орбитальное взаимодействие приводит к нарушениям -связи, переход фактически может иметь место за счет магнитного дипольного излучения, но с очень большим временем жизни. В разрядной трубке, заполненной кислородом при разумном давлении, атомы в состоянии распадаются благодаря столкновениям. Но в условиях низкого давления, например в ионосфере, излучение успевает произойти до столкновения. Таково происхождение известной красной линии утренней зари. Кислород возбуждается падающими извне протонами и потом возбужденное состояние распадается с излучением. Часто замечают также запрещенные переходы в солнечной короне и спектрах излучения некоторых туманностей. Сначала полагали, что такие линии соответствуют новому элементу небулию. Боуэн [36] окончательно установил, что подобные линии обусловлены запрещенными переходами сильно ионизованных атомов обычных элементов,

Абсолютные значения вероятностей переходов

Полная вероятность перехода посредством спонтанного излучения из состояния k в состояние определяется выражением

    (12.33)

Запишем его иначе, вводя силу осциллятора,

Просуммируем теперь величины (12.33) или (13.37) по всем состояниям , энергии которых меньше энергии начального состояния k, тогда мы получим полную вероятность (отнесенную к единице времени) того, что состояние k будет опустошено благодаря спонтанному излучению

    (13.38)

Величина, обратная этой, называется временем жизни состояния

    (13.39)

В книге [7] приведены данные для квадратов дипольных моментов, сил осцилляторов и вероятностей переходов для водорода. Обсудим качественно эти результаты.

Сила осциллятора быстро уменьшается с ростом квантового числа п. Чтобы убедиться в этом, напомним, что в определение силы осциллятора входит радиальный интеграл

Если , то функция велика только при малых г. Но при малых , как мы знаем, — [см. (4.34)]. Следовательно, для больших

    (13.40)

С помощью правил сумм мы нашли, что если , то скорее всего превосходит l. Это правило подтверждается. Примеры приведены в табл. 23.

Таблица 23

В случае малых орбитальных квантовых чисел (эксцентричные орбиты боровской теории) переходы в непрерывный спектр происходят чаще, чем из состояний с большим орбитальным числом (с круговых орбит). Примеры значений сил осцилляторов для переходов из состояний в непрерывный спектр указаны в табл. 24.

Таблица 24. ПЕРЕХОДЫ ИЗ СОСТОЯНИЙ nl В НЕПРЕРЫВНЫЙ СПЕКТР

Таблица 25. ВРЕМЕНА ЖИЗНИ РАЗЛИЧНЫХ СОСТОЯНИЙ nl

Вероятность излучения наиболее велика в случае, когда конечным состоянием является основное. Например, вероятности переходов из состояния в различные другие таковы: в состояние в состояние в состояние 55.

Времена жизни сильно, возбужденных состояний больше, чем умеренно возбужденных состояний.

Времена жизни различных состояний nl приведены в табл. 25.

Для атомов щелочных металлов, когда валентный электрон движется под влиянием некулоновского потенциала, первой (так называемой резонансной) линии, соответствующей переходу , отвечает намного большая сила осциллятора, чем линиям, соответствующим переходам из основного состояния в более высокие. Например, в табл. 26 указаны силы осциллятора для соответствующие переходам с уровня, и для сравнения приведены аналогичные величины для Н.

Таблица 26

Отметим, наконец, что в случае атома водорода дипольному переходу соответствует время жизни порядка 2 дней. Состояние может распасться быстрее путем излучения двух квантов, при этом совершается переход в состояние . Время жизни по отношению к этому процессу составляет сек. Энергии каждого из этих двух квантов в отдельности могут быть произвольными, с тем лишь, чтобы сумма их равнялась разности энергий рассматриваемых уровней.