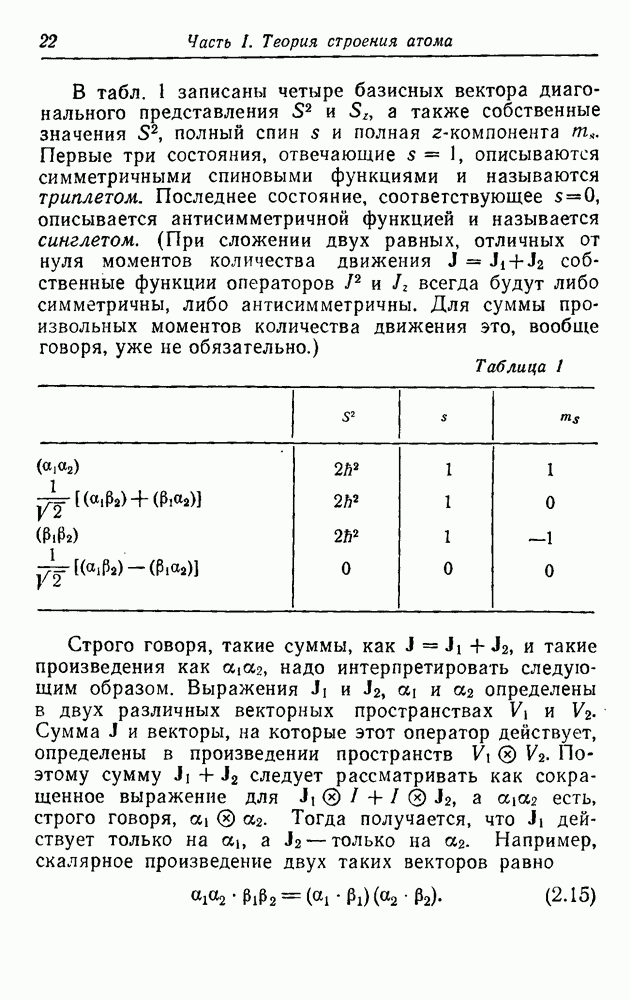
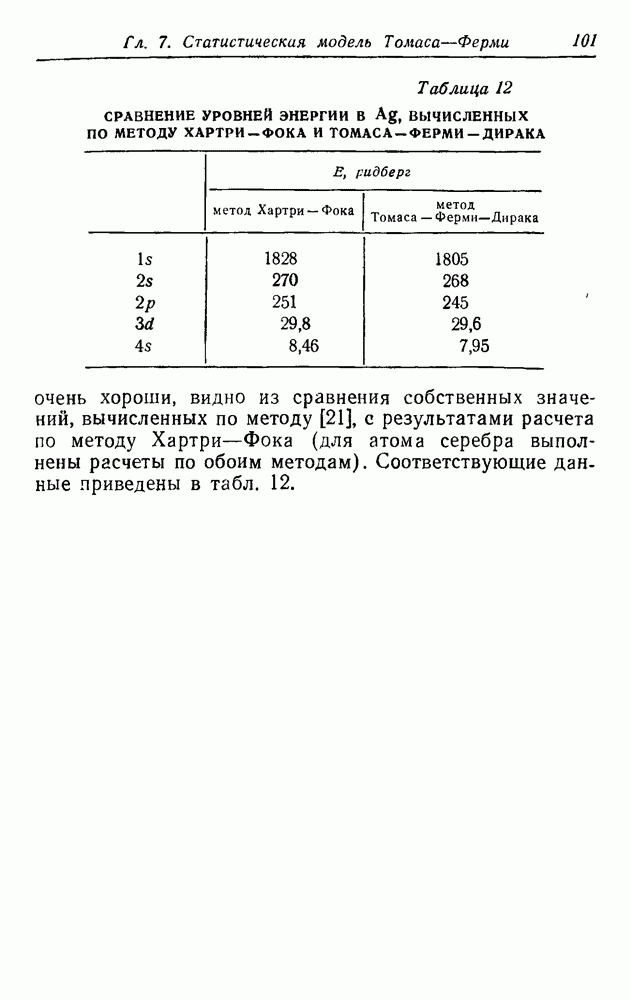
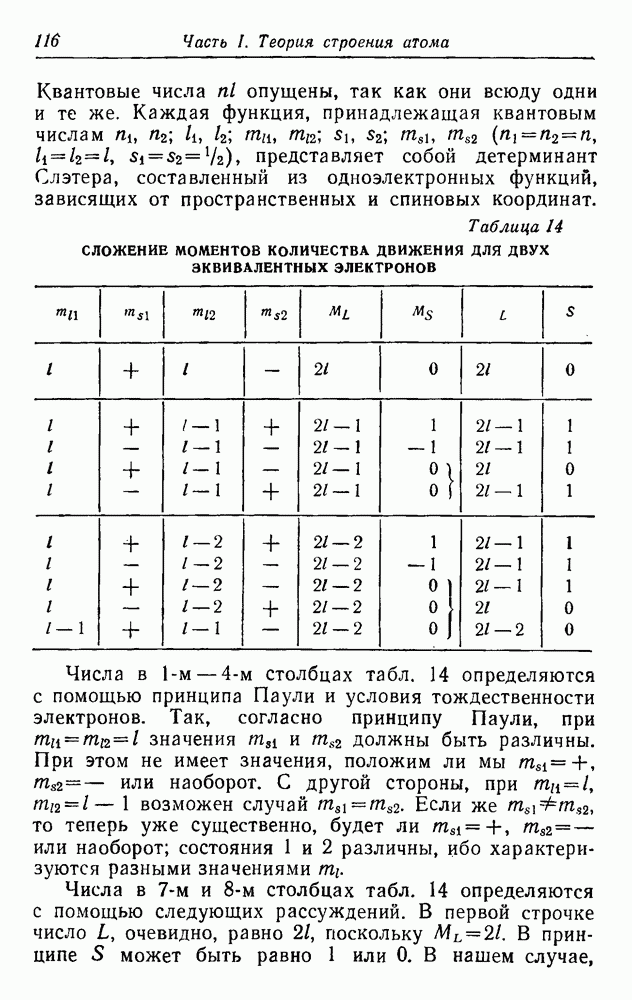
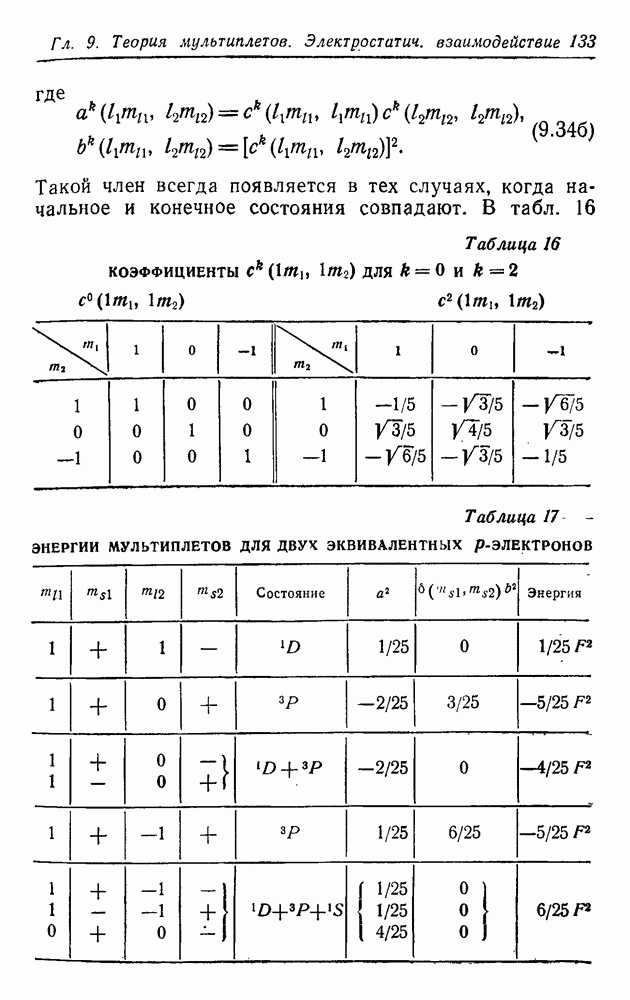
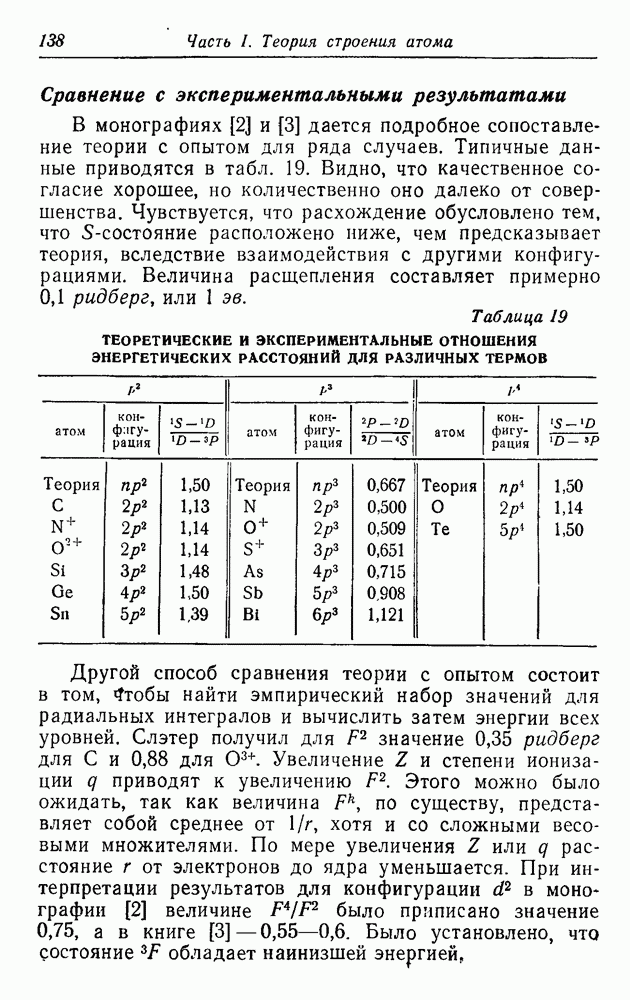
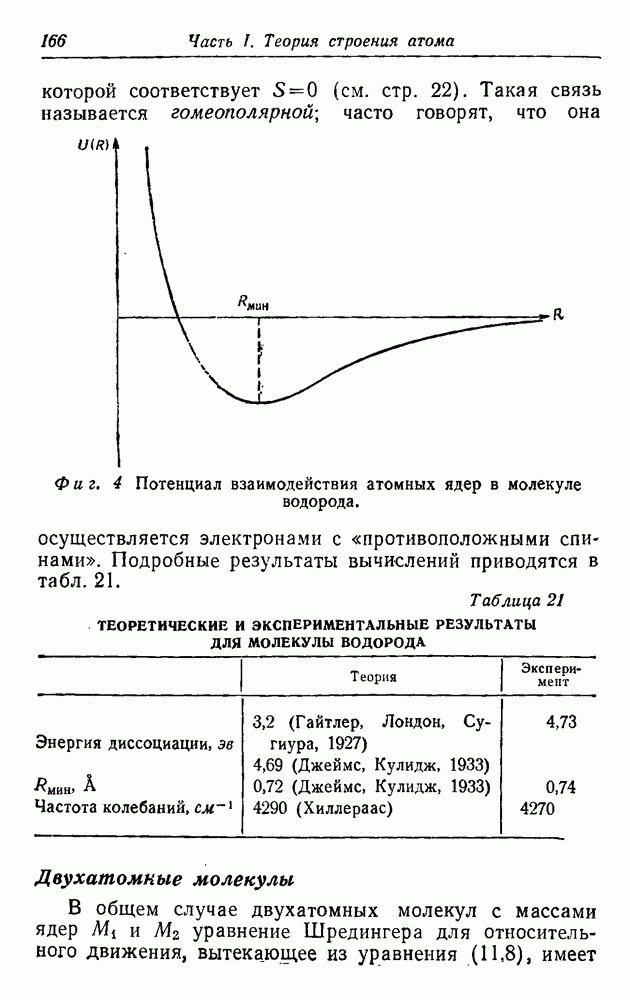
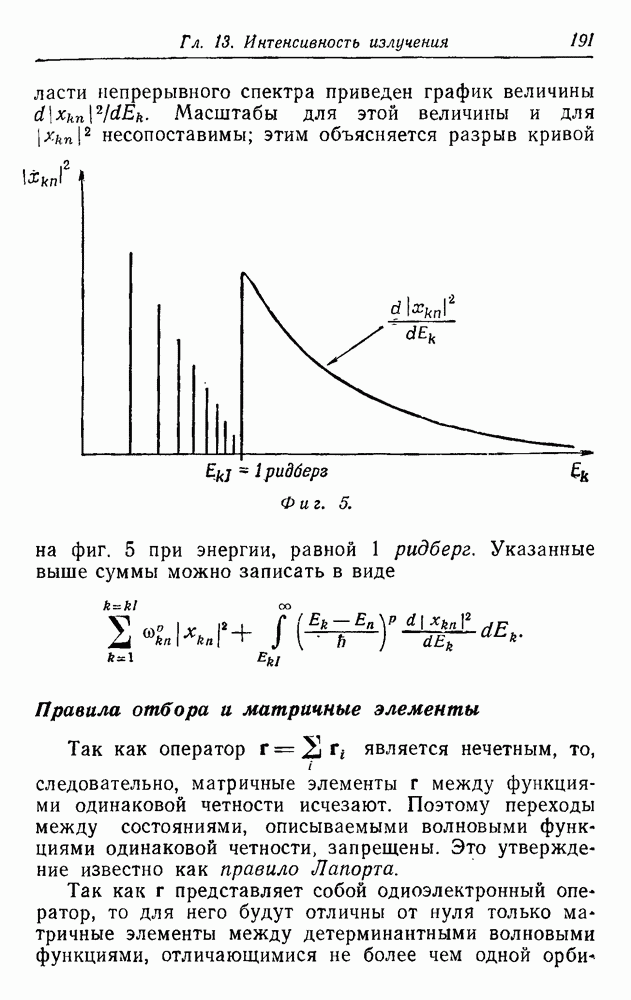
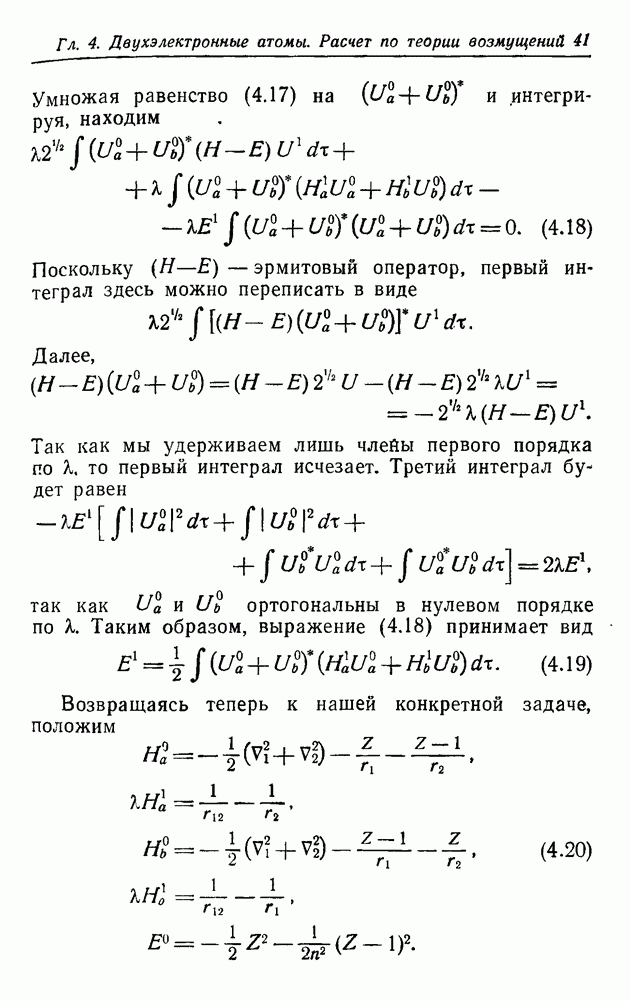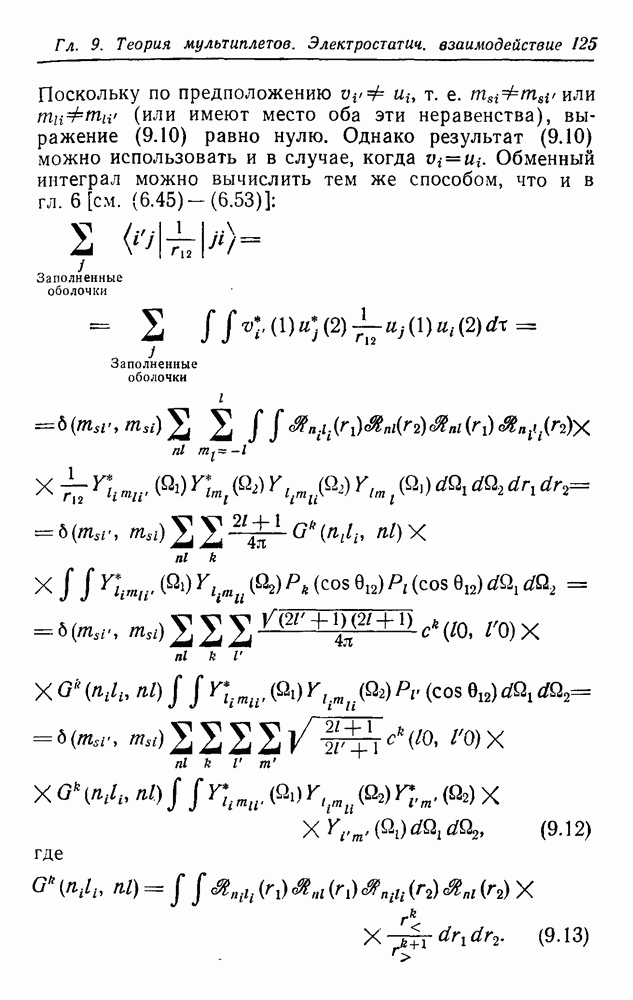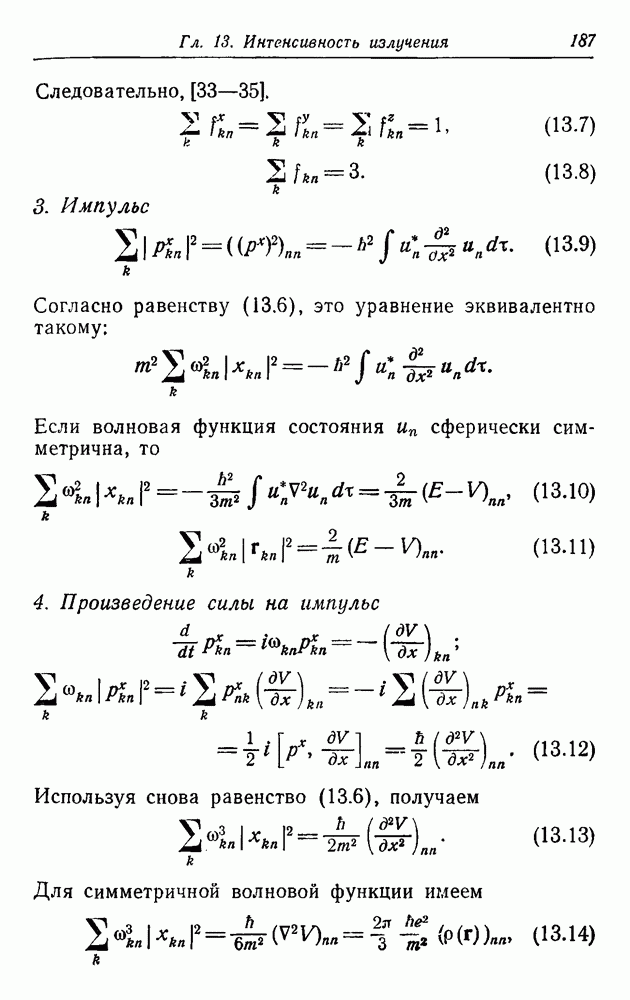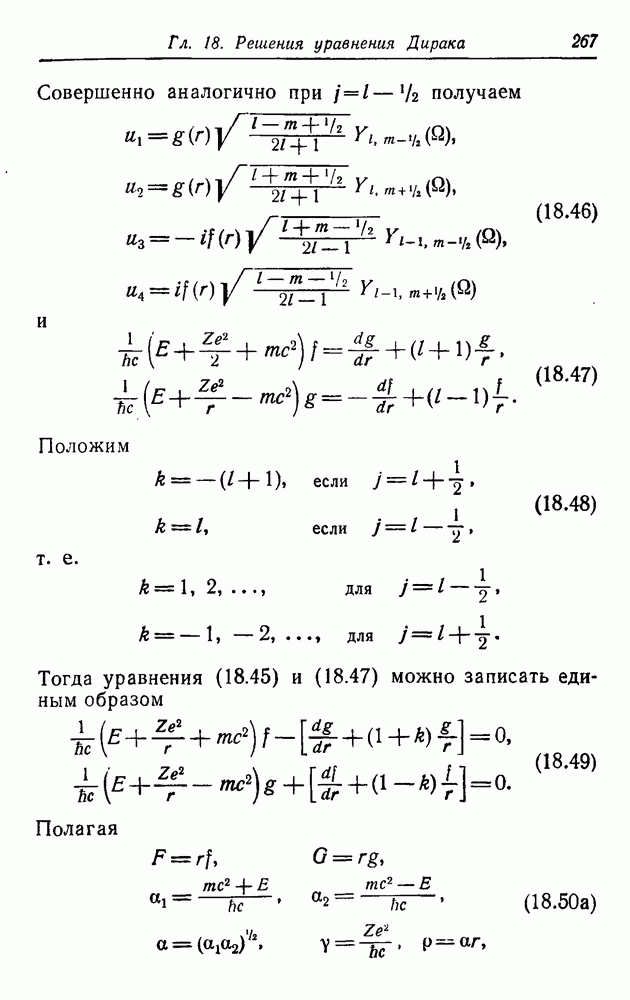| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
18. РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА
Решение для свободных частиц
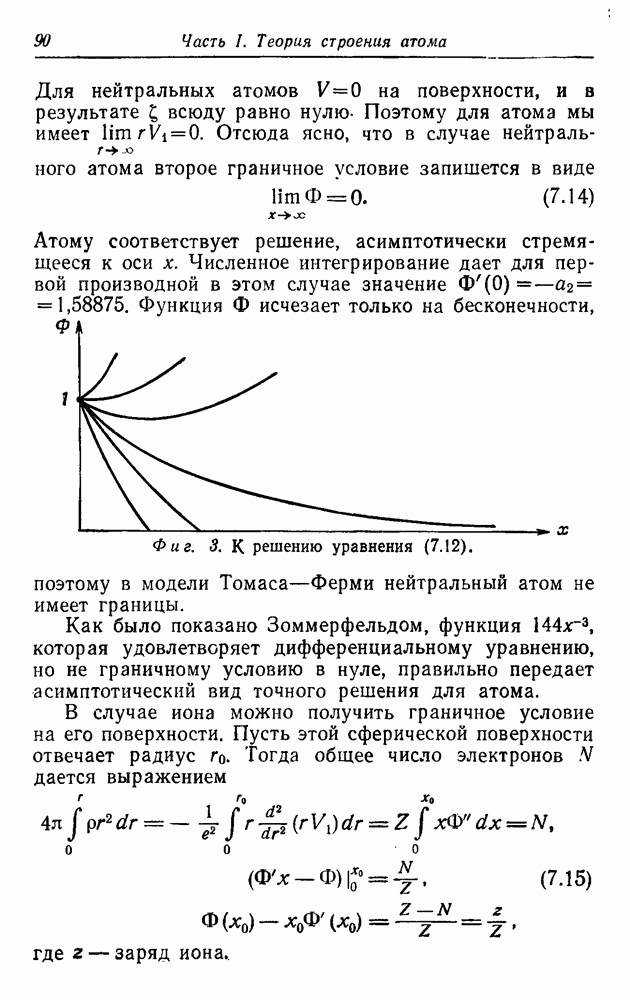
Уравнение Дирака имеет решения в виде плоских волн, т. е. решения, описывающие отдельную частицу в отсутствие взаимодействия. Они имеют вид

Здесь  — четырехкомпонентный столбец, который, в силу (17.19), удовлетворяет уравнению
— четырехкомпонентный столбец, который, в силу (17.19), удовлетворяет уравнению

Это система из четырех однородных алгебраических (а не дифференциальных) уравнений для четырех компонент и. Она обладает нетривиальным решением в том, и только в том случае, когда матрица

не имеет обратной. Поскольку матрица, обратная (18.3), есть

необходимое и достаточное условие существования решения (18.2) имеет вид
 (18.5а)
(18.5а)
При заданном  это уравнение имеет два рещения:
это уравнение имеет два рещения:

Видно, что у уравнения Дирака, так же как у уравнения Клейна — Гордона, есть решения с положительной и отрицательной энергией.
Чтобы получить явное выражение для и, необходимо задаться какой-нибудь определенной формой дираковских матриц. Удобно выбрать представление (17.40). Очевидно, имеются четыре линейно независимых решения; из них два принадлежат  и два
и два  Можно показать, что для
Можно показать, что для  они имеют следующий вид:
они имеют следующий вид:
 (18.6 а)
(18.6 а)
Для  получаем
получаем
 (18.7 а)
(18.7 а)
Здесь и взято в виде

Эта величина не нормирована. Чтобы удовлетворить условию нормировки  каждое
каждое  следует умножить на
следует умножить на

Видно, что каждое решение имеет две компоненты, которые в нерелятивистском предельном случае  порядка
порядка  Они называются малыми компонентами, а две другие — большими компонентами. Для решений с положительной энергией большими
Они называются малыми компонентами, а две другие — большими компонентами. Для решений с положительной энергией большими
компонентами являются  Следует ожидать, что в нерелятивистском предельном случае большие компоненты соответствуют решениям уравнения Шредингера для свободных частиц. Рассматривая выражение (18.1), убеждаемся, что так оно и есть. Для дальнейшего введем оператор
Следует ожидать, что в нерелятивистском предельном случае большие компоненты соответствуют решениям уравнения Шредингера для свободных частиц. Рассматривая выражение (18.1), убеждаемся, что так оно и есть. Для дальнейшего введем оператор

В предельном случае, когда малыми компонентами можно пренебречь, выражения (18.6 а) и (18.7 а) суть собственные функции  с собственным значением
с собственным значением  а (18.66) и
а (18.66) и  -собственные функции
-собственные функции  с собственным значением —1. Ниже мы увидим, что
с собственным значением —1. Ниже мы увидим, что  есть спиновый момент количества движения. Таким образом, четыре решения уравнения Дирака для свободных частиц соответствуют положительной энергии и значениям спина
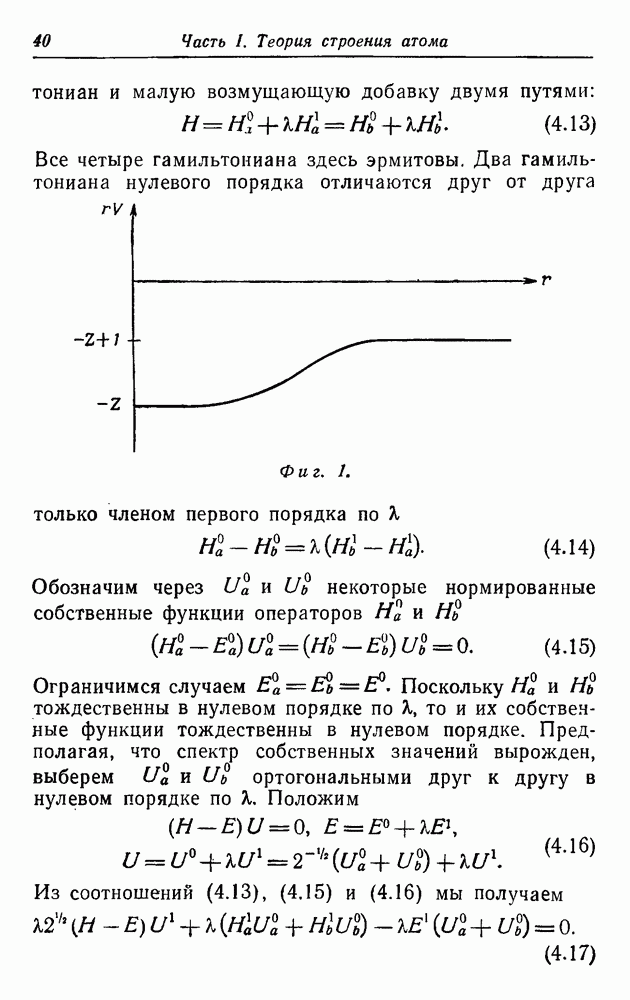
есть спиновый момент количества движения. Таким образом, четыре решения уравнения Дирака для свободных частиц соответствуют положительной энергии и значениям спина  и отрицательной энергии и значениям спина
и отрицательной энергии и значениям спина 
Физическая интерпретация матриц Дирака
Матрица а фигурирует в выражении для потока вероятности  Поэтому нужно ожидать, что
Поэтому нужно ожидать, что  следует интерпретировать как оператор скорости
следует интерпретировать как оператор скорости  . То, что это действительно так, следует из гейзенберговского выражения для производной от оператора по времени.
. То, что это действительно так, следует из гейзенберговского выражения для производной от оператора по времени.
 (18.10)
(18.10)
которое, в силу (17.9), имеет место и в теории Дирака. Тогда

Выражение (18.11) означает, естественно, что матричные элементы операторов в обеих частях равенства
равны, т. е.

Поскольку  собственные значения
собственные значения  равны ±1. Таким образом, собственные значения скорости равны
равны ±1. Таким образом, собственные значения скорости равны  Это весьма примечательный результат, так как из классической теории относительности известно, что частица конечной массы никогда не может иметь скорость, равную скорости света. Больше того, компоненты вектора а не коммутируют друг с другом. Поэтому, когда измеряется скорость в каком-нибудь одном направлении, скорость в двух других направлениях остается совершенно неопределенной. Возникает впечатление, что это свидетельствует о невозможности измерения скорости.
Это весьма примечательный результат, так как из классической теории относительности известно, что частица конечной массы никогда не может иметь скорость, равную скорости света. Больше того, компоненты вектора а не коммутируют друг с другом. Поэтому, когда измеряется скорость в каком-нибудь одном направлении, скорость в двух других направлениях остается совершенно неопределенной. Возникает впечатление, что это свидетельствует о невозможности измерения скорости.
В связи с этими трудностями было высказано предположение, что следует переопределить оператор координаты. Можно перейти к такому представлению матриц Дирака, в котором состояния с положительной и отрицательной энергией не связываются друг с другом. Это так называемое представление Фолди — Вусайзена [41]. Оператор координаты  в этом представлении отличается от оператора координаты в обычном дираковском представлении, которое можно получить из
в этом представлении отличается от оператора координаты в обычном дираковском представлении, которое можно получить из  вого представления посредством унитарного преобразования. Детали расчета можно найти в книге Швебера [42]. Оказывается, оператор
вого представления посредством унитарного преобразования. Детали расчета можно найти в книге Швебера [42]. Оказывается, оператор  в обычном представлении Дирака совпадает с оператором координаты для частиц со спином 1/2, полученным из общих соображений Ньютоном и Вигнером [60].
в обычном представлении Дирака совпадает с оператором координаты для частиц со спином 1/2, полученным из общих соображений Ньютоном и Вигнером [60].
Из формул (18.11) следует, что релятивистская частица со спином  совершает сложное движение. Оно складывается из усредненного трансляционного движения, на которое накладывается колебательное. Шредингер [43] называл его Zitterbewegung (дрожательное движение). Действительно, рассмотрим оператор
совершает сложное движение. Оно складывается из усредненного трансляционного движения, на которое накладывается колебательное. Шредингер [43] называл его Zitterbewegung (дрожательное движение). Действительно, рассмотрим оператор

Здесь прннято во внимание, что  антикоммутирует со всеми матрицами, входящими в Н, за исключением
антикоммутирует со всеми матрицами, входящими в Н, за исключением
самой  . Поскольку Н и
. Поскольку Н и  константы,
константы,
 (18.13)
(18.13)
Интегрируя, получаем
 (18.14)
(18.14)
где  — значение
— значение  при
при  .
.
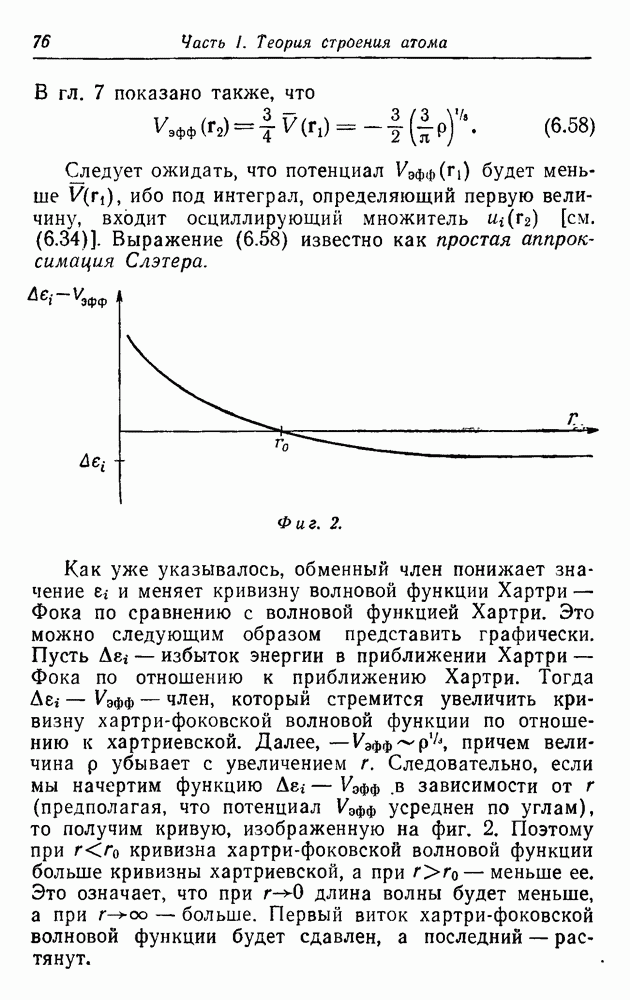
На основании (18.12)
 (18.15)
(18.15)
Замечая, что  имеем
имеем
 (18.16)
(18.16)
Отсюда видно, что «дрожательное движение» представляет собой колебание с частотой  которая равна по меньшей мере
которая равна по меньшей мере  , т. е. очень велика. Конечно, его нельзя наблюдать ни в каком реальном эксперименте. Если рассматривать оператор координаты, о котором шла речь выше в связи с представлением Фолди — Вусайзена; то никакого «дрожательного движения» не получилось бы. Поэтому этот оператор обычно называют оператором средней координаты.
, т. е. очень велика. Конечно, его нельзя наблюдать ни в каком реальном эксперименте. Если рассматривать оператор координаты, о котором шла речь выше в связи с представлением Фолди — Вусайзена; то никакого «дрожательного движения» не получилось бы. Поэтому этот оператор обычно называют оператором средней координаты.
Матрице  не дается никакой физической интерпретации. Однако можно убедиться в справедливости следующих соотношений:
не дается никакой физической интерпретации. Однако можно убедиться в справедливости следующих соотношений:

Смысл этих результатов остается неясным.
Спин
Рассмотрим оператор момента количества движения L и вычислим коммутатор 
 (18.18 а)
(18.18 а)
или

Таким образом, момент количества движения не является более интегралом движения. С другой стороны, существование двух линейно независимых решений, соответствующих заданному значению энергии, указывает, что оператор, коммутирующий с гамильтонианом, должен существовать. Мы покажем, что этот оператор есть
 (18.19)
(18.19)
где оператор а в представлении (17.40 а) и (17.40 в) имеет вид
 (18-20)
(18-20)
Вспоминая правила перестановки матриц Паули а, находим соотношения

а также соотношения, получающиеся отсюда путем циклической перестановки индексов. Тогда
 (18.21 б)
(18.21 б)
и, следовательно,
 (18.22)
(18.22)
Таким образом, оператор (18.19) и в самом деле есть интеграл движения.
Из (18.20) явствует, что собственные значения  равны ±1. Стало быть, (18.22) означает, что имеется сохраняющийся момент количества движения, который представляет собой векторную сумму орбитального момента L и второго члена с собственными значениями
равны ±1. Стало быть, (18.22) означает, что имеется сохраняющийся момент количества движения, который представляет собой векторную сумму орбитального момента L и второго члена с собственными значениями  Таким образом, мы показали, что уравнение Дирака описывает частицы со спином
Таким образом, мы показали, что уравнение Дирака описывает частицы со спином  Все наши предыдущие результаты относительно сложения орбитального и спинового моментов количества движения можно
Все наши предыдущие результаты относительно сложения орбитального и спинового моментов количества движения можно  применить к этому случаю.
применить к этому случаю.
Оператор полного момента количества движения есть  Этот пример иллюстрирует тот факт, что элементарные правила построения операторов с помощью классических динамических переменных (например, замена
Этот пример иллюстрирует тот факт, что элементарные правила построения операторов с помощью классических динамических переменных (например, замена  оператором
оператором  оператором
оператором  в r-представлении) являются недостаточно общими. Вместо этого следует допустить возможность добавления дополнительных членов, которые должны исчезнуть при предельном переходе й
в r-представлении) являются недостаточно общими. Вместо этого следует допустить возможность добавления дополнительных членов, которые должны исчезнуть при предельном переходе й  Так, чтобы получить правильное выражение для оператора момента количества движения из
Так, чтобы получить правильное выражение для оператора момента количества движения из  нам пришлось добавить слагаемое b
нам пришлось добавить слагаемое b  которое обращается в нуль при
которое обращается в нуль при 
Если нежелательно пользоваться каким-нибудь определенным представлением для матриц Дирака, можно положить
 (18.23)
(18.23)
Используя последнее выражение (17.23) для  и замечая, что
и замечая, что  коммутирует со всеми а, получаем
коммутирует со всеми а, получаем
 (18.21 6)
(18.21 6)
На основании определения (18.23) находим
 (18.23 а)
(18.23 а)
где  имеют циклический порядок. Подставляя значения
имеют циклический порядок. Подставляя значения  и
и  , соответствующие специальному представлению и даваемые формулами (17.40 в) и (17.40 г), мы получаем (18.20).
, соответствующие специальному представлению и даваемые формулами (17.40 в) и (17.40 г), мы получаем (18.20).
Уравнение Дирака во внешнем поле
Электромагнитное поле вводится в уравнение Дирака, так же как и уравнение Клейна — Гордона, с помощью градиентно-инвариантной и лоренц-ковариантной замены операторов

т. е.

В результате получается уравнение
 (18.25б)
(18.25б)
Прочие поля можно учесть, добавляя соответствующие потенциалы к  если потенциалы — релятивистские скаляры, или к
если потенциалы — релятивистские скаляры, или к  если это четырехмерные векторы.
если это четырехмерные векторы.
Замена (18.24) не самая общая; возможный добавочный член дается формулой (18.32).
Чтобы получить уравнение второго порядка, похожее по форме на уравнение Клейна — Гордона, умножим (18.256) на  в результате чего получим
в результате чего получим
 (18.26)
(18.26)
Определим тензор
 (18.27)
(18.27)
Замечая на основании (17.18), что

приводим левую часть (18.26) к виду

Коммутатор в последней строке легко вычисляется, если вспомнить, что

и оказывается равным

где  — соответствующая компонента тензора электромагнитного поля. В конце концов получается уравнение
— соответствующая компонента тензора электромагнитного поля. В конце концов получается уравнение

С помощью матрицы в, определяемой формулой (18.23), его можно записать в виде
 (18.31)
(18.31)
Первые два члена в левой части имеются и в уравнении Клейна — Гордона. Два других члена появляются только в теории Дирака и исчезают при 
Последний <лен в левой части (18.30) сам по себе релятивистски инвариантен. В принципе его можно умножить на произвольный фактор  , т. е. прибавить к (18.30) член
, т. е. прибавить к (18.30) член
 (18.32)
(18.32)
Его называют спиновым членом Паули, и он, конечно, приводит к соответствующей модификации первоначального уравнения Дирака. Такая модификация в принципе допустима (поскольку он стремится к нулю при  ), однако она, разумеется, должна усложнить теорию.
), однако она, разумеется, должна усложнить теорию.
Нерелятивистский предельный случай
Имеются два существенно различных метода рассмотрения нерелятивистского предельного случая. В первом методе перемешивание больших и малых компонент  вообще игнорируется. Он пригоден в пренебрежении членами порядка
вообще игнорируется. Он пригоден в пренебрежении членами порядка  Во втором методе члены порядка
Во втором методе члены порядка  удерживаются, и производится перестройка больших компонент
удерживаются, и производится перестройка больших компонент 
Чтобы получить первое приближение, положим

где

Тогда (18.31) примет вид
 (18.33)
(18.33)
Оценим теперь член, содержащий  . Как видно из (18.11), математическое ожидание а есть
. Как видно из (18.11), математическое ожидание а есть  Для электрона, который движется в системе размера а,
Для электрона, который движется в системе размера а,  порядка
порядка  . Поэтому
. Поэтому

и членом с электрическим полем следует пренебречь. Этот член необходим для лоренц-ковариантности, но в нерелятивистском приближении он не играет роли. Таким образом,

Член с  имеет форму энергии магнитного дипольного взаимодействия. В обычном представлении
имеет форму энергии магнитного дипольного взаимодействия. В обычном представлении

и мы заключаем, что магнитный момент электрона есть  Этот вывод подтверждает гипотезу Уленбека — Гаудсмита и дает правильное гиромагнитное отношение.
Этот вывод подтверждает гипотезу Уленбека — Гаудсмита и дает правильное гиромагнитное отношение.
Вопрос о поправках, вносимых квантовой электродинамикой, выходит за рамки данного рассмотрения. Мы укажем лишь, что взаимодействие заряженной частицы со своим собственным полем дает поправочный множитель g к магнитному моменту, который оказывается равным

В точности такое значение магнитного момента было обнаружено на опыте. Другое наблюдаемое следствие самодействия электрона есть лэмбовский сдвиг.
Теория Дирака не дает правильного значения магнитного момента протона. Его можно получить, добавляя в уравнения Дирака первого порядка так называемый член Паули

который не нарушает релятивистской инвариантности уравнения. Константа К подбирается таким образом, чтобы получался правильный результат. Произвольность такой процедуры делает ее неудовлетворительной. Считается, что добавочный магнитный момент протона физически обусловлен взаимодействием с мезонным полем, однако попытки построить количественную теорию до сих пор были безуспешными.
Перестройка больших компонент начинается с уравнения первого порядка (18.25 а). Пишем в (18.25 а)
 (18.35)
(18.35)
где  двухкомпонентные функции. Если воспользоваться явным выражением для матриц Дирака, уравнение (18.25 а) примет вид
двухкомпонентные функции. Если воспользоваться явным выражением для матриц Дирака, уравнение (18.25 а) примет вид
 (18.36)
(18.36)
Это в свою очередь эквивалентно двум связанным уравнениям:
 (18.37 а)
(18.37 а)
Здесь  — двухрядная матрица Паули, и каждая из величин
— двухрядная матрица Паули, и каждая из величин  имеет по две компоненты. Из уравнения (18.376) следует, что
имеет по две компоненты. Из уравнения (18.376) следует, что
 (18.38 а)
(18.38 а)
Полагая  получаем
получаем

В нерелятивистском предельном случае

Отсюда
 (18.39)
(18.39)
т. е. четырехкомпонентное решение  имеет две большие компоненты
имеет две большие компоненты  и две малые компоненты
и две малые компоненты  как и в случае для свободных частиц. Далее, подставляя в (18.37 а) точное выражение (18.386), перегруппировывая члены и полагая
как и в случае для свободных частиц. Далее, подставляя в (18.37 а) точное выражение (18.386), перегруппировывая члены и полагая  получаем
получаем

Аппроксимируем правую часть (18.40), удерживая только члены наинизшего порядка в разложении по
степеням  . Тогда справедливы следующие соотношения:
. Тогда справедливы следующие соотношения:

Если предположить сферическую симметрию V, то из уравнения (18.40) следует

где

Наконец, полагая в поправочном члене  , получаем
, получаем

Два первых слагаемых в правой части (18.416) те же, что и в нерелятивистском уравнении Шредингера. Третье слагаемое происходит от второго члена в разложении Е по степеням  ,
,

Следующее слагаемое классического аналога не имеет. Наконец, последнее слагаемое описывает энергию спин-орбитальной связи с учетом множителя Томаса  (см. стр. 145).
(см. стр. 145).
Процедура решения получившегося уравнения заключается в следующем. Сначала решается нерелятивистское уравнение Шредингера для двух компонент затем составляется их линейная комбинация, соответствующая
определенным допустимым значениям  и S, и, наконец, члены
и S, и, наконец, члены

и спин-орбитальное взаимодействие рассматриваются как возмущение.
Точное решение уравнения Дирака для кулоновского потенциала
Решим уравнение Дирака для кулоновского поля. Будем пользоваться собственно дираковским представлением, т. е. решим четыре уравнения (18.37 а) и (18.37 б) при  Полагая
Полагая

получаем

Чтобы найти решение, воспользуемся следующим обстоятельством. Если рассматривать только большие компоненты, т. е. приравнять малые компоненты нулю, то коммутатор [1, Н], пропорциональный  также будет равен нулю, поскольку оператор а связывает большие и малые компоненты. Таким образом,
также будет равен нулю, поскольку оператор а связывает большие и малые компоненты. Таким образом,  будет собственной функцией 1. Она должна содержать одну компоненту со спином, направленным вверх, и одну — со спином, направленным вниз. Разумеется, операторы
будет собственной функцией 1. Она должна содержать одну компоненту со спином, направленным вверх, и одну — со спином, направленным вниз. Разумеется, операторы  являются интегралами движения. Поэтому для
являются интегралами движения. Поэтому для
 полагаем
полагаем

Здесь в отличие от нерелятивистского рассмотрения Паули  есть пока произвольная радиальная функция, а не решение нерелятивистского радиального уравнения Шредингера.
есть пока произвольная радиальная функция, а не решение нерелятивистского радиального уравнения Шредингера.
Чтобы определить малые компоненты, заметим, что они даются соотношением
 (18.38 а)
(18.38 а)
Оператор, переводящий большие компоненты в малые, нечетен (ибо нечетен оператор  , в то время как все остальные четны). Далее, он коммутирует с j. Поэтому функция
, в то время как все остальные четны). Далее, он коммутирует с j. Поэтому функция  должна принадлежать тому же значению
должна принадлежать тому же значению  что и
что и  но другому значению I. Единственное другое значение орбитального момента количества движения, соответствующее
но другому значению I. Единственное другое значение орбитального момента количества движения, соответствующее  есть
есть  Поэтому, вспомнив значения коэффициентов Клебша — Гордана, положим
Поэтому, вспомнив значения коэффициентов Клебша — Гордана, положим
 (18.44)
(18.44)
где  — некоторая радиальная функция. Подставляя (18.43) и (18.44) в (18.42), находим связь между
— некоторая радиальная функция. Подставляя (18.43) и (18.44) в (18.42), находим связь между  при
при 
 (18.45)
(18.45)
Совершенно аналогично при  получаем
получаем

и
 (18.46)
(18.46)
Положим

т. е.
 (18.48)
(18.48)
Тогда уравнения (18.45) и (18.47) можно записать единым образом

Полагая

получаем
 (18.50б)
(18.50б)
Будем искать решения в освященном временем виде степенных рядов. Прежде всего положим
 (18.51)
(18.51)
Для функций  получим уравнения
получим уравнения

Представим, далее,  в виде
в виде
 (18.53)
(18.53)
Мы увидим, что функции f и g нельзя выбрать так, чтобы они были всюду конечными. Потребуем поэтому, чтобы оставался конечным хотя бы интеграл от плотности вероятности
 (18.54)
(18.54)
Из этого уравнения вытекает, что  . Подставляя ряды (18.53) в (18.52) и приравнивая коэффициенты при одинаковых степенях р, получаем
. Подставляя ряды (18.53) в (18.52) и приравнивая коэффициенты при одинаковых степенях р, получаем
 (18.55)
(18.55)
В частности, при 
 (18,56)
(18,56)
Это уравнение имеет нетривиальное решение в том, и только в том, случае, когда
 (18.57 а)
(18.57 а)
Рассмотрим сначала отрицательный корень. Для малых  подынтегральное выражение в (18.54) пропорционально
подынтегральное выражение в (18.54) пропорционально  поэтому должно быть
поэтому должно быть  Своего наименьшего значения s достигает при
Своего наименьшего значения s достигает при  при этом должно быть
при этом должно быть  отрицательный корень недопустим ни при каком Z. Ограничиваясь значениями
отрицательный корень недопустим ни при каком Z. Ограничиваясь значениями  выберем положительный корень
выберем положительный корень 
 (18.57 б)
(18.57 б)
При  функции f, g обращаются в бесконечность; однако интеграл (18.54) остается конечным.
функции f, g обращаются в бесконечность; однако интеграл (18.54) остается конечным.
Легко видеть, что рекуррентные соотношения (18.55) определяют функцию, которая при больших  ведет себя как
ведет себя как  поэтому, чтобы выполнялось условие (18.54), ряды должны обрываться. Предположим, что это имеет место при
поэтому, чтобы выполнялось условие (18.54), ряды должны обрываться. Предположим, что это имеет место при  . Тогда из (18.55) следует
. Тогда из (18.55) следует
 (18.58)
(18.58)
Умножая первое из уравнений (18.55) на а, а второе на  и вычитая одно из другого, получаем
и вычитая одно из другого, получаем
 (18.59)
(18.59)
Полагая здесь  и используя условие (18.58), находим
и используя условие (18.58), находим

откуда
 (18.60 а)
(18.60 а)
Замечая, что  , получаем
, получаем
 (18.60 в)
(18.60 в)
Из формулы (18.606) видно, что отрицательные значения  также приемлемы. Однако при
также приемлемы. Однако при  равенства (18.56) и (18.58) дают
равенства (18.56) и (18.58) дают
 (18.61)
(18.61)
Поскольку  знак первого выражения для
знак первого выражения для  совпадает со знаком k, второе же выражение всегда отрицательно. Поэтому при
совпадает со знаком k, второе же выражение всегда отрицательно. Поэтому при  может быть только отрицательным, т. е.
может быть только отрицательным, т. е.  Выражение (18.60 в) можно разложить в ряд по степеням
Выражение (18.60 в) можно разложить в ряд по степеням 

Здесь 
Видно, что теория Дирака приводит к случайному вырождению по  состояния с одним и тем же значением
состояния с одним и тем же значением  и разными
и разными  отвечают одинаковой энергии. Это вырождение устраняется лэмбовским сдвигом, обусловленным взаимодействием электрона со своим собственным полем. Для
отвечают одинаковой энергии. Это вырождение устраняется лэмбовским сдвигом, обусловленным взаимодействием электрона со своим собственным полем. Для  этот эффект на порядок меньше расщепления тонкой структуры, для
этот эффект на порядок меньше расщепления тонкой структуры, для  — на два порядка меньше. Например, согласно теории Дирака, значению
— на два порядка меньше. Например, согласно теории Дирака, значению  соответствуют два состояния одинаковой энергии:
соответствуют два состояния одинаковой энергии:  сверхтонкое расщепление между ними и состоянием
сверхтонкое расщепление между ними и состоянием  составляет около
составляет около  . Благодаря лэмбовскому сдвигу состояние s, оказывается примерно на
. Благодаря лэмбовскому сдвигу состояние s, оказывается примерно на  выше, чем
выше, чем  Энергия связи составляет
Энергия связи составляет  так что мы и в самом деле имеем дело с «тонкой» структурой.
так что мы и в самом деле имеем дело с «тонкой» структурой.
Решения с отрицательной энергией
Мы видели, что как в теории Клейна — Гордона, так и в теории Дирака дозволены состояния с положительной энергией  и состояния с отрицательной энергией
и состояния с отрицательной энергией
 . В классической теории также существуют решения с отрицательной энергией. Однако
. В классической теории также существуют решения с отрицательной энергией. Однако  можно исключить с помощью соображений физической непрерывности: классическая частица не может перейти из состояния с положительной энергией в состояние с отрицательной энергией, не проходя через состояния с промежуточной энергией. Поэтому отбрасывание состояний с отрицательной энергией эквивалентно начальному условию, согласно которому «вначале» все частицы имели положительную энергию.
можно исключить с помощью соображений физической непрерывности: классическая частица не может перейти из состояния с положительной энергией в состояние с отрицательной энергией, не проходя через состояния с промежуточной энергией. Поэтому отбрасывание состояний с отрицательной энергией эквивалентно начальному условию, согласно которому «вначале» все частицы имели положительную энергию.
Совершенно свободная отдельная квантовая частица также не совершает квантовых переходов. Однако совершенно свободных частиц не бывает, и переходы всегда происходят вследствие взаимодействия с полем излучения или иным образом. Можно, например, вычислить, что для электрона, связанного в атоме водорода, излучательный переход в состояние с отрицательной энергией произойдет примерно за  . Коль скоро переход произошел, электрон будет быстро «падать» в направлении бесконечной отрицательной энергии. Такой вывод, очевидно, противоречит опыту.
. Коль скоро переход произошел, электрон будет быстро «падать» в направлении бесконечной отрицательной энергии. Такой вывод, очевидно, противоречит опыту.
Дирак предложил считать состояния с отрицательной энергией занятыми. Тогда переходы в них запрещены принципом Паули. Предполагалось, что электроны, занимающие состояния с отрицательной энергией, не создают гравитационных или электромагнитных эффектов. Иными словами, согласно Дираку, в состоянии вакуума все состояния с отрицательной энергией заполнены. Иногда одно или несколько состояний с отрицательной энергией могут оказаться пустыми. Отсутствие отрицательно заряженного электрона должно проявиться как присутствие положительно заряженного электрона, т. е. позитрона. Когда Паули в 1932 г. в своей статье (44] рассматривал такую интерпретацию состояний с отрицательной энергией, он отверг ее на том основании, что в то время отсутствовали экспериментальные свидетельства в пользу существования позитронов. Однако к тому времени, когда статья появилась в печати (1933 г.), позитрон уже был открыт  дерсоном (55] (1932 г.), и теория Дирака была реабилитирована.
дерсоном (55] (1932 г.), и теория Дирака была реабилитирована.
Представление о «море электронов с отрицательной энергией» позволяет вычислить вероятность образования пары в электрическом поле ядра — надо лишь вычислить вероятность перехода электрона из состояния с отрицательной в состояние с положительной энергией.
Кажущуюся асимметрию в рассмотрении электронов и позитронов можно устранить. Это было сделано Гейзенбергом [45] и Крамерсом [46].
Следует заметить, что в применении к уравнению Клейна — Гордона подобный прием не проходит, так как частицы со спином нуль не подчиняются принципу Паули. Паули и Вейсскопф [38] показали, что энергия квантованного поля всегда положительна. Параметр Е в волновом уравнении положителен для положительно заряженных частиц и отрицателен для отрицательно заряженных. То же относится и к плотности заряда.
Теория возмущений
Из общей структуры теории Дирака ясно, что как стационарная, так и нестационарная теории возмущений формально строятся так же, как и в нерелятивистской теории Шредингера. Разница состоит лишь в том, что матричные элементы вычисляются теперь между спинорами, а не между однокомпонентными (скалярными) волновыми функциями. Рассмотрим рассеяние свободных частиц постоянным потенциалом V.
Вероятность рассеяния в единицу времени дается известной формулой
 (18.63)
(18.63)
где

Начальная волновая функция свободных частиц есть
 (18.65)
(18.65)
где 4-компонентный спинор  не зависит от
не зависит от  . Волновая функция конечного состояния имеет вид
. Волновая функция конечного состояния имеет вид
 (18.66)
(18.66)
где  не зависит от
не зависит от  . Таким образом,
. Таким образом,
 (18.67)
(18.67)
С точностью до множителя  это — то же выражение, что и в нерелятивистском борновском приближении.
это — то же выражение, что и в нерелятивистском борновском приближении.
Вычислим величину  . Обычно не интересуются конечными состояниями с какой-нибудь определенной проекцией спина, поэтому следует просуммировать по всем конечным спиновым состояниям. Далее, может оказаться необходимым взять лоловину суммы по начальным спиновым состояниям. Это усреднение по начальным значениям спина следует произвести, если начальное состояние неполяризовано.
. Обычно не интересуются конечными состояниями с какой-нибудь определенной проекцией спина, поэтому следует просуммировать по всем конечным спиновым состояниям. Далее, может оказаться необходимым взять лоловину суммы по начальным спиновым состояниям. Это усреднение по начальным значениям спина следует произвести, если начальное состояние неполяризовано.
Проще всего вычислять такие суммы с помощью проекционных операторов Казимира. Следует заметить, что, рассматривая упругое рассеяние, мы не можем преобразовывать суммы с помощью условия полноты, ибо суммирование производится не по всем возможным квантовым состояниям. В частности, как начальная, так и конечная энергии должны быть положительны. Введем оператор
 (18.68)
(18.68)
Заметим, что выражение
 (18.69)
(18.69)
равно  или 0 в зависимости от того, принадлежит ли и состояниям с положительной или с отрицательной энергией. Представим Р в следующем виде:
или 0 в зависимости от того, принадлежит ли и состояниям с положительной или с отрицательной энергией. Представим Р в следующем виде:

Отсюда

Эти две суммы равны друг другу, поскольку проекционные операторы при действии на функции состояний с отрицательной энергией дают нуль. Заметим далее, что
 (18.72)
(18.72)
Величины  в этих двух операторах одинаковы, так как рассеяние упругое. Теперь, суммируя по конечным состояниям, мы уже можем воспользоваться условием полноты.
в этих двух операторах одинаковы, так как рассеяние упругое. Теперь, суммируя по конечным состояниям, мы уже можем воспользоваться условием полноты.
 (18.73)
(18.73)
Поскольку суммирование производится здесь по полной системе биспиноров  мы можем взять любую полную систему. Выбирая ее в виде
мы можем взять любую полную систему. Выбирая ее в виде

получаем
 (18.74)
(18.74)
Расписывая скалярное произведение и пользуясь тем обстоятельством, что

находим окончательно
 (18.75)
(18.75)
где

Итак, сечение рассеяния в теории Дирака отличается от результатов нерелятивистской теории множителем.
 (18.76)
(18.76)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Часть I. ТЕОРИЯ СТРОЕНИЯ АТОМА
- 1. УРАВНЕНИЕ ШРЕДИНГЕРА И ПРИБЛИЖЕННЫЕ МЕТОДЫ ЕГО РЕШЕНИЯ
- 2. ИНТЕГРАЛЫ ДВИЖЕНИЯ
- 3. ТОЖДЕСТВЕННОСТЬ ЧАСТИЦ И СИММЕТРИЯ
- 4. ДВУХЭЛЕКТРОННЫЕ АТОМЫ. РАСЧЕТ ПО ТЕОРИИ ВОЗМУЩЕНИЙ
- 5. ДВУХЭЛЕКТРОННЫЕ АТОМЫ. РАСЧЕТ ВАРИАЦИОННЫМ МЕТОДОМ
- 6. САМОСОГЛАСОВАННОЕ ПОЛЕ
- 7. СТАТИСТИЧЕСКАЯ МОДЕЛЬ ТОМАСА—ФЕРМИ
- 8. ТЕОРИЯ МУЛЬТИПЛЕТОВ. СЛОЖЕНИЕ МОМЕНТОВ
- 9. ТЕОРИЯ МУЛЬТИПЛЕТОВ. ЭЛЕКТРОСТАТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ
- 10. ТЕОРИЯ МУЛЬТИПЛЕТОВ. МАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ
- 11. МОЛЕКУЛЫ
- 12. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ ИЗЛУЧЕНИЯ
- 13. ИНТЕНСИВНОСТЬ ИЗЛУЧЕНИЯ
- 14. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
- 15. СТОЛКНОВЕНИЯ АТОМОВ С ЗАРЯЖЕННЫМИ ЧАСТИЦАМИ
- Часть II. РЕЛЯТИВИСТСКИЕ ТЕОРИИ
- 16. УРАВНЕНИЕ КЛЕЙНА—ГОРДОНА
- 17. УРАВНЕНИЕ ДИРАКА. ФОРМАЛЬНАЯ ТЕОРИЯ
- 18. РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА
- Часть III. ВВЕДЕНИЕ В ТЕОРИЮ ПОЛЯ
- 19. КВАНТОВАНИЕ ПОЛЯ
- 20. ВТОРИЧНОЕ КВАНТОВАНИЕ НЕСКОЛЬКИХ ПОЛЕЙ ЧАСТИЦ
- 21. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ. КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- ЛИТЕРАТУРА