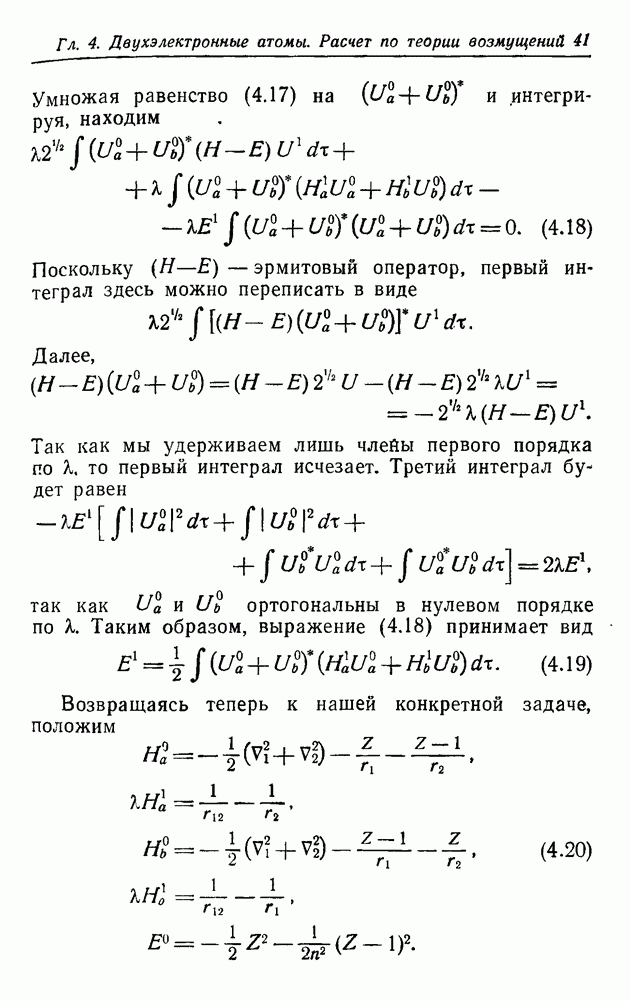4. ДВУХЭЛЕКТРОННЫЕ АТОМЫ. РАСЧЕТ ПО ТЕОРИИ ВОЗМУЩЕНИЙ

Будем решать уравнение (1.4) для двух электронов с помощью теории возмущений. В теории атома удобно пользоваться так называемыми атомными единицами (Хартри). При этом масса и заряд измеряются в единицах массы покоя и заряда электрона, длины — в единицах первого боровского радиуса атома водорода, . В этих единицах уравнение (1.4) для двух электронов принимает вид

Это уравнение не допускает разделения переменных. Так как гамильтониан не содержит спиновых переменных, то полная волновая функция , где U — пространственная, — спиновая часть волновой функции. Функция должна быть антисимметрична при перестановке двух электронов. Гамильтониан симметричен при перестановке пространственных координат. Таким образом, можно выбрать пространственные функции либо полностью симметричными, либо антисимметричными. В первом случае мы имеем пара-состояния, во втором — орто-состояния

Из общей антисимметрии волновой функции опре деляются свойства симметрии спиновой функции

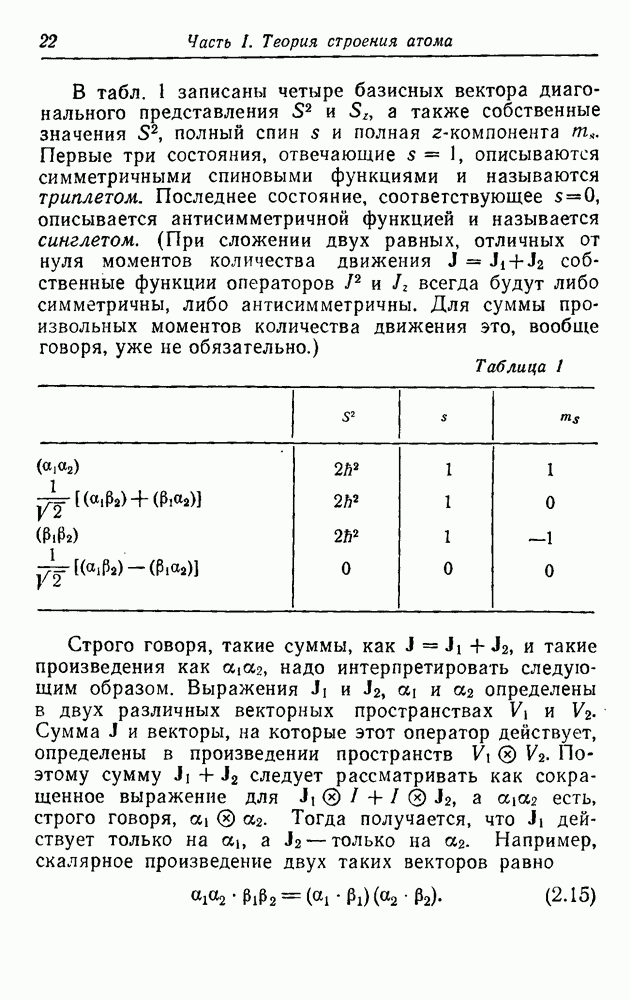
Из табл. 1 видим, что единственная антисимметричная спиновая функция двух электронов представляет собой синглет

Существуют три линейно независимые симметричные спиновые (орто-)функции. В качестве их удобно выбрать собственные функции операторов

Так как существуют три такие функции, орто-состояния называются также триплетными.

Для использования теории возмущений полный гамильтониан, фигурирующий в уравнении (4.1), можно записать в виде причем

Степени параметра к отмечают порядки возмущения. Критерий выбора величин состоит в том, чтобы уравнение Шредингера с оператором можно было явно решить и вместе с тем влияние возмущения было мало. Если через обозначить любые два нормированные решения одночастичного уравнения

то волновое уравнение нулевого приближения

решается подстановкой

Поскольку потенциал обладает центральной симметрией, решение (4.6) можно представить в виде

где есть присоединенный полином Лежандра. Далее, если функция имеет кулоновский вид, то

По излагаемым ниже причинам для гелия (и гелиеподобных ионов) практическое значение имеют лишь такие состояния системы, при которых по крайней мере один электрон находится в основном состоянии. Дело в том, что энергия любого состояния атома Не, в котором оба электрона возбуждены, выше энергии основного состояния иона плюс свободный электрон. Поэтому такие дважды возбужденные состояния быстро распадутся на ион и свободный электрон; иначе говоря, они попадают в область непрерывного спектра. Соответственно мы будем рассматривать лишь случай, когда один электрон находится в состоянии . Состояния таких атомов описываются лишь тремя квантовыми числами и указанием на орто- или пара-состояние.

Симметризованные и нормированные волновые функции нулевого приближения будут

Здесь знак относится к пара-, а знак к орто-состояниям. Индекс 1 обозначает основное состояние. Видим, что если оба электрона находятся в основном состоянии, то волновая функция нулевого приближения в орто-случае тождественно обращается в нуль, так что мы не получаем решения. Отсюда следует, что низшее по энергии состояние должно быть пара-состоянием. Вообще для орто-состояний функция всякий раз, когда два электрона берутся в одной точке, т. е. Для пара-состояний это не так. Поэтому

вероятность того, что два электрона очень близки друг к другу, для орто-состояний много меньше, чем для пара-состояний. Это в свою очередь означает, что энергия пара-состояний должна быть меньше, чем энергия орто-состояний. Кроме того, следует ожидать, что оптические переходы из орто-состояний в пара-состояния (или наоборот) будут запрещены по следующей причине. Оператор электрического дипольного момента и пространственная волновая функция пара-состояния не изменяются при перестановке двух электронов, в то время как пространственная волновая функция орто-состояния меняет знак. В матричный элемент перехода входит интеграл по пространственным координатам обоих электронов. Из соображений симметрии этот интеграл должен обращаться в нуль.

Суммируем сказанное. Схема уровней гелия или ионов с двумя электронами состоит из двух систем уровней, оптически не связанных друг с другом, причем одна система содержит триплетные, а другая — синглетные уровни. Основным является пара-состояние. Для всех возбужденных уровней собственные значения энергии пара-состояний больше, чем соответствующих орто-состояний.

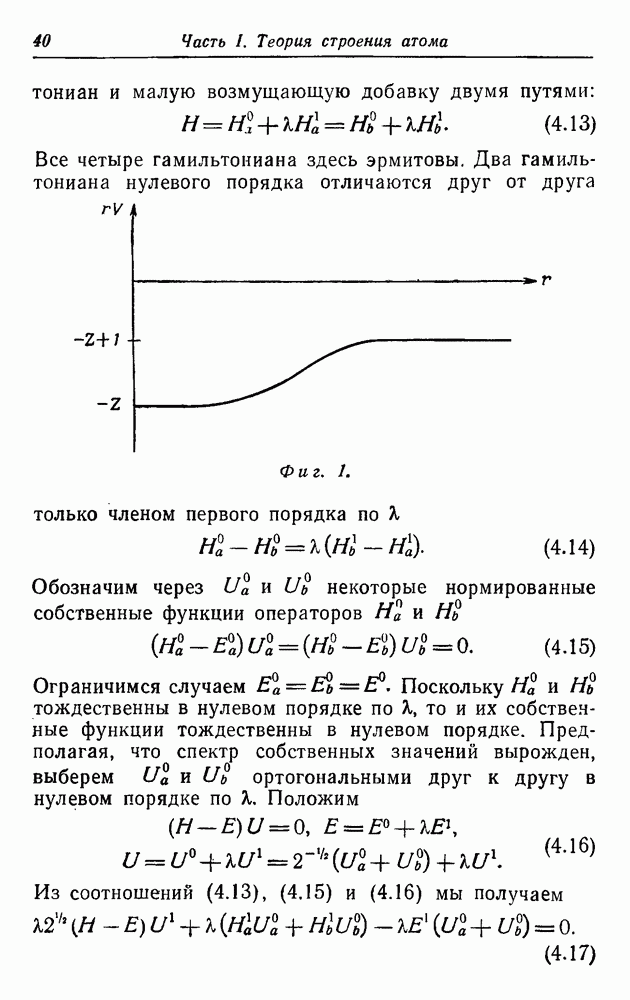
Специализируем теперь вид операторов входящих в (4.5), следуя Гейзенбергу [10]. Разумное предположение относительно эффективного одночастичного потенциала состоит в следующем. При достаточно малых первый электрон «чувствует» весь заряд ядра Z. Для достаточно больших заряд ядра экранируется вторым электроном и первый «чувствует» заряд . На фиг. 1 схематически изображен потенциал, описывающий эту ситуацию. Следуя Гейзенбергу, мы предположим теперь, что первый электрон находится в основном состоянии, а второй — в возбужденном. Тогда

При этом два электрона рассматриваются несимметрично, и необходимо видоизменить формулы первого порядка теории возмущений на предмет учета этой асимметрии. Разобьем гамильтониан Н на нулевой гамильтониан

и малую возмущающую добавку двумя путями:

Все четыре гамильтониана здесь эрмитовы.

Фиг. 1

Два гамильтониана нулевого порядка отличаются друг от друга только членом первого порядка по А,

Обозначим через некоторые нормированные собственные функции операторов

Ограничимся случаем . Поскольку и тождественны в нулевом порядке по , то и их собственные функции тождественны в нулевом порядке. Предполагая, что спектр собственных значений вырожден, выберем ортогональными друг к другу в нулевом порядке по . Положим

Из соотношений (4.13), (4.15) и (4.16) мы получаем

Умножая равенство (4.17) на и интегрируя, находим

Поскольку — эрмитовый оператор, первый интеграл здесь можно переписать в виде

Далее,

Так как мы удерживаем лишь члейы первого порядка по X, то первый интеграл исчезает. Третий интеграл будет равен

так как ортогональны в нулевом порядке по X. Таким образом, выражение (4.18) принимает вид

Возвращаясь теперь к нашей конкретной задаче, положим

Далее,

где нормированная волновая функция основного состояния водородоподобного атома с зарядом Z; -нормированная водородоподобная волновая функция возбужденного состояния в атоме с зарядом . Знак «плюс» относится к пара-состояниям; знак «минус» — к орто-состояниям.

Чтобы функции были ортогональны, надо предположить ортогональность функций . (Это всегда верно для . При мы рассматриваем две функции, ортогональные в нулевом порядке.) Согласно (4.11) и (4.16), волновые функции нулевого порядка равны

и поправка первого порядка к энергии есть

Пользуясь условием ортогональности функций , мы можем привести это выражение к виду

Интеграл J называется прямым. Он описывает кулоновское взаимодействие между распределениями заряда двух электронов плюс взаимодействие внешнего электрона с единичным положительным зарядом, сконцентрированным в ядре. Интеграл К называется обменным. Он определяет частоту, с которой происходит обмен электронов между квантовыми состояниями.

Действительно, пусть в момент первый электрон находится в основном состоянии, а второй — в возбужденном. Тогда волновая функция при будет

В любой более поздний момент времени

По истечении интервала времени два электрона меняются ролями: первый теперь возбужден, а второй находится в основном состоянии. (Это объяснение предполагает, что в момент мы можем отличить первый электрон от второго, что, конечно, нарушает принцип неразличимости. Следовательно, все это рассуждение не следует принимать слишком серьезно.)

Чтобы вычислить интеграл J, мы запишем его в виде

где

Далее,

где

Тогда получаем

Вспоминая, что находим

Интеграл (4.29) можно оценить [7] для конкретных значений . В частности, для больших получаем

где функция быстро убывает с l.

Чтобы убедиться в этом, воспользуемся квазиклассической аппроксимацией («метод ВКБ» — Вентцеля—Крамерса — Бриллюэна), справедливой при больших n. Положим , тогда

Коэффициент Ф при v представляет кинетическую энергию электрона; он положителен при , где

В этой области собственные функции могут быть представлены в виде

Чтобы вычислить нормировочный множитель, надо рассмотреть в нормировочном интеграле лишь область .

При косинус быстро осциллирует и можно заменить его средним значением . Тогда

Последнее равенство можно получить либо путем интегрирования, либо замечая, что . Таким образом,

Далее, при малых (порядка ) и больших член пренебрежимо мал по сравнению с другими слагаемыми в (4.31). Тогда легко видеть, что как функция (4.33), так и точное решение уравнения (4.31) будут иметь вид

    (4.33 а)

где от зависит только а, а не

Поскольку в интеграл (4.29) дают вклад только значения порядка мы получаем

Функция быстро убывает при больших l, так как в соответствии с (4.28) в J дает вклад только область Электроны с малым орбитальным квантовым числом имеют большую вероятность проникнуть в оболочку чем электроны с большим (вероятность найти электрон в окрестности ядра пропорциональна ). Вводя обозначение мы можем сложить невозмущенную энергию и энергию возмущения J для внешнего электрона в поле ядерного заряда

Это — уровни энергии в форме Ридберга, обычной в спектроскопии;

Чтобы еычислить обменный интеграл К, напишем его в виде

Разлагая по сферическим гармоникам, видим, что вклад дает лишь член с все остальные члены уничтожаются в силу ортогональности сферических гармоник.

Таким образом, получаем

и

Здесь использована симметрия подынтегрального выражения относительно перестановки аргументов

Далее можно воспользоваться теми же качественными соображениями, что и в случае интеграла J. Очевидно,

где быстро падает при больших I. Полагая

можем написать

Положительный знак относится к пара-гелию, отрицательный— к орго-гелию. Член называется поправкой Ридберга. Наши расчеты показывают, что при больших она достигает некоторого предела.

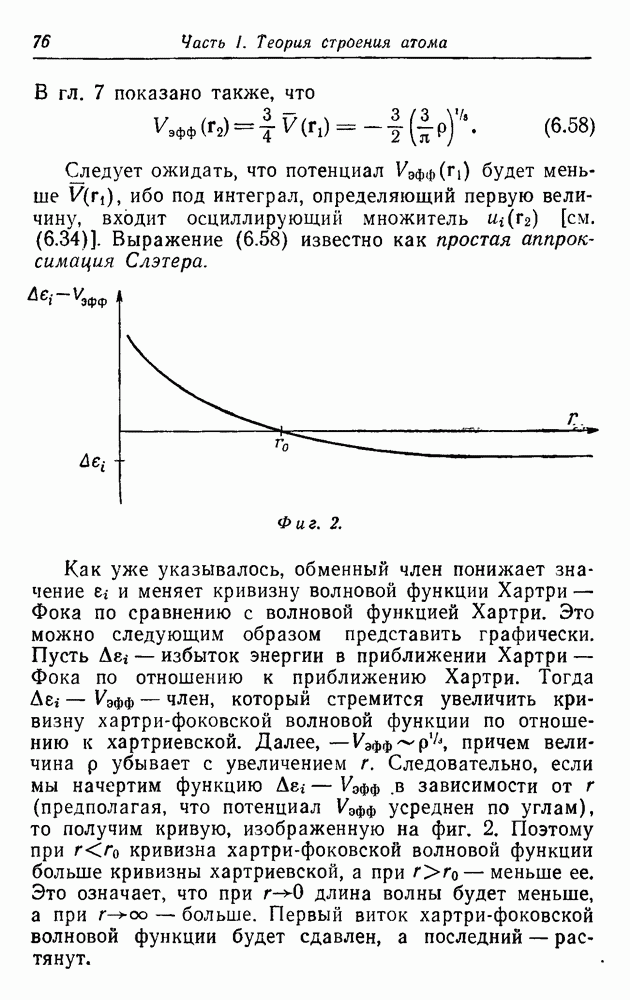
В действительности точные волновые функции Не нельзя представить просто в виде произведения двух независимых одночастичных волновых функций. Наличие одного электрона в некотором определенном положении влияет на волновую функцию другого. Кулоновское отталкивание одного электрона поляризует распределение заряда другого так, чтобы по возможности раздвинуть заряды. Влияние поляризации на кулоновскую и обменную поправки было рассчитано. Поправка к а оказалась весьма малой [7], но поправка к кулоновскому члену заметна. Окончательный результат гласит:

где постоянно при больших и уменьшается с ростом но не так быстро, как с [7].

В табл. 2 приведены наблюдаемые и вычисленные значения поправки Ридберга для гелия. Через обозначены наблюдаемые поправки Ридберга для пара- и орго-гелия соответственно. Столбцы представляют рассчитанные и наблюдаемые усредненные поправки Ридберга, которые и должны совпадать; должны совпадать также цифры в двух последних столбцах таблицы.

Таблица 2. Поправки Ридберга для состояний Не с большим главным квантовым числом

Согласие оказывается хорошим для Р- и -состояний. Для обменной части в -состояниях метод Гейзенберга явно непригоден. (Точное согласие для кулоновской части является случайным.) Если принять во внимание неортогональность функций типа то результат для обменного члена имеет даже неправильный знак. Необходимы поэтому лучшие волновые функции. Такие функции дает метод Фока, детально обсуждаемый ниже. Рассчитанные поправки Ридберга равны тогда соответственно для орто- и парагелия. Экспериментальные значения суть и -0,140.