6. САМОСОГЛАСОВАННОЕ ПОЛЕ

Предварительные интуитивные соображения

Следуя Хартри, предположим, что каждому электрону многоэлектронной системы можно приписать свою индивидуальную волновую функцию. Это означает, что на каждый электрон действует единый эквивалентный потенциал, создаваемый другими электронами и ядрами. Этот потенциал можно вычислить, постулируя, что каждому электрону можно сопоставить плотность заряда, равную заряду электрона , помноженному на плотность вероятности положения электрона в пространстве. Тогда эквивалентный потенциал для электрона будет

Здесь индекс k обозначает набор квантовых чисел, описывающих состояние электрона. Суммирование распространяется на все электроны, кроме

В случае системы из N электронов мы приходим, таким образом, к системе N нелинейных интегродифференциальных уравнений

Следующее приближение состоит в замене потенциала его значением, усредненным по углам векпь . Таким образом, мы получаем сферически симметричный потенциал

Это так называемая аппроксимация центрального поля. (Из дальнейшего будет видно, что это очень хорошая аппроксимация.) Решения уравнения (6.2) после

указанных упрощений можно представить в виде произведений радиальных функций и сферических гармоник

При этом функция удовлетворяет дифференциальному уравнению

целое число определяется из условия, чтобы функция имела узел, не считая узлов в точках Последнее условие приводит к упорядочению собственных значений , а именно увеличивается с увеличением n.

Ясно, что даже со всеми этими предположениями мы не сможем точно решить N уравнений вида (6.2). Процедура Хартри состоит в решении этой системы методом последовательных приближений, учитывающих требование самосогласования. Последнее означает, что потенциал, вычисленный с помощью решения (6.2), должен с достаточной точностью совпасть с начальным потенциалом.

Очевидно, в методе Хартри пренебрегают корреляциями между положениями электронов. Это пренебрежение содержится в допущении существования одночастичных волновых функций, т. е. в представлении полной волновой функции системы в виде произведения одноэлектронных волновых функций. Последнее означает также, что в методе Хартри игнорируются соображения симметрии. Принцип Паули, однако, можно учесть, выбирая подходящим образом квантовые числа одноэлектронных состояний.

Вариационный вывод

Хартри пришел к уравнениям (6.2) и (6.5) путем физически разумных рассуждений интуитивного характера. Покажем сейчас, как можно получить аналогичные результаты из вариационного принципа. При этом мы обобщим результаты Хартри, принимая во внимание

условие симметрии. Это обобщение было дано Фоком и Слэтером и известно как теория Хартри — Фока.

В качестве вариационной пробной функции возьмем детермин а нтную функцию вида

Каждая одночастичная функция, фигурирующая в детерминанте (6.6), представляет собой произведение пространственной и спиновой функций, причем последняя имеет вид либо либо -функции. Все одночастичные функции должны быть ортонормированы

Интегрирование здесь проводится по пространственным и спиновым координатам. Поскольку одночастичные функции с различными спинами автоматически ортогональны, равенство (6.7) сводится к условию ортонормированности пространственных одночастичных функций, соответствующих одинаковым спиновым функциям. Этим обеспечивается нормировка функции и вариационный принцип принимает вид

Матричные элементы между детерминантныма волновыми функциями

Рассмотрим задачу о вычислении матричных элементов произвольного оператора F, действующего на все электроны, между детерминантными волновыми функциями. (Эта задача представляет и общий интерес.) Заметим

метим для этой цели, что функцию (6.6) можно записать в виде

Здесь сумма распространяется на все перестановки, и значок есть либо +1, либо —1 в зависимости от того, является ли четной или нечетной перестановкой чисел

Чтобы вычислить интеграл обозначим одночастичные функции, соответствующие через , а функции, соответствующие через . Тогда

Заметим, что в конечной волновой функции мы переставили электроны, а в начальной волновой функции переставили состояния. Выражение (6.9) можно упростить, замечая, что оператор F должен быть симметричен по координатам всех электронов (в силу тождественности последних).

Чтобы упростить выражение (6.10), удобно сгруппировать вместе члены, относящиеся к одинаковым электронным координатам. Поэтому в произведении по положим это ничего не изменит, так как будет пробегать все значения от 1 до N, когда те же значения пробегает индекс i. Таким образом,

    (6.10 а)

Заметим, что . Но есть лишь «немая» переменная интегрирования, поэтому интеграл (при любых заданных Р и Q) не изменится, если заменить обозначение на i (здесь важна симметрия F по всем электронным координатам). Далее, при заданном Q можно просуммировать по всем перестановкам PQ и перебрать

таким образом все перестановки Р. Тогда

Теперь интеграл (и коэффициент ) совершенно не зависит от Q для каждого данного поэтому полный вклад равен произведению на вклад простейшей (т. е. тождественной) перестановки. Принимая во внимание нормировочный множитель и заменяя опять обозначение PQ на Р, получаем

Рассмотрим теперь частные виды оператора

1. Оператор Вследствие ортогональности одноэлектронных волновых функций если нет такого оператора Р, что для всех i. В силу условий (6.7) может быть не более одного оператора Р. Будем считать (здесь и в дальнейшем), что детерминант упорядочен определенным образом. Именно, пусть тождественные функции v и и расположены в одном и том же порядке. Тогда упомянутая перестановка Р является тождественной и

2. Оператор где — одноэлектронный оператор, действующий на электрон . Если и, более чем для одного , то . Если для какого-то значения , но для всех кроме , то

Если , для всех , то

В выражения (6.13) и (6.14) дает вклад только тождественная перестановка

3. Оператор Суммирование здесь распространяется на все различные пары индексов и величина есть оператор, действующий на электроны I и . Если более чем для двух значений t, то Предположим теперь, что для всех . Тогда

где суммирование идет по всем парам индексов и

Первый член в (6.15) происходит от перестановки второй — от перестановки , т. е. от перемены мест электронов. Это, конечно, нечетйая перестановка, т. е. . Интегрирование в (6.16) идет по пространственным и спиновым координатам, и индексы 1, 2 отмечают «немые» переменные. Если при каком-то значении i выполняется неравенство но при всех кроме мы имеем то

Если для каких-то значений i и справедливы неравенства но при всех k, кроме мы имеем то

Вывод уравнений Хартри — Фока

Возвратимся теперь к частной задаче о вычислении интеграла . Здесь . Следовательно, для всех i. Запишем гамильтониан в виде

, где

Тогда из равенств (6.14) и (6.15) следует

    (6.20а)

Запишем формулу (6.20 б), указывая явно пространственное интегрирование и суммирование по спиновым переменным

[Здесь принято во внимание равенство ] Вспоминая, что

мы получаем

Первый член во второй сумме называется прямым, а второй — обменным. Заметим, что обменный член равен нулю, если спины в двух состояний каждой пары различны. (Это есть еще один пример отсутствия обменных эффектов для тождественных частиц, если их волновые функции не перекрываются; см. стр. 35.)

В соответствии с условиями (6.8) и (6.7) напишем

при дополнительных условиях, налагаемых на одночастичные функции с одинаковым спином,

Чтобы удовлетворить этим условиям, воспользуемся методом неопределенных множителей Лагранжа. Именно, потребуем, чтобы выполнялось равенство

Положим Тогда два члена во второй сумме комплексно сопряжены друг другу.

Выполним теперь вариацию по некоторой функции Поскольку среднее значение стационарно, равенство (6.23 а) должно быть справедливо и по отношению к вариациям любой из функций Пользуясь стандартной вариационной техникой и принимая во внимание свойства эрмитовости и симметрии операторов, приходим к выражению

Складывая это с вариацией членов, остающихся в формуле (6.23 а), приходим к выражению вида

Мы удовлетворим этому равенству, если потребуем, чтобы каждый член в отдельности был тождественно равен нулю. Тогда, поскольку вариации произвольны, подынтегральное выражение также должно равняться нулю. Таким образом, получаем

Это — уравнение Хартри — Фока [3].

Произведем теперь унитарное преобразование функций Очевидно, оно не изменит результатов минимизации, так как такие преобразования оставляют неизменными детерминанты (а, следовательно, и детерминантные волновые функции). Пусть

Далее, чтобы не перепутывать спины, потребуем чтобы если Умножим уравнение (6.24) на и просуммируем его по i; в результате получаем уравнение Хартри — Фока для . Воспользуемся соотношениями [3]

Применяя их к преобразованному уравнению Хартри—Фока, замечаем, что его вид остается неизменным, а коэффициенты преобразуются как матричные элементы. Поскольку матрица эрмитова можем выбрать унитарное преобразование, которое диагонализует ее. Введем обозначения . Тогда преобразованное уравнение Хартри — Фока будет иметь вид (мы опускаем штрих и полагаем

Уравнение Хартри — Фока отличается от уравнения Хартри (6.1) или (6.2) добавочным членом

Второе слагаемое в левой части равенства есть обменный интеграл. Выражение (6.28) возникло потому, что мы пользовались детерминантными пробными функциями [см. (6.15)]. Если бы мы воспользовались пробной волновой функцией в виде произведения одночастичных функций, то член (6.28) не появился бы, и мы получили бы уравнение Хартри. Обсудим теперь физический смысл обменного члена.

Рассмотрение обменного члена

Та часть уравнения Хартри—Фока, которая совпадает с уравнением Хартри, имеет и тот же самый физический смысл: она описывает электрон, движущийся

в эквивалентном иоле, созданном другими электронами и ядрами.

Обменный член, который мы перепишем в виде

есть частный случай нелокального потенциала. [Для удобства мы опустили здесь множитель означает, что последующее суммирование проводится по одночастичным состояниям, соответствующим одному и тому же спину.] Входящий в уравнение Шредингера для член вида

где

называется нелокальным потенциалом. В нашем случае и

Любой локальный потенциал можно рассматривать как нелокальный, полагая

Определим средний потенциал

а также эффективный потенциал

Тогда уравнение Шредингера примет вид

Общие свойства решений уравнения (6.35) следующие. Лапласиан от теперь не обязательно обращается

в нуль при . Следовательно, точки перегиба функции не обязаны совпадать с нулями

Величины вещественны, а решения уравнения (6.35), принадлежащие различным значениям ортогональны. В этом можно убедиться обычным путем. Именно, умножим уравнение для на , а уравнение для на и вычтем одно из другого. Получим

Пользуясь эрмитовостью оператора U и переобозначая немые переменные интегрирования во втором слагаемом в правой части равенства, получаем желаемый результат. Видно также, что наш метод множителей Лагранжа удачен, ибо эти множители как раз и были явно введены для того, чтобы сделать функции ортогональными. Кроме того, величины - оказываются вещественными.

Определим величину называемую матрицей плотности,

Если бы все состояния j были заняты, мы получили бы, в силу условия полноты,

и, следовательно,

Мы покажем, что формула (6.39) остается в силе, даже если не все состояния заняты.

На языке матрицы плотности мы имеем

Таким образом, величину можно интерпретировать как потенциал в точке , созданный плотностью

заряда . Так как , то V есть потенциал в точке , возникающий из-за отсутствия одного электрона. Полная потенциальная энергия электрона в теории Хартри — Фока обусловлена взаимодействием его с ядрами, со всеми электронами с противоположным спином и, наконец, с распределением заряда электронов с тем же спином, что и у данного. Последнее распределение создано зарядом, на единицу меньшим, чем у полного числа электронов в данном спиновом состоянии. Получается так, как если бы рассматриваемый электрон вел за собой дырку. Эта так называемая фермиевская дырка связана с принципом Паули (с антисимметрией волновой функции), благодаря которому электроны с одинаковым спином удерживаются вдалеке друг от друга. В модели Хартри—Фока потенциальная энергия меньше, чем в модели Хартри, так как в первой модели остальные электроны находятся в среднем дальше от рассматриваемого электрона, чем во второй.

Физический смысл собственных значений

Выясним теперь физический смысл величин фигурирующих в уравнениях Хартри — Фока. Умножая уравнение (6.27) на и и интегрируя, получаем

    (6.41 а )

Это есть среднее значение той части энергии, которая зависит от состояния электрона.

Далее, из выражения (6.22) видим, что

    (6.416)

Рассмотрим энергию, необходимую для удаления электрона. Очевидно, она равна разности энергий иона и атома. Допустим, что одночастичные волновые функции для иона и для атома одни и те же. Тогда искомая разность будет равна как раз среднему значению тех членов в гамильтониане, которые зависят от координат удаляемого электрона L Согласно равенству

(6.41 а), это есть не что иное, как . Этот результат известен как теорема Купмена.

Если волновая функция иона, построенная из атомных орбиталей, задается с ошибкой , то энергия иона получается с ошибкой порядка , так как вариационный метод дает стационарные значения энергии. Для многоалектронных атомов значение будет весьма мало. Даже для гелия ошибка в оценке энергии не превосходит 0,1 ридберг.

Следует ясно понимать, что результат, полученный таким путем, отнюдь не дает верхней границы для точной энергии связи. В самом деле, мы взяли здесь разность двух верхних границ. Разумеется, эта разность дает по-прежнему хорошее приближение.

Сферическая симметрия и уравнение Хартри — Фока

Докажем, что для атомов с замкнутыми оболочками самосогласованный потенциал сферически симметричен. Под замкнутой оболочкой понимается случай, когда все состояния, соответствующие заданным значениям , заняты. Докажем высказанное утверждение, допустив, что решение имеет вид . Отсюда будет определен эквивалентный потенциал, который окажется сферически симметричным. Тем самым будет доказано, что наше решение является самосогласованным.

Положим

Пользуясь теоремой сложения для сферических гармоник

получаем

Тогда

где коэффициент 2 появляется из-за суммирования по двум ориентациям спина. Таким образом, кулоновский потенциал сферически симметричен. Далее, имея ввиду обменный член, составим сумму

Здесь нет коэффициента 2, так как в обменном члене суммирование ведется только по электронам с одинаковым спином. Соответственно находим

Рассмотрим сначала интеграл по . Разложим по функциям . Произведения суть полиномы по Следовательно,

их можно разложить по функциям

Эти коэффициенты суть частные случаи более общего выражения

Видно, что они отличны от нуля только при условии

Имеем далее

При интегрировании по в формуле (6.46) отличный от нуля результат дадут лишь члены с

Собирая формулы, приводим интеграл по углам к виду

Итак, угловая зависимость обменного члена такова, что он становится эквивалентным центральносимметричному потенциалу. Подставляя эти результаты в уравнение Хартри—Фока, получаем радиальное волновое

уравнение в виде

    (6.53)

где

Для замкнутых оболочек аппроксимация центрального поля является точной, а не приближенной. Для незамкнутых оболочек она оправдывается, поскольку обыч но есть лишь одна незаполненная оболочка. К тому же в низшем энергетическом состоянии атома электроны в той мере, в какой это разрешается принципом Паули, стремятся занять оболочку со спинами, ориентированными в одном направлении (см. гл. 8). Таким образом, даже наполовину заполненная оболочка приводит к сферически симметричному эквивалентному потенциалу. Самый неблагоприятный случай возникает, когда в оболочке имеется I электронов. Оболочки, встречающиеся в реальных атомах, таковы, что . Если и в этой оболочке есть один электрон, то потенциал, действующий на такой электрон, очевидно, будет сферически симметричным, так как электрон не действует сам на себя (кулоновский и обменный члены взаимно уничтожаются). Для и двух электронов необходимо рассматривать лишь взаимодействие между этими двумя электронами, так что предположение о сферической симметрии по-прежнему должно быть очень хорошим; оно должно быть приемлемым даже при особенно потому, что этот случай встречается лишь при очень больших значениях Z. Таким образом, для атомов аппроксимация центрального поля дает очень хорошее приближение.

(В ядрах дело обстоит иначе, так как значения I там гораздо больше, а ядерные спины имеют тенденцию к антипараллельной ориентации.)

Приближенная трактовка обменного члена

Величину обменного члена в теории Хартри — Фока можно оценить с помощью волновых функций модели Томаса — Ферми. Основные результаты этой модели (которую мы подробно рассмотрим в гл. 7) состоят в следующем. Предполагается, что потенциальная энергия электронов постоянна и, следовательно, волновые функции их суть плоские волны. Считается, что электроны занимают все состояния с импульсами , где — импульс Ферми,

а р — плотность электронов в рассматриваемой точке. Тогда получается

где

и

Чтобы вычислить этот интеграл, надо ввести множитель сходимости переходя в конце концов к пределу при . Тогда в соответствии с формулой (6.39). Средний потенциал

В гл. 7 показано также, что

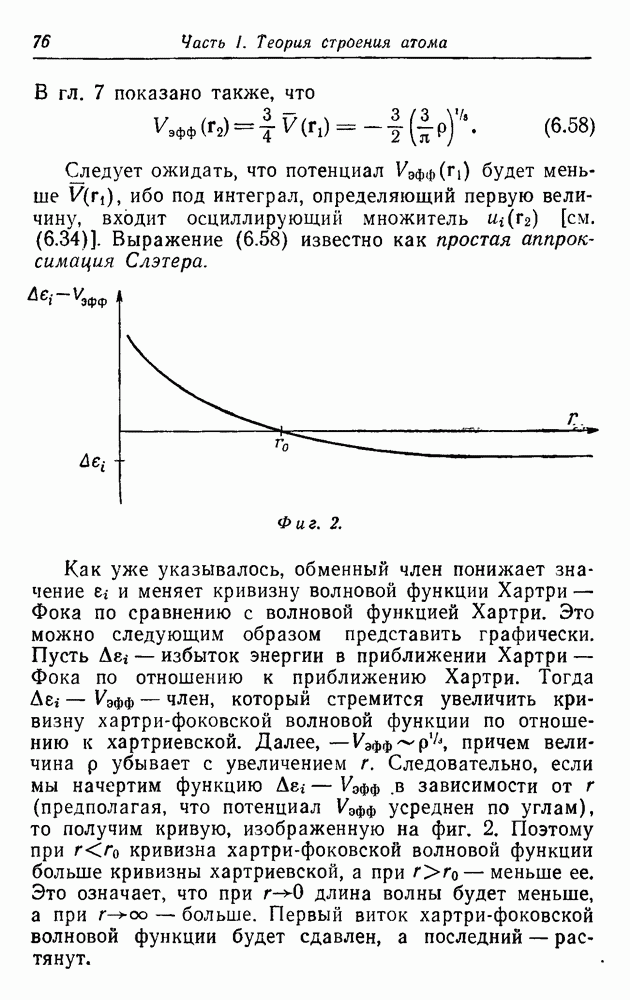
Следует ожидать, что потенциал Уэфф) будет меньше ибо под интеграл, определяющий первую величину, входит осциллирующий множитель [см. (6.34)]. Выражение (6.58) известно как простая аппроксимация Слэтера.

Фиг. 2.

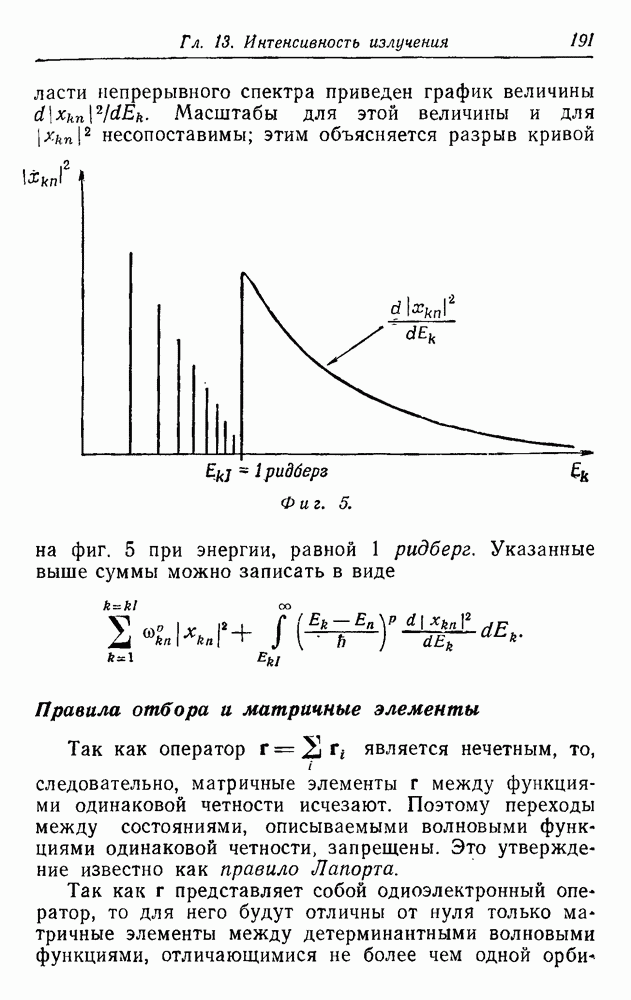
Как уже указывалось, обменный член понижает значение и меняет кривизну волновой функции Хартри — Фока по сравнению с волновой функцией Хартри. Это можно следующим образом представить графически. Пусть — избыток энергии в приближении Хартри — Фока по отношению к приближению Хартри. Тогда — член, который стремится увеличить кривизну хартри-фоковской волновой функции по отношению к хартриевской. Далее, причем величина убывает с увеличением . Следовательно, если мы начертим функцию в зависимости от (предполагая, что потенциал усреднен по углам), то получим кривую, изображенную на фиг. 2. Поэтому при кривизна хартри-фоковской волновой функции больше кривизны хартриевской, а при — меньше ее. Это означает, что при длина волны будет меньше, а при — больше. Первый виток хартри-фоковской волновой функции будет сдавлен, а последний — растянут.

Результаты вычислений

Рассмотрим выражение для обменного потенциала, фигурирующего в уравнении (6.53)

Очевидно, оно максимально при Это легко понять, так как

Далее, Следовательно, наибольший вклад дают члены с

Полный заряд внутри сферы радиуса в модели Хартри дается выражением

где - полная плотность заряда электронов. Таким образом, есть убывающая функция . Для , близких к нулю, . Поэтому при малых значениях электроны могут подходить к ядру ближе, чем при больших — они «видят» больший эффективный заряд. Следовательно, энергия связи, которая в основном определяется средним значением величины падает с ростом I.

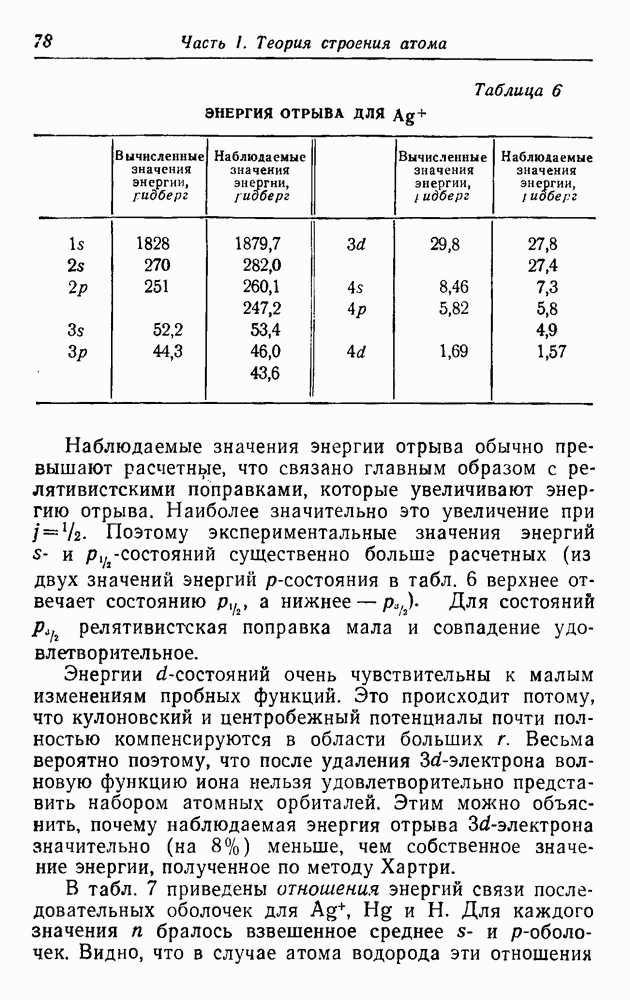
В табл. 6 результаты расчета энергий электронных состояний по методу Хартри — Фока сравниваются с экспериментальными значениями. Последние найдены по положению соответствующих границ поглощения рентгеновского спектра. Как правило, даются два значения энергии, отвечающие . Энергия, необходимая для вырывания электрона из состояния есть ионизационный потенциал . Другие вычисления можно найти в работах [61—63].

Таблица 6. ЭНЕРГИЯ ОТРЫВА ДЛЯ

Наблюдаемые значения энергии отрыва обычно превышают расчетные, что связано главным образом с релятивистскими поправками, которые увеличивают энергию отрыва. Наиболее значительно это увеличение при Поэтому экспериментальные значения энергий s- и -состояний существенно больше расчетных (из двух значений энергий -состояния в табл. 6 верхнее отвечает состоянию а нижнее — ). Для состояний релятивистская поправка мала и совпадение удовлетворительное.

Энергии -состояний очень чувствительны к малым изменениям пробных функций. Это происходит потому, что кулоновский и центробежный потенциалы почти полностью компенсируются в области больших . Весьма вероятно поэтому, что после удаления -электрона волновую функцию иона нельзя удовлетворительно представить набором атомных орбиталей. Этим можно объяснить, почему наблюдаемая энергия отрыва -электрона значительно (на 8%) меньше, чем собственное значение энергии, полученное по методу Хартри.

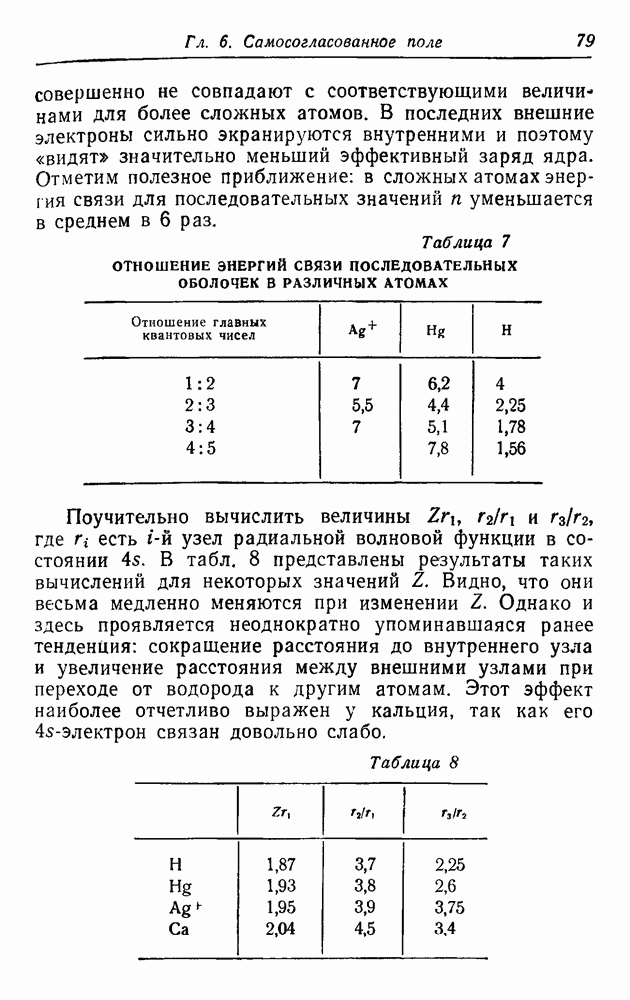
В табл. 7 приведены отношения энергий связи последовательных оболочек для и Н. Для каждого значения бралось взвешенное среднее s- и -оболочек. Видно, что в случае атома водорода эти отношения

совершенно не совпадают с соответствующими величинами для более сложных атомов. В последних внешние электроны сильно экранируются внутренними и поэтому «видят» значительно меньший эффективный заряд ядра. Отметим полезное приближение: в сложных атомах энергия связи для последовательных значений уменьшается в среднем в 6 раз.

Таблица 7. ОТНОШЕНИЕ ЭНЕРГИЙ СВЯЗИ ПОСЛЕДОВАТЕЛЬНЫХ ОБОЛОЧЕК В РАЗЛИЧНЫХ АТОМАХ

Поучительно вычислить величины , где есть узел радиальной волновой функции в состоянии . В табл. 8 представлены результаты таких вычислений для некоторых значений Z. Видно, что они весьма медленно меняются при изменении Z. Однако и здесь проявляется неоднократно упоминавшаяся ранее тенденция: сокращение расстояния до внутреннего узла и увеличение расстояния между внешними узлами при переходе от водорода к другим атомам. Этот эффект наиболее отчетливо выражен у кальция, так как его -электрон связан довольно слабо.

Таблица 8

Хартри определяет константу экранирования из выражения

где — радиус соответствующей водородной орбиты, а функция нормирована. В табл. 9 представлены значения для различных Z. Видно, что действительно несколько больше, чем Хартри показал, что величина рассматриваемая как функция аргумента лишь слабо зависит от Z, и эту зависимость легко аппроксимировать простой интерполяцией.

Таблица 9. КОНСТАНТА ЭКРАНИРОВАНИЯ ДЛЯ РАЗЛИЧНЫХ Z

Слэтер [14] дал ряд полезных, общих, но не совсем строгих правил вычисления константы экранирования. Для состояний с он получает . В той же статье можно найти и правила применения этих констант.

Большие значения n

При больших , т. е. для состояний, получаемых оптическим возбуждением, вычисления облегчаются благодаря следующим двум упрощениям. Во-первых, вероятность обнаружить вблизи ядра электрон, находящийся в сильно возбужденном состоянии, мала. Поэтому волновая функция совокупности невозбужденных электронов атома с хорошей точностью аппроксимирует волновой функцией соответствующего иона. Во-вторых, при , большем некоторого радиуса R, оптические электроны движутся в поле с эквивалентным потенциалом вида Поэтому при мы имеем водородную

волновую функцию со сдвинутой фазой. Фазовый сдвиг есть медленно меняющаяся функция энергии. Зависимость от энергии слаба из-за того, что значения мало отличаются друг от друга для различных и все они гораздо меньше потенциальной энергии.

В квазиклассическом приближении волновая функция имеет вид , где обычно появляющийся здесь квадратный корень из импульса и а — некоторая функция от . Именно, равна , где — фаза волновой функции атома водорода, отвечающая той же самой энергии. Согласно известным формулам квазиклассического метода для внешней точки поворота мы имеем , где есть число узлов функции и следовательно, . С другой стороны, фазу можно получить как функцию энергии вычислив фазовый интеграл в форме (4.33). Введем в рассмотрение число , положив Тогда

и

где (так называемая поправка Ридберга) не зависит от . Формула (6.62) есть первоначальная формула Ридберга.

Периодическая система

Принцип Паули вместе с вычислениями по методу Хартри—Фока дает нам возможность объяснить периодическую систему элементов. Именно, электронные оболочки заполняются в порядке возрастания энергии, а принцип Паули ограничивает число электронов в каждой данной оболочке.

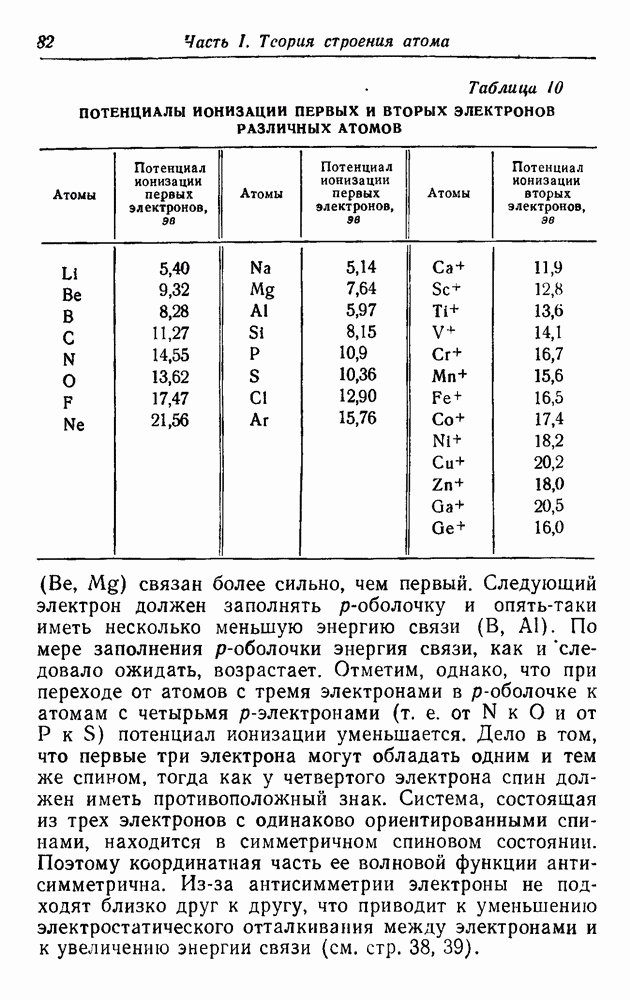
В табл. 10 приведены потенциалы ионизации для первых (2-й и 4-й столбцы) и вторых (6-й столбец) электронов различных атомов. Видно, что щелочные металлы и соответствующие ионы типа имеющие по одному электрону вне заполненных оболочек, обладают наименьшей энергией связи. Второй -электрон

Таблица 10. ПОТЕНЦИАЛЫ ИОНИЗАЦИИ ПЕРВЫХ И ВТОРЫХ ЭЛЕКТРОНОВ РАЗЛИЧНЫХ АТОМОВ

связан более сильно, чем первый. Следующий электрон должен заполнять -оболочку и опять-таки иметь несколько меньшую энергию связи . По мере заполнения -оболочки энергия связи, как и следовало ожидать, возрастает. Отметим, однако, что при переходе от атомов с тремя электронами в -оболочке к атомам с четырьмя -электронами (т. е. от N к О и от Р к S) потенциал ионизации уменьшается. Дело в том, что первые три электрона могут обладать одним и тем же спином, тогда как у четвертого электрона спин должен иметь противоположный знак. Система, состоящая из трех электронов с одинаково ориентированными спинами, находится в симметричном спиновом состоянии. Поэтому координатная часть ее волновой функции антисимметрична. Из-за антисимметрии электроны не подходят близко друг к другу, что приводит к уменьшению электростатического отталкивания между электронами и к увеличению энергии связи (см. стр. 38, 39).

В 6-м столбце выписаны потенциалы ионизации ионов, у которых внешней является оболочка Мы взяли ионы, а не нейтральные атомы, поскольку для последних имеет место конкуренция между и -оболочками. Энергия связи возрастает до тех пор, пока в оболочке не окажется пять электронов, после чего по тем же причинам, о которых говорилось выше, происходит некоторое уменьшение потенциала ионизации Заполнение оболочки заканчивается на Начиная с происходит заполнение оболочки что обнаруживается в уменьшении энергии связи. Аналогично первый связан слабее, нежели второй

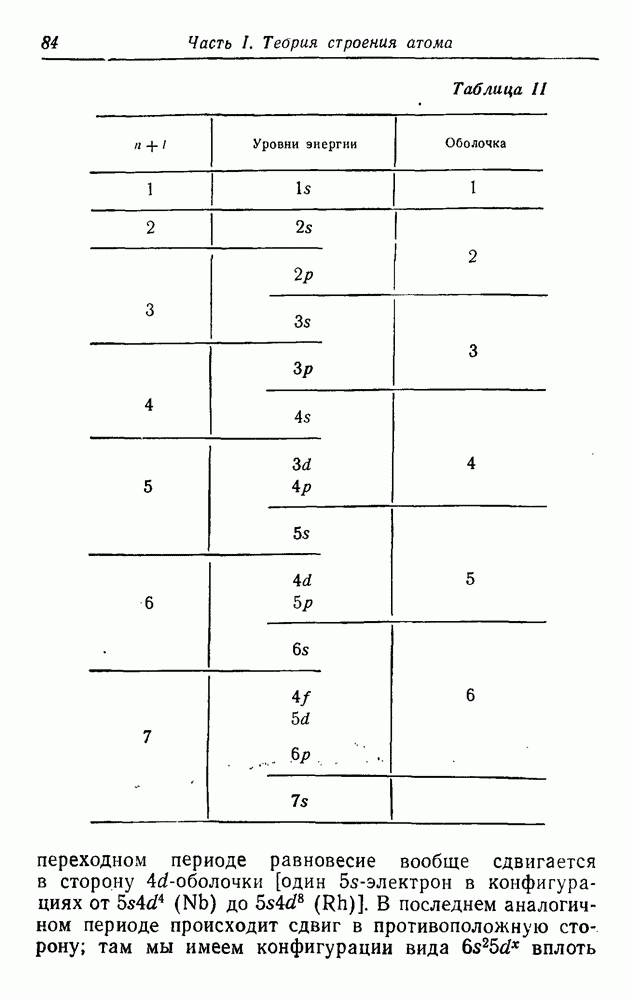
Как уже говорилось, порядок заполнения всех оболочек определяется принципом Паули и условием минимальности энергии возникающих электронных состояний. Маделунг сформулировал следующее простое эвристическое правило заполнения уровней нейтральных атомои. Заполнение идет в порядке возрастания суммы Для каждого значения заполнение идет в порядке возрастания n. Заполнение каждой оболочки заканчивается на -электронах, исключая первую оболочку, которая завершается заполнением состояний . В табл. 11 представлен порядок заполнения уровней согласно этому правилу.

Во всех случаях -оболочки очень чувствительны и конкурируют с -оболочками, имеющими то же - самое значение Таблица, приведенная в книге [1], позволяет наглядно увидеть эту конкуренцию. Сначала два электрона заполняют оболочку Следующие три электрона попадают в оболочку Затем у вместо одного из электронов появляется дополнительный электрон в оболочке что дает конфигурацию Это снова указывает на значительную стабильность наполовину заполненной оболочки. У Mn опять видим конфигурацию наряду со стабильной конфигурация сохраняется вплоть до никеля. Далее, дополнительная стабильность -оболочки снова приводит к тому, что в состоянии остается один электрон. Поэтому медь часто проявляет свойства как одновалентного, так и двухвалентного элемента. В следующем

Таблица 11 (см. скан)

переходном периоде равновесие вообще сдвигается в сторону -оболочки [один -электрон в конфигурациях от до ]. В последнем аналогичном периоде происходит сдвиг в противоположную сторону; там мы имеем конфигурации вида вплоть

. Изменение схемы заполнения при переходе от к -оболочке происходит, вероятно, благодаря возрастанию заряда ядра, а в случае перехода от к -оболочке — из-за вмешательства -оболочки, которая эффективно экранирует -электроны.

Следует напомнить, что в силу антисимметрии волновых функций атомов нельзя приписать каждому электрону в отдельности определенный набор квантовых чисел. Высказывания типа «электрон в состоянии следует понимать только в том смысле, что слэтеровский детерминант содержит состояние с квантовыми числами .