8. ТЕОРИЯ МУЛЬТИПЛЕТОВ. СЛОЖЕНИЕ МОМЕНТОВ

Приближение центрального поля, использованное нами в гл. 6 и 7, приводит к тому, что атом с незаполненной оболочкой представляет собой систему с высоким вырождением по энергии. Для оболочки имеются электронных состояний с одинаковой энергией. Если оболочку заполняют электронов, то существует способов, которыми эти электроны можно разместить по оболочке. Следовательно, кратность вырождения равна Фосфор, например, содержащий 15 электронов, имеет электронную конфигурацию Кратность вырождения в этом случае равна 20. Вырождение отсутствует только для заполненных оболочек, для которых .

Вырождение частично снимается, если принять во внимание электростатическое взаимодействие между электронами, энергия которого составляет

Мы будем рассматривать это взаимодействие (за вычетом подходящего» среднего от него) как возмущение. В качестве нулевого приближения возьмем детерминантные волновые функции Хартри—Фока. Соответственно надо найти такие их линейные комбинации, чтобы субматрица гамильтониана размерности была диагональна. Чтобы облегчить задачу, рассмотрим векторы полного орбитального и спинового моментов количества движения для всех электронов в атоме. Каждая декартова компонента этих двух векторов представляет собой, как мы покажем, интеграл движения.

Момент количества движения

Рассмотрим коммутатор [Н, L], где гамильтониан Н дается формулой (1.4), а оператор полного момента L — формулой (2.8). Для простоты рассмотрим двухэлектронную систему. Очевидно, L коммутирует с так как с ними коммутирует . Но поскольку оператор L, пропорционален оператору вращения в пространстве он не может коммутировать с . Тем не менее мы покажем, что . Рассмотрим равенство

где f — произвольная дифференцируемая функция. Имеем

Из соображений симметрии следует, что

Объединяя равенства (8.2) и (8.3), получаем

Последнее соотношение должно быть выполнено для всех компонент. L, т. е.

Выбирая , заключаем, что

Этот вывод с очевидностью обобщается и на число электронов, большее двух, откуда следует, что

Тот же результат может быть получен с помощью общей теоремы о коммутаторах. Пусть А — эрмитовский линейный оператор, полный набор собственных значений которого А и собственных функций задан равенством . Функция f оператора А определяется следующим образом: есть оператор, удовлетворяющий соотношению

Очевидно, равенство (8.8) выполнено для любой функции, допускающей разложение Лорана. Для всех прочих функций равенство (8.8) служит определением. Конечно, мы должны потребовать, чтобы функция f была определена для всех значений А. Предположим, что , тогда для всех функций определенных соответственно для всех собственных значений А и В. Действительно, поскольку А и В коммутируют, они могут быть одновременно выражены диагональными матрицами. Матрицы операторов в соответствующем представлении также диагональны, их элементы равны соответственно , откуда ясно, что эти матрицы коммутируют. (Более строгое доказательство см. в работе [59].)

Чтобы установить равенство (8.7), заметим прежде всего, что непосредственное дифференцирование дает Отсюда с помощью доказанной теоремы немедленно получается (8.6) и, следовательно, (8.7).

Полный спиновый момент также является интегралом движения. Это утверждение иногда ошибочно «доказывают», ссылаясь на то, что гамильтониан от спина не зависит. Это неверно, так как условие антисимметрии волновых функций связывает выбор спиновых функций с симметрией пространственной волновой функции и, следовательно, с электростатической энергией взаимодействия (см. стр 39 и 82). Подобными рассуждениями можно было бы, например, «доказать», что спины отдельных электронов S также суть интегралы движения, что неверно. Чтобы убедиться в этом, рассмотрим атом, содержащий два электрона, и составим величину , где - собственная функция,

описывающая состояние орто-гелия и соответствующая собственному значению Е. Мы имеем

Но функция несимметрична относительно двух электронов. Значит, ее нельзя представить в виде разложения по антисимметричным собственным функциям, которые только и являются допустимыми. Ее, конечно, нельзя разложить по антисимметричным собственным функциям, принадлежащим энергии Е, что, безусловно, было бы возможно, если бы компонента спина была интегралом движения.

Доказательство того, что полный спиновый момент S коммутирует с гамильтонианом , проводится следующим образом. Рассмотрим, как действует коммутатор на произвольную функцию . Поскольку рассматриваемая функция f может быть разложена по собственным функциям гамильтониана , достаточно выяснить действие на где

причем есть функция пространственных и спиновых координат с должной симметрией. Мы имеем

Оператор проекции полного спина S симметричен относительно всех электронов. Поэтому выражение сохраняет должную симметрию и является допустимой волновой функцией в отличие от функции рассмотренной выше. Поскольку не действует на пространственные координаты, в войдут те же пространственные функции, что и в Мы можем записать

где — все возможные спиновые функции для N электронов; — некоторые пространственные функции. Тогда наше утверждение состоит в том, что

где - другая спиновая функция, a та же пространственная функция, что и прежде. Поскольку гамильтониан Н действует только на пространственные координаты, каждая из пространственных функций должна удовлетворять уравнению (8.10). Но тогда функция 54 также должна удовлетворять уравнению (8.10) с тем же собственным значением Е и, согласно . Это справедливо для всех компонент S, и потому

Поскольку все операторы коммутируют друг с другом, мы можем найти представление, в котором все они диагональны. В этом представлении матричные элементы гамильтониана Н между состояниями, задаваемыми квантовыми числами равны, согласно (2.1),

Это означает, что матрица гамильтониана Н распадается на субматрицы, связывающие только состояния с одинаковыми значениями так как все эти операторы суть интегралы движения.

Сложение моментов

Теперь мы должны построить собственные функции операторов Будем составлять их из произведений одночастичных собственных функций операторов Пусть, например, мы имеем две частицы, не обладающие спином, с моментами количества движения, равными соответственно и -компонентами моментов (мы опускаем множитель А). Произведение является собственной функцией оператора принадлежащей собственному значению . Оператор при этом, вообще говоря, не диагонален. Однако из мультипликативных собственных функций, принадлежащих собственному значению , можно составить и такие линейные комбинации, в которых матрица

диагонализуется. Чтобы это проиллюстрировать, в первых трех столбцах табл. 13 выписаны значения для нескольких значений.

Таблица 13. СЛОЖЕНИЕ МОМЕНТОВ КОЛИЧЕСТВА ДВИЖЕНИЯ

Мы приходим к следующим выводам. Поскольку при существует только одна возможная комбинация, она и должна быть собственной функцией оператора при этом собственное значение последнего должно быть равно где . Далее, наличие двух различных состояний с приводит к секулярному уравнению для диагонализации матрицы собственные значения ее при этом, конечно, равны , где L равно или . Аналогичным образом, для одна линейная комбинация мультипликативных волновых функций дает другая и третья столбце табл. 13 выписаны значения L, которые получаются для линейных комбинаций. Если считать то табл. 13 можно продолжить до . Для этого значения ML величина будет принимать все значения от до при этом . Это приводит к секулярному уравнению порядка ему соответствуют все значения L от до . Далее должен был бы следовать случай, когда

где

Поскольку других значений уже нет, и мы опять приходим к секулярному уравнению порядка . Новых значений L при этом уже не получится. Это значит, что все линейные комбинации функций, указанных в формуле (8.16), необходимы для определения уже известных нам значений L. Дальнейшее уменьшение ML до величины уже не приводит к новым значениям L. Таким образом, возможные значения L равны

где знак модуля предусматривает возможность неравенства Равенство (8.17) есть результат векторного сложения моментов, известный из старой квантовой теории.

Чтобы сложить три момента, сложим сначала два из них, а затем добавим третий к их сумме. Спиновый момент ведет себя совершенно аналогично, и, следовательно, таким же способом можно складывать спиновый момент с орбитальным.

Коэффициенты Клебша — Гордана

Построим теперь формальную теорию сложения моментов и укажем метод определения собственных значений операторов . Запишем собственную функцию в виде разложения

Это есть не что иное, как преобразование, связывающее собственные векторы операторов с собственными векторами операторов . Суммирование производится только по индексам , так как предполагается, что значения и h фиксированы. Задача о сложении моментов сводится к определению элементов матрицы перехода, называемых коэффициентами

Клебша—Гордана (их называют также коэффициентами векторного сложения или коэффициентами Вигнера). Задача существенно упрощается, если применить к обеим частям равенства (8.18) оператор проекции полного момента и вспомнить, что

Тогда

Отсюда следует, что коэффициенты отличны от нуля только при и суммирование в формуле (8.18) фактически производится либо по либо по

Существуют три метода вычисления коэффициентов Клебша—Гордана (если не считать возможности взять их из таблиц). Первый — это метод последовательного спуска. Начнем с . В этом случае, как мы знаем, сумма содержит только один член

Подействовав на функцию (8.20) оператором , мы получим

Отсюда

или

Есть еще одна собственная функция, принадлежащая собственному значению она соответствует

. Поскольку она должна быть ортогональна к функции (8.21), мы имеем

Теперь можно подействовать на обе части равенств (8.21) и (8.22) понижающими операторами и получить новые линейные комбинации для и т. д.

Второй метод принадлежит Рака, который получил замкнутую формулу

где

Здесь z пробегает все целочисленные значения до тех пор, пока аргументы всех факториалов остаются неотрицательными. (Мы ввели здесь новые обозначения:

В частном случае формулы (8.23) и (8.24) принимают вид

Третий метод вычисления коэффициентов Клебша—Горлана — это метод проекционного оператора. Определим проекционный оператор равенством

Произведение содержит здесь все значения (которые могут получиться от сложения L и 5), кроме того, для которого мы ищем коэффициент. Равенство (8.18) можно обратить, полагая

Ограничение как и прежде, приводит к тому, что суммирование фактически производится только по одному индексу J. Действуя на обе части равенства (8.27) проекционным оператором мы обратим в нуль все члены ряда, кроме . Таким образом, получаем

Вследствие унитарности преобразования

Подставляя соотношения (8.18) и (8.29) в формулу (8.28), находим

Таким образом, действуя проекционным оператором на функцию мы получаем ряд, среди членов которого содержится и . Разделив этот ряд на квадратный корень из коэффициента при мы немедленно получим разложение для с должными коэффициентами Клебша — Гордана.

Полезную рекуррентную формулу можно получить, действуя на равенство (8.18) оператором или :

Ясно, что в коэффициенты Клебша—Гордана входит произвольный (одинаковый для них всех) фазовый множитель. Принято считать коэффициент вещественным и положительным. Тогда и все коэффициенты должны быть вещественными.

Поскольку преобразование (8.18) унитарно, выполняются обычные соотношения ортогональности

Заметим, что числа собственных функций в -представлениях должны быть одинаковы. Действительно, в -представлении существует возможных значений ML и возможных значений что дает собственных функций. В -представлении имеется состояний для каждой величины J, принимающей все значения от до Следовательно, полное число состояний составляет

Частные случаи

Рассмотрим теперь несколько частных случаев. Вычислим прежде всего полный момент количества движения для фермионов со спином . При этом величина может быть равна либо либо

и справедливы формулы

Докажем равенство (8.33) по индукции. Заметим, что оно выполняется при Затем подействуем на обе части равенства (8.33) оператором и поделим результат на . При этом получается равенство того же вида, что и (8.33), но с вместо М. Чтобы доказать равенство (8.34), достаточно заметить, что функции ортонормированы. Поскольку пространство этих функций двумерно, равенство (8.34) должно быть справедливо.

Рассмотрим далее сложение двух моментов, одинаковых по величине: . Тогда величина может быть равна . Волновая функция, принадлежащая максимальному значению (это соответствует ), должна даваться формулой

(Мы сокращенно записываем как .) Очевидно, равенство (8.35) симметрично относительно двух моментов. В частном случае двух эквивалентных электронов волновая функция будет симметрична относительно их пространственных координат. Поскольку — симметричный оператор функция также оказывается симметричной. Следовательно, все собственные функции с симметричны относительно двух моментов. При имеются две возможности: или . Из соответствующих собственных функций мы образуем линейные комбинации, приводящие к

и . Единственная нормированная симметричная функция, которую можно таким путем построить, имеет вид

Она должна соответствовать значению . Функция

нормированная и ортогональная к выражению (8.36), соответствует значению помощью прежнего рассуждения мы заключаем, что все собственные функции с антисимметричны.

Для меньших значений М рассуждение протекает аналогично. Если , где — целое число, то возможны следующие пары :

Для случаев, когда , мы можем образовать симметричную и антисимметричную комбинации собственных функций

тогда как при можно образовать только симметричную функцию . Следовательно, имеются симметричных и антисимметричных собственных функций. С другой стороны, если то должно быть симметричных и антисимметричных собственных функций, так как нет состояния, для которого . Действуя понижающим оператором на антисимметричные функции при мы получаем линейно независимых антисимметричных функций, соответствующих . Это исчерпывает все возможные антисимметричные собственные функции. Производя ту же операцию с симметричными функциями, мы получаем симметричных линейных комбинаций типа (8.39). Однако мы знаем, что при фактически

существуют симметричных функций, так что одна из них при этом упущена. Эта функция должна принадлежать значению откуда следует, что собственная функция, принадлежащая должна быть симметрична. И наоборот, при переходе от добавляется одна антисимметричная собственная функция, откуда следует, что собственная функция, принадлежащая антисимметрична. Все состояния с (или 1, если L — полуцелое) характеризуются собственными функциями, симметричными по L и S, все состоя собственными функциями.

Это правило можно использовать, например, при вычислении изотопических спинов двух -мезонов. Изотопический спин одного -мезона равен единице. Следовательно, собственные функции, соответствующие значениям полного изотопического спина и 0, симметричны относительно изотопических спиновых координат двух -мезонов, а собственная функция с антисимметрична.

Сложение моментов для эквивалентных электронов

Рассмотрим задачу о вычислении возможных значений суммарного момента количества движения для нескольких эквивалентных электронов (т. е. электронов в состояниях с одинаковыми числами ). При этом необходим учет принципа Паули, ограничивающего число допустимых комбинаций. В табл. 14 показано, как складываются орбитальный и спиновый моменты для двух эквивалентных электронов. Орбитальные моменты составляют . Их компоненты выписаны в столбцах. Спин каждого электрона равен . Компоненты спина выписаны во столбцах; знак означает , знак означает Значения выписаны в столбцах. В 7-м и 8-м столбцах приводятся возможные значения полного орбитального и спинового моментов, которые могут быть получены для линейных комбинаций собственных функций с данными

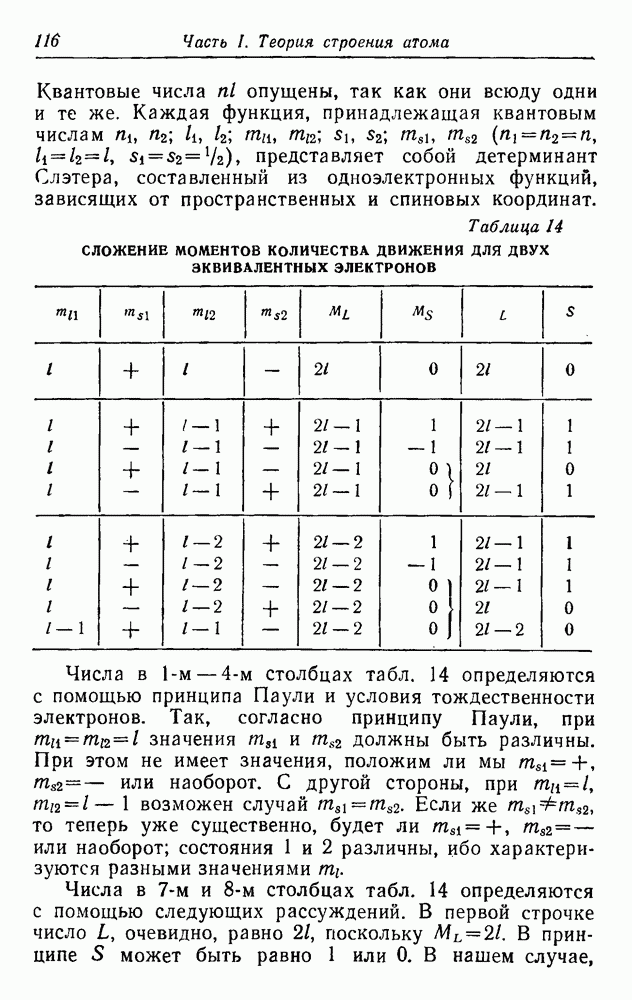
Квантовые числа опущены, так как они всюду одни и те же. Каждая функция, принадлежащая квантовым числам представляет собой детерминант Слэтера, составленный из одноэлектронных функций, зависящих от пространственных и спиновых координат.

Таблица 14. СЛОЖЕНИЕ МОМЕНТОВ КОЛИЧЕСТВА ДВИЖЕНИЯ ДЛЯ ДВУХ ЭКВИВАЛЕНТНЫХ ЭЛЕКТРОНОВ

Числа в 1-м - 4-м столбцах табл. 14 определяются с помощью принципа Паули и условия тождественности электронов. Так, согласно принципу Паули, при значения должны быть различны. При этом не имеет значения, положим ли мы или наоборот. С другой стороны, при возможен случай . Если же , то теперь уже существенно, будет ли — или наоборот; состояния 1 и 2 различны, ибо характеризуются разными значениями т.

Числа в 7-м и 8-м столбцах табл. 14 определяются с помощью следующих рассуждений. В первой строчке число L, очевидно, равно 21, поскольку . В принципе S может быть равно 1 или 0. В нашем случае,

однако, S не может быть равно тогда понижающий оператор производил бы три разрешенных состояния: а мы можем получить только одно. Следовательно, . В следующем ряду имеются четыре возможности с и различными значениями . Первая и вторая строчки соответствуют значению так как Поскольку можно составлять только линейные комбинации собственных функций с данными значениями из этих двух функций никаких линейных комбинаций образовать нельзя. Следовательно, каждая из них в отдельности есть собственная функция операторов L и S с соответствующими собственными значениями.

Состояния в следующих двух строчках имеют одинаковые значения и линейные комбинации соответствующих собственных функций допустимы. Одна линейная комбинация соответствует другая — . Следующий ряд, для которого содержит пять собственных функций. Некоторые линейные комбинации их должны соответствовать значениям Непосредственно видно, что в первых двух строчках стоят собственные функции операторов L и S с указанными там же собственными значениями. Из остальных трех собственных функций можно составлять линейные комбинации, поскольку они принадлежат одинаковым значениям ML и . Одна из линейных комбинаций соответствует другая . Третья функция должна принадлежать значению L, отличному от предыдущих; очевидно, оно равно . Поскольку имеется только одно такое состояние, S = 0.

Значения L и S определялись выше путем перечисления состояний с данными значениями . Другой метод основан на соображениях симметрии. Полная волновая функция должна быть антисимметрична относительно перестановки электронов. Следовательно, в волновая функция есть детерминант Слэтера

Здесь радиальная волновая функция электрона; -сферическая гармоника, — спиновая функция электрона.

В -представлении волновая функция представляет собой линейную комбинацию членов вида (8.40), в которых . Мы видим, что произведение радиальных функций входит общим множителем во все члены функции Поскольку оно симметрично, остальная часть волновой функции, зависящая от углов и спинов, должна быть антисимметричной. Если она представляет собой произведение двух множителей, один из которых зависит только от углов, а другой — только от спинов, то эти множители должны иметь противоположную симметрию по отношению к перестановке электронов. Такая факторизация происходит при так как при этом соответственно выполнены равенства или и произведения или можно вынести как общие множители. При возможно как равенства так и . В этом случае часть волновой функции зависящую от углов и спинов, можно записать в виде

Здесь представляют собой суммы произведений сферических гармоник. Поскольку выражение (8.41) есть собственная функция операторов , каждая из функций также должна быть их собственной функцией. Выше было показано, однако, что для пространственные собственные функции, а следовательно, и функции должны быть симметричны или антисимметричны в зависимости от величины L. Функция (8.41) антисимметрична, следовательно,

откуда

Поэтому выражение (8.41) всегда можно записать в виде

Итак, для двух эквивалентных электронов волновая функция всегда разбивается на произведение радиальной, угловой и спиновой частей, причем угловая и спиновая части обладают противоположной симметрией относительно перестановки электронов. Это означает, что при четном L и при нечетном L. Заметим, что в табл. 14 это правило выполняется. Действительно, пользуясь им, можно получить все значения, входящие в табл. 14.

Для трех и большего числа электронов дать какие-либо общие правила гораздо труднее. Табл. 15 демонстрирует сложение моментов для трех эквивалентных -электронов. Здесь имеются 20 разрешенных состояний (см. стр. 102). Однако таблицу можно сократить, ибо

Таблица 15. СЛОЖЕНИЕ МОМЕНТОВ ДЛЯ ТРЕХ ЭКВИВАЛЕНТНЫХ p-ЭЛЕКТРОНОВ

каждому состоянию с положительным значением можно поставить в соответствие состояние с следует лишь изменить знаки у всех Подобным образом можно независимо изменять знаки у всех Следовательно, достаточно выписать только функции с положительным или равным нулю и положительным Их всего 7, а не 20.

Возможные значения чисел L и S по-прежнему можно найти, перечисляя дозволенные состояния. Соображения симметрии здесь неприменимы, поскольку мы уже не складываем два одинаковых момента. Фигурные скобки указывают, что необходимо брать линейные комбинации. Видно, что получается одно одно и одно -состояния. Первое из них имеет магнитных подсостояния второе — а третье — магнитных подсостояний. Как и следовало ожидать, полное их число равно 20. Это важная проверка полноты нашей таблицы состояний.

Во всех до сих пор рассмотренных случаях имелось не более одного состояния для каждой комбинации чисел LS. В следующей главе мы увидим, что это существенно упрощает вычисление энергетических уровней. Простейшей конфигурацией, содержащей только эквивалентные электроны, для которой это уже несправедливо, является (три эквивалентных -электрона). В этом случае имеются два -состояния. Они различаются только энергией, и вычислить их энергию труднее, чем в случае, когда имеется только одно состояние с данным набором . Конфигурации соответствуют пять пар состояний с одним и тем же набором ; для -оболочки наличие нескольких состояний с одним и тем же набором становится общим правилом [3].