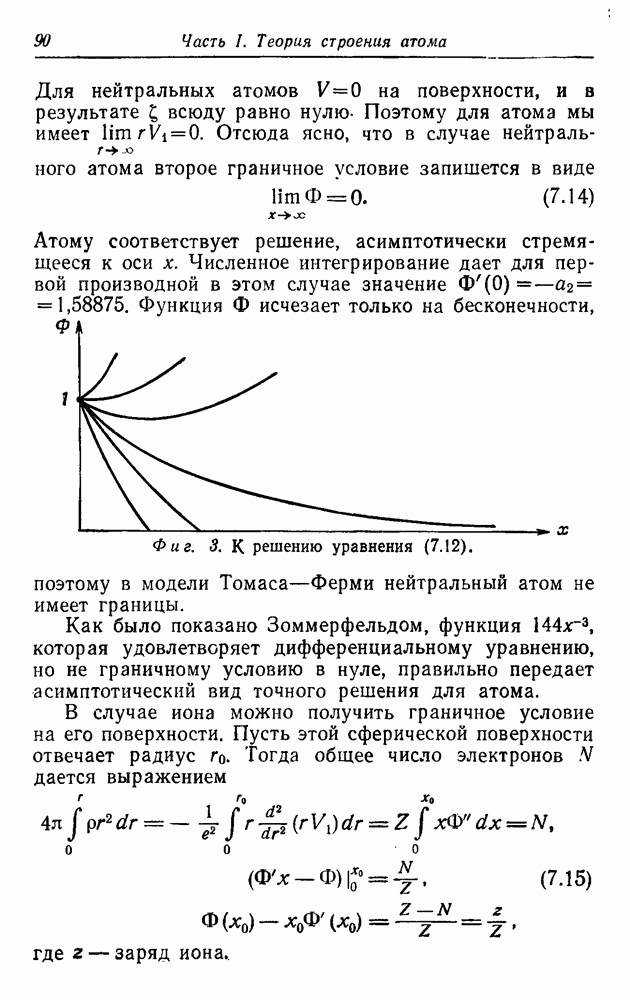
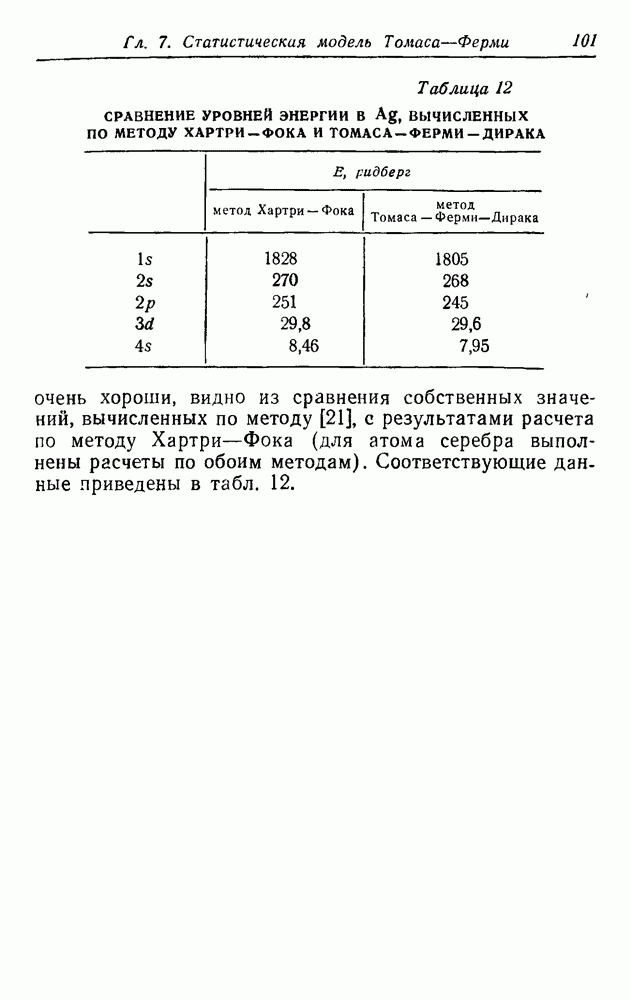
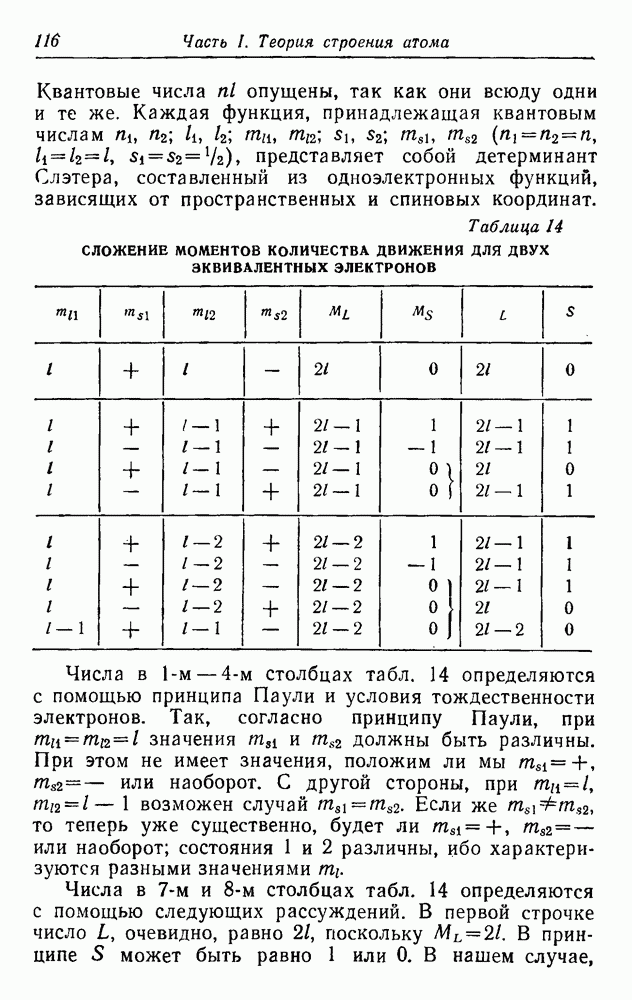
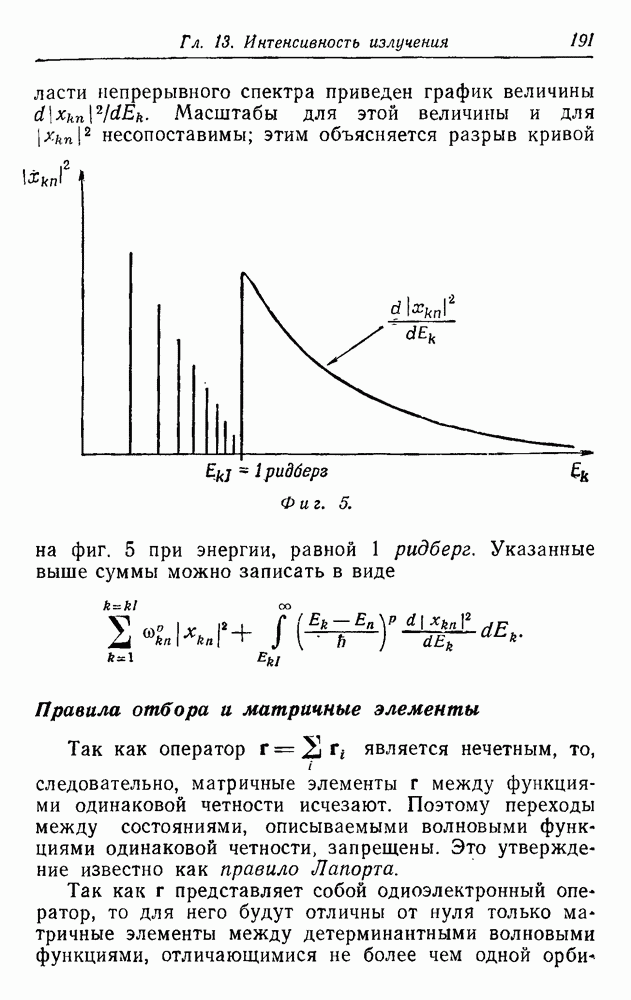
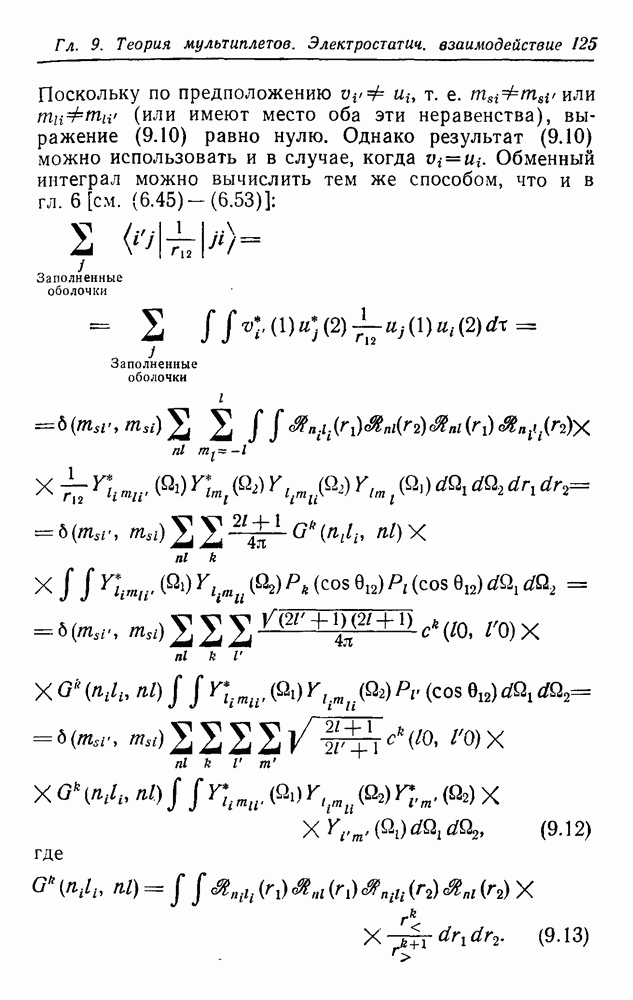| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
20. ВТОРИЧНОЕ КВАНТОВАНИЕ НЕСКОЛЬКИХ ПОЛЕЙ ЧАСТИЦ
Квантование нерелятивистского уравнения Шредингера
Можно убедиться, что плотность функции Лагранжа, приводящую к уравнению Шредингера, можно взять в виде

Оператор  -неэрмитов. Уравнение Эйлера — Лагранжа для
-неэрмитов. Уравнение Эйлера — Лагранжа для  гласит
гласит

а для 
 (20.2а)
(20.2а)
Это действительно правильные уравнения Шредингера для  . Импульс, канонически сопряженный с
. Импульс, канонически сопряженный с  есть
есть

Поскольку оператор не входит в выражение (20.1),  не имеет сопряженного ей импульса.
не имеет сопряженного ей импульса.
Плотность функции Гамильтона есть

Канонические уравнения движения имеют вид
 (20.56)
(20.56)
Легко видеть, что уравнения (20.5 а) и (20.56) вместе с определением (20.3) эквивалентны (20.2 а) и (20.26).
То обстоятельство, что  не имеет сопряженного импульса, не приводит к трудностям, поскольку оператор
не имеет сопряженного импульса, не приводит к трудностям, поскольку оператор  можно отождествить с и таким образом развить гамильтонов формализм. Это отождествление
можно отождествить с и таким образом развить гамильтонов формализм. Это отождествление  связано с тем обстоятельством, что уравнение поля — первого порядка по времени; поэтому производную
связано с тем обстоятельством, что уравнение поля — первого порядка по времени; поэтому производную  можно выразить через
можно выразить через  . В уравнении второго порядка по времени, таком, как уравнение Клейна — Гордона, как
. В уравнении второго порядка по времени, таком, как уравнение Клейна — Гордона, как  , так и
, так и  будут парами канонически-сопряженных переменных. Более того, если лагранжиан таков, что какой-нибудь сопряженный импульс остается неопределенным, и если при этом координату, сопряженную этому импульсу, нельзя выразить через другие координаты и импульсы, то весь гамильтонов формализм отказывается работать. С такой ситуацией мы столкнемся при квантовании электромагнитного поля.
будут парами канонически-сопряженных переменных. Более того, если лагранжиан таков, что какой-нибудь сопряженный импульс остается неопределенным, и если при этом координату, сопряженную этому импульсу, нельзя выразить через другие координаты и импульсы, то весь гамильтонов формализм отказывается работать. С такой ситуацией мы столкнемся при квантовании электромагнитного поля.
На основании (20.4) и (20.3) функцию Гамильтона можно записать в виде

Замечая, что V — вещественная классическая функция (не оператор), и принимая во внимание соотношение  убеждаемся в эрмитовости гамильтониана. Интегрируя по частям и пренебрегая поверхностным
убеждаемся в эрмитовости гамильтониана. Интегрируя по частям и пренебрегая поверхностным
членом, можем переписать выражение (20.6) в виде

Если функция V не зависит от времени, то гамильтониан Н есть интеграл движения.
До сих пор поле  рассматривалось как классическое,
рассматривалось как классическое,  как плотность его функции Гамильтона. Чтобы перейти к квантовой теории, введем правила перестановки. В силу (20.3) они имеют вид
как плотность его функции Гамильтона. Чтобы перейти к квантовой теории, введем правила перестановки. В силу (20.3) они имеют вид
 (20.8а)
(20.8а)
Здесь опущен аргумент t. Это означает, что оба оператора поля берутся в один и тот же момент времени — такая оговорка будет подразумеваться во всех аналогичных случаях.
Займемся теперь вычислением производной по времени от квантовомеханического оператора 

Первый коммутатор вычисляется путем интегрирования по частям, как и в случае (20.7), и оказывается равным

Здесь принято во внимание, что величины  коммутируют. Этот факт вытекает из того, что если
коммутируют. Этот факт вытекает из того, что если
 (20.106)
(20.106)
то

Чтобы убедиться в справедливости последнего равенства, представим производную с помощью предельного перехода
 (20.10 в)
(20.10 в)
Второй коммутатор есть

Здесь вторая строка вытекает из первой, ибо операторы  коммутируют. Отсюда
коммутируют. Отсюда
 (20.11 а)
(20.11 а)
Аналогично
 (20.11 6)
(20.11 6)
Видно, что уравнения классической и квантовой механики формально получаются одинаковыми. Так и должно быть, если отождествить скобки Пуассона с коммутаторами.
Следующие утверждения можно проверить, оперируя со скобками Пуассона. Коммутаторы в формулах (20.8) суть интегралы движения. Оператор N, определенный равенством
 (20.12)
(20.12)
также представляет собой интеграл движения. Отметим, что этот оператор эрмитов.
N-частичное или многочастичное представление для шредингеровского поля
Рассмотрим оператор N более подробно. Он эрмитов, значит, его собственные значения вещественны. Разложим  по полной ортонормированной системе функций
по полной ортонормированной системе функций
 (20.13а)
(20.13а)
Здесь величины а считаются операторами, зависящими от времени, а и  — обычными функциями. Поэтому в формуле (20.136) над
— обычными функциями. Поэтому в формуле (20.136) над  стоит крест, а над
стоит крест, а над  — звездочка. Пользуясь ортонормированностью функции
— звездочка. Пользуясь ортонормированностью функции  , мы можем найти амплитуды
, мы можем найти амплитуды
 (20.14а)
(20.14а)
Вычислим теперь коммутатор
 (20.15б)
(20.15б)
Далее,
 (20.16)
(20.16)
Из формулы (20.15) следует, что операторы  коммутируют друг с другом и их можно одновременно привести
коммутируют друг с другом и их можно одновременно привести
к диагональному виду
 (20.18)
(20.18)
Таким же образом
 (20.19а)
(20.19а)
До сих пор мы еще не указали, на что действуют эти операторы амплитуд поля. Они не действуют на обычные функции; мы видели, что они коммутируют с  Они действуют на вектор состояния, описывающий всю рассматриваемую квантовомеханическую систему. Из формул (20.17) и (20.18) следует, что можно выбрать ортонормированную систему таких векторов, что в осуществляемом ими представлении оператор N и все
Они действуют на вектор состояния, описывающий всю рассматриваемую квантовомеханическую систему. Из формул (20.17) и (20.18) следует, что можно выбрать ортонормированную систему таких векторов, что в осуществляемом ими представлении оператор N и все  будут диагональны. Типичный такой вектор имеет вид
будут диагональны. Типичный такой вектор имеет вид
 (20.20)
(20.20)
где символ  означает, что выражение (20.20) есть собственная функция каждого оператора
означает, что выражение (20.20) есть собственная функция каждого оператора  с собственным значением
с собственным значением  . Когда это не может привести к недоразумениям, мы будем просто обозначать собственный вектор оператора
. Когда это не может привести к недоразумениям, мы будем просто обозначать собственный вектор оператора  с собственным значением
с собственным значением  посредством
посредством  .
.
Получим теперь для операторов  и некоторые формальные соотношения, которые облегчат их интерпретацию. По определению,
и некоторые формальные соотношения, которые облегчат их интерпретацию. По определению,
 (20.21а)
(20.21а)
С помощью соотношения (20.19б) получаем

Аналогично с помощью (20.19а)
 (20.21в)
(20.21в)
Равенство (20.216) указывает, что  есть собственная функция
есть собственная функция  с собственным значением
с собственным значением  . Аналогичным образом, при действии
. Аналогичным образом, при действии  на собственную функцию
на собственную функцию  с собственным значением
с собственным значением  получается собственная функция
получается собственная функция  с собственным значением
с собственным значением  . Если считать собственные функции нормированными, то
. Если считать собственные функции нормированными, то
 (20.22а)
(20.22а)
Для определения констант составим скалярные произведения
 (20.23б)
(20.23б)
Отсюда

Операторы а и a носят соответственно названия операторов рождения и уничтожения. Фазы постоянных величин мы положили равными нулю, так что при повторном действии операторов а выполняются соотношения (20.15). (Впрочем, они выполнялись бы и при более общем выборе фазы.)
Покажем теперь, что собственные значения  суть неотрицательные целые числа
суть неотрицательные целые числа

Таким образом, собственные значения неотрицательны. Из формулы (20.24 6) видно, что если бы существовало
нецелое собственное значение, то путем повторного действия оператора  можно было бы получить собственную функцию, принадлежащую отрицательному собственному значению. Но это невозможно. Если же существуют только целые собственные значения, то равенство (20.246) не приводит к трудностям, ибо повторное действие оператора
можно было бы получить собственную функцию, принадлежащую отрицательному собственному значению. Но это невозможно. Если же существуют только целые собственные значения, то равенство (20.246) не приводит к трудностям, ибо повторное действие оператора  в конце концов приводит к собственной функции с нулевым собственным значением, а
в конце концов приводит к собственной функции с нулевым собственным значением, а 
Исследуем зависимость  от времени
от времени
 (20.26)
(20.26)
Эта величина обращается в нуль, если  при
при  . Таким образом, все операторы
. Таким образом, все операторы  суть интегралы движения в том, и только в том, случае, когда недиагональные матричные элементы h равны нулю, т. е. когда
суть интегралы движения в том, и только в том, случае, когда недиагональные матричные элементы h равны нулю, т. е. когда  суть шредингеровские собственные функции оператора
суть шредингеровские собственные функции оператора  Конечно,
Конечно,  - всегда интеграл движения, как можно убедиться, суммируя по k вторую строку равенства (20.26).
- всегда интеграл движения, как можно убедиться, суммируя по k вторую строку равенства (20.26).
Рассмотрим теперь оператор полной энергии (20.7). Подставляя туда операторы  из (20.13), получаем
из (20.13), получаем
 (20.27)
(20.27)
Если выбрать в качестве и решения одночастичного уравнения Шредингера, то
 (20.28а)
(20.28а)
В нашем представлении операторы считаются диагональными; отсюда
 (20.28б)
(20.28б)
В этом случае все  суть интегралы движения, поскольку оператор h диагонален.
суть интегралы движения, поскольку оператор h диагонален.
Для оператора полного импульса поля (не смешивать с сопряженным импульсом!) также можно получить весьма эвристичное соотношение типа (20.286). Для этого заметим прежде всего, что плотность энергии (19.19) есть  -компонента ковариантного тензора второго ранга — тензора энергии-импульса
-компонента ковариантного тензора второго ранга — тензора энергии-импульса
 (20.29)
(20.29)
 -компоненты этого тензора
-компоненты этого тензора  представляют собой плотность импульса, а пространственный интеграл от них есть импульс поля
представляют собой плотность импульса, а пространственный интеграл от них есть импульс поля
 (20.30а)
(20.30а)
Здесь  есть одночастичный оператор импульса. Если выбрать в качестве величин и собственные функции одночастичного оператора импульса (а не оператора энергии), то оператор полного импульса поля
есть одночастичный оператор импульса. Если выбрать в качестве величин и собственные функции одночастичного оператора импульса (а не оператора энергии), то оператор полного импульса поля
 (20.31)
(20.31)
При  функции и могут быть одновременно собственными функциями операторов энергии и импульса.
функции и могут быть одновременно собственными функциями операторов энергии и импульса.
Теперь мы уже в состоянии построить гильбертово пространство, в котором действуют операторы поля, и дать физическую интерпретацию наших формальных результатов. Образуем систему базисных векторов, диагонализующих все операторы  и N, следующим образом. Начнем с вектора
и N, следующим образом. Начнем с вектора  , который называется вектором состояния вакуума и обладает свойством
, который называется вектором состояния вакуума и обладает свойством
 (20.32)
(20.32)
для всех k. Существование такого вектора было доказано выше. Физическая интерпретация вакуумного состояния заключается в том, что оно описывает ситуацию, когда частицы отсутствуют. Затем построим вектор
 (20.33а)
(20.33а)
Нормирующий множитель здесь выбран в соответствии с формулами (20.24). На основании (20.216) имеем
 (20.33б)
(20.33б)
Этот вектор мы интерпретируем как одночастичное состояние. Он описывает физическую ситуацию, когда присутствует одна частица. Эту ситуацию, впрочем, можно описывать и в рамках обычной квантовой механики, теория поля здесь не обязательна. Чтобы установить связь между этими двумя описаниями, постулируем, что состояние  описывает частицу, которая находится в обычном квантовомеханическом состоянии
описывает частицу, которая находится в обычном квантовомеханическом состоянии  [см. (20.146)]. Удобное обозначение для одночастичных состояний имеет вид
[см. (20.146)]. Удобное обозначение для одночастичных состояний имеет вид
 (20.33в)
(20.33в)
Продолжая в том же духе, построим двухчастичные состояния
 (20.346)
(20.346)
Имеем
 (20.34в)
(20.34в)
Функция  соответствует двум частицам: одной в состоянии k, а другой в состоянии I; функция
соответствует двум частицам: одной в состоянии k, а другой в состоянии I; функция  - тоже двум частицам, причем обе находятся в состоянии k. Нормировочные коэффициенты опять-таки находятся на основании (20.24). Обозначения в левой части (20.34а) и (20.34б) указывают как на число присутствующих частиц, так и на занятые состояния. Отметим, что данная теория не накладывает ограничений
- тоже двум частицам, причем обе находятся в состоянии k. Нормировочные коэффициенты опять-таки находятся на основании (20.24). Обозначения в левой части (20.34а) и (20.34б) указывают как на число присутствующих частиц, так и на занятые состояния. Отметим, что данная теория не накладывает ограничений
на число частиц, которые могут находиться в одном и том же состоянии; таким образом, мы имеем дело с бозонами. Фермионы будут рассмотрены ниже. При установлении связи с обычной квантовой механикой надо принять во внимание свойство симметрии волновой функции. Состояние  соответствует функции
соответствует функции

а состояние  — функции
— функции

Путем повторного действия операторов рождения на состояние вакуума можно построить все базисные векторы теории: вектор
 (20.35а)
(20.35а)
описывает  частиц, причем все они находятся в состоянии
частиц, причем все они находятся в состоянии  вектор
вектор

описывает  частиц, в том числе
частиц, в том числе  частиц в состоянии
частиц в состоянии  частиц в состоянии 2 и т. д.
частиц в состоянии 2 и т. д.
На основании полученной физической интерпретации и установленного выше соответствия с классической механикой заключаем, что N есть оператор, собственные значения которого равны числу имеющихся частиц. Вспомнив определение этого оператора (20.12), приходим к выводу, что если считать  классической плотностью заряда, то, согласно теории поля, полный заряд системы частиц должен быть кратен е. Оператор
классической плотностью заряда, то, согласно теории поля, полный заряд системы частиц должен быть кратен е. Оператор  описывает число частиц в состоянии k, Аналогично
описывает число частиц в состоянии k, Аналогично
собственные значения Н и Р дают полную энергию и импульс системы.
Если  суть собственные функции, удовлетворяющие одночастичному уравнению Шредингера, то теория поля дает стационарные решения, в которых число частиц в
суть собственные функции, удовлетворяющие одночастичному уравнению Шредингера, то теория поля дает стационарные решения, в которых число частиц в  состоянии равно
состоянии равно  а полная энергия есть
а полная энергия есть  Если система свободна, то оператор Р также
Если система свободна, то оператор Р также  диагонален, и полный импульс есть
диагонален, и полный импульс есть 
Обычно в теории поля говорят, что оператор  действуя на состояние вакуума, создает частицу в состоянии k [подробнее: частицу, описываемую функцией
действуя на состояние вакуума, создает частицу в состоянии k [подробнее: частицу, описываемую функцией  ]. Точно так же оператор
]. Точно так же оператор  действуя на состояние вакуума, создает частицу в точке
действуя на состояние вакуума, создает частицу в точке  . Чтобы убедиться в этом, напишем
. Чтобы убедиться в этом, напишем
 (20.36)
(20.36)
Каждая собственная функция  соответствует частице в состоянии
соответствует частице в состоянии  (Переменная, характеризующая положение частицы, снабжена штрихом, так как это есть индекс суммирования, который следует отличать от аргумента функции
(Переменная, характеризующая положение частицы, снабжена штрихом, так как это есть индекс суммирования, который следует отличать от аргумента функции  ) Таким образом, вектор
) Таким образом, вектор  соответствует сумме
соответствует сумме

Это есть волновая функция частицы, локализованной в точке  .
.
Напомним еще раз, что все наше рассмотрение относится к некоторому избранному моменту времени t. Чтобы определить зависимость от времени, которую дает теория, обычно пользуются картиной Гейзенберга. При этом волновая функция остается не зависящей  времени, а зависимость операторов от времени определяется гамильтонианом Н. Следует заметить, что то или иное представление задается условном диагональности некоторого оператора. Иными словами, чтобы определить представление, недостаточно одних лишь правил
времени, а зависимость операторов от времени определяется гамильтонианом Н. Следует заметить, что то или иное представление задается условном диагональности некоторого оператора. Иными словами, чтобы определить представление, недостаточно одних лишь правил
перестановки; мы, в частности, требуем, чтобы были диагональными операторы  и, следовательно, оператор
и, следовательно, оператор 
Теория поля привела нас к теории Шредингера для системы многих бозонов. Однако мы неявно предполагали частицы невзаимодействующими: в операторе Гамильтона отсутствуют члены типа собственной энергии — имеется только взаимодействие с внешним потенциалом. Как показали Йордан и Вигнер [48], эти два подхода — задача многих бозонов в теории Шредингера и теория вторично квантованного поля — полностью эквивалентны и при учете взаимодействия.
В заключение расщепим  на два эрмитовых оператора:
на два эрмитовых оператора:
 (20.37)
(20.37)
Тогда

Мы видим, что соотношения (20.38) имеют такой же вид, как и для гармонического осциллятора [с очевидным законом соответствия между величинами (20.38) и параметрами, характеризующими осциллятор]. С помощью этого обстоятельства можно было бы и иным методом прийти к полученным выше результатам [1].
Фермионы и соотношения антикоммутации
Мы видели, что квантование шредингеровского поля с помощью обычного принципа соответствия между коммутатором и скобкой Пуассона привело к системе многих бозонов. Анализируя проделанные выше выкладки, можно установить, что вывод о том, что  могут иметь любые неотрицательные целочисленные значения, вытекает, по существу, из правил перестановки (20.8), (20.15) или (20.38). Йордан и Вигнер [48] обнаружили,
могут иметь любые неотрицательные целочисленные значения, вытекает, по существу, из правил перестановки (20.8), (20.15) или (20.38). Йордан и Вигнер [48] обнаружили,
что замена коммутаторов антикоммутаторами приводит к системе многих фермионов. Затем Паули [50] показал, что если квантовая теория поля удовлетворяет перечисленным ниже условиям, то фермионы должны квантоваться с помощью антикоммутаторов, а бозоны — с помощью коммутаторов. Условия Паули таковы:
1. Коммутатор двух наблюдаемых величин, относящихся к двум точкам пространства — времени, разделенным пространственно-подобным интервалом, должен быть равен нулю. В противном случае эти величины нельзя было бы одновременно измерить с произвольной точностью, откуда следовало бы, что возмущение распространяется в пространстве со скоростью, превышающей скорость света.
2. Энергия поля должна быть неотрицательной. Чтобы выполнить нашу программу для нерелятивистского уравнения Шредингера, заменим равенства (20.8) и (20.15) на
 (20.39а)
(20.39а)
где
 (20.40в)
(20.40в)
Определяя операторы  как и выше, можем убедиться, что все они коммутируют друг с другом и, следовательно, могут быть диагонализованы одновременно. С помощью соотношения (20.406) мы получаем
как и выше, можем убедиться, что все они коммутируют друг с другом и, следовательно, могут быть диагонализованы одновременно. С помощью соотношения (20.406) мы получаем
 (20.41)
(20.41)
Здесь принято во внимание, что, в силу (20.40а),  Таким образом, собственные значения
Таким образом, собственные значения  в соответствии с принципом Паули равны 0 или 1.
в соответствии с принципом Паули равны 0 или 1.
Операторы  не могут быть диагонализованы. Действительно, если бы оператор
не могут быть диагонализованы. Действительно, если бы оператор  был диагонален, то, в силу (20.40а), его собственные значения были бы равны нулю; тогда выражение
был диагонален, то, в силу (20.40а), его собственные значения были бы равны нулю; тогда выражение  также обратилось бы в нуль, что противоречит равенству (20.40б). Собственные значения М — суть неотрицательные целые числа.
также обратилось бы в нуль, что противоречит равенству (20.40б). Собственные значения М — суть неотрицательные целые числа.
Легко убедиться, что полученные выше выражения для полных энергии и импульса остаются неизменными.
Мы сохранили гейзенберговское выражение для зависимости оператора от времени. Можно убедиться, что в этом случае уравнения движения (20.9) остаются неизменными. Легко проверить, что  сохраняют смысл соответственно операторов рождения и уничтожения частиц. Именно, удобно выбрать эти операторы так, чтобы выполнялись равенства
сохраняют смысл соответственно операторов рождения и уничтожения частиц. Именно, удобно выбрать эти операторы так, чтобы выполнялись равенства
 (20.42а)
(20.42а)
Легко видеть при этом, что, в силу (20.41),

Отсюда явствует, что соотношение (20.40) при  действительно выполняется. Фазу величины
действительно выполняется. Фазу величины  необходимо и достаточно выбрать так, чтобы соотношение (20.40) выполнялось и при
необходимо и достаточно выбрать так, чтобы соотношение (20.40) выполнялось и при  . Если
. Если  топри действии оператора
топри действии оператора  знак Ой меняется, так как при этом
знак Ой меняется, так как при этом  заменяется на
заменяется на  но при действии оператора
но при действии оператора  ; остается неизменным. Этого как раз достаточно, чтобы выполнялось соотношение
; остается неизменным. Этого как раз достаточно, чтобы выполнялось соотношение  .
.
Квантование уравнения Дирака
Плотность функции Лагранжа для уравнения Дирака можно взять в виде
 (20.43)
(20.43)
Варьируя по каждой из компонент  получаем четыре уравнения Эйлера — Лагранжа, которые можно компактно записать в виде
получаем четыре уравнения Эйлера — Лагранжа, которые можно компактно записать в виде
 (20.44а)
(20.44а)
Аналогично варьирование по четырем компонентам  дает
дает
 (20.446)
(20.446)
Это есть не что иное, как уравнения движения для дираковского поля (17.19) и (17.206). Импульс, сопряженный обобщенной координате  есть
есть
 (20.45а)
(20.45а)
Следует помнить, что  суть четырехкомпонентные спиноры и, следовательно, уравнение (20.45а) есть компактная запись четырех уравнений
суть четырехкомпонентные спиноры и, следовательно, уравнение (20.45а) есть компактная запись четырех уравнений
 (20.456)
(20.456)
Видно далее, что  не имеет сопряженного импульса. Плотность функции Гамильтона есть
не имеет сопряженного импульса. Плотность функции Гамильтона есть
 (20.46а)
(20.46а)
Гамильтониан имеет вид
 (20.46б)
(20.46б)
Чтобы убедиться в эрмитовости гамильтониана, проинтегрируем половину первого слагаемого по частям и пренебрежем поверхностным членом
 (20.46в)
(20.46в)
Поскольку мы желаем описывать фермионы, будем квантовать поля с помощью соотношений антикоммутации
С помощью (20.456) условия квантования можно представить в виде
 (20.47а)
(20.47а)
Обозначение  несколько произвольно. Фактически
несколько произвольно. Фактически  есть столбец из четырех операторов
есть столбец из четырех операторов  — строка из четырех операторов
— строка из четырех операторов 
Уравнение движения для оператора  имеет вид
имеет вид
 (20.48а)
(20.48а)
Выпишем явно существенную часть первого слагаемого в коммутаторе
 (20.48б)
(20.48б)
Для второго слагаемого получаем

Суммируя, находим
 (20.48г)
(20.48г)
Это есть уравнение поля Дирака. Можно убедиться, что оператор  также удовлетворяет соответствующему уравнению поля.
также удовлетворяет соответствующему уравнению поля.
Оператор числа частиц N определяется, как и выше,

Можно убедиться, что он представляет собой интеграл движения.
Многочастичное представление для поля Дирака
Удобно разложить дираковские волновые амплитуды  по плоским волнам. Поскольку для каждого значения импульса к существуют четыре линейно независимых решения, мы будем приписывать им индекс
по плоским волнам. Поскольку для каждого значения импульса к существуют четыре линейно независимых решения, мы будем приписывать им индекс  , принимающий значения 1, 2, 3, 4. Имеем
, принимающий значения 1, 2, 3, 4. Имеем
 (20.49а)
(20.49а)
Амплитуды  определяются формулами (18.6) и (18.7); мы считаем функции нормированными в объеме
определяются формулами (18.6) и (18.7); мы считаем функции нормированными в объеме  . Из общей теории следует, что соотношения ортогональности и нормировки должны иметь вид
. Из общей теории следует, что соотношения ортогональности и нормировки должны иметь вид
 (20.49б)
(20.49б)
Разложим спинорные волновые функции
 (20.50а)
(20.50а)
Здесь  — комплексно-сопряженный транспонированный спинор. (Мы не пользуемся здесь крестом; этот
— комплексно-сопряженный транспонированный спинор. (Мы не пользуемся здесь крестом; этот
символ будет употребляться лишь применительно к операторам, в то время как v есть классическая функция.) Соотношения антикоммутации (20.47) и условие ортогональности и нормировки (20.496) дают
 (20.51а)
(20.51а)
где отсутствие аргумента t указывает на то, что вычисляются коммутаторы величин, взятых в один и тот же момент времени. Оператор числа частиц есть
 (20.52)
(20.52)
Из общей теории, изложенной выше, известно, что собственные значения  равны 0 или 1; таким образом, как мы и желали, дираковские частицы представляют собой фермионы.
равны 0 или 1; таким образом, как мы и желали, дираковские частицы представляют собой фермионы.
Полная энергия, вычисленная по формуле (20.466),
 (20.53а)
(20.53а)
Функция v удовлетворяет уравнению
 (20.536)
(20.536)
Отсюда

Полный импульс вычисляется по формуле (20.30а) с учетом того обстоятельства, что величины  следует теперь считать соответственно строкой и столбцом. Получаем
следует теперь считать соответственно строкой и столбцом. Получаем
 (20.54а)
(20.54а)
Проделав те же алгебраические выкладки, что и выше, можем преобразовать выражение (20.54а) к виду

Позитроны
Как видно из формулы (20.53в), энергия поля может стать сколь угодно большой по абсолютной величине и притом отрицательной: уравнение Дирака имеет решения с отрицательной энергией  . Эта трудность преодолевается с помощью дираковского определения вакуума (см. стр. 271), которое теперь можно переписать в виде
. Эта трудность преодолевается с помощью дираковского определения вакуума (см. стр. 271), которое теперь можно переписать в виде
 (20.55)
(20.55)
Поскольку, далее, считается, что заполненные состояния с отрицательной энергией не приводят к наблюдаемым эффектам, мы вычтем их вклад в энергию и импульс. Иными словами, переопределим наблюдаемые энергию и импульс следующим образом:
 (20.56а)
(20.56а)
На основании (20.53в) и (20.546) получаем
 (20.57а)
(20.57а)
Определим новый оператор
 (20.58)
(20.58)
который имеет собственное значение 1, когда состояние  незаполнено, и 0, когда оно заполнено. Тогда равенства (20.57) можно переписать в виде
незаполнено, и 0, когда оно заполнено. Тогда равенства (20.57) можно переписать в виде
 (20.59а)
(20.59а)
При таком определении энергия всегда неотрицательна. Более того, согласно (20.59а), отсутствующий электрон с отрицательной энергией дает в полную энергию положительный вклад. Естественно ожидать, что такая «дырка» ведет себя как физическая частица. Как отмечалось выше, при рассмотрении уравнения Дирака считается, что такие «дырки» представляют собой позитроны.
Из формулы (20.596) видно, что импульс позитрона есть  (электрон с импульсом
(электрон с импульсом  отсутствует). Скорость позитрона
отсутствует). Скорость позитрона

т. e. она равна скорости электрона в незаполненном состоянии.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Часть I. ТЕОРИЯ СТРОЕНИЯ АТОМА
- 1. УРАВНЕНИЕ ШРЕДИНГЕРА И ПРИБЛИЖЕННЫЕ МЕТОДЫ ЕГО РЕШЕНИЯ
- 2. ИНТЕГРАЛЫ ДВИЖЕНИЯ
- 3. ТОЖДЕСТВЕННОСТЬ ЧАСТИЦ И СИММЕТРИЯ
- 4. ДВУХЭЛЕКТРОННЫЕ АТОМЫ. РАСЧЕТ ПО ТЕОРИИ ВОЗМУЩЕНИЙ
- 5. ДВУХЭЛЕКТРОННЫЕ АТОМЫ. РАСЧЕТ ВАРИАЦИОННЫМ МЕТОДОМ
- 6. САМОСОГЛАСОВАННОЕ ПОЛЕ
- 7. СТАТИСТИЧЕСКАЯ МОДЕЛЬ ТОМАСА—ФЕРМИ
- 8. ТЕОРИЯ МУЛЬТИПЛЕТОВ. СЛОЖЕНИЕ МОМЕНТОВ
- 9. ТЕОРИЯ МУЛЬТИПЛЕТОВ. ЭЛЕКТРОСТАТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ
- 10. ТЕОРИЯ МУЛЬТИПЛЕТОВ. МАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ
- 11. МОЛЕКУЛЫ
- 12. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ ИЗЛУЧЕНИЯ
- 13. ИНТЕНСИВНОСТЬ ИЗЛУЧЕНИЯ
- 14. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
- 15. СТОЛКНОВЕНИЯ АТОМОВ С ЗАРЯЖЕННЫМИ ЧАСТИЦАМИ
- Часть II. РЕЛЯТИВИСТСКИЕ ТЕОРИИ
- 16. УРАВНЕНИЕ КЛЕЙНА—ГОРДОНА
- 17. УРАВНЕНИЕ ДИРАКА. ФОРМАЛЬНАЯ ТЕОРИЯ
- 18. РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА
- Часть III. ВВЕДЕНИЕ В ТЕОРИЮ ПОЛЯ
- 19. КВАНТОВАНИЕ ПОЛЯ
- 20. ВТОРИЧНОЕ КВАНТОВАНИЕ НЕСКОЛЬКИХ ПОЛЕЙ ЧАСТИЦ
- 21. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ. КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- ЛИТЕРАТУРА