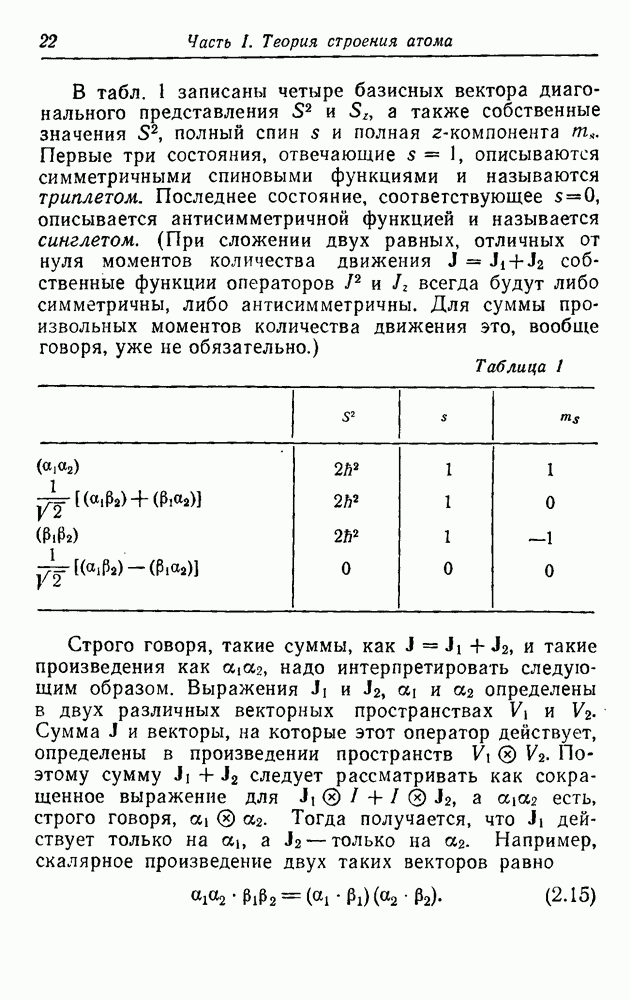
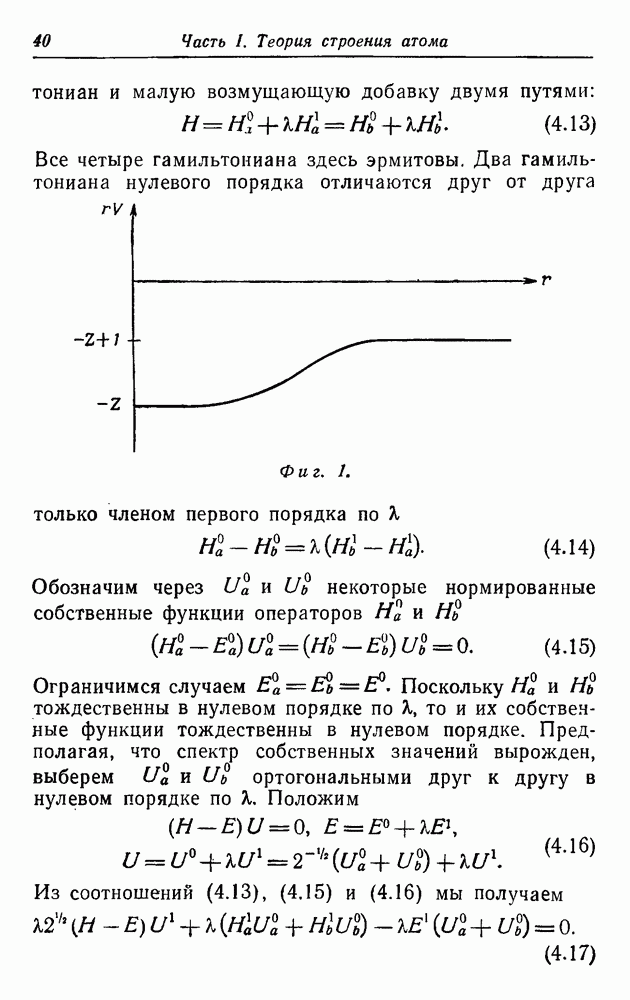
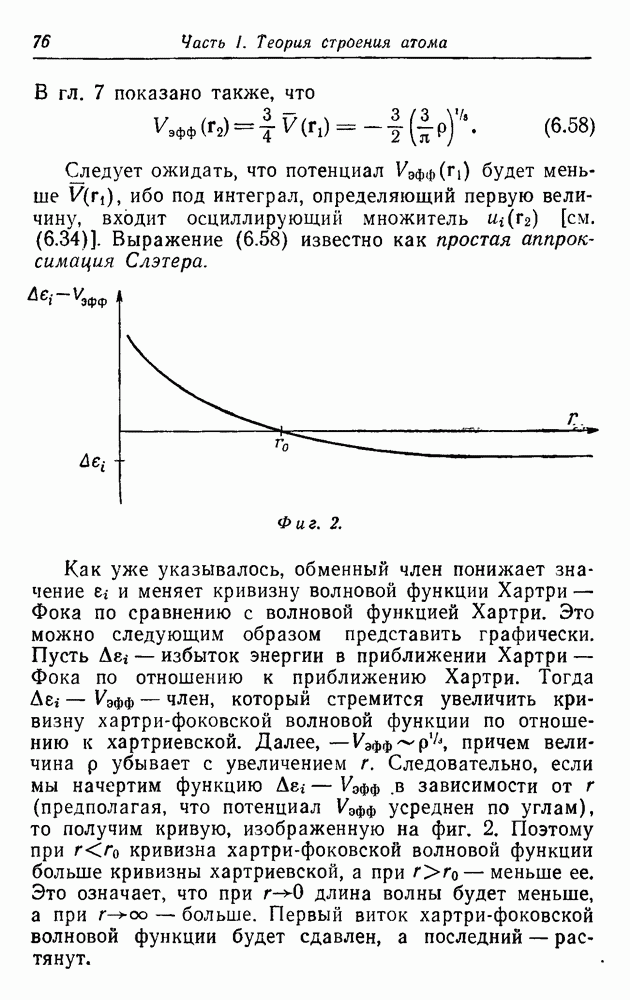
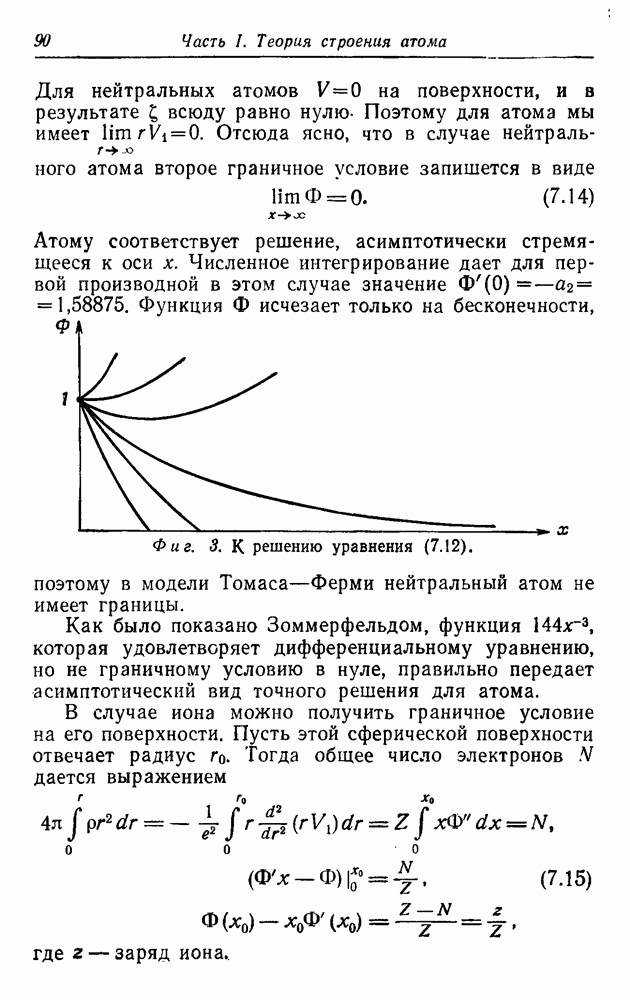
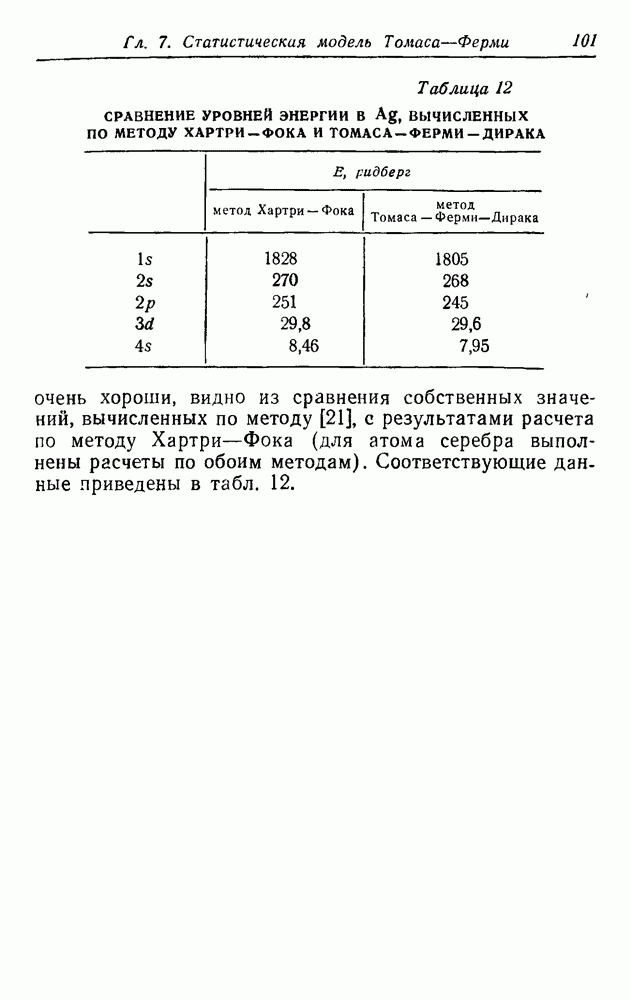
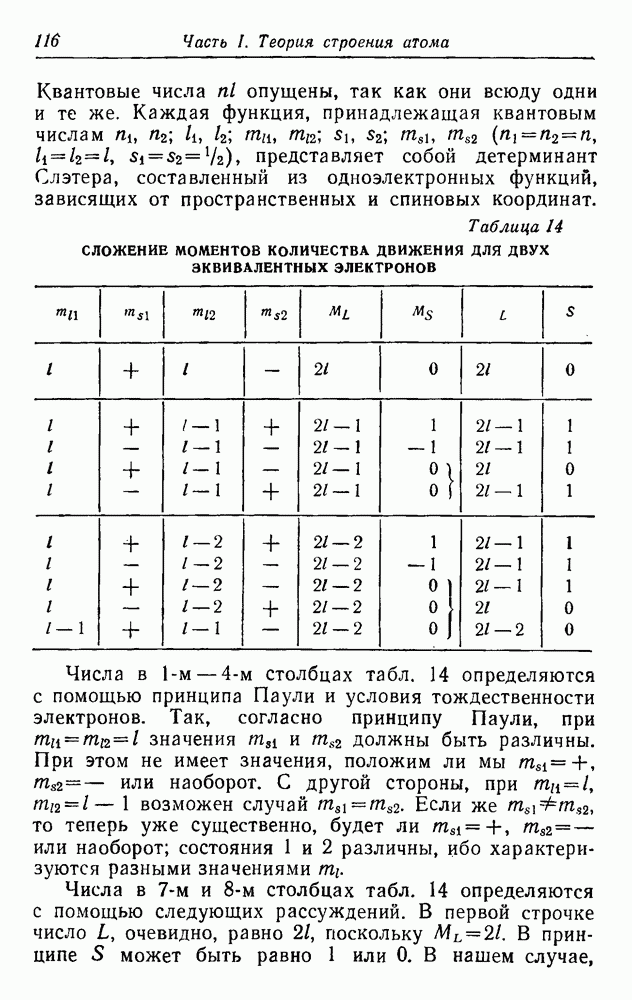
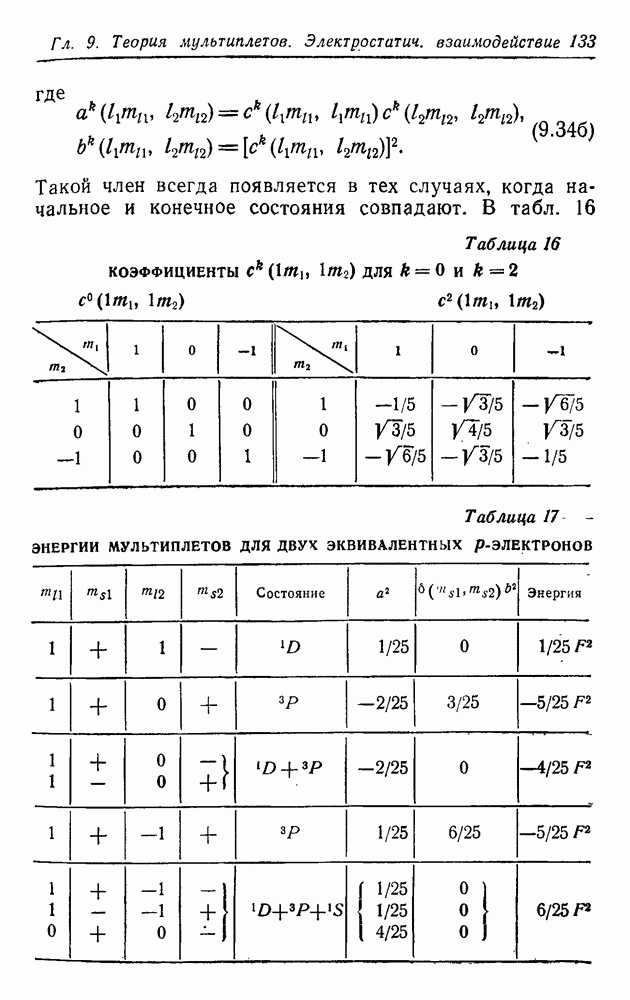
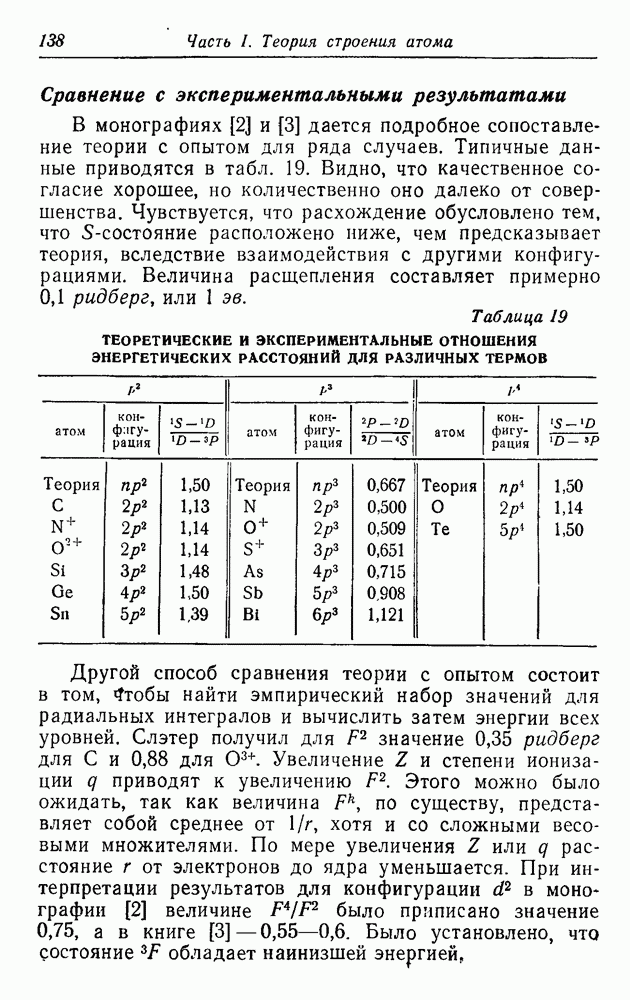
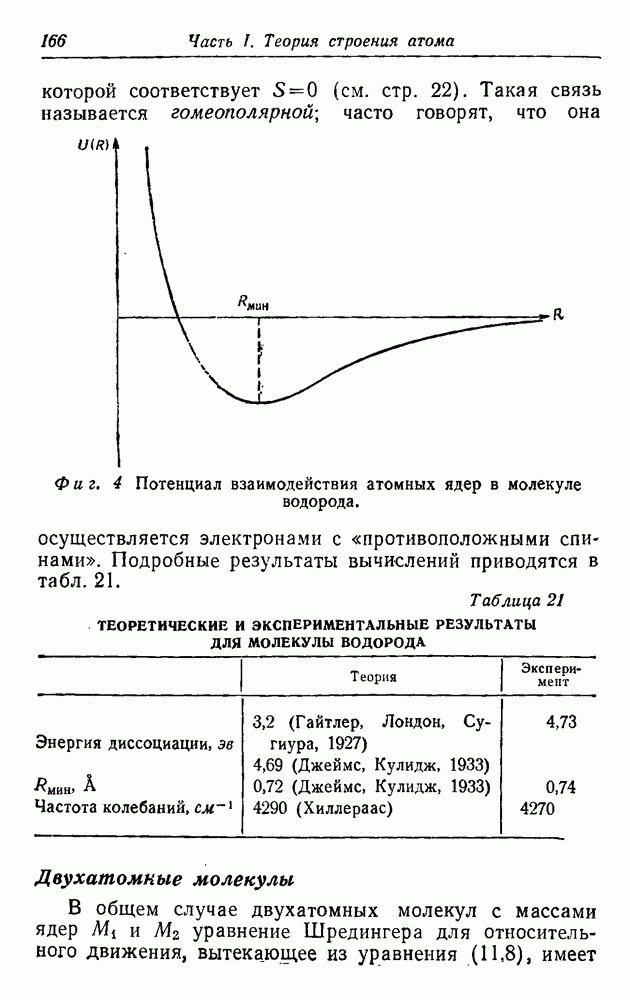
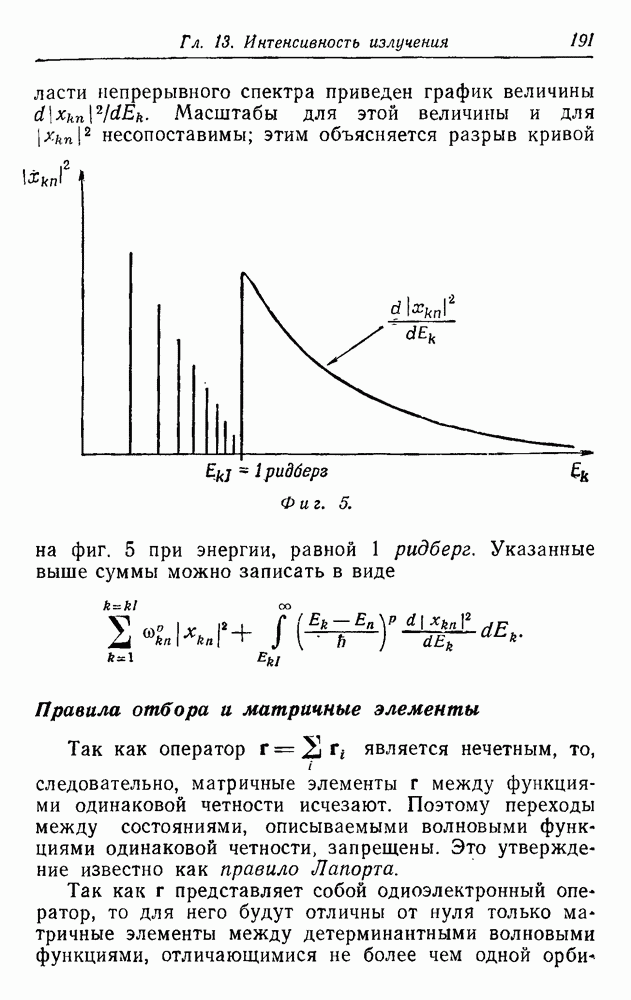
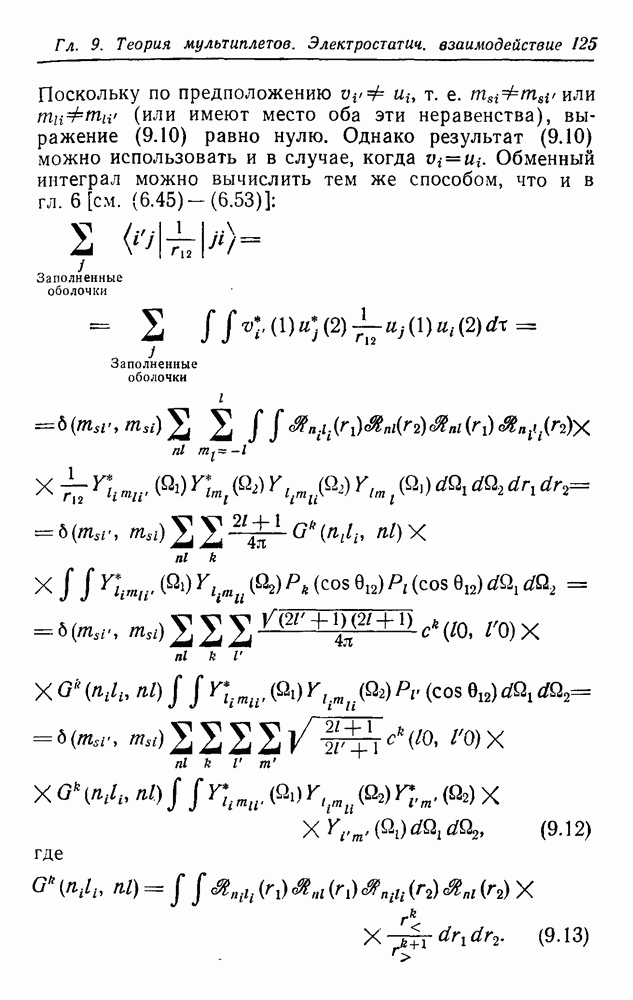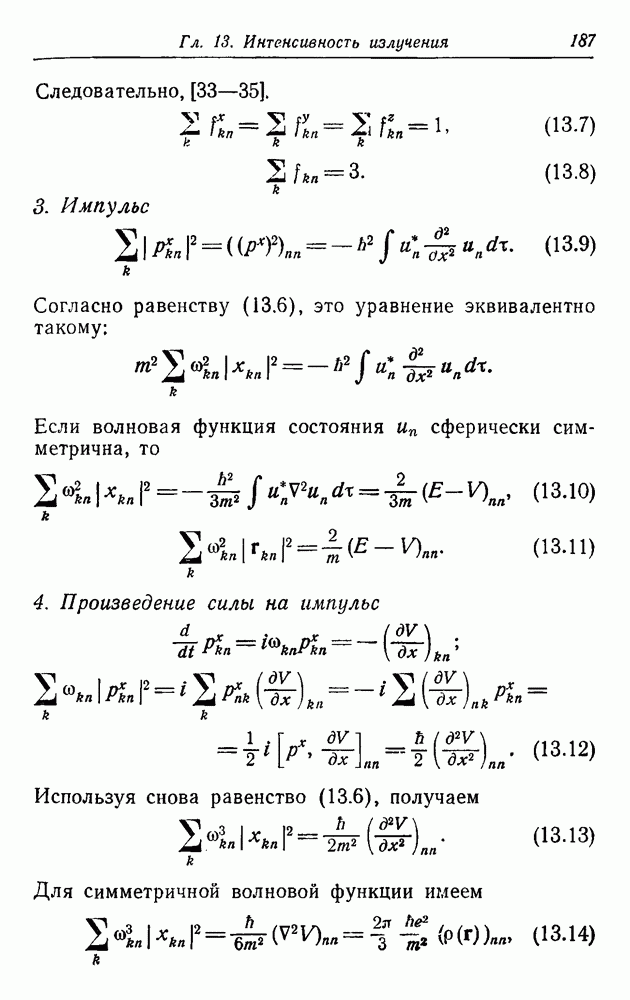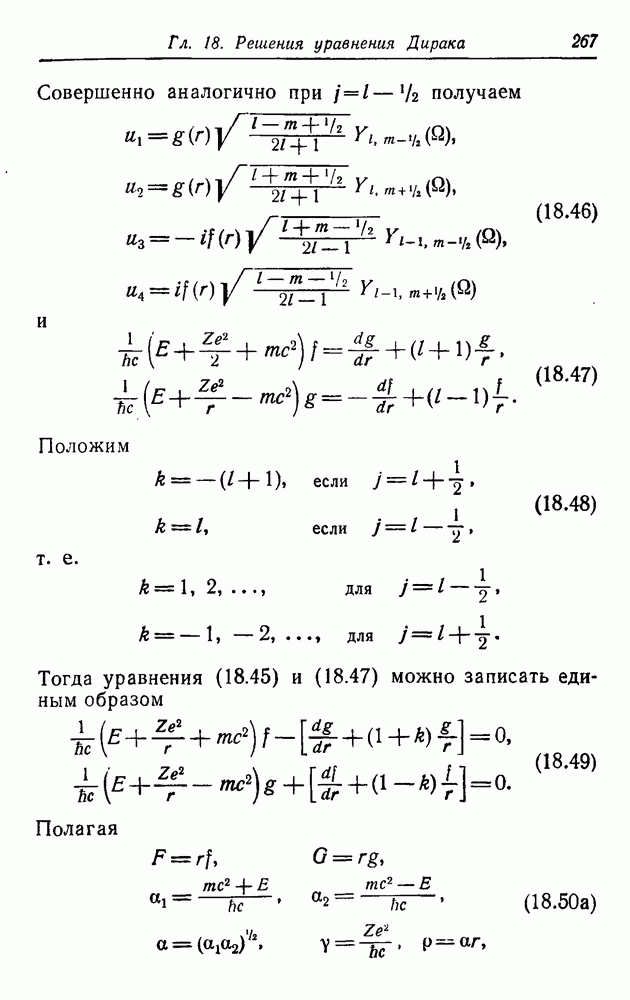| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
17. УРАВНЕНИЕ ДИРАКА. ФОРМАЛЬНАЯ ТЕОРИЯ
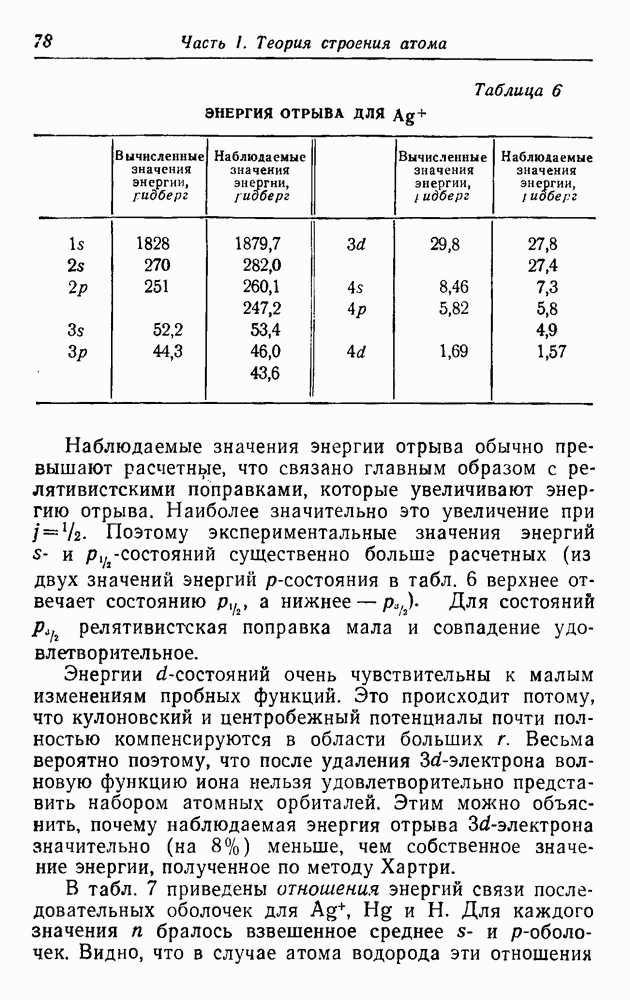
В своей работе [39], несомненно принадлежащей к числу крупнейших физических исследований, выполненных в нашем столетии, Дирак получил релятивистское волновое уравнение, свободное от трудности с отрицательной плотностью состояний. До тех пор, пока Паули и Вейсскопф не дали новой интерпретации уравнения Клейна — Гордона, считалось, что уравнение Дирака является единственным правильным релятивистским уравнением. Теперь мы знаем, что и уравнение Дирака и уравнение Клейна — Гордона одинаково верны; уравнение Дирака описывает частицы со спином  а уравнение Клейна — Гордона соответствует частицам с нулевым спином. Два этих уравнения описывают большинство известных элементарных частиц (хотя самоопределение понятия «элементарная частица» недавно было подвергнуто сомнению). Можно формально развить идеи теории Дирака применительно к описанию частиц ненулевой массы покоя с большими значениями спина, но эти теории не имеют успеха, так как учет взаимодействия с электромагнитным полем приводит в них к неустранимым расходимостям. Мы не будем рассматривать ни такого типа обобщений, ни оказавшихся удачными уравнений Вейля [40], описывающих релятивистские частицы с нулевой массой покоя и спином
а уравнение Клейна — Гордона соответствует частицам с нулевым спином. Два этих уравнения описывают большинство известных элементарных частиц (хотя самоопределение понятия «элементарная частица» недавно было подвергнуто сомнению). Можно формально развить идеи теории Дирака применительно к описанию частиц ненулевой массы покоя с большими значениями спина, но эти теории не имеют успеха, так как учет взаимодействия с электромагнитным полем приводит в них к неустранимым расходимостям. Мы не будем рассматривать ни такого типа обобщений, ни оказавшихся удачными уравнений Вейля [40], описывающих релятивистские частицы с нулевой массой покоя и спином  или 1. Первое из них, соответствующее нейтрино, можно рассматривать как естественный результат упрощения уравнения Дирака.
или 1. Первое из них, соответствующее нейтрино, можно рассматривать как естественный результат упрощения уравнения Дирака.
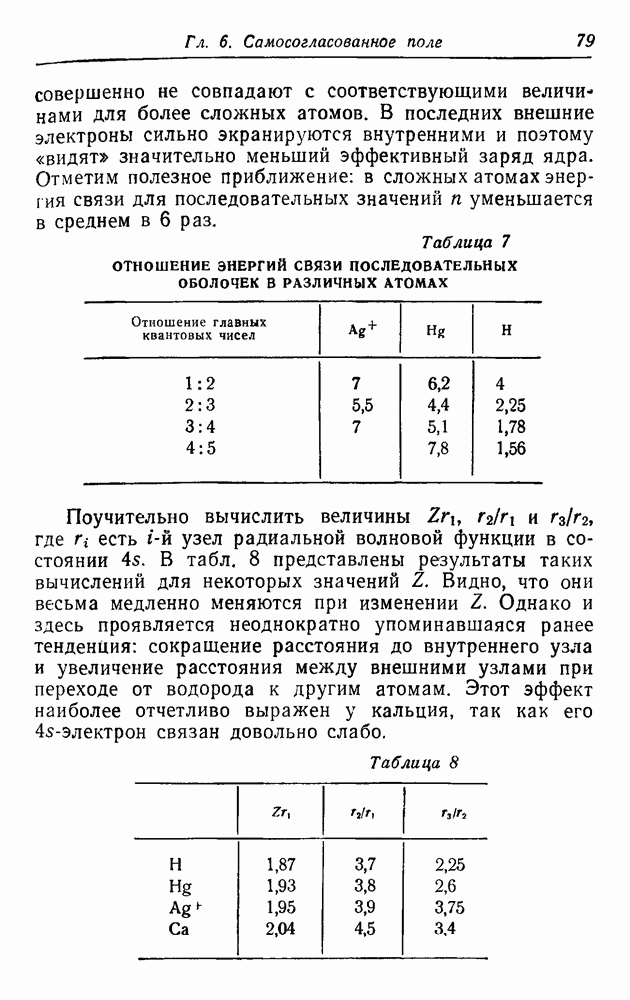
Вывод уравнения Дирака
Чтобы не допустить появления отрицательных плотностей вероятности, нужно, чтобы в выражении для  не было производных по времени. Следовательно, в
не было производных по времени. Следовательно, в
волновом уравнении не должно быть производных по времени выше первого порядка. Поскольку в теории относительности координаты  рассматриваются симметрично, волновая функция Дирака
рассматриваются симметрично, волновая функция Дирака  должна удовлетворять дифференциальному уравнению первого порядка по всем четырем координатам. Далее, уравнение обязано быть линейным, в противном случае нарушился бы квантовомеханический принцип суперпозиции. Кроме того, принцип соответствия требует, чтобы удовлетворялось уравнение Клейна — Гордона, ибо это означает просто, что справедливо уравнение (16.2), т. е. что в предельном случае больших квантовых чисел справедлива классическая релятивистская теория.
должна удовлетворять дифференциальному уравнению первого порядка по всем четырем координатам. Далее, уравнение обязано быть линейным, в противном случае нарушился бы квантовомеханический принцип суперпозиции. Кроме того, принцип соответствия требует, чтобы удовлетворялось уравнение Клейна — Гордона, ибо это означает просто, что справедливо уравнение (16.2), т. е. что в предельном случае больших квантовых чисел справедлива классическая релятивистская теория.
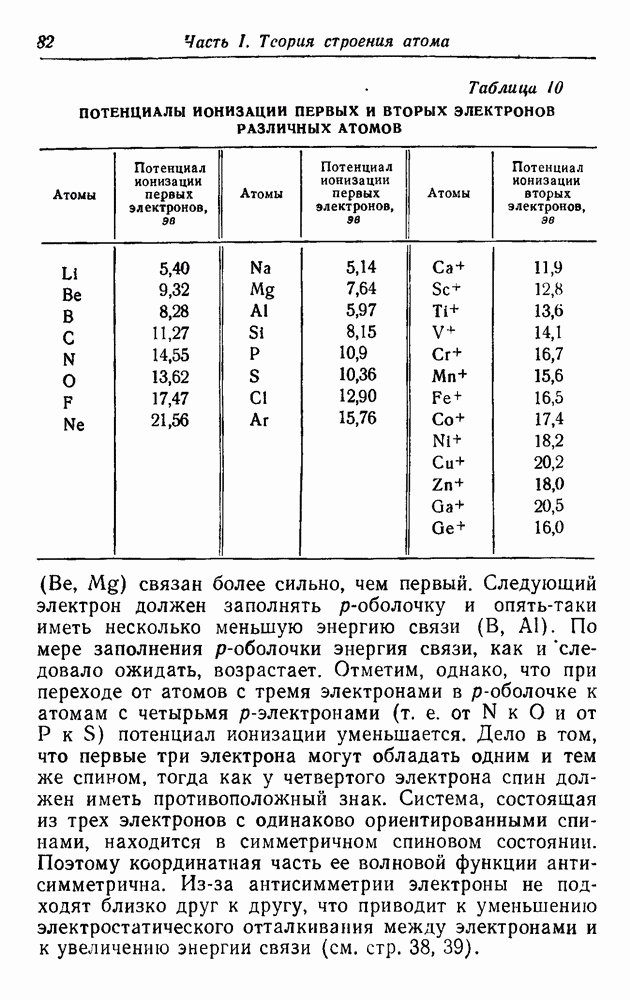
Подобная ситуация имеет место в электродинамике. Уравнения Максвелла — первого порядка по пространственным координатам и по времени. С другой стороны, каждая компонента поля удовлетворяет волновому уравнению второго порядка, аналогичному уравнению (16.3), но с нулевой массой покоя. Эти два требования не противоречат друг другу благодаря тому обстоятельству, что каждое из уравнений Максвелла связывает различные компоненты поля. Такую структуру можно принять в качестве руководящего принципа при выводе уравнения Дирака.
Допустим, что волновая функция  состоит из N компонент
состоит из N компонент  конкретного значения N мы пока не задаем. Наиболее общее уравнение, удовлетворяющее перечисленным выше требованиям, можно записать в виде
конкретного значения N мы пока не задаем. Наиболее общее уравнение, удовлетворяющее перечисленным выше требованиям, можно записать в виде

Для свободной частицы все точки пространства и все моменты времени эквивалентны (однородность пространства—времени). Поэтому величины  должны быть безразмерными константами, не зависящими от
должны быть безразмерными константами, не зависящими от  и коммутирующими с ними.
и коммутирующими с ними.
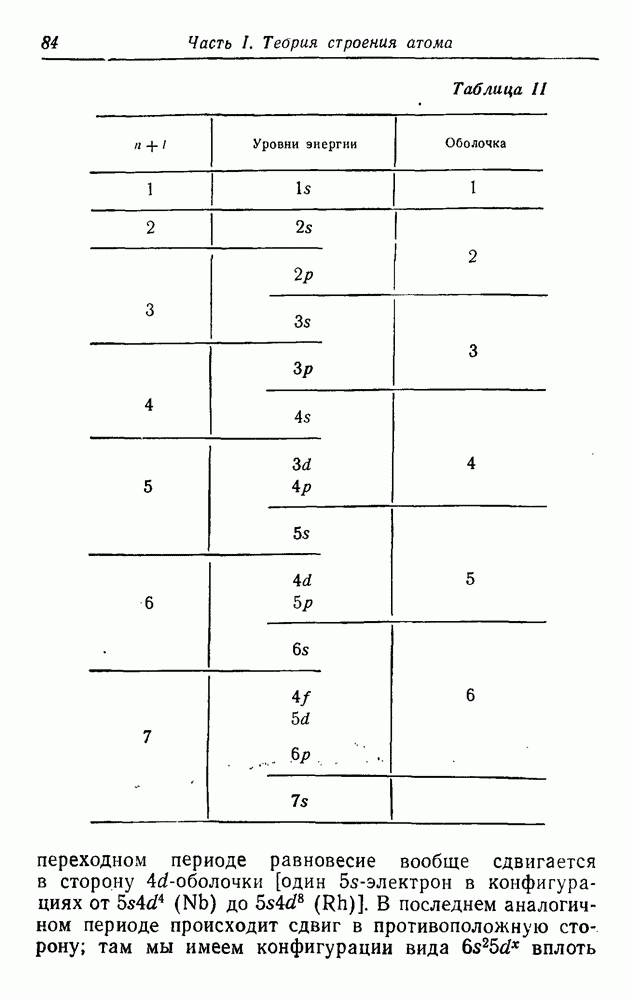
Все N уравнений (17.1) можно записать в более компактном виде, введя матрицу, состоящую из одного
столбца,

и квадратные матрицы порядка  . Далее, можно определить векторную матрицу
. Далее, можно определить векторную матрицу

Тогда система уравнений (17.1) принимает следующий вид:

Наличие N компонент у волновой функции  должно соответствовать новой степени свободы частицы, подобно тому как компоненты максвелловского поля описывают поляризацию светового кванта. Ниже мы увидим, что роль этой новой степени свободы играет спин частицы.
должно соответствовать новой степени свободы частицы, подобно тому как компоненты максвелловского поля описывают поляризацию светового кванта. Ниже мы увидим, что роль этой новой степени свободы играет спин частицы.
Попытаемся теперь найти такие выражения для плотности вероятности  и плотности тока j, которые удовлетворяли бы приведенным выше условиям и требованию положительной определенности
и плотности тока j, которые удовлетворяли бы приведенным выше условиям и требованию положительной определенности  . Положим, по определению,
. Положим, по определению,

где  — величина, эрмитово-сопряженная столбцу компонент
— величина, эрмитово-сопряженная столбцу компонент  , т. е. матрица из одной строки и N столбцов, компоненты которой комплексно сопряжены соответствующим компонентам
, т. е. матрица из одной строки и N столбцов, компоненты которой комплексно сопряжены соответствующим компонентам  . Очевидно,
. Очевидно,  подчиняется уравнению
подчиняется уравнению 

Здесь надо было изменить взаимное расположение волновой функции  и матриц
и матриц  так как матрица
так как матрица  состоит из одной строки.
состоит из одной строки.
Чтобы получить выражение для j, напишем уравнение непрерывности

Умножая уравнение (17.2) слева на  уравнение (17.4) справа на
уравнение (17.4) справа на  и складывая результаты, мы получаем
и складывая результаты, мы получаем

Чтобы это уравнение тождественно совпадало с (17.5), потребуем выполнения следующих равенств:

Соотношения (17.7) выражают совершенно естественное условие эрмитовости матриц Дирака. То, что они действительно необходимы, следует из того факта, что уравнение (17.2) можно записать в виде
 (17.10)
(17.10)
Ясно, что если оператор Я должен быть эрмитовым, то этим свойством должны обладать матрицы  . Определения (17.3) и (17.8) дают наиболее простые выражения для плотности вероятности и тока, удовлетворяющие уравнению непрерывности.
. Определения (17.3) и (17.8) дают наиболее простые выражения для плотности вероятности и тока, удовлетворяющие уравнению непрерывности.
Матрицы Дирака. I
Чтобы найти дальнейшие свойства матриц Дирака, подействуем на уравнение (17.2) оператором

Получим

Мы симметризовали здесь произведение  , что вполне допустимо, ибо операторы
, что вполне допустимо, ибо операторы  коммутируют. Чтобы матричное уравнение (17.11) согласовывалось с уравнением Клейна — Гордона для каждой компоненты волновой функции, матрицы Дирака обязаны удовлетворять условиям
коммутируют. Чтобы матричное уравнение (17.11) согласовывалось с уравнением Клейна — Гордона для каждой компоненты волновой функции, матрицы Дирака обязаны удовлетворять условиям
 (17.12)
(17.12)
где  — единичная матрица.
— единичная матрица.
Докажем теперь две важные теоремы относительно матриц Дирака. Согласно (17.12), можем написать
 (17.13 а)
(17.13 а)
Составим детерминанты матриц, фигурирующих в правой и левой частях (17.13 а),
 (17.13 б)
(17.13 б)
Условия (17.12) показывают, что матрицы  имеют обратные матрицы, поэтому ни один из детерминантов в нуль не обращается, и мы получаем
имеют обратные матрицы, поэтому ни один из детерминантов в нуль не обращается, и мы получаем

Следовательно, число N — размерность матриц—является четным.
Так как  , то обратной каждой из этих матриц будет она сама. Следовательно, равенство (17.13 а) можно переписать в виде
, то обратной каждой из этих матриц будет она сама. Следовательно, равенство (17.13 а) можно переписать в виде
 (17.14 а)
(17.14 а)
Составляя шпуры от обеих сторон последнего равенства, получаем
 (17.146)
(17.146)
Следовательно,

Аналогичный результат справедлив и для других матриц

Ковариантная форма уравнения Дирака
С целью записать уравнение Дирака в ковариантной форме введем новые матрицы

Матрица  эрмитова, а остальные — антиэрмитовы. Сказанное можно компактно записать в следующем виде:
эрмитова, а остальные — антиэрмитовы. Сказанное можно компактно записать в следующем виде:
 (17.16)
(17.16)
Мы будем использовать метрический тензор  определив его равенствами
определив его равенствами

Будем поднимать и опускать индексы матриц у, хотя они и не представляют собой компонент  -вектора,
-вектора,

(подразумевается суммирование по повторяющимся греческим индексам). Правила перестановки (17.12) для матриц у можно записать единым образом

Умножая уравнение (17.2) на  , получаем
, получаем
 (17.19)
(17.19)
Введем «сопряженную по Дираку» волновую функцию  ,
,
 (17.20а)
(17.20а)
и умножим уравнение (17.4) на  Придем к уравнению
Придем к уравнению
 (17.206)
(17.206)
4-вектор тока определяется равенством
 (17.21)
(17.21)
Подействовав теперь на уравнение (17.19) оператором  мы получим
мы получим
 (17.22)
(17.22)
Мы ввели здесь  -импульс
-импульс

При симметризации произведения  был использован тот факт, что операторы дифференцирования коммутируют. Уравнение (17.22) показывает, что релятивистская связь между энергией и импульсом сохраняется.
был использован тот факт, что операторы дифференцирования коммутируют. Уравнение (17.22) показывает, что релятивистская связь между энергией и импульсом сохраняется.
Матрицы Дирака. II
Докажем теперь несколько теорем относительно матриц Дирака. Для исследования этих матриц не обязательно предполагать их эрмитовыми, и мы не будем делать этого. Соотношениями, определяющими их, служат, конечно, правила перестановки (17.18). Любое множество величин, удовлетворяющих условиям  называется алгеброй Клиффорда.
называется алгеброй Клиффорда.
Можно из четырех матриц у образовать новые, составляя произведения каких-либо двух или более из них. Так как квадрат каждой из матриц у равен ±1, имеет смысл рассматривать только произведения, в которых все множители различны. Порядок следования сомножителей несуществен, так как матрицы или коммутируют, или антикоммутируют. Это означает, что существует  различных произведений четырех матриц у. (Число различных комбинаций, которые можно составить из
различных произведений четырех матриц у. (Число различных комбинаций, которые можно составить из  элементов, равно
элементов, равно  ) Добавляя еще единичную матрицу
) Добавляя еще единичную матрицу  получаем перечисленные ниже 16 различных матриц:
получаем перечисленные ниже 16 различных матриц:

Обозначим элементы этого множества через  Можно проверить, что. имеют место следующие свойства (по повторяющимся латинским индексам суммирования нет):
Можно проверить, что. имеют место следующие свойства (по повторяющимся латинским индексам суммирования нет):
 (17.24)
(17.24)
Если  , то всегда существует матрица
, то всегда существует матрица  такая, что
такая, что
 (17.27)
(17.27)
Теорема 1
 (17.28)
(17.28)
Доказательство
Выберем номер k матрицы таким, чтобы для рассматриваемой матрицы Г; можно было воспользоваться свойством (17.27). Используя еще равенство (17.25), получаем

Теорема 2
Сумма

Доказательство
Умножая равенство (17.29) на  , находим
, находим

причем  , так как
, так как  . Возьмем шпур
. Возьмем шпур

согласно теореме 1. Отсюда

Первый важный результат, который дает нам теорема 2, таков: матрицы невозможно представить с помощью матриц, размерность которых меньше четырех, так как из последних нельзя составить 16 линейно независимых матриц, которые мы могли бы использовать в качестве матриц Г. Будем считать отныне, что размерность матриц у равна именно четырем. Подчеркнем следующее — тот факт, что уравнению Дирака можно удовлетворить четырехмерными матрицами, не является следствием четырехмерности пространства — времени.
Из теоремы 2 следует, в частности, что любую четырехмерную матрицу X можно однозначно записать в виде линейной комбинации матриц
 (17.30)
(17.30)
Умножая это равенство на  и находя шпур, получаем
и находя шпур, получаем
 (17.31)
(17.31)
В качестве дальнейшего следствия из теоремы 2 мы можем усилить утверждение, выраженное равенством (17.24). Именно, теперь мы можем сказать, что  , где все матрицы
, где все матрицы  различны при разных индексах
различны при разных индексах  и фиксированных I. Действительно, предположим обратное:
и фиксированных I. Действительно, предположим обратное:
 (17.32 а)
(17.32 а)
Тогда

и

что противоречит свойству линейной независимости матриц  .
.
Теорема 3
Любая матрица X, коммутирующая со всеми матрицами кратна единичной.
Доказательство
Предположим, что матрица X не кратна единичной. Цели матрица X коммутирует со всеми у. то она коммутирует
со всеми матрицами  Используя разложение (17.30), мы можем написать
Используя разложение (17.30), мы можем написать
 (17.33 а)
(17.33 а)
Согласно соотношению (17.27), существует такая матрица  что
что  и, по предположению, X коммутирует с этой
и, по предположению, X коммутирует с этой  . Следовательно,
. Следовательно,
 (17.336)
(17.336)
Поскольку такое разложение является единственным, мы получаем  . Так как матрица
. Так как матрица  была произвольной, с тем исключением, что
была произвольной, с тем исключением, что  мы доказали, что условие
мы доказали, что условие  для всех
для всех  (17.33 в)
(17.33 в)

Теорема 4
Доказанные выше свойства позволяют нам получить другой важный результат, известный как фундаментальная теорема Паули. Эта теорема гласит: если заданы два набора четырехрядных матриц  и
и  и для каждого из них удовлетворяются правила перестановки (17.18), то существует такая несингулярная матрица S, что
и для каждого из них удовлетворяются правила перестановки (17.18), то существует такая несингулярная матрица S, что
 (17.34)
(17.34)
Доказательство
Положим
 (17.35)
(17.35)
где F — произвольная четырехрядная матрица; каждая из матриц  представляет собой одно из 16 произведений, образованных из матрицы
представляет собой одно из 16 произведений, образованных из матрицы  аналогичным
аналогичным
образом построены из  Согласно свойству
Согласно свойству  тогда
тогда  следовательно,
следовательно,

так как матрицы  отмеченные штрихом, построены по тому же образцу, что и нештрихованные матрицы. Тогда для произвольного индекса i мы имеем
отмеченные штрихом, построены по тому же образцу, что и нештрихованные матрицы. Тогда для произвольного индекса i мы имеем

Поскольку  и суммирование
и суммирование  проводится по всем 16 элементам, его можно заменить суммированием по
проводится по всем 16 элементам, его можно заменить суммированием по  что дает, согласно определению (17.35),
что дает, согласно определению (17.35),
 (17.37)
(17.37)
Чтобы показать, что матрица S несингулярна, рассмотрим величину 
 (17.38)
(17.38)
Здесь G — произвольная матрица. По соображениям симметрии
 (17.39 а)
(17.39 а)
для любого I. Учитывая равенство (17.37), можем написать
 (17.396)
(17.396)
Отсюда по теореме 3 следует, что 
Далее,  , так как матрицы F и G, входящие в определения (17.35) и (17.38), можно выбрать произвольно. (Легко показать, использовав в качестве матриц F и G матрицы с единственным отличным от нуля элементом, что равенство
, так как матрицы F и G, входящие в определения (17.35) и (17.38), можно выбрать произвольно. (Легко показать, использовав в качестве матриц F и G матрицы с единственным отличным от нуля элементом, что равенство  для всех таких F и G противоречило бы линейной независимости матриц Г.) Следовательно, матрица S несингулярна и
для всех таких F и G противоречило бы линейной независимости матриц Г.) Следовательно, матрица S несингулярна и
 (17.34)
(17.34)
Более того, матрица S определяется однозначно с точностью до постоянного численного множителя. Действительно, предположим, что  . Тогда
. Тогда  , а это означает, что
, а это означает, что  или
или  . Далее, если по заданным четырем матрицам
. Далее, если по заданным четырем матрицам  удовлетворяющим правилам перестановки (17.18), определить матрицы
удовлетворяющим правилам перестановки (17.18), определить матрицы  очевидно, что новые матрицы также будут удовлетворять соотношениям (17.18).
очевидно, что новые матрицы также будут удовлетворять соотношениям (17.18).
В заключение отметим, что матрица  в (17.23) антикоммутирует с при любом
в (17.23) антикоммутирует с при любом  Нижний нндекс 5 поднимать нельзя.
Нижний нндекс 5 поднимать нельзя.
Явный вид матриц Дирака
Дадим здесь одно из возможных матричных представлений матриц Дирака. Ясно, что соотношения (17.7) и (17.12), или при другом выборе (17.16) и (17.18), не определяют матриц однозначно. Поэтому при решении задач обычно лучше не вводить явных выражений для них.
Мы видели,  матрицы Дирака должны состоять по крайней мере из четырех строк и столбцов. Ограничимся именно такими, четырехрядными матрицами. Ранее мы установили, что шпуры матриц
матрицы Дирака должны состоять по крайней мере из четырех строк и столбцов. Ограничимся именно такими, четырехрядными матрицами. Ранее мы установили, что шпуры матриц  должны равняться нулю. В большинстве задач, включая атомные, рассматриваются частицы, движущиеся с умеренными скоростями. При этом член с
должны равняться нулю. В большинстве задач, включая атомные, рассматриваются частицы, движущиеся с умеренными скоростями. При этом член с  в гамильтониане наиболее велик, и удобно представить
в гамильтониане наиболее велик, и удобно представить  в виде диагональной матрицы. Вместе с условиями
в виде диагональной матрицы. Вместе с условиями  это приводит к выбору
это приводит к выбору

где  — двухрядная единичная матрица.
— двухрядная единичная матрица.
Три матрицы а, для того чтобы ангикоммутировать с  и быть эрмитовыми, должны иметь следующий вид:
и быть эрмитовыми, должны иметь следующий вид:
 (17.406)
(17.406)
где двухрядные матрицы  не обязательно эрмитовы. Они также должны антикоммутнровать друг с другом, и их квадраты должны быть единичными матрицами. Вспомним, что как раз такими свойствами обладают матрицы Паули о. Очевидно, все соотношения (17.12) будут выполняться, если положить
не обязательно эрмитовы. Они также должны антикоммутнровать друг с другом, и их квадраты должны быть единичными матрицами. Вспомним, что как раз такими свойствами обладают матрицы Паули о. Очевидно, все соотношения (17.12) будут выполняться, если положить

и принять определение (17.40 а). Тогда, согласно (17.15) и (17.23), получим

Мы увидим, что выбор матриц Дирака в виде (17.40 а) и (17.40 в) удобен при обсуждении вопросов, связанных со спином. В предельном релятивистском случае обычно удобнее диагонализовать матрицу  Конечно, все физические следствия не должны зависеть от выбора представления.
Конечно, все физические следствия не должны зависеть от выбора представления.
Релятивистская инвариантность уравнения Дирака
Прежде чем решать уравнение Дирака и извлекать из него физические следствия, мы покажем, что физические результаты не зависят от выбора лоренцовой системы отсчета, использованной при их выводе. Если уравнение Дирака решено в двух различных системах, то решения должны описывать одно и то же физическое состояние. Это не означает, что компоненты  не меняются при преобразовании Лоренца. Ситуация здесь аналогична положению с тензором электромагнитного поля, когда компоненты напряженностей
не меняются при преобразовании Лоренца. Ситуация здесь аналогична положению с тензором электромагнитного поля, когда компоненты напряженностей  и
и  преобразуются, но форма уравнений Максвелла остается инвариантной. Так и здесь мы увидим, что величины
преобразуются, но форма уравнений Максвелла остается инвариантной. Так и здесь мы увидим, что величины  преобразуются, но форма уравнения Дирака остается неизменной.
преобразуются, но форма уравнения Дирака остается неизменной.
Наиболее общее однородное (т. е. не включающее пространственно-временных трансляций) преобразование
Лоренца можно записать следующим образом:
 (17.41 а)
(17.41 а)
где

Равенство (17.41 б) вытекает из условия инвариантности вещественной квадратичной формы 
В частном случае стандартного преобразования Лоренца (движение двух координатных систем вдоль их общей оси  с относительной скоростью V, причем начала координат совпадают в момент времени
с относительной скоростью V, причем начала координат совпадают в момент времени  ) величины
) величины  имеют вид
имеют вид

Используя соотношение

вытекающее из уравнения (17.41 а), и замечая, что градиент  представляет собой ковариантный вектор, из уравнения (17.19) можно получить
представляет собой ковариантный вектор, из уравнения (17.19) можно получить
 (17.43)
(17.43)
Введем величины  . С помощью уравнения (17.416) можно проверить, что они удовлетворяют соотношениям (17.18). Поэтому на основании фундаментальной теоремы Паули существует (определяемая однозначно с точностью до постоянного множителя) такая матрица S, что
. С помощью уравнения (17.416) можно проверить, что они удовлетворяют соотношениям (17.18). Поэтому на основании фундаментальной теоремы Паули существует (определяемая однозначно с точностью до постоянного множителя) такая матрица S, что
 (17.44)
(17.44)
Подставив эту величину в уравнение (17.43) и помножив все слева на  , получим
, получим
 (17.45)
(17.45)
Определим величину
 (17.46)
(17.46)
Тогда вместо уравнения (17.43) можем написать
 (17.47)
(17.47)
Это уравнение имеет в точности такой же вид, что и (17.19). Как мы и предсказывали выше, волновые функции  преобразуются, но матрицы
преобразуются, но матрицы  остаются теми же самыми. Поэтому если мы сможем доказать, что величина
остаются теми же самыми. Поэтому если мы сможем доказать, что величина  имеет тот же физический смысл в штрихованной системе координат, что и
имеет тот же физический смысл в штрихованной системе координат, что и  в нештрихованной, то мы полностью продемонстрируем ковариантность теории. Для этой цели установим еще некоторые свойства матрицы
в нештрихованной, то мы полностью продемонстрируем ковариантность теории. Для этой цели установим еще некоторые свойства матрицы  .
.
Из соотношений эрмитовости (17.16) и равенств (17.416), (17.44) находим
 (17.48 а)
(17.48 а)
Подставляя сюда  вместо получаем
вместо получаем
 (17.49 а)
(17.49 а)
Согласно (17.33), это дает
 (17.50 б)
(17.50 б)
Взяв равенство, эрмитово-сопряженное с (17.50 б), можем убедиться, что константа b вещественна. Наложим на 5 условие нормировки  Тогда из равенства
Тогда из равенства
(17.50б) следует, что  и, так как b — вещественная величина, мы получаем
и, так как b — вещественная величина, мы получаем
 (17.51)
(17.51)
Чтобы выяснить физический смысл этого результата, рассмотрим величину 
 (17.52)
(17.52)
Здесь были использованы равенства (17.44) и (17.50). Так как собственные значения  положительно определены, то, взяв шпур от равенства (17.52), получим
положительно определены, то, взяв шпур от равенства (17.52), получим

т. е.
 (17.53)
(17.53)
Первый случай,  соответствует преобразованию с инверсией времени.
соответствует преобразованию с инверсией времени.
Рассмотрим теперь трансформационные свойства сопряженной функции 
 (17.46)
(17.46)
Теперь мы в состоянии ответить на поставленный выше вопрос, описывает ли функция  такую же физическую ситуацию в штрихованной системе, какую описывает волновая функция
такую же физическую ситуацию в штрихованной системе, какую описывает волновая функция  в нештрихованной системе? Ответ будет положительным, если величина
в нештрихованной системе? Ответ будет положительным, если величина  дает плотность вероятности в штрихованной системе,
дает плотность вероятности в штрихованной системе,
Рассмотрим плотность тока
 (17-56)
(17-56)
Следовательно, относительно преобразований Лоренца, не включающих инверсии времени, величина  преобразуется как 4-вектор, что дает нужный закон преобразования величины При общих преобразованиях Лоренца
преобразуется как 4-вектор, что дает нужный закон преобразования величины При общих преобразованиях Лоренца  ведет себя как псевдовектор.
ведет себя как псевдовектор.
Явный вид матрицы преобразования
Выпишем, наконец, в явном виде матрицу S, соответствующую собственному непрерывному преобразованию Лоренца,  Достаточно рассмотреть только бесконечно малые преобразования, так как любое конечное преобразование можно представить как результат повторного применения бесконечно малых. Для последних
Достаточно рассмотреть только бесконечно малые преобразования, так как любое конечное преобразование можно представить как результат повторного применения бесконечно малых. Для последних
 (17.57)
(17.57)
Здесь  — малый параметр; в дальнейшем будут удерживаться только линейные по
— малый параметр; в дальнейшем будут удерживаться только линейные по  члены.
члены.
Согласно (17.41б),
 (17.58)
(17.58)
Далее действуем следующим образом:
 (17.59)
(17.59)
Отсюда
 (17.61)
(17.61)
Матрица Т определена однозначно с точностью до слагаемого, кратного единичной матрице. Действительно, если бы существовали две такие матрицы Т, то, согласно (17.61), их разность коммутировала бы со всеми матрицами у. Это возможно лишь для матрицы, кратной единичной. Условие нормировки устраняет и эту неопределенность, так как

Легко убедиться, что матрица
 (17.63)
(17.63)
удовлетворяет условиям (17.61) и (17.62). Следовательно, Т и есть искомая матрица преобразования; как видно, она антисимметрична.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Часть I. ТЕОРИЯ СТРОЕНИЯ АТОМА
- 1. УРАВНЕНИЕ ШРЕДИНГЕРА И ПРИБЛИЖЕННЫЕ МЕТОДЫ ЕГО РЕШЕНИЯ
- 2. ИНТЕГРАЛЫ ДВИЖЕНИЯ
- 3. ТОЖДЕСТВЕННОСТЬ ЧАСТИЦ И СИММЕТРИЯ
- 4. ДВУХЭЛЕКТРОННЫЕ АТОМЫ. РАСЧЕТ ПО ТЕОРИИ ВОЗМУЩЕНИЙ
- 5. ДВУХЭЛЕКТРОННЫЕ АТОМЫ. РАСЧЕТ ВАРИАЦИОННЫМ МЕТОДОМ
- 6. САМОСОГЛАСОВАННОЕ ПОЛЕ
- 7. СТАТИСТИЧЕСКАЯ МОДЕЛЬ ТОМАСА—ФЕРМИ
- 8. ТЕОРИЯ МУЛЬТИПЛЕТОВ. СЛОЖЕНИЕ МОМЕНТОВ
- 9. ТЕОРИЯ МУЛЬТИПЛЕТОВ. ЭЛЕКТРОСТАТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ
- 10. ТЕОРИЯ МУЛЬТИПЛЕТОВ. МАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ
- 11. МОЛЕКУЛЫ
- 12. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ ИЗЛУЧЕНИЯ
- 13. ИНТЕНСИВНОСТЬ ИЗЛУЧЕНИЯ
- 14. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
- 15. СТОЛКНОВЕНИЯ АТОМОВ С ЗАРЯЖЕННЫМИ ЧАСТИЦАМИ
- Часть II. РЕЛЯТИВИСТСКИЕ ТЕОРИИ
- 16. УРАВНЕНИЕ КЛЕЙНА—ГОРДОНА
- 17. УРАВНЕНИЕ ДИРАКА. ФОРМАЛЬНАЯ ТЕОРИЯ
- 18. РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА
- Часть III. ВВЕДЕНИЕ В ТЕОРИЮ ПОЛЯ
- 19. КВАНТОВАНИЕ ПОЛЯ
- 20. ВТОРИЧНОЕ КВАНТОВАНИЕ НЕСКОЛЬКИХ ПОЛЕЙ ЧАСТИЦ
- 21. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ. КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- ЛИТЕРАТУРА