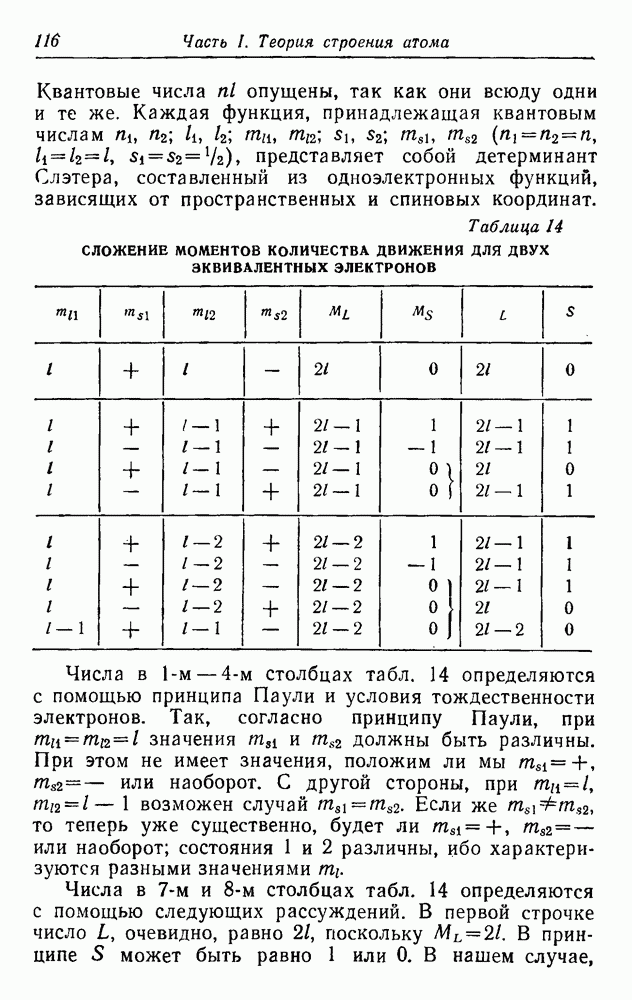
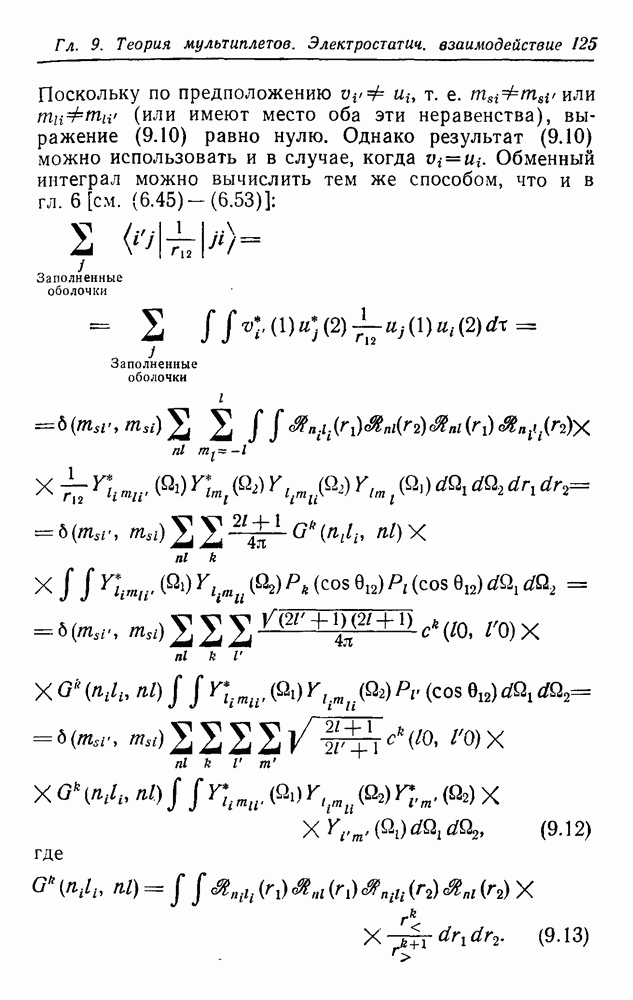| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7. СТАТИСТИЧЕСКАЯ МОДЕЛЬ ТОМАСА—ФЕРМИ
В предыдущей главе рассматривалась задача о вычислении уровней энергии и волновых функций атомов по методу самосогласованного поля. Как мы видели, все численные расчеты оказываются при этом весьма громоздкими, особенно в случае многоэлектронных атомов. Для последних существует, однако, более простой и достаточно надежный приближенный способ. Он разработан Томасом [15] и Ферми [16] и основан на статистике Ферми—Дирака. Результаты, которые получаются таким путем, менее точны, чем при вычислениях по методу Хартри—Фока. Тем не менее метод Томаса—Ферми очень полезен для расчета формфакторов или эффективных потенциалов, которые затем можно использовать в качестве исходных пробных потенциалов в методе самосогласованного поля. Он применяется также при изучении движения нуклонов в ядрах и электронов в металлах.
Цель статистического метода Томаса—Ферми состоит в вычислении эффективной потенциальной энергии бесконечно малого пробного заряда и отыскании электронной плотности  около атома. В дальнейшем будут использоваться обычные единицы.
около атома. В дальнейшем будут использоваться обычные единицы.
Рассмотрим систему электронов, движущихся в объеме  в поле со сферически симметричным потенциалом
в поле со сферически симметричным потенциалом  Будем считать, что потенциал достаточно слабо меняется с расстоянием
Будем считать, что потенциал достаточно слабо меняется с расстоянием  , так что к системе можно применять статистику Ферми—Дирака для свободных частиц. Допустим далее, что взаимодействие между электронами достаточно для установления статистического равновесия, но в то же время настолько мало, что можно говорить о кинетической и потенциальной энергии каждого отдельного электрона. Пусть, наконец,
, так что к системе можно применять статистику Ферми—Дирака для свободных частиц. Допустим далее, что взаимодействие между электронами достаточно для установления статистического равновесия, но в то же время настолько мало, что можно говорить о кинетической и потенциальной энергии каждого отдельного электрона. Пусть, наконец,
конец,  . Функция распределения имеет вид
. Функция распределения имеет вид

где  — химический потенциал. Если положить
— химический потенциал. Если положить  , то
, то

Но,
Следовательно, при абсолютном нуле  совпадает с наибольшей энергией электронов. В силу принципа Паули, электроны заполняют все состояния, начиная с основного вплоть до состояний с энергией
совпадает с наибольшей энергией электронов. В силу принципа Паули, электроны заполняют все состояния, начиная с основного вплоть до состояний с энергией  . Ясно, что
. Ясно, что  не может зависеть от
не может зависеть от  . В противном случае электроны переходили бы в области пространства с наименьшими
. В противном случае электроны переходили бы в области пространства с наименьшими  , поскольку это уменьшало бы полную энергию системы, и этот процесс продолжался бы, пока значения
, поскольку это уменьшало бы полную энергию системы, и этот процесс продолжался бы, пока значения  не выровнялись бы. Очевидно,
не выровнялись бы. Очевидно,

где  — максимальный импульс электронов (так называемый импульс Ферми). Он должен зависеть от
— максимальный импульс электронов (так называемый импульс Ферми). Он должен зависеть от  , чтобы химический потенциал
, чтобы химический потенциал  был постоянен.
был постоянен.
Легко получить выражение, связывающее  с
с  . Для этой цели вычислим число квантовых состояний поступательного движения полностью свободного электрона, которым отвечают абсолютные значения импульса в интервале от
. Для этой цели вычислим число квантовых состояний поступательного движения полностью свободного электрона, которым отвечают абсолютные значения импульса в интервале от  до
до  . Пусть электрон движется в ящике объемом Q в отсутствие каких-либо сил. Искомое число квантовых состояний равно (см. [1])
. Пусть электрон движется в ящике объемом Q в отсутствие каких-либо сил. Искомое число квантовых состояний равно (см. [1])

где  , а множитель 2 учитывает две возможные ориентации спина электрона. Интегрируя выражение (7.4) от 0 до
, а множитель 2 учитывает две возможные ориентации спина электрона. Интегрируя выражение (7.4) от 0 до  и приравнивая результат полному числу электронов N, получаем
и приравнивая результат полному числу электронов N, получаем

Предположим теперь, что внутри исходного большого объема  можно выделить ящик объемом Q, достаточно большой, чтобы выполнялось равенство (7.5), и в то же время достаточно малый, чтобы внутри него потенциальная энергия менялась не слишком сильно. Тогда можно считать, что соотношения (7.5) и (7.3) выполняются одновременно. Произведем теперь калибровочное преобразование потенциальной энергии
можно выделить ящик объемом Q, достаточно большой, чтобы выполнялось равенство (7.5), и в то же время достаточно малый, чтобы внутри него потенциальная энергия менялась не слишком сильно. Тогда можно считать, что соотношения (7.5) и (7.3) выполняются одновременно. Произведем теперь калибровочное преобразование потенциальной энергии
 (7.6)
(7.6)
Тогда из формул (7.3) и (7.5) следует, что

Уравнение Пуассона связывает электростатический потенциал—  с плотностью заряда —
с плотностью заряда —  . Легко привести это уравнение к виду
. Легко привести это уравнение к виду

Подставляя сюда выражение (7.7), получаем

При  главным членом в V должна быть кулоновская потенциальная энергия электрона в поле ядра
главным членом в V должна быть кулоновская потенциальная энергия электрона в поле ядра  . Поэтому решение уравнения (7.9) должно удовлетворять граничному условию
. Поэтому решение уравнения (7.9) должно удовлетворять граничному условию

Произведем замену переменных

где  — первый боровский радиус. Следовательно, уравнение, которое надо решить, имеет вид
— первый боровский радиус. Следовательно, уравнение, которое надо решить, имеет вид

а граничное условие есть  .
.
Решения уравнения Томаса — Ферми
Уравнение (7.12) есть нелинейное дифференциальное уравнение второго порядка. Важно отметить, что оно не зависит от Z. Очевидно, мы получим целое семейство решений, ибо пока задано только одно граничное условие. Различные решения можно характеризовать значением первой производной в нуле, которое может выбираться произвольно. В работе [17] было выполнено численное интегрирование при различных значениях первой производной в нуле. Оказалось, что решение можно представить в виде полусходящегося ряда

где

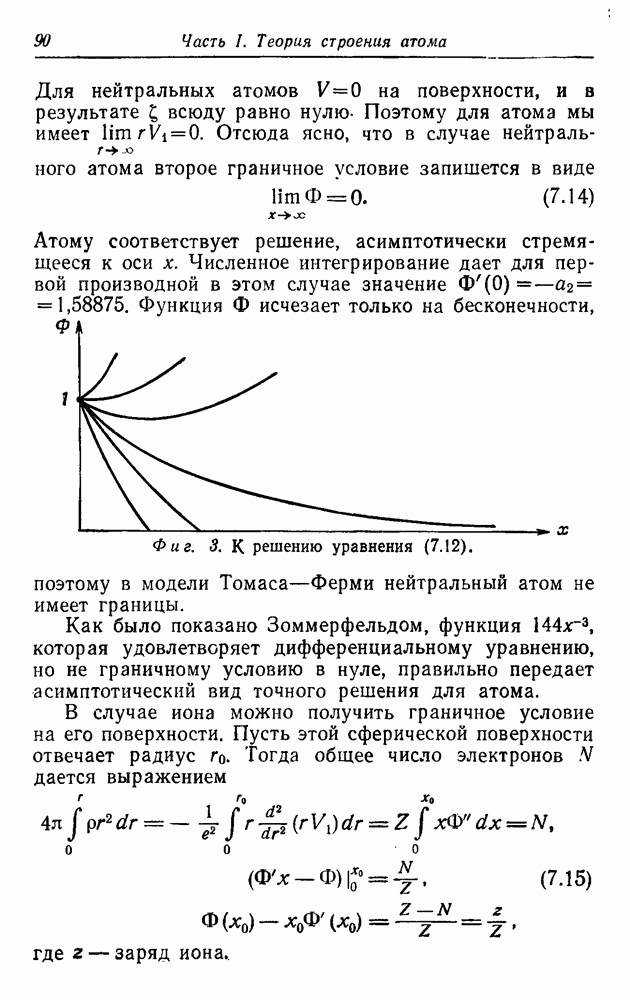
Легко видеть, что все кривые, соответствующие решениям уравнения (7.12), вблизи нуля вогнуты (так как  ). Следовательно, если некоторое решение нигде не обращается в нуль, то его график остается вогнутым и оно будет либо расходиться при больших значениях
). Следовательно, если некоторое решение нигде не обращается в нуль, то его график остается вогнутым и оно будет либо расходиться при больших значениях  либо асимптотически стремиться к оси
либо асимптотически стремиться к оси  . Если решение обращается в нуль в конечной точке
. Если решение обращается в нуль в конечной точке  , то дифференциальное уравнение перестает быть справедливым. Действительно, физически ясно, что уравнение (7.12) может годиться только для положительных значений Ф, для отрицательных Ф электронная плотность должна быть нулем, так как нет занятых состояний с
, то дифференциальное уравнение перестает быть справедливым. Действительно, физически ясно, что уравнение (7.12) может годиться только для положительных значений Ф, для отрицательных Ф электронная плотность должна быть нулем, так как нет занятых состояний с  [см. (7.2), а также (7.7)]. Поэтому корректное дифференциальное уравнение для отрицательных Ф имеет вид
[см. (7.2), а также (7.7)]. Поэтому корректное дифференциальное уравнение для отрицательных Ф имеет вид  . Решением его
. Решением его  , где А — константа, которая в силу непрерывности равна
, где А — константа, которая в силу непрерывности равна  . Таким образом, решение полностью определено, если оно известно для
. Таким образом, решение полностью определено, если оно известно для  и мы ограничимся только этой областью значений. Поведение различных решений представлено на фиг. 3.
и мы ограничимся только этой областью значений. Поведение различных решений представлено на фиг. 3.
Для нейтральных свободных атомов (т. е. атомов, не подвергающихся внешнему давлению) легко указать второе граничное условие и, следовательно, найти единственное решение. Действительно, на поверхности свободного атома (или иона) должно быть  .
.
Для нейтральных атомов  на поверхности, и в результате
на поверхности, и в результате  всюду равно нулю. Поэтому для атома мы имеет
всюду равно нулю. Поэтому для атома мы имеет  . Отсюда ясно, что в случае нейтрального атома второе граничное условие запишется в виде
. Отсюда ясно, что в случае нейтрального атома второе граничное условие запишется в виде

Атому соответствует решение, асимптотически стремящееся к оси  Численное интегрирование дает для первой производной в этом случае значение
Численное интегрирование дает для первой производной в этом случае значение  . Функция Ф исчезает только на бесконечности, поэтому в модели Томаса—Ферми нейтральный атом не имеет границы.
. Функция Ф исчезает только на бесконечности, поэтому в модели Томаса—Ферми нейтральный атом не имеет границы.

Фиг. 3. К решению уравнения (7.12).
Как было показано Зоммерфельдом, функция  , которая удовлетворяет дифференциальному уравнению, но не граничному условию в нуле, правильно передает асимптотический вид точного решения для атома.
, которая удовлетворяет дифференциальному уравнению, но не граничному условию в нуле, правильно передает асимптотический вид точного решения для атома.
В случае иона можно получить граничное условие на его поверхности. Пусть этой сферической поверхности отвечает радиус  . Тогда общее число электронов N дается выражением
. Тогда общее число электронов N дается выражением

где  — заряд иона.
— заряд иона.
Для свободного иона  при
при  откуда вытекает, что
откуда вытекает, что

Следовательно, решения уравнения (7.12), которые обращаются в нуль при конечных значениях  соответствуют ионам радиуса
соответствуют ионам радиуса  Так как наклон Ф в точке
Так как наклон Ф в точке  должен быть отрицательным (см. фиг. 3), из равенств (7.16) следует, что теория не описывает свободные отрицательные ионы.
должен быть отрицательным (см. фиг. 3), из равенств (7.16) следует, что теория не описывает свободные отрицательные ионы.
В случае нейтральных атомов условия (7.16) дают

Отсюда видно, что не существует решения с конечным радиусом  . Однако для асимптотического решения Зоммерфельда
. Однако для асимптотического решения Зоммерфельда  и в пределе при
и в пределе при  как Ф, так и
как Ф, так и  обращаются в нуль.
обращаются в нуль.
Если атом находится под давлением  то плотность
то плотность  более не равна нулю. Решения, которые не обращаются в нуль при конечных значениях
более не равна нулю. Решения, которые не обращаются в нуль при конечных значениях  соответствуют этому случаю. Уравнение (7.15) определяет значение
соответствуют этому случаю. Уравнение (7.15) определяет значение  и, следовательно, радиус таких систем. Поскольку атомы нейтральны,
и, следовательно, радиус таких систем. Поскольку атомы нейтральны,

что определяет точку  в которой касательная к функции Ф проходит через начало координат. Для
в которой касательная к функции Ф проходит через начало координат. Для  дифференциальное уравнение (7.12) не имеет физического смысла.
дифференциальное уравнение (7.12) не имеет физического смысла.
Применения
Все атомы в модели Томаса — Ферми имеют одинаковое распределение электронов, исключая различие в масштабе длины и в полном числе электронов. Формулы
(7.11) показывают, что масштаб длины для любого атома пропорционален  . Таким образом, полный радиус атома уменьшается как
. Таким образом, полный радиус атома уменьшается как  . С другой стороны, можно показать, что радиус сферы, содержащий все электроны, кроме одного, приближенно пропорционален
. С другой стороны, можно показать, что радиус сферы, содержащий все электроны, кроме одного, приближенно пропорционален  .
.
Ферми воспользовался изложенным методом для решения интересной задачи о том, при какой величине заряда ядра Z впервые появляется состояние с данным моментом количества движения. Рассмотрим приведенное уравнение для радиальной функции

[Мы воспользовались здесь обычной в квазиклассическом методе заменой  на
на  ] Связанные состояния существуют, лишь если
] Связанные состояния существуют, лишь если  в некоторой области значений
в некоторой области значений  . Поскольку
. Поскольку  , это означает, что должны выполняться условия
, это означает, что должны выполняться условия

для некоторой области г.
Из таблиц работы [17] явствует, что функция  имеет пологий максимум:
имеет пологий максимум:

Для выполнения неравенства (7.19) необходимо, чтобы

Эта формула определяет величину заряда ядра Z, начиная с которой электрон с данным моментом количества движения  оказывается связанным. По-видимому, знак «больше» в неравенстве (7.20) можно заменить на «равно», если несколько увеличить коэффициент. Приняв его равным 0,17 вместо 0,157, т. е. положив
оказывается связанным. По-видимому, знак «больше» в неравенстве (7.20) можно заменить на «равно», если несколько увеличить коэффициент. Приняв его равным 0,17 вместо 0,157, т. е. положив

мы получим

Округляя до ближайшего целого числа, будем иметь 5, 21, 58, 124. Сравнивая с опытом, видим, что первые три значения правильны. Согласно последнему результату,  -электроны могут появиться только у 124-го элемента. Это на шесть номеров дальше предсказываемого теоретически инертного газа с зарядом ядра
-электроны могут появиться только у 124-го элемента. Это на шесть номеров дальше предсказываемого теоретически инертного газа с зарядом ядра  для наиболее тяжелого элемента, открытого к настоящему времени,
для наиболее тяжелого элемента, открытого к настоящему времени, 
Выше было показано, что функция  имеет очень пологий максимум. Можно ожидать поэтому, что для наибольшего значения
имеет очень пологий максимум. Можно ожидать поэтому, что для наибольшего значения  , которое еще может соответствовать связанному состоянию в данном атоме, потенциал
, которое еще может соответствовать связанному состоянию в данном атоме, потенциал  будет почти точно компенсирован центробежной энергией. В таких условиях небольшое изменение в величине заряда ядра Z привело бы к большому изменению волновой функции. Именно этот эффект и был обнаружен Хартри для
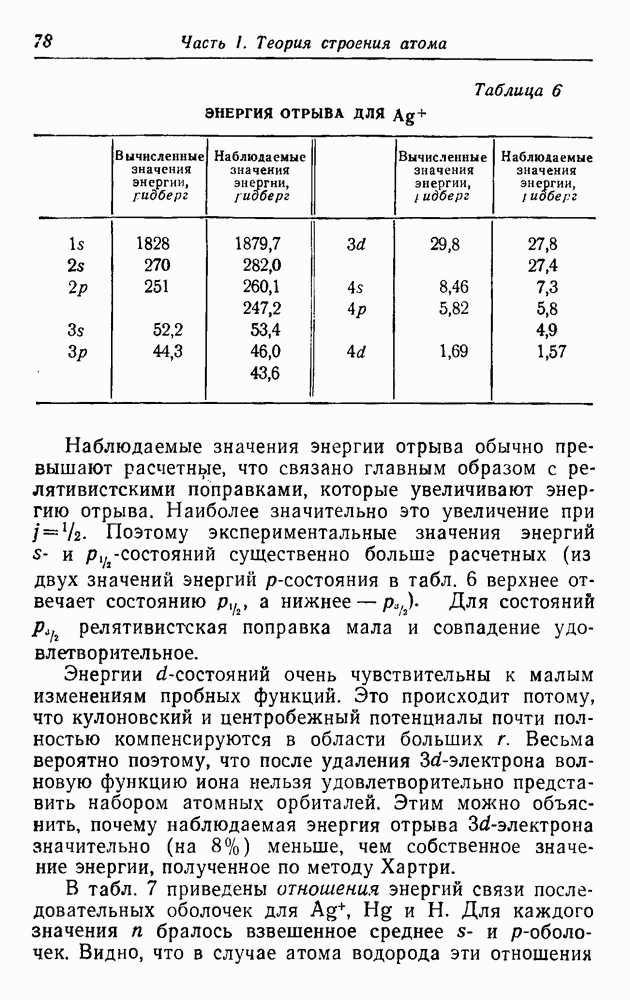
будет почти точно компенсирован центробежной энергией. В таких условиях небольшое изменение в величине заряда ядра Z привело бы к большому изменению волновой функции. Именно этот эффект и был обнаружен Хартри для  -электронов (см. стр. 78).
-электронов (см. стр. 78).
Поправка на обменное взаимодействие. Уравнение Томаса — Ферми — Дирака
Уравнение Томаса—Ферми (7.12) не учитывает обменного взаимодействия. Учет последнего был произведен
Дираком [18]. Дадим здесь простой вывод этой поправки.
Как мы знаем, в методе Хартри — Фока обменный член имеет вид

В духе метода Томаса—Ферми будем считать электроны свободными (потенциальная энергия постоянна). Таким образом, полагаем

Тогда

Тем самым подтверждается формула (6.55). Очевидно,

Напомним, что для i-го электрона

Следовательно,

Вычисление этого интеграла дает [3]

где

 ; при изменении
; при изменении  от нуля до единицы F монотонно уменьшается от 1 до
от нуля до единицы F монотонно уменьшается от 1 до 
Формула (7.26) определяет эффективный обменный потенциал для  электрона. Усредним ее по всем электронам
электрона. Усредним ее по всем электронам

Подставляя сюда значение  из формулы (7.25), находим
из формулы (7.25), находим

Это выражение можно рассматривать как электростатическую собственную энергию «дырки» в распределении
заряда  . Подставляя выражение для
. Подставляя выражение для  из формулы (7.23), можно вычислить интеграл явно
из формулы (7.23), можно вычислить интеграл явно

Теперь надо найти связь между электростатической потенциальной энергией V и плотностью р. Наиболее простое соображение состоит в том, что максимальная энергия электрона дается теперь вместо (7.3) формулой

Здесь к потенциалу  прибавлена эффективная обменная потенциальная энергия
прибавлена эффективная обменная потенциальная энергия  . Эта энергия зависит от импульса в соответствии с (7.26). В рассматриваемом случае электрона с максимальной энергией параметр
. Эта энергия зависит от импульса в соответствии с (7.26). В рассматриваемом случае электрона с максимальной энергией параметр  согласно формуле
согласно формуле  Результат (7.31) совпадает с полученной ниже формулой (7.34).
Результат (7.31) совпадает с полученной ниже формулой (7.34).
Для разнообразия получим равенство (7.31) другим способом. Рассмотрим для этого полную энергию системы электронов, проварьируем ее как функцию плотности  и получим искомую связь из условия стационарности Е. Такой подход предложен Ленцем [19]. То же самое можно было бы сделать и при выводе уравнения Томаса — Ферми.
и получим искомую связь из условия стационарности Е. Такой подход предложен Ленцем [19]. То же самое можно было бы сделать и при выводе уравнения Томаса — Ферми.
Полная энергия есть сумма кинетической  и потенциальной
и потенциальной  энергий. Полную кинетическую энергию электронов можно найти, умножая число состояний (7.4) на
энергий. Полную кинетическую энергию электронов можно найти, умножая число состояний (7.4) на  и интегрируя результат по всем импульсам от 0 до
и интегрируя результат по всем импульсам от 0 до  и по всему объему системы. Таким путем легко находим
и по всему объему системы. Таким путем легко находим

Потенциальная энергия равна

Первый член здесь обусловлен взаимодействием электронов с зарядом ядра, второй — электрон-электронным взаимодействием. Множитель  введен, чтобы не учитывать дважды каждую пару электронов. Третий член есть обменная энергия (усредненная величина
введен, чтобы не учитывать дважды каждую пару электронов. Третий член есть обменная энергия (усредненная величина  ) с множителем
) с множителем  введенным из тех же соображений. Приравнивая нулю произвольную вариацию Е по
введенным из тех же соображений. Приравнивая нулю произвольную вариацию Е по  , получаем
, получаем

Строго говоря, вариация Е не является совершенно произвольной, так как должно выполняться условие  , где N — полное число электронов. Это дополнительное условие можно учесть методом неопределенных множителей Лагранжа, что добавит в левую часть (7.34) член К, где А, — неопределенный множитель. Далее можно произвести калибровочное преобразование
, где N — полное число электронов. Это дополнительное условие можно учесть методом неопределенных множителей Лагранжа, что добавит в левую часть (7.34) член К, где А, — неопределенный множитель. Далее можно произвести калибровочное преобразование  в результате чего вновь получается формула (7.34)
в результате чего вновь получается формула (7.34)
Использование средней эффективной обменной энергии (7.30) в выражении для потенциальной энергии (7.33) оправдано. Здесь мы имеем дело с полной обменной энергией всех электронов. В методе Хартри—Фока, где мы рассматривали отдельные электроны, использование средней эффективной обменной энергии (7.30) вместо обменного потенциала представляло собой лишь приближение.
Разрешим теперь уравнение (7.34) относительно плотности. Полагая  имеем
имеем

Перед корнем выбран знак «плюс», дабы обеспечить согласие с методом Томаса—Ферми и избежать отрицательной плотности. Полагая

получаем

Уравнение Пуассона дает

Окончательно, производя замену переменных

получаем

Зто есть уравнение Томаса—Ферми—Дирака. В отличие от уравнения (7.12) оно зависит от заряда ядра Z через параметр  . Видно, что при
. Видно, что при  уравнение (7.39) переходит в (7.12).
уравнение (7.39) переходит в (7.12).
Граничные условия к уравнению (7.39) имеют вид

Здесь уже нельзя определить границу свободных атомов и ионов условием  , так как, согласно (7.37),
, так как, согласно (7.37),  нигде не обращается в нуль. Мы можем, однако, определить значение
нигде не обращается в нуль. Мы можем, однако, определить значение  из условия обращения в нуль давления на границе. Найдем для этого, исходя из формул (7.32) и (7.33), удельную энергию (энергию, приходящуюся на одну частицу). Фактически имеется некоторая трудность, связанная с электростатическим
из условия обращения в нуль давления на границе. Найдем для этого, исходя из формул (7.32) и (7.33), удельную энергию (энергию, приходящуюся на одну частицу). Фактически имеется некоторая трудность, связанная с электростатическим
взаимодействием между электронами, однако формула 

правильна.
Давление Р дается формулой  , где у — удельный объем, a S - энтропия. Поскольку результат (7.41) получен для
, где у — удельный объем, a S - энтропия. Поскольку результат (7.41) получен для  , когда энтропия равна нулю и, следовательно, постоянна, надо просто продифференцировать выражение (7.41) по v. Вспоминая, что
, когда энтропия равна нулю и, следовательно, постоянна, надо просто продифференцировать выражение (7.41) по v. Вспоминая, что  , получаем
, получаем

Давление обращается в нуль при

т. е.

В пренебрежении обменным взаимодействием давление Р обратилось бы в нуль при  отсюда следовало бы, что
отсюда следовало бы, что  в согласии с прежним результатом. Плотность, меньшая чем (7.43), не имеет физического смысла в модели Томаса—Ферми—Дирака, поскольку она соответствовала бы отрицательному давлению. Подставляя выражение (7.43) в (7.37), находим после некоторых преобразований
в согласии с прежним результатом. Плотность, меньшая чем (7.43), не имеет физического смысла в модели Томаса—Ферми—Дирака, поскольку она соответствовала бы отрицательному давлению. Подставляя выражение (7.43) в (7.37), находим после некоторых преобразований

Итак, в теории Томаса—Ферми—Дирака атомы, равно как ионы, имеют конечный радиус. Уравнение (7.44) неприменимо, конечно, к атомам, находящимся под внешним давлением, так как в этом случае плотность может превышать значение (7.43). [Как можно усмотреть из уравнения (7.39), не существует решений, которые стремились бы к нулю при  Это обстоятельство не вызывает затруднений, так как решения уравнения для атомов не удовлетворяют больше условию
Это обстоятельство не вызывает затруднений, так как решения уравнения для атомов не удовлетворяют больше условию
(7.14).] Как и раньше, дифференциальное уравнение применимо лишь при 
Численные расчеты были выполнены в работе [17] и др. Выяснилось, что модель Томаса—Ферми—Дирака не описывает свободных отрицательно заряженных ионов.
Модель Ферми полезна при вычислении характеристик, которые зависят от поведения системы электронов в среднем. К числу их относятся форм-фактор, полная энергия всех электронов, электростатический потенциал, создаваемый всеми электронами в месте расположения ядра, средний потенциал возбуждения. Последний встречается при вычислении тормозной способности атома и определяется равенством

здесь  — средний потенциал возбуждения
— средний потенциал возбуждения  состояния. Метод Томаса—Ферми, даже с учетом обменного взаимодействия, мало пригоден для вычисления характеристик, зависящих от поведения внешних электронов, таких, как потенциал ионизации или средний квадрат радиуса атома (последняя величина важна в теории диамагнетизма). Ко всем таким расчетам следует относиться с осторожностью.
состояния. Метод Томаса—Ферми, даже с учетом обменного взаимодействия, мало пригоден для вычисления характеристик, зависящих от поведения внешних электронов, таких, как потенциал ионизации или средний квадрат радиуса атома (последняя величина важна в теории диамагнетизма). Ко всем таким расчетам следует относиться с осторожностью.
Обобщение теории на случай ненулевых температур было дано в работе [20]. Далее, в работе [21] для ряда атомов было решено радиальное одноэлектронное уравнение Шредингера для всех состояний  заполненных в нормальных условиях. Для потенциала
заполненных в нормальных условиях. Для потенциала  было использовано выражение, полученное по методу Томаса—Ферми—Дирака. Это дает как уровни энергии, так и соответствующие им волновые функции. С помощью последних можно затем вычислить потенциал по формулам метода Хартри—Фока. Это дало бы очень хорошие исходные выражения для расчета уровней методом Хартри—Фока. Для тех атомов, для которых расчет по методу самосогласованного поля еще не выполнен, волновые функции, полученные в работе [21], являются наилучшими из всех известных. То, что они действительно
было использовано выражение, полученное по методу Томаса—Ферми—Дирака. Это дает как уровни энергии, так и соответствующие им волновые функции. С помощью последних можно затем вычислить потенциал по формулам метода Хартри—Фока. Это дало бы очень хорошие исходные выражения для расчета уровней методом Хартри—Фока. Для тех атомов, для которых расчет по методу самосогласованного поля еще не выполнен, волновые функции, полученные в работе [21], являются наилучшими из всех известных. То, что они действительно
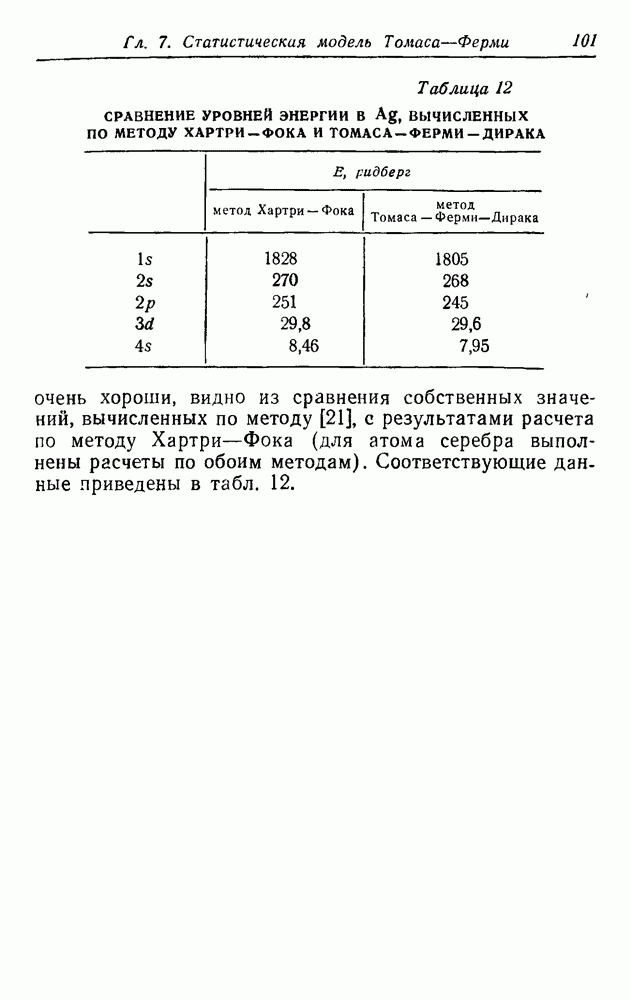
Таблица 12. СРАВНЕНИЕ УРОВНЕЙ ЭНЕРГИИ В Ag, ВЫЧИСЛЕННЫХ ПО МЕТОДУ ХАРТРИ—ФОКА И ТОМАСА—ФЕРМИ—ДИРАКА

очень хороши, видно из сравнения собственных значений, вычисленных по методу [21], с результатами расчета по методу Хартри—Фока (для атома серебра выполнены расчеты по обоим методам). Соответствующие данные приведены в табл. 12.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Часть I. ТЕОРИЯ СТРОЕНИЯ АТОМА
- 1. УРАВНЕНИЕ ШРЕДИНГЕРА И ПРИБЛИЖЕННЫЕ МЕТОДЫ ЕГО РЕШЕНИЯ
- 2. ИНТЕГРАЛЫ ДВИЖЕНИЯ
- 3. ТОЖДЕСТВЕННОСТЬ ЧАСТИЦ И СИММЕТРИЯ
- 4. ДВУХЭЛЕКТРОННЫЕ АТОМЫ. РАСЧЕТ ПО ТЕОРИИ ВОЗМУЩЕНИЙ
- 5. ДВУХЭЛЕКТРОННЫЕ АТОМЫ. РАСЧЕТ ВАРИАЦИОННЫМ МЕТОДОМ
- 6. САМОСОГЛАСОВАННОЕ ПОЛЕ
- 7. СТАТИСТИЧЕСКАЯ МОДЕЛЬ ТОМАСА—ФЕРМИ
- 8. ТЕОРИЯ МУЛЬТИПЛЕТОВ. СЛОЖЕНИЕ МОМЕНТОВ
- 9. ТЕОРИЯ МУЛЬТИПЛЕТОВ. ЭЛЕКТРОСТАТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ
- 10. ТЕОРИЯ МУЛЬТИПЛЕТОВ. МАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ
- 11. МОЛЕКУЛЫ
- 12. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ ИЗЛУЧЕНИЯ
- 13. ИНТЕНСИВНОСТЬ ИЗЛУЧЕНИЯ
- 14. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
- 15. СТОЛКНОВЕНИЯ АТОМОВ С ЗАРЯЖЕННЫМИ ЧАСТИЦАМИ
- Часть II. РЕЛЯТИВИСТСКИЕ ТЕОРИИ
- 16. УРАВНЕНИЕ КЛЕЙНА—ГОРДОНА
- 17. УРАВНЕНИЕ ДИРАКА. ФОРМАЛЬНАЯ ТЕОРИЯ
- 18. РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА
- Часть III. ВВЕДЕНИЕ В ТЕОРИЮ ПОЛЯ
- 19. КВАНТОВАНИЕ ПОЛЯ
- 20. ВТОРИЧНОЕ КВАНТОВАНИЕ НЕСКОЛЬКИХ ПОЛЕЙ ЧАСТИЦ
- 21. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ. КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- ЛИТЕРАТУРА