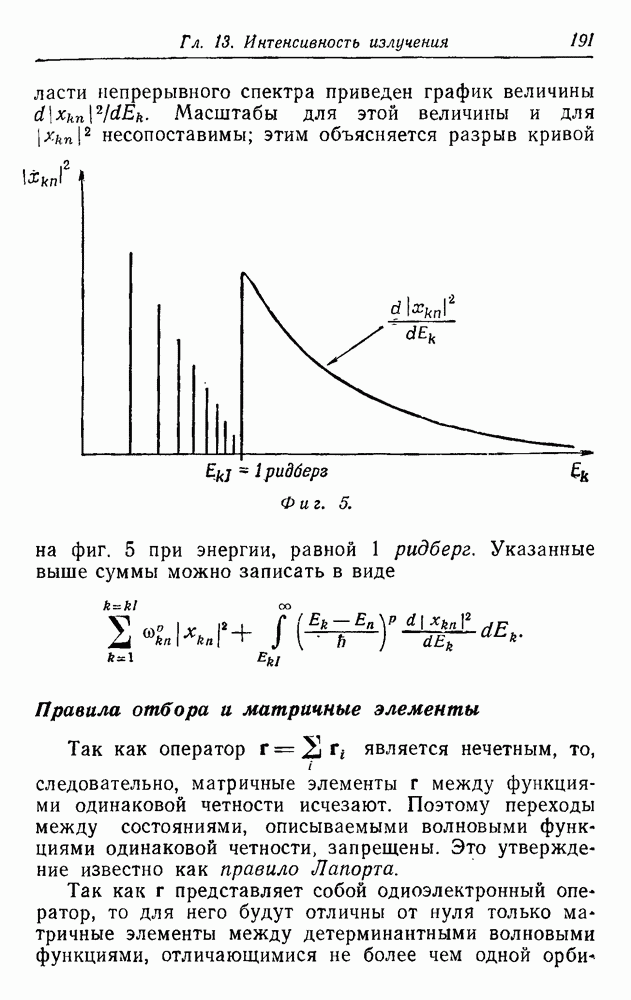
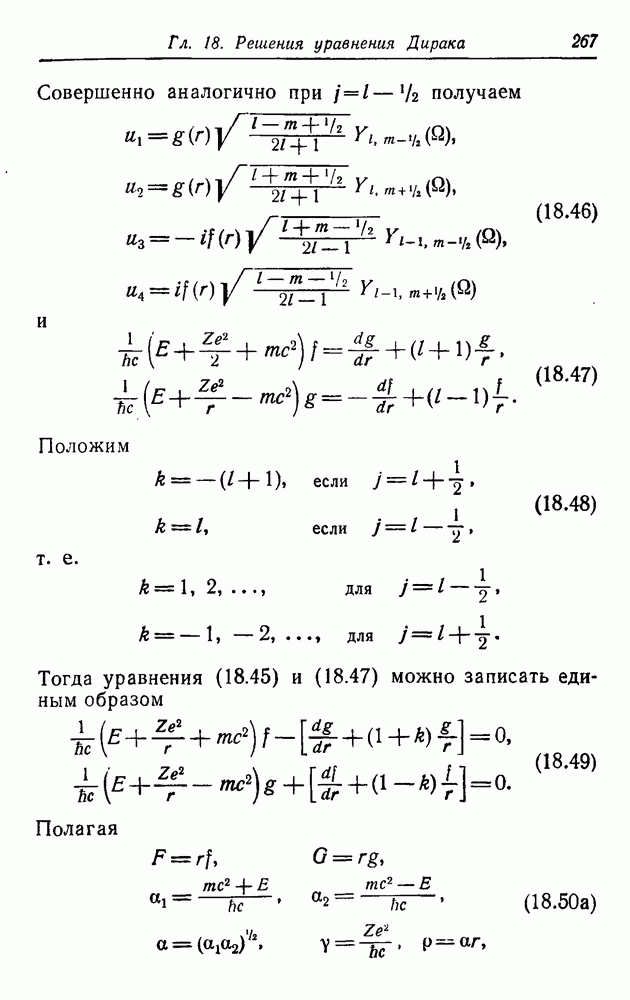| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Часть I. ТЕОРИЯ СТРОЕНИЯ АТОМА
Существуют по крайней мере три важных соображения в пользу тщательного изучения строения атомов. Прежде всего квантовая механика позволяет объяснить любую известную нам особенность электронной структуры атомов. Знание этой структуры важно для химии, физики твердого тела, спектроскопического определения свойств ядер (сверхтонкая структура и т. д.) и для многих других применений. Количественная точность теории ограничена здесь лишь вычислительными трудностями. Во-вторых, превосходное согласие теории с опытом в необычайно широком диапазоне атомных явлений дает решающую проверку справедливости квантовой механики. Наконец, теория строения атома представляет собой «теоретическую лабораторию», в которой можно познакомиться со многими физическими идеями и математическими приемами, пригодными и в других областях физики. Некоторые аспекты теории атомного ядра, например, вполне аналогичны теории атома.
1. УРАВНЕНИЕ ШРЕДИНГЕРА И ПРИБЛИЖЕННЫЕ МЕТОДЫ ЕГО РЕШЕНИЯ
Исходным пунктом нерелятивистской квантовой теории атома с зарядом ядра 1е является уравнение Шредингера

Пусть гамильтониан не зависит от времени; тогда можно обычным образом отделить переменную t, полагая

Здесь Е — полная энергия электронов. Если мы пренебрегаем всеми спиновыми взаимодействиями электронов и всеми ядерными эффектами (например, конечностью размеров и массы ядра), то уравнение (1.3) имеет вид

Здесь  есть масса электрона,
есть масса электрона,  — его заряд,
— его заряд,  - абсолютная величина радиус-вектора
- абсолютная величина радиус-вектора  электрона,
электрона,  Суммирование в первом и третьем слагаемых ведется по всем N электронам. В последнем слагаемом суммирование идет по всем парам
Суммирование в первом и третьем слагаемых ведется по всем N электронам. В последнем слагаемом суммирование идет по всем парам  причем каждая пара встречается однократно, т. е.
причем каждая пара встречается однократно, т. е.

Первое слагаемое в уравнении (1.4) описывает кинетическую энергию электронов; третье слагаемое — кулоновское взаимодействие электронов с ядром; последнее слагаемое — кулоновское взаимодействие электронов Друг с другом.
Для одного электрона уравнение (1.4) можно решить точно. Решение описывается тремя квантовыми числами  , называемыми соответственно главным, азимутальным и магнитным квантовыми числами [7]. Для большего числа электронов точные решения уравнения (1.4) не найдены. Для двух электронов существуют весьма точные приближенные методы; для многоэлектронных систем есть лишь заметно менее точные методы расчета.
, называемыми соответственно главным, азимутальным и магнитным квантовыми числами [7]. Для большего числа электронов точные решения уравнения (1.4) не найдены. Для двух электронов существуют весьма точные приближенные методы; для многоэлектронных систем есть лишь заметно менее точные методы расчета.
Методы теории возмущений
Для приближенного рассмотрения нам потребуется теория возмущений. Ниже излагаются основные результаты ее для связанных состояний. Пусть при решении уравнения (1.3) оказалось возможным представить гамильтониан в виде

где влияние оператора  мало и
мало и  . Иными словами, мы предполагаем, что невозмущенная система находится в определенном состоянии
. Иными словами, мы предполагаем, что невозмущенная система находится в определенном состоянии  с энергией
с энергией  а влияние возмущения
а влияние возмущения  таково, что Е гораздо ближе к
таково, что Е гораздо ближе к  чем к
чем к  .
.
Если собственное значение  не вырождено, то мы можем написать
не вырождено, то мы можем написать

Штрих у знака суммы означает, что слагаемое с  опущено. Если невозмущенное состояние вырождено, то необходимо найти правильную линейную комбинацию невозмущенных собственных функций, такую,
опущено. Если невозмущенное состояние вырождено, то необходимо найти правильную линейную комбинацию невозмущенных собственных функций, такую,
чтобы матрица гамильтониана возмущения была диагональна [1].
В нестационарной теории возмущений уравнение

заменяется системой

При этом

Система уравнений (1.6 а) (содержащая все коэффициенты  ) полностью эквивалентна уравнению (1.1). Ее можно решать последовательными приближениями, т. е. подстановкой выражения
) полностью эквивалентна уравнению (1.1). Ее можно решать последовательными приближениями, т. е. подстановкой выражения

с последующим приравниванием членов с одинаковыми степенями к. Если предположить, что в начальный момент система находилась в состоянии т., то мы получим

Пусть гамильтониан  не зависит от времени (не считая «включения» и «выключения» в моменты 0 и
не зависит от времени (не считая «включения» и «выключения» в моменты 0 и  ). Тогда
). Тогда

Выражение (1.96) дает (в первом приближении) вероятность перехода из состояния  в состояние
в состояние  . Таким образом, вероятность перехода в единицу времени будет
. Таким образом, вероятность перехода в единицу времени будет
 (1.10 а)
(1.10 а)
В пределе при  множитель в круглых скобках представляет не что иное, как
множитель в круглых скобках представляет не что иное, как  -функцию Дирака. (Мы предполагаем, что возмущающий гамильтониан «включен» в течение достаточно продолжительного периода времени так, чтобы оба состояния k и
-функцию Дирака. (Мы предполагаем, что возмущающий гамильтониан «включен» в течение достаточно продолжительного периода времени так, чтобы оба состояния k и  можно было считать заданными без какой-либо неопределенности.)
можно было считать заданными без какой-либо неопределенности.)
Соответственно предыдущее соотношение можно переписать в виде
 (1.106)
(1.106)
Эти выражения ясно демонстрируют тот факт, что при переходах первого порядка энергия сохраняется. Если переход происходит в непрерывный (или квазинепрерывный) спектр вблизи состояния К то следует ввести плотность конечных состояний  При этом
При этом  -функция заменяется плотностью состояний, и мы получаем хорошо известное золотое правило Ферми
-функция заменяется плотностью состояний, и мы получаем хорошо известное золотое правило Ферми

Вариационные методы
Вариационный принцип состоит в том, что функция  выбирается из условия стационарности величины
выбирается из условия стационарности величины  . При этом варьирование производится любым способом, подчиненным условию
. При этом варьирование производится любым способом, подчиненным условию  . Такой подход находит весьма разнообразные применения, которые можно классифицировать по виду применяемой пробной функции и способу ее варьирования. Один крайний случай
. Такой подход находит весьма разнообразные применения, которые можно классифицировать по виду применяемой пробной функции и способу ее варьирования. Один крайний случай
состоит в произвольном выборе пробной функции. Тогда вариация приводит нас к уравнению Шредингера

Дополнительное условие нормировки учитывается с помощью множителя Лагранжа Е, т. е. мы получаем

В последнем уравнении (1.13) использовано свойство эрмитовости оператора  . Считая вариации
. Считая вариации  и произвольными и независимыми, получаем
и произвольными и независимыми, получаем

В другом крайнем случае берется некоторая заданная пробная функция с несколькими параметрами и варьируются эти параметры. Это есть не что иное, как метод Ритца. Всякий раз, когда применяется специальный вид пробной функции или частный метод варьирования, стационарное значение  уже не является точным собственным значением гамильтониана
уже не является точным собственным значением гамильтониана  . Следующая ниже система уравнений показывает, что вариационная оценка
. Следующая ниже система уравнений показывает, что вариационная оценка  всегда дает верхнюю границу для наинизшего собственного значения энергии:
всегда дает верхнюю границу для наинизшего собственного значения энергии:
 (1.15 а)
(1.15 а)
Здесь  энергия основного состояния. Следовательно,
энергия основного состояния. Следовательно,
 (1.156)
(1.156)
Можно получить также верхние границы и для энергии возбужденного уровня, если пробная функция ортогональна ко всем собственным функциям более низких состояний.
Мы будем пользоваться в дальнейшем методом Ритца так же, как и другими более общими вариационными методами.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- Часть I. ТЕОРИЯ СТРОЕНИЯ АТОМА
- 1. УРАВНЕНИЕ ШРЕДИНГЕРА И ПРИБЛИЖЕННЫЕ МЕТОДЫ ЕГО РЕШЕНИЯ
- 2. ИНТЕГРАЛЫ ДВИЖЕНИЯ
- 3. ТОЖДЕСТВЕННОСТЬ ЧАСТИЦ И СИММЕТРИЯ
- 4. ДВУХЭЛЕКТРОННЫЕ АТОМЫ. РАСЧЕТ ПО ТЕОРИИ ВОЗМУЩЕНИЙ
- 5. ДВУХЭЛЕКТРОННЫЕ АТОМЫ. РАСЧЕТ ВАРИАЦИОННЫМ МЕТОДОМ
- 6. САМОСОГЛАСОВАННОЕ ПОЛЕ
- 7. СТАТИСТИЧЕСКАЯ МОДЕЛЬ ТОМАСА—ФЕРМИ
- 8. ТЕОРИЯ МУЛЬТИПЛЕТОВ. СЛОЖЕНИЕ МОМЕНТОВ
- 9. ТЕОРИЯ МУЛЬТИПЛЕТОВ. ЭЛЕКТРОСТАТИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ
- 10. ТЕОРИЯ МУЛЬТИПЛЕТОВ. МАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ
- 11. МОЛЕКУЛЫ
- 12. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ ИЗЛУЧЕНИЯ
- 13. ИНТЕНСИВНОСТЬ ИЗЛУЧЕНИЯ
- 14. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
- 15. СТОЛКНОВЕНИЯ АТОМОВ С ЗАРЯЖЕННЫМИ ЧАСТИЦАМИ
- Часть II. РЕЛЯТИВИСТСКИЕ ТЕОРИИ
- 16. УРАВНЕНИЕ КЛЕЙНА—ГОРДОНА
- 17. УРАВНЕНИЕ ДИРАКА. ФОРМАЛЬНАЯ ТЕОРИЯ
- 18. РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА
- Часть III. ВВЕДЕНИЕ В ТЕОРИЮ ПОЛЯ
- 19. КВАНТОВАНИЕ ПОЛЯ
- 20. ВТОРИЧНОЕ КВАНТОВАНИЕ НЕСКОЛЬКИХ ПОЛЕЙ ЧАСТИЦ
- 21. КВАНТОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ. КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА
- ЛИТЕРАТУРА